机械松动现象与故障特性研究综述

曹青松，向 琴，熊国良

（华东交通大学 机电工程学院，南昌 330013）

机械松动现象与故障特性研究综述

曹青松，向 琴，熊国良

（华东交通大学 机电工程学院，南昌 330013）

松动现象广泛存在于机械系统中，包括基础松动、支座松动及部件间配合松动。为此举例说明了三类松动的故障成因，归纳了国内外研究中常见的几种松动模型，从松动故障的动力学建模、求解方法及其非线性动力学特性等方面，对单一松动、松动—碰摩耦合、松动—裂纹耦合、两端支座松动、质量慢变系统松动与双跨转子系统松动等六类松动问题的研究现状进行了阐述，并简要介绍了松动实验的研究现状。最后，对松动故障研究中的关键问题或进一步研究课题进行了展望。

振动与波；机械松动；故障特性；转子系统；非线性振动

松动是一种常见的机械故障现象，往往是由机械安装质量不高及长期振动所引起的，其在系统基础、支承模块、内部部件及壳体等任何有连接的部位都可能发生。松动故障的存在严重影响着机械系统的正常运行，甚至导致安全事故的发生。然而，松动故障症兆通常又与不平衡、不对中等故障类似，易造成故障误判，对于耦合故障就更加难以诊断。因此，有必要对松动故障类型、松动机理、故障特征以及早期诊断进行研究。国内外学者已经针对松动现象建立了多种不同的简化松动模型，并且针对不同工作状态、不同松动情况下的系统动力学特性进行了较为的广泛研究。

在上述研究背景的基础上，本文拟分析松动主要类型及其可能发生的故障形式，综述松动模型、故障特性及实验研究等内容，并对松动故障及其诊断的进一步研究进行展望。

1 松动类型

高金吉院士总结国内外典型故障诊断案例，将旋转机械一次故障原因分为10类45种，其中，第一类的第七种与第三类的第一到三种以及第五种均可直接导致松动故障[1]。机械松动故障形式多样，本文按故障发生位置不同将机械松动分为三类：

①基础松动：主要包括机床安装地基刚性差、垫铁松动、地脚螺栓松动以及灌浆恶化或破碎等。

其故障症兆主要表现为振动方向性比较固定，振动频谱中以工作转频占主导。此类故障在工程现场经常发生，浙江一电厂发电机组的风机轴承座螺栓选用不规范，且二次灌浆混凝土标号未达设计要求，结构松散，运行一段时间后地脚螺栓松动，导致轴承内圈与大轴胶合[2]。某煤矿用轮斗系统的回转减速机地脚螺栓紧力不足，又承受反复的大作用力冲击，导致螺栓松动，挤压螺孔，形成基孔变形，变成椭圆的基孔更不易固定，使故障恶性循环[3]。

②支座松动：包括支撑脚不等长引起的晃动、结构或轴承座裂纹、轴承座或支撑座固定螺栓未充分预紧或松动等，经常发生在长期承受扭矩的机械支承结构处。

其故障症兆主要表现为振动相位不稳定，2倍工作转频的振动幅值大于1倍工作转频振动幅值的50%[4]。用于卸煤的某型翻车机，其传动齿轮工作载荷大，且长期受交变翻转力矩作用，使得其轴承座螺栓预紧力减小，联接失效，导致松动[5]。导弹支撑座在复杂的环境激励下易发生联接螺栓松动故障，此类故障会给导弹未知的初始扰动，可能造成导弹失控[6]。

③部件间配合松动：包含轴承外圈相对于轴承衬套松动、轴承内圈相对于轴松动、轴承座中的轴承衬套松动、过大的轴承内部游隙、轴系上的转子松动等现象。

其故障症兆主要表现为趋向于在松动方向的定向振动，振动频谱中同时存在高次谐波与亚次谐波等多种复杂成分[4]。此类松动在工程应用中最为常见的是轴承跑内外圈。广州一发电厂的高压电动机滚动轴承出现了内圈甩出故障，故障原因是由于轴颈磨损造成紧配合不足，轴承运转时内圈热膨胀，随即产生松动[7]。在铁路运输中列车轴箱轴承内圈松动是最常见的故障之一，内圈与车轴轴颈的配合紧密度遭到破坏造成相对滑移，轴颈表面遭到破坏并急剧升温，甚至导致热切轴事故[8]。

2 松动模型

松动模型是用来描述机械系统松动故障现象的数学形式，最为常见的一种是一端松动的简单单圆盘Jeffcott转子模型，如图1所示，m为转子圆盘等效集中质量，k为弹性轴刚度，c为圆盘处阻尼系数，e为圆盘偏心距，2α为松动间隙。系统的运动微分方程为

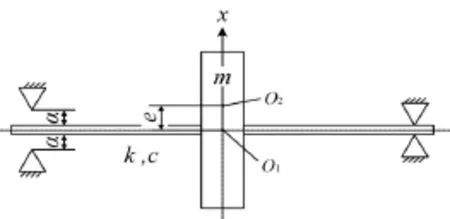
图1 Jeffcott转子系统松动简图

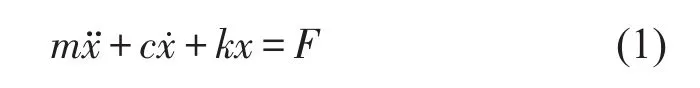
其中

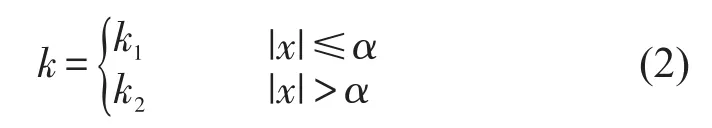
式中k1为轴端振动小于松动间隙时的系统刚度，k2为轴端振动大于松动间隙，发生机械碰撞时的系统刚度，F为系统振动外扰激励力。

随着研究的深入，式(1)已无法满足复杂工程应用的需求，对于多自由度、慢变转子质量以及不同支承形式的转子系统，需要建立能够更为准确地描述系统松动机理的模型。国内外学者通过分析各系统中m，c，k，F等参数的物理意义，建立了多种改进的松动模型。

2.1 多自由度系统松动模型

式(1)为单自由度系统振动方程，仅考虑了松动故障时转子系统竖直方向上的振动。另一种常见的松动模型如图2所示，系统一端支座松动，考虑转子m在x和y两个方向、松动支座M在y方向的振动位移，以及各部件间的相对位移与作用力，建立出多自由度的系统运动微分方程组。

图2 转子系统支座松动简图

2.2 质量慢变系统松动模型

一般情况下，转子质量m是一个恒定值，但对于离心机、翻斗机等类型的转子系统，由于物料分离，导致转子质量产生慢变，其慢变速度远小于转子的振动频率，假设物料分离过程是连续的，可采用余弦规律来描述慢变转子质量m(τ)

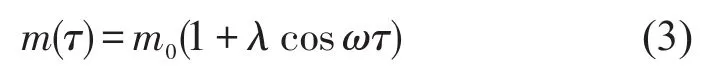
式中m0为转鼓质量，λ为质量变化幅值系数，ω为转子角速度，τ=εt(ε＜＜1)为慢变时间，ε为慢变时间系数。

2.3 连续刚度松动模型

式(2)为分段线性刚度松动模型，考虑系统振动与基座撞击产生的刚度突变，此模型较为理想化。实际情况下，松动刚度并非瞬时阶跃变化，而是随振动幅值变化的非线性连续刚度，但此复杂机理尚未明晰，仅有少数研究者建立了简单的连续松动模型

式中k1为基座刚度系数，k0为轴的刚度系数。

另有学者[9]考虑含松动故障的刚度慢变系统，此类系统具有参数慢变的特征，即系统的刚度随着时间推移存在微小慢变，而松动也会引起刚度变化，则系统总刚度的变化同时依赖于其本身慢变特征和松动现象的共同作用

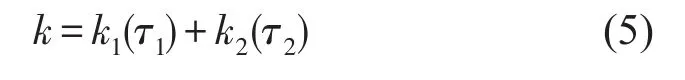
式中k1(τ1)为系统本身的刚度慢变，k2(τ2)为松动引起的系统刚度慢变，τ1=ε1t、τ2=ε2t为慢变时间，t为时间，ε1、ε2为慢变时间系数(ε1,ε2＜＜1)。

上述两种模型较分段线性刚度模型虽有所改进，但仍与实际松动现象相差甚远，松动刚度模型还需进一步研究。松动阻尼的变化规律与松动刚度基本一致，其数学模型相类似，在此不赘述。

2.4 典型对象松动模型

针对不同的研究对象，在建立动力学模型时所需考虑的受力有所差别，目前有以下几种典型对象的松动模型。

1)两端支承为滑动轴承系统的松动模型[10]。建立运动微分方程时主要考虑其作用于轴上的油膜力，油膜力的大小取决于轴承半径、轴承长度及润滑油粘度等系统特性参数。

2)两端支承为滚动轴承系统的松动模型[11,12]。与1）的区别在于支承系统的外扰激励力为滚动轴承对轴的弹性支承力，可根据非线性Hertz理论求得，由轴承类型、滚珠与滚道的接触变形量决定。

3)立式转子系统上、下导轴承松动模型，如水轮发电机组[13]。立式结构与卧式机组在分析受力时有较大差别，由于是直立布置，导轴承对轴颈没有径向静负荷，同时，需考虑止推轴承对的轴向作用，转—定子轴向错位产生的轴向磁拉力等。

4)双跨转子系统松动模型[14]。相对于单跨转子系统具有更多自由度，建模时需考虑两转子系统间的相互作用。

5)松动与其他故障耦合模型。主要有松动—碰摩耦合、松动—裂纹耦合等故障模型，建模时需分别考虑碰摩力、裂纹开闭等作用因素。

3 几种典型的松动故障研究

松动故障的研究是为了切合实际地描述出系统在松动故障下的量变与质变过程，实现系统的早期故障诊断，预防事故发生。国内外学者已就单一松动、松动—碰摩耦合、松动—裂纹耦合、两端支座松动、质量慢变系统松动以及双跨转子系统松动等六种典型故障进行了较为广泛的研究。

3.1 单一松动故障

褚福磊等[15]研究了一端支座松动的转子—滑动轴承系统，采用分段线性刚度和阻尼的松动模型，通过数值仿真发现这类系统具有多种形式的周期、拟周期和混沌的复杂运动特性，还运用打靶法求出系统的振动周期解，并结合Floquet理论对解的稳定性进行了判定。考虑到转子系统中转轴的应力应变关系通常为非线性函数关系，李宏坤等[16]建立转子—滑动轴承动力学模型时，以线性项和立方项之和来表示转轴的非线性弹性力，区别于普遍采用的线性弹性力。刘献栋等[11]以转子动力学、Hertz接触理论和非线性动力学理论为基础，建立了转子—滚动轴承系统支承松动故障动力学模型，分别利用Fourier变换和小波变换进行信号处理，不仅获得了转子—滚动轴承系统的松动故障特性，还证实了小波变换在松动故障诊断中的优越性。陈果[12]建立了含支座松动故障的转子—滚动轴承—机匣耦合系统动力学模型，通过数值仿真获取了不同转速、不平衡量、轴承座质量以及支承刚度下的系统响应，发现在较大不平衡量和较小轴承座质量下甚至出现超临界转速区域比临界转速区域更大的振动，较低机匣—基础之间和轴承座—机匣的之间的连接刚度能够降低系统响应振幅。马辉等[17]采用有限元法对工程中常见的一类轴承盖松动故障建立了系统松动模型，并利用Ansys软件进行仿真分析，得出轴承盖松动故障的振动特性。Xiong等[18]针对含支承松动的偏心电机转子系统开展研究，采用增量谐波平衡法对分段线性的松动模型进行求解，获得了系统的近似周期解，并仿真分析了系统的故障特性。

由此可知，系统存在单一松动故障时的动力学特性研究已渐成体系，已从相对简单的转子—滑动轴承系统着手，一直发展到复杂的转子—滚动轴承—机匣耦合系统，通过对系统进行动力学建模，采用Runge-Kutta法、Newmark-β法、打靶法、渐进法和增量谐波平衡法等数值方法进行求解，分析系统的松动故障特性。

3.2 松动—碰摩耦合故障

转子碰摩是旋转机械的常见故障，即转子与定子间的碰撞与摩擦。目前对于碰摩故障的研究较多，从简单的单圆盘转子模型静碰摩机理的研究[19，20]，到多圆盘转子系统非线性动力学特性[21]与整周碰摩模拟实验的研究[22]，再到转子系统反向全周碰摩的研究[23]，碰摩故障理论已发展得较为深入。

碰摩故障使得旋转机械受到周期性冲击，诱发松动；而松动故障引起系统的周期性跳动，亦会导致碰摩。因此实际的转子系统极可能同时具有松动与碰摩两类故障，松动—碰摩耦合故障的特性研究十分必要。Muszynska与Goldman关于旋转机械系统的动力学特性研究做了大量工作[24-26]，对松动与碰摩耦合故障的横向不平衡转子系统进行了数值仿真，并利用转子实验台对仿真结果进行了实验验证[27]。刘元峰等[28]以具有支承松动的Jeffcott转子为研究对象，综合考虑转子系统的碰摩故障与基础松动，创建了既包含碰摩力，又存在分段阶跃刚度的转子系统振动微分方程，并采用数值方法分析系统的分岔与混沌等非线性动力学特性。在此基础上，罗跃纲等[29]研究了结构相对复杂的转子系统，建立了多自由度的运动微分方程组，通过连续打靶法求出了非线性非自治系统的周期解，利用Floquet理论分析系统周期运动的稳定性及不稳定规律。除常见的卧式机构外，黄志伟等[13]研究了立式机组—水轮发电机组轴系松动—碰摩耦合故障的动态响应，建立了上导轴承松动与转子碰摩耦合故障情况下，具有六自由度的水轮发电机组轴系动力学模型。

大多数相关研究在分别考虑转子系统碰摩、松动二者故障机理的基础上，建立松动—碰摩耦合故障模型，通过改变系统频率比、松动质量、偏心量等参数来观察系统松动—碰摩耦合故障特性。现有研究结果表明相对于单一松动故障，松动—碰摩耦合故障的系统响应具有更丰富的低频谐波分量。

3.3 松动—裂纹耦合故障

旋转机械转轴上出现裂纹，导致转轴刚度的时变与不对称，从而引发一系列复杂的动力学行为，裂纹转子模型主要有两类，假设转轴刚度为随裂纹开闭按余弦函数规则变化的方波模型，及考虑轴刚度、裂纹开闭和转轴位移三者耦合的非线性涡动模型。Yang等[30]采用适当的裂纹开闭模型，导出固定坐标系中裂纹轴的刚度矩阵，研究了裂纹转子的动力学特性。Mohiuddin等[31]建立了裂纹转子—轴承系统的有限元模型，并对光轴、锥形轴以及阶梯轴三种不同情况进行了实例仿真。陈铁锋等[32]运用有限元方法对具有两条横向裂纹的转子系统动力学特性进行仿真分析，研究了不同裂纹夹角的转子动力学行为。

当已存在裂纹的系统出现松动故障时，其动力学行为将变得十分复杂。李振平等[33]基于裂纹转子系统的数学模型，考虑支承松动故障，建立了松动—裂纹耦合故障转子系统的运动微分方程，应用龙格库塔法仿真分析了该转子系统的耦合故障特性。杨永锋等[34]在李振平等人研究的基础上，采用Newmark-β法对小裂纹情况下，松动—横向刚度—副裂纹方向刚度共同作用下的耦合故障转子系统进行了数值模拟研究。刘长利等[35]利用了延拓打靶方法求解松动裂纹耦合故障转子轴承系统的非线性动力学方程，研究了系统响应的分岔及稳定性。

裂纹故障使得转子系统发生拟周期运动，松动故障使得转子系统发生混沌运动，同时存在松动与裂纹故障时，松动故障将占主导地位，随着裂纹深度增加，其影响作用逐渐增大。

3.4 两端支座松动故障

对于支承松动故障的研究大多仅限于一端支座发生松动的情况，实际上，由于机械系统长期处于振动状态，导致多个支座都可能发生不同程度的松动，因此，研究转子轴承系统中两端支座与基础之间同时出现松动故障时系统的非线性特性是有必要的。张靖等[36]应用现代非线性动力学理论，采用成熟的非稳态非线性油膜力模型，建立了带有两端支座松动故障的转子—轴承系统的非线性运动微分方程。马辉等[37]针对工程中出现的支座松动故障，建立了多盘悬臂转子的松动有限元模型，对单支座和双支座松动两类故障情况分别进行了动力学特性研究。

带有两端支座松动故障的转子—轴承系统运动在未到共振区时以周期运动为主，在过共振区后，运动形式以拟周期和混沌为主，两个松动支座的振动在一定程度上相互抑制。

3.5 质量慢变系统松动故障

离心机是一种应用十分广泛的高速旋转机械，其显著特点是转子质量在系统运转过程中会发生慢变，从而导致此类转子系统具有不同于恒定质量转子系统的动力学特性。王宗勇等[38]分析了转子质量慢变规律，建立了带有支承松动故障的质量慢变转子系统的动力学模型，利用数值积分法对该转子系统由于支承松动故障而导致的动力学行为进行了仿真研究。还研究了带支承松动故障的质量慢变—滚动轴承系统，除质量慢变因素外，还考虑了滚动轴承的支承反力，建立了带一端支座松动故障的滚动轴承质量慢变转子系统的非线性动力学模型。考虑慢变转子系统存在碰摩故障的情况，建立了带支承松动—碰摩耦合故障质量慢变转子系统的动力学模型，分析了质量慢变时间系数对转子系统动力学行为的影响[39]。

通常，质量慢变系统的慢变时间系数对转子系统的混沌运动有较大影响，随着慢变时间系数的增大，转子系统响应产生混沌运动的频率范围扩大，近拟周期运动区间减小，转子响应的波动范围逐渐增大，可见，慢变时间系数的增加会促进混沌运动的发生。

3.6 双跨转子系统松动故障

关于松动故障研究的对象大多为单跨转子系统，但工程上许多大型转子系统却是由多跨转子组成。罗跃纲等[40]建立了含有支承松动故障的三轴承支承双跨弹性转子—轴承系统非线性动力学模型，分析了松动质量对系统非线性特性的影响，采用延拓打靶法和Floquet理论研究了系统周期运动的稳定性及失稳规律；再考虑双跨转子系统基础松动—碰摩耦合故障的情况，建立三轴承支承的双跨弹性转子系统松动—碰摩耦合故障的动力学模型，分析了耦合故障特性与单一故障特性的区别[14,41]。除此之外，卢艳军等[42]通过建立松动—碰摩耦合故障的双盘悬臂立式转子—轴承系统的力学模型及有限元模型，基于接触理论研究了松动刚度及碰摩间隙对系统动力学特性的影响。刘杨等[43]利用有限单元法建立了一个三支撑的松动-碰摩耦合故障双盘转子轴承系统模型，采用数值积分法分析了中间轴承松动-碰摩耦合转子轴承系统在不同碰摩刚度、松动刚度参数域内系统的动力学特性，得到该转子系统松动-碰摩耦合的主要故障特征。

双跨转子系统与单跨转子系统相比，机械部件繁多，各部件间相互作用，使得系统动力学模型更加复杂，故障特性常表现为在不同转速下，系统以不同分岔形式失稳。

4 松动故障的实验研究

上述关于松动故障特性的研究均采用动力学建模结合数值求解的方法，而早在1996年，徐煜兵等[44]就已通过对转子系统轴承座地脚螺钉紧力不足以及轴承间隙变大两种典型松动故障的情况进行了实验，测取轴承的振动信号，归纳出系统存在此两类故障时的故障症兆，为滑动轴承松动的故障诊断提供了可信的故障信息。马辉等[45]在进行动力学建模研究转子系统松动故障特性的同时，也进行了旋转机械支座松动故障实验，并利用三维谱阵图、小波尺度图和轴心轨迹图对采集到的振动信号进行分析处理。董广明等[46]针对某导弹支撑座在环境激励下易引发连接螺栓松动这一具体问题，在支撑座包带与其槽形支撑的12个连接螺栓紧固和松动的不同情况下，检测支撑座在垂向宽带随机激励下的动态响应。曲秀秀等[47]采用ZT-3型多功能转子模拟实验台进行了转子系统不平衡、基座松动与转静碰摩等实验，验证了其建立的不平衡—碰摩—基础松动耦合故障转子动力学模型的正确性。Lu等[48]利用转子轴承系统实验装置研究带松动故障时系统的振动特性，通过改变转速、松动间隙、不平衡质量及转盘位置等参数来观察系统的非线性振动特性。张颖等[49]在600 MW模化汽轮机转子试验台上进行了转子正常运转、转子不平衡故障、转子不对中故障、汽流激振故障、轴承松动故障的实验研究，将获得的振动参数三维图形转化为二维灰度图形，对二维灰度图形进行模糊软形态学滤波增强处理和自适应边缘检测，提取到了转子系统不同状态下振动参数图形的边缘特征。

松动故障试验台一般由电机、转轴、轴承、轴承座、基座、转子及振动传感器等核心部件组成，目前已有的试验方法大都通过拧松轴承座或基座的紧固螺栓来模拟松动现象，采用加速度传感器采集检测节点振动信号，通过快速傅里叶变换（FFT）、希尔伯特-黄变换（HHT）、小波分析、包络分析、形态运算等方法进行故障特征提取，为松动的故障诊断提供依据。

5 研究展望

基于动力学模型与实验方法的松动故障特性研究已取得较大进展，笔者对机械松动故障研究中的有关关键问题展望如下：

1)更为准确的松动模型及有效的求解方法。

实际的松动现象是由隐形到显形，失效渐变过程复杂，且表现形式多样，如螺栓预紧力下降，焊接裂纹萌生，过盈配合量减小等，故应采用非线性连续模型来描述实际松动故障，并以此建立出更为准确的松动模型。松动模型的求解大多采用数值积分方法，仅能分析系统的典型故障特征，无法获得振动响应解析解，而解析解却能更好的解释松动故障机理。已用于松动问题求解析解的方法有打靶法、渐进法与增量谐波平衡法，但求得的解均为近似解析解，精度不高，因此，开发能实现复杂强非线性系统求解析解的有效方法十分必要。

2)典型松动故障特性及其对比。

已有的研究大多针对特定系统分别进行单一松动故障或松动耦合故障特性研究，缺乏各故障特性的对比。进行故障诊断时，松动故障特征虽明显，却无法根据检测信号准确判别是单一故障、松动—碰摩耦合或松动—裂纹耦合故障。因此，开展松动、各松动耦合故障的故障特性对比研究至关重要。

3)新型实验方法与手段的探索。

松动研究的不同领域、不同对象使得实验设备千差万别，实验经费剧增，已有文献大都倾向于采用计算机进行松动故障的仿真研究，但仿真一般存在简化条件，离实际情况还有一定差距，无法完全替代实验研究。因此，有必要对落后的实验手段进行改进，开发经济可靠的新型实验方法，提高实验研究水平。

[1]高金吉.旋转机械振动故障原因及识别特征研究[J].振动、测试与诊断，1995，15(3)：1-8.

[2]胡建峰.引风机地脚螺栓松动后的处理[J].风机技术，1995，01：42-43.

[3]王荣钧.轮斗系统皮带车A回转减速机地脚松动故障分析[J].露天采矿技术，2012，04：70-71.

[4]赵黎辉，岳万军，李振威，等.机械松动故障的诊断[J].中国新技术新产品，2009，16：125-126.

[5]杨开国.CFH-II型翻车机传动齿轮轴承座的座脚螺栓联接失效分析与改进[J].制冷空调与电力机械，2003，03：64-67.

[6]樊战军，张高峰，江登林.某弹性支撑导弹发射装置动力学特性的研究[J].2013，33(5)：173-176+180.

[7]吴(子尽)德.J S系列高压电动机滚动轴承内圈甩出故障分析及处理[J].电机技术，2005，03：57-60.

[8]Mypaвьe B B B，宋忠明.轴承和轮轴摩擦连接处的声信号传输过程的计算[J].国外机车车辆工艺，2008，1：29-33+36.

[9]刘挺，冯霏，赵增晖，等.松动条件下刚度慢变转子的研究[J].中国工程机械学报，2011，9(2)：229-232.

[10]Gunter E J,Barrett L E,Allaire P E.Design of nonlinear squeeze-film damper for aircraft engines[J].Journal of Lubrication Technology,1977,99(1):57-64.

[11]刘献栋，何田，李其汉.支承松动的转子系统动力学模型及其故障诊断方法[J].航空动力学报，2005，20(1)：54-59.

[12]陈果.转子—滚动轴承—机匣耦合系统的不平衡松动棍合故障非线性动力学[J].机械工程学报，2008，44(3)：82-88.

[13]黄志伟，周建中，张孝远，等.水轮发电机组轴系松动-碰摩耦合故障的动态响应[J].西南交通大学学报，2011，46(1)：121-126.

[14]罗跃纲，张松鹤，闻邦椿.双跨松动—碰摩转子—轴承系统周期运动稳定性[J].机械强度，2010，32(6)：894-898.

[15]CHU F,TANG Y.Stability and non-linear responses of a rotor-bearing system with pedestal looseness[J].Journal of Sound and Vibration,2001,241(5):879-893.

[16]李宏坤，赵利华，练晓婷.非线性刚度转子—轴承支承松动故障的特征分析[J].动力学与控制学报，2011，9 (3)：233-237.

[17]MA H,ZHAO X,TENG Y,et al.Analysis of dynamic characteristics for a rotor system with pedestal looseness [J].Shock and Vibration,2011,18(1):13-27.

[18]XIONG G L,XIANG Q,CAO Q S.Bearing looseness fault characteristics analysis of rotor system based on incremental harmonic balance method[J].Applied Mechanics and Materials,2013,397:517-523.

[19]陈虹微.离心压缩机碰摩振动建模及改进方法[J].噪声与振动控制，2013，4(2)：205-210.

[20]Smalley A J.The dynamic response of rotors to rubs during startup[J].Journal of Vibration and Acoustics, 1989,111(3),226-233.

[21]YANG Y,ZHANG S,HAN Q,et al.Characteristics of variable parameters in rotor system with rub-impact fault [A].Intelligent Control and Automation of World Congress[C].IEEE,2010:5947-5952.

[22]CHEN G,LI C G,WANG D Y.Nonlinear dynamic analysis and experiment verification of rotor-ball bearings-support-stator coupling system for aero engine with rubbing coupling faults[J].Journal of Engineering for Gas Turbines and Power,2009,132(2):022501(1-9).

[23]张华彪，陈予恕.非线性转子的反向全周碰摩响应[J].振动与冲击，2013，32(10)：84-90.

[24]Goldman P,Muszynska A.Analytical and experimental simulation of loose pedestal dynamic effects on a rotating machine vibrational response[J].Rotating Machinery and Vehicle Dynamics,1991,35:11-17.

[25]Goldman P,Muszynska A.Chaotic behavior of rotor/stator systems with rubs[J].Journal of Engineering for Gas Turbines and Power,1994,116(3):692-701.

[26]Goldman P,Muszynska A.Dynamic effects in mechanical structures with gaps and impacting:order and chaos [J].Journal of Vibration and Acoustics,1994,116(4): 541-547.

[27]Muszynska A,Goldman P.Chaotic responses of unbalanced rotor/bearing/stator systems with looseness or rubs [J].Chaos,Solitons&Fractals,1995,5(9):1683-1704.

[28]刘元峰，赵玫，朱厚军.转子有碰摩和支承松动故障时的混沌特性研究[J].振动与冲击，2002，21(4)：36-38.

[29]罗跃纲，曾海泉，李振平，等.基础松动—碰摩转子系统的混沌特性研究[J].振动工程学报，2003，16(2)：184-187.

[30]YANG B,SUH C S,CHANAK.Characterization and detection of crack-induced rotary instability[J].Journal of Vibration andAcoustics,2001,124(1):40-48.[31]Mohiuddin M A,Khulief Y A.Dynamic response analysis of rotor-bearing systems with cracked shaft[J].Journal of Mechanical Design,2002,124(4):690-696.

[32]陈铁锋，荆建平，孟光，等.双裂纹转子振动特性的有限元和实验研究[J].噪声与振动控制，2010，10(5)：15-19.

[33]李振平，闻邦椿，张金换，等.松动—裂纹藕合故障转子系统的非线性动力学行为研究[J].中国机械工程，2003，14(22)：1891-1895.

[34]杨永锋，任兴民，秦卫阳.松动—裂纹耦合故障转子系统的非线性响应[J].机械科学与技术，2005，24(8)：985-987.

[35]刘长利，郑建荣，周炜，等.松动裂纹转子轴承系统周期运动分岔及稳定性分析[J].振动与冲击，2007，26(11)：13-15.

[36]张靖，闻邦椿.两端支座松动转子系统的频率特性分析[J].中国机械工程，2008，19(1)：68-71.

[37]马辉，孙伟，任朝晖，等.多盘悬臂转子系统支承松动故障研究[J].航空动力学报，2009，24(7)：1512-1517.

[38]王宗勇，吴敬东，闻邦椿.支承松动的质量慢变转子系统混沌特性研究[J].中国机械工程，2005，16(2)：165-168.

[39]王宗勇，吴敬东，闻邦椿.质量慢变转子系统的松动与碰摩故障研究[J].振动工程学报，2005，18(2)：167-171.

[40]罗跃纲，闻邦椿.双跨松动转子—轴承系统周期运动稳定性[J].振动与冲击，2007，26(8)：9-12.

[41]罗跃纲，杜元虎，任朝晖，等.双跨转子—轴承系统松动—碰摩耦合故障的非线性特性[J].农业机械学报，2008，39(11)：180-183.

[42]卢艳军，任朝晖，陈宏，等.双盘悬臂转子轴承系统松动碰摩耦合故障分析[J].振动、测试与诊断，2007，27(2)：102-107.

[43]刘杨，太兴宇，马辉，等.双盘三支撑转子轴承系统松动－碰摩耦合故障分析[J].航空动力学报，2013，28(5)：977-982.

[44]徐煜兵，黄树红，贺国强，等.测取滑动轴承松动故障信息的研究[J].振动与冲击，1996，15(4)：18-20.

[45]马辉，孙伟，刘杰，等.旋转机械支座松动故障的实验[J].农业机械学报，2007，38(6)：134-137.

[46]董广明，陈进，雷宣扬，等.导弹支撑座连接螺栓松动故障诊断的实验研究[J].振动、测试与诊断，2005，25(3)：174-178.

[47]曲秀秀，陈果，乔保栋.不平衡—碰摩—松动耦合故障的转子动力学建模与盲分离研究[J].振动与冲击，2011,30(6):74-77+96.

[48]LU W X,CHU F l.Experimental investigation of pedestal looseness in a rotor-bearing system[J].Key Engineering Materials,2009,413:599-605.

[49]张颖，苏宪章，刘占生，等.旋转机械参数图形软形态学自适应边缘检测[J].哈尔滨工业大学学报，2012，44(3)：49-53.

Review of Mechanical Looseness Phenomena and Failure Characteristics Study

CAO Qing-song,XIANG Qin,XIONG Guo-liang
(School of Mechanical and Electrical Engineering,East China Jiaotong University, Nanchang 330013,China)

There exist looseness phenomena in mechanical systems,including foundation looseness,pedestal looseness and component match looseness.The causes of the three types of looseness were explained with examples.Some common types of looseness models were summarized.Research status of six types of looseness,including single looseness,looseness coupled with rub-impact,looseness coupled with crack,looseness at two end-supports,looseness of rotor system with slowly varying mass,and looseness of double-span rotor system was elaborated in the aspects of dynamics modeling,solution method and their nonlinear dynamic characteristics.Research of looseness experiments were also introduced briefly.Finally,the hot points for further study of the looseness faults were prospected.

vibration and wave;mechanical looseness;failure characteristics;rotor system;nonlinear vibration

2；TH113

A

10.3969/j.issn.1006-1335.2015.02.001

1006-1355(2015)02-0001-06+23

2014－09－13

国家自然科学基金（51265010）；华东交通大学研究生创新专项资金项目（YC2013-X007）

曹青松（1978－），男，安徽无为人，博士，副教授，研究方向：无损检测、机电一体化以及振动控制。E-mail:2000cqs@163.com