流体激励诱发轴流泵结构振动计算方法

赵 博，陈长盛，符栋梁，王 强

(1.海军驻上海704所军事代表室，上海 200031 2.中船重工第七〇四研究所，上海 200031)

流体激励诱发轴流泵结构振动计算方法

赵 博1，陈长盛2，符栋梁2，王 强2

(1.海军驻上海704所军事代表室，上海 200031 2.中船重工第七〇四研究所，上海 200031)

泵内非定常压力脉动会引发泵体的结构振动，而由压力脉动引发结构振动的计算方法是一个值得研究的问题。通过有限元分析软件对某台立式轴流泵内流体压力脉动引发的结构振动响应进行了仿真计算。将数据处理后与试验值进行了对比，并对该方法准确性和可行性进行了分析。结果表明：该计算方法可以用于已知压力脉动情况下叶频振动加速度的预估，若增加采样点个数，采样频率提高，可以提高叶频高次谐波频率的识别能力。

振动与波；轴流泵；压力脉动；结构振动；瞬态分析

文献[3]中建立了某船用泵的有限元模型，进行了振动模态的计算分析，并给出了泵的性能评价，但是并未计算对流体激励的振动响应；文献[4]首先对某离心泵内部三维流动进行了计算，并求得了在集中径向力激励下蜗壳的振动响应，但是建模时未将电机考虑在模型内，且计算中设置进出口法兰为自由边界条件，结果有较大偏差；文献[5]利用网格对应方法，编制了程序将流体计算网格和固体界面网格进行对应，并将蜗壳所受的流体脉动压力作为激励进行输入，以计算泵体的振动响应。

从以上文献中可知，目前国内外对泵组振动计算研究主要使用混合数值计算法，即先计算流场流动特性，在得到流体激励力特性之后，再对泵组结构进行振动响应计算。但是大部分研究均只考虑蜗壳壁面的流体激励力，而叶轮表面所受脉动压力未予考虑。

本文以一台轴流泵为研究对象（如图1所示），建立了全三维实体模型，应用瞬态响应分析法对流体激励引发的结构振动进行了计算分析。

1 瞬态响应分析基础

瞬态动力学方法是一种在时变载荷的激励下，研究结构动力学响应过程的时域分析技术。瞬态动力学分析中所施加的载荷是时间的函数，而响应得到的结果同样也是随着时间变化的位移等量。

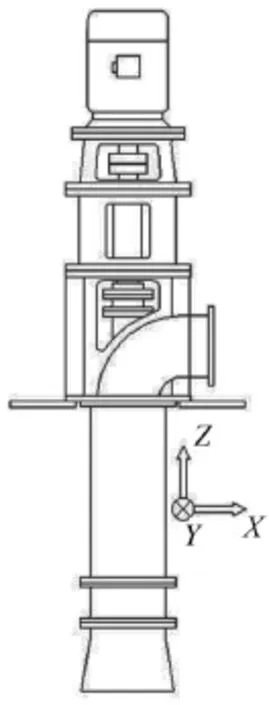
图1 轴流泵CAD总装图

瞬态动力学分析由于是时域分析，所以往往要占用较多的计算机资源。为简化计算过程和缩短计算周期，在瞬态动力学分析的初始阶段，先对一个简单的模型进行分析，若该模型中存在非线性结构，可以先进行静力学分析，以获得非线性对整个结构的影响；而在没有必要进行非线性动力分析时，可以使用模态分析的方法获得模型的固有频率和振型；对非线性问题，应考虑将模型的线性部分结构化。

瞬态动力学一般方程为

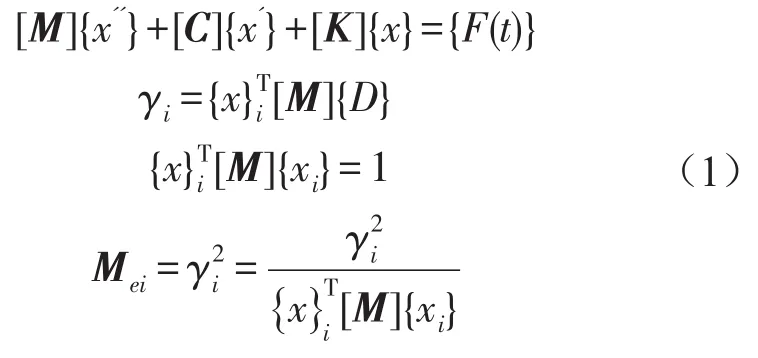
式中[M]是质量矩阵，[C]是阻尼矩阵，[K]是刚度矩阵，{x}是位移矢量，{F(t)}是力矢量，{x’}是速度矢量，{x’’}是加速度矢量。

为何过量施用钾肥会导致土壤中钙含量不足？西蒙说：“钾肥和钙肥同属于阳离子，在作物吸收过程中，钾会把大部分中微量元素的阳离子拮抗掉，钙就是其中一个。种植者大量的施用钾肥造成土壤中钾离子浓度过高，从而影响了根部钙的吸收。”对此，何金钢建议种植者在冲施利于膨果的水溶肥期隔3-4次冲施一次中微量元素。这样可以补充60%-70%钙肥及其他中微量元素，剩余30%-40%可通过叶面喷施来进行补充。这样可以保证作物需求高峰期钙肥的供应量。

2 流体激励诱发结构响应计算

2.1 非定常流体激励力计算

要研究轴流泵结构振动的计算方法，首先要取得泵内流场的非定常脉动压力[6]。本文采用大涡模型，利用Fluent对泵内流场非定常流动进行了计算，计算选取额定工况，即转速取1 450 r/min，流量为450 t/h。

在得到非稳态场计算结果后，通过选取不同点的压力脉动数值进行分析，得出远离叶轮区域的压力脉动值相比于叶轮区域内的点已经非常的小，所以在振动响应计算中的流体激励力，主要考虑作用在叶轮区域内壁面上的压力以及流体作用在叶轮表面上的力。

由于非定常流动计算量较大，而本章节只做方法性研究，故只选取4叶片叶轮的情况加以分析。计算过程中，以轴转动6°为一个时间步长，在提取流体激励力时，从转动第6圈起开始采样（此时默认为流动状态已趋于均匀稳定），采样时间为轴转动一圈，即360°，故共有60个采样点。在保存了每一步的计算结果后，由Fluent对内壁面和叶轮表面的流体脉动压力分别进行空间平均，得到作用于叶轮区域内壁面上的平均压力值以及作用在叶轮表面的力。

2.2 轴流泵振动响应计算

将轴流泵三维模型进行适当简化处理，将不影响结构特性但是会影响网格质量的如螺栓孔、凸台、肋板等结构省去，并将简化后的模型导入Ansys Workbench中的Transient Structural模块，作为计算模型。

泵组实际安装状态为底板四个角通过四个BE-300隔振器与安装基座相连，出口处通过一250 mm双球管与延伸管段连接，延伸管段马脚处与地面用螺栓拧紧，视为刚性连接。为在计算中与实际情况保持一致，在Ansys中设置底板四个角以及泵出口处为Body-Ground连接，将隔振器简化为弹簧单元，按表1中的参数设置刚度值和阻尼比；按照双球管产品手册上提供的双球挠性接头的轴向静刚度和双球挠性接头的横向静刚度曲线图分别设置双球挠性接管的横向、轴向刚度值。

表1 隔振器动刚度及阻尼比

设置完边界条件之后，对泵组进行网格划分，由于结构较为复杂，规则管段采取网格扫略，不规则部分由Ansys软件进行自由划分，为得到较为精确的结果，将网格尺寸设置较小，划分好的网格如图2所示。

在网格划分结束之后，将Fluent中采样得出的60个时间点的数据提取出来，并加载在叶轮区域内壁面和叶轮表面上。图3所示为作用于叶轮区域内壁面的流体激励力，作用方向如图中所示，可以看出，X、Y两个方向的流体作用力脉动幅度较大，而Z向的力脉动量很小；图4为作用于叶轮表面的流体激励力，从图中数据可得，作用在叶轮X和Y两向的流体激励力很小，相比之下，Z向的作用力较大，但是脉动量与作用在泵壳内壁面的力相比还是相差较多。

图2 泵组整体网格划分

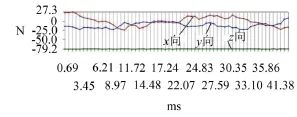
图3 作用于叶轮区域内壁面的流体激励力

图4 作用于叶轮表面的流体激励力

设置求解步数为60步，与输入作用力保持一致，时间步长0.006 9 s，60步总时间0.041 379 s，即为叶轮轴旋转一圈所用时间。设置三个输出响应点，分别位于水泵出口处、泵组底板机脚位置和泵身位置，求解三点Z向的瞬态响应。

图5标出了三个响应点在实体模型中的位置。

图5 三个输出响应点位置

运算完成之后，可以得到三个点各自的位移随时间的变化，图6为水泵出口、泵组机脚和泵身的位移—时间响应曲线。

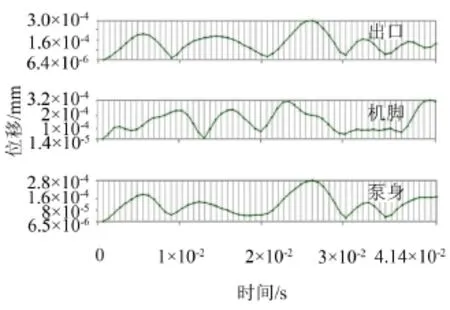
图6 水泵出口、机脚和泵身位移—时间响应曲线

3 结构振动响应信号处理

计算完成之后，用Matlab软件对所得数据进行处理，由于加速度为位移进行二次求导所得，为使求导结果更为精确，首先对60个离散时间点的位移响应进行高阶函数拟合，经过多次调试，最后综合计算机运行效率和拟合精度考虑，选取20阶拟合函数。图7给出了拟合后的曲线和拟合前的离散值对比情况，从图中可以明显看到，经过拟合，曲线已经尽可能不失真地表达出各离散点的数值。

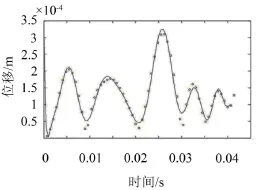
图7 20阶拟合位移—时间函数

对拟合所得的函数进行求导，则得到速度—时间曲线，如图8所示。

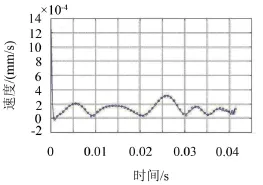
图8 速度—时间曲线

再对速度—时间函数进行求导运算，即可得到如图9的加速度随时间变化的曲线。

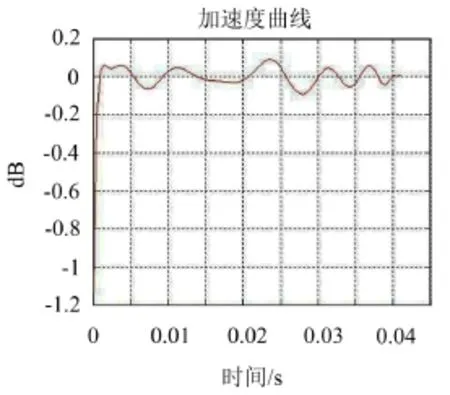
图9 加速度—时间曲线

用Matlab对加速度时域数据进行快速傅里叶变换（FFT），即可得到加速度的频率数值。再将振动加速度通过下式转换为dB单位

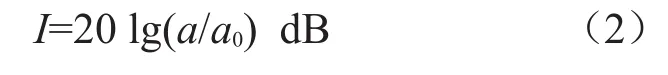
式中，参考值a0=1 um/s2。以频率为横坐标，振动加速度I为纵坐标作图，则可得到泵出口的振动加速度频谱图，如图10所示。由于采样频率较低，采样点数较少，故经过FFT之后频率分辨率间隔很大，每一频率单位相隔为24.17 Hz。从图中可以看出，有三个频率特征较为明显，即84.61 dB（24.17 Hz）的轴频，91.71 dB（96.67 Hz）的叶频，以及89.86 dB（193.33 Hz）的二倍叶频。

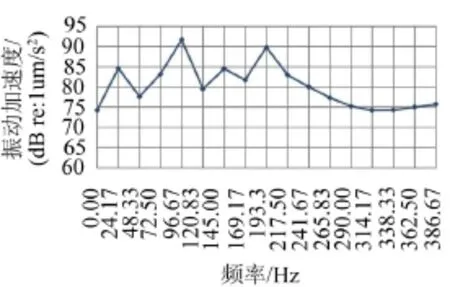
图10 泵出口振动加速度

同理，经过上述一系列的处理方式，可以得到泵身和机脚的振动加速度曲线。如图11和图12。

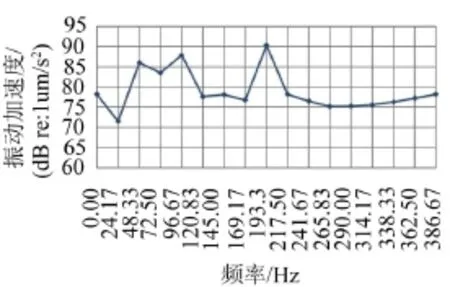
图11 泵身振动加速度

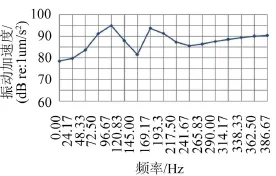
图12 机脚振动加速度

综合三张图分析可以看出，叶频（96.67 Hz）是最主要的特征频率，峰值在每个响应点都有明显体现，轴频在机脚处和泵身都未明显地体现出来，这是因为轴频由转子不平衡等原因产生，而进行流体计算时，轴系部分未考虑不平衡量，默认作均匀化处理，故激励中并无轴频成分。且由于样本数据的限制，在250 Hz以上的频率特征可识别性较差，无法再体现出特征频率峰值。

4 计算方法准确性及可行性分析

为验证该计算方法的准确性，通过实验手段测得4叶片叶轮在1 450 r/min转速下，额定流量450 t/h时的振动加速度，图13中显示了泵出口、泵身和泵组机脚振动加速度频谱。从图中可以看到，实测叶频频率值为99.61 Hz，和计算所得结果基本一致。

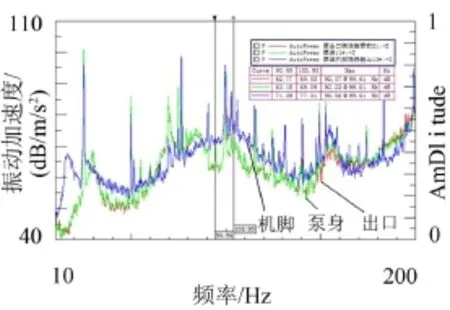
图13 叶频振动加速度测试值

将频谱中三点的叶频幅值提取列入表2中，并与计算值进行对比分析。泵出口处的叶频振动计算值与实验值最为接近，只相差0.36 dB，而泵身处的计算值与实验值则相差较大，为4.34 dB，由于泵身点选取位置位于弯管段流体转向处，内部流场流动较为复杂，流体在转弯处对泵身也会产生不稳定的脉动压力，而在计算中仅仅考虑了叶轮位置的脉动压力传递到泵身位置的振动响应；且由于泵身处机械密封等位置存在机械因素的影响，而本文只考虑在的，这导致仿真误差的出现。

Calculation Method of Structural Vibration ofAxial Flow Pumps Induced by Fluid Pressure Pulsation

ZHAO Bo1,CHEN Chang-sheng2,FU Dong-liang2,WANG Qiang2
(1.Naval Deputy Office at 704 Institute,Shanghai 200031,China; 2.704 Research Institute of CSIC,Shanghai 200031,China)

Abastract:The pressure pulsation of unsteady fluid flow in pumps can induce structural vibration.So,its calculation method is worth studying.In this paper,the structural vibration response induced by fluid pressure pulsation in an axial flow pump was simulated through the finite element analysis software,and the calculation data was processed and compared with the test results.The accuracy and feasibility of the method was analyzed.The results show that the calculation method can be used for forecasting blade-pass frequency vibration,and the ability of this method for high-order harmonic-frequency recognition can be improved by increasing the number of sampling points.

vibration and wave;axial flow pumps;pressure pulsation;structural vibration;transient analysis

O422.6

A

10.3969/j.issn.1006-1335.2015.02.007

1006-1355(2015)02-0028-04+40

2014－06－04

赵博（1977－），男，吉林长春人，工程硕士，主要从事舰船机电研究及产品质量控制。E-mail:jzzx704@163.com