一种基于改进的遗传算法的癌症特征基因选择方法

范方云， 孙 俊， 王梦梅

(江南大学物联网工程学院，江苏无锡214122)

随着基因表达谱技术的推广，利用DNA芯片可以在一次实验中同时获得成千上万个基因的表达水平［1］。依据基因表达谱建立分类模型，实现对癌症类型的识别与判断，对癌症的诊断与治疗具有重要意义［2-3］。然而，基因表达谱数据维度高，样本量很少，且分布不均匀，只有少量的基因真正具有分类信息。在进行癌症分类时，大量冗余特征会严重影响分类效果，而且增加了计算时的复杂度。所以，如何选择出对分类具有积极作用的基因是建立有效分类模型的关键所在。国内外学者在这方面已经进行了大量研究［4-6］。张靖等［7］利用信噪比指标过滤无关基因，采用迭代Lasso方法进行冗余基因的剔除，结合SVM分类器在数据Leukemia，Prostate，Colon 上分别获得了 98．61%，96．08%，90．32% 的分类正确率;张焕萍等［8］提出了离散粒子群和支持向量机封装模式的BPSO-SVM特征基因选择方法，在数据集Colon上用34个特征基因子集获得了89．67% 的平均正确率。目前，多种特征选择方法的使用已经取得了较好的分类效果，但存在的问题依然很明显，即如何在提高分类正确率的同时降低基因子集的规模，换言之，如何用最少的基因得出最好的分类效果。

文中提出了基于改进的遗传算法的癌症特征基因选择方法。通过改进遗传算法的交叉和变异操作，使得遗传算法在搜索分类基因时具有更强的全局搜索能力，并且避免了局部收敛。同时根据基因子集的特点，增加了最优个体变异策略，提高算法找到最优解的可能性。此外，将分类正确率和基因个数同时考虑，进行多目标优化，使用SVM分类器进行留一法交叉验证。同时，实验使用基本遗传算法进行特征选择，将两种遗传算法的表现进行比较。结果表明，改进的遗传算法相比于基本的遗传算法明显具有更优的分类正确率和更小的基因子集。

1 遗传算法的基本原理

遗传算法(Genetic Algorithm，GA)是一个经典的随机搜索与优化算法，是建立在Darwin的进化论和Mendel的遗传学说基础上的。1975年，密执安大学的教授Holland与其学生创建了该算法［9］。从此，对遗传算法的研究引起了国内外诸多学者的关注。

与传统的搜索算法不同，遗传算法是从一组随机产生的初始解开始搜索过程的。这组初始解被称为群体，初始解的个数就是群体的大小。群体中的每个个体都是目标问题的一个解，称为染色体。这些染色体在后续过程中不断进化迭代，这个过程称为遗传。遗传算法的进化过程主要是通过3种操作实现，分别为选择、交叉、变异。选择、交叉或者变异运算产生的下一代染色体，称为后代。染色体的好坏用适应值进行衡量。每个染色体都可以计算适应值，计算适应值的函数称为适应值函数。根据适应值的大小从上一代中选择个体，再通过交叉和变异，得到后代;再继续进化，经过若干代之后，算法收敛于最好的染色体。

利用遗传算法解决某个实际问题通常从初始化一个种群开始。所以解决某个实际问题，首先就是根据这个实际问题进行个体编码，然后生成初始种群，再对染色体进行选择、交叉以及变异操作。

2 遗传算法的改进

为了增加遗传算法的全局搜索能力和局部搜索能力，文中提出了3种改进策略:均匀交叉策略、变异概率的非线性递增策略和最优个体变异策略。均匀交叉策略是指两个配对个体的每一位都以相同的概率进行交换，从而形成两个新的个体;变异概率的非线性递增策略是变异概率随着种群进化代数的增加而非线性的增加;最优个体变异策略是对每次迭代的最优个体进行变异，增加算法找到全局最优解的可能。实验结果表明，3种改进策略的提出有效地提高了基本遗传算法在选择特征基因的能力。

2．1 均匀交叉策略

在改进的遗传算法中，使用均匀交叉，而不是传统的单点交叉。均匀交叉是指两个配对个体的每一位都以相同的概率进行交换，从而形成两个新的个体。具体的操作如下:首先随机生成一个与个体长度相等的二进制串，称为掩码。掩码的第i位与个体的第i位相对应。对于个体A和B，当掩码的第i位为1时，不交换A和B的第i位。当掩码的第i位为0时，交换A和B的第i位。具体如图1所示。

图1 个体A和个体B进行均匀交叉产生个体X和YFig．1 Individual A and individual B produce individual X and Y by uniform crossover

2．2 变异概率的非线性递增策略

变异概率是遗传算法中一个重要的参数，它直接影响到搜索算法的收敛性和算法搜索的性能。变异概率大，会使得算法不断搜索新的空间，增加解的多样性。但是，较大的变异概率会影响算法的收敛性。因此，在解决实际问题中，取变异概率为一个较小的值，一般在0．001～0．05之间。

在改进的遗传算法中，提出了一种变异概率的非线性递增策略，即变异概率随着种群进化代数的增加而非线性增加。具体表示为

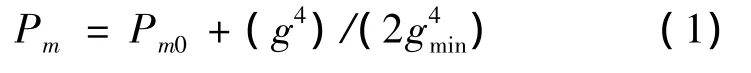
式中:g为当前进化代数;gmax为最大进化代数。

非线性递增变异概率曲线如图2所示。

图2 非线性递增变异概率曲线Fig．2 Probability curve of the nonlinearity increasing mutation

由图2可以看出，在种群进化初期，变异概率较小，为0．05，加速算法向最优解靠拢;随着进化代数的增大，变异概率逐渐增大。改进后，算法易搜索到新解，有利于算法摆脱局部最优，在一定程度上抑制了早熟收敛。

2．3 最优个体变异策略

最优个体是指对环境适应能力最强，能够得到最好适应值的个体。最优个体就是搜索空间中的最好位置。在本课题中，癌症特征基因提取的目标是选择出一个最优特征基因子集，这个特征基因子集具有最强的分类信息，即用该特征基因子集进行癌症数据集的分类能得到最好的分类效果。与其他寻优问题不同的是，最优特征基因子集与次优特征基因子集之间往往具有很大的重叠，在整个搜索空间中的位置是十分接近的，两者之间可能有少数几个基因存在差别。因此，充分利用每次迭代后得到的最优个体，在最优个体上进行随机位置变异，能够增大寻找到全局最优个体的可能性。做法是，随机选择每次迭代后的最优个体中的某些位置进行变异，如果变异后的新个体确实具有更好的适应值，则代替原最优个体。否则，不做改变。具体操作如下:

1)获取本次迭代的最优个体gbest;

2)随机选择gbest的1个或者2个位置进行变异，得到newgbest;

3)如果 newgbest的适应值大于 gbest，则用newgbest替换gbest，否则不做任何操作。

3 实验设计

为了证明改进后的遗传算法具有更好的性能，实验中同时使用基本遗传算法进行特征基因的选择。因为两个算法在同样的软硬件环境中进行，而且使用相同的参数、数据集、预处理和适应值函数，所以结果具有可比性。鉴于随机算法的随机特点，实验对两种算法用每一个癌症数据集进行25次独立实验，以便比较算法的性能。

3．1 参数设置

改进的GA和基本的GA中使用的参数见表1。这些参数都是经过多次测试，能够保证得到较好的分类结果。

表1 算法参数Tab．1 Parameters of the algorithm

3．2 实验数据集

大量公开的癌症基因表达研究实验已经提供了许多DNA微阵列数据集。文中使用了其中5个癌症基因表达谱数据集，分别为白血病数据集(Leukemia)，前列腺癌数据集(Prostate)，结肠癌数据集(Colon)，肺癌数据集(Lung)和淋巴癌数据集(Lymphoma)。所有这5个数据集都可以从如下网址获得:http://linus．nci．nih．gov/ ～ brb/DataArchive_New．html。表2给出了这5个数据集的详细信息。其中，类别1和类别2中括号中的数字是该类样本的个数。

表2 实验数据集描述Tab．2 Description for the experimental datasets

3．3 预处理

由于原始的癌症数据集中有几千甚至几万个基因，这些基因中含有大量的冗余基因，这些冗余基因将严重影响特征选择的效果，所以在选择特征基因之前，先对数据集进行初步筛选。首先对数据进行标准化处理，消除量纲对分类的影响。采用T检验进行初步筛选。根据T检验的P值对基因进行排序，选择P值最小的100个基因作为遗传算法的全局搜索空间。至此，已经去除了数据集中大量的冗余基因。

3．4 适应值函数

在遗传算法中，适应值用于评价个体的优劣，利用适应值函数计算个体的适应值。在本方法中，粒子Xi是一个表示基因子集的二进制串，SVM分类器使用每个粒子表示的基因子集进行留一交叉验证(Leave-one-out Cross Validation，LOOCV)。文中设适应值函数为

其中，accuracy为LOOCV正确率;feature_number为基因子集中基因的个数;α和β为权重参数，本方法中分别将 α 设为0．6，β 设为0．4。因为，相比于基因子集的规模，数据集的分类正确率是该实验研究更加关注的内容，所以设置α值为0．6大于β值0．4，这样可以更好地控制数据集分类正确率在评价基因子集中的主要地位。因为适应值越大，基因子集越优，所以该适应值函数利于最大化分类正确率和最小化特征基因的规模。

3．5 改进的遗传算法选择基因

T检验进行初步筛选之后，已经排除了原始数据中大部分无关基因。下面利用改进的遗传算法对数据集进行进一步的筛选，选择出真正具有分类信息的基因。

利用改进后的遗传算法作为特征选择的全局搜索引擎，SVM作为特征基因子集的评价分类器。设种群中的个体数为20，使用改进的遗传算法对种群进行选择交叉变异操作，设置最多进化代数为100。当满足结束条件时，结束迭代。在本算法中设置结束条件为:①LOOCV分类正确率≥99．99% 且选择的基因个数≤10时;②达到最多进化代数。满足两个条件中的任何一个，即可结束迭代过程。迭代结束后，输出最终选择的基因，至此一次实验结束。因为遗传算法的随机性，为了得到更加可靠的结果，对每一个数据集进行25次独立实验。算法流程如图3所示。

图3 算法流程Fig．3 Flowchart of the algorithm

4 结果分析

4．1 LOOCV正确率分析

表3给出了改进的GA+SVM与基本GA+SVM对癌症数据分类正确率的比较。其中最优为25次独立实验中的最优LOOCV正确率，平均为25次独立实验LOOCV正确率的平均值。

表3 改进的GA+SVM与基本的GA+SVM对癌症数据LOOCV正确率比较Tab．3 Comparison of LOOCV accuracy for each dataset between the improved GA+SVM and the basic GA+SVM 单位:%

由表3中可以看出，改进的GA+SVM在所有的5个数据集上都比基本的GA+SVM得到了更好的结果。

图4给出了最终选择出的基因子集中基因的个数。其中选择基因个数为相应癌症数据集25次独立实验所得到基因子集的平均个数。

图4 改进的GA+SVM与基本的GA+SVM对癌症数据选择基因个数比较Fig．4 Number of the selected genes for each dataset between the improved GA+SVM and the basic GA+SVM

由图4中可以看出，改进后的GA+SVM在5个数据集上都比基本的GA+SVM得到了更小的基因子集规模。

4．2 鲁棒性分析

除了算法的性能，算法在独立执行多次产生相同或相近结果的能力即鲁棒性也是衡量算法的一个重要指标。包括实验所研究的遗传算法在内的元启发式方法更是如此。表4给出了改进的GA+SVM与基本的GA+SVM鲁棒性的比较。其中，标准差是25次独立实验的LOOCV正确率的标准差。

表4 改进的GA+SVM与基本的GA+SVM鲁棒性比较Tab．4 Robustness between the improved GA+SVMand the basic GA+SVM

由表4可以看出，在数据集Leukemia，Colon中，改进的GA+SVM算法鲁棒性明显比基本GA+SVM好;两个算法在Lung数据集上都得到了25次100%的正确率;对于Prostate和Lymphoma数据集，虽然改进的GA+SVM得到的标准差比基本GA+SVM更大，但是前者找到了更好的基因子集，由此得到了更好的平均正确率。

4．3 生物意义分析

将所有基因子集中的基因进行统计，列出每个数据集出现频率最高的5个基因和相应的基因描述。表5给出了Colon和Lung数据集的基因子集中出现频率最高的5个基因及其基因描述。

表5 Colon和Lung数据集的基因子集中出现频率最高的5个基因Tab．5 Top 5 genes with the highest selection frequency of the Colon and the Lung

图5和图6给出了表5中的10个基因的基因表达在热点图中的表现。由图5和图6可以明显看出，对于Colon和Lung数据集，5个基因在两个类别间有明显的表达差异，即用改进的遗传算法选择出的这5个基因具有明显的分类信息。

5 结语

对基本遗传算法的交叉和变异操作进行改进，将改进后的遗传算法和基本遗传算法用于对5个癌症数据集进行基因选择和分类。对比两种算法，实验结果充分证明了改进后的遗传算法在搜索性能、鲁棒性上都有明显的优势，且选择出的基因的确具有明显的分类信息。

图5 Colon数据集选出的基因的热点图Fig．5 Heat map of the genes selected from the Colon dataset

图6 Lung数据集选出的基因的热点图Fig．6 Heat map of the genes selected from the Lung dataset

［1］Lander E S．Array of hope［J］．Nature Genetics，1999，21:3-4．

［2］Ramaswamy S，Golub T R．DNA microarrays in clinical oncology［J］．Journal of Clinical Oncology，2002，20(7):1932-1941．

［3］DeRisi J，Penland L，Brown P O，et al．Use of a cDNA microarray to analyse gene expression patterns in human cancer［J］．Nature Genetics，1996，14(4):457-460．

［4］刘金勇，郑恩辉，陆慧娟．基于聚类和微粒群优化的基因选择方法［J］．数据采集与处理，2014，29(1):83-89．LIU Jinyong，ZHENG Enhui，LU Huijuan．Gene selection based on clustering method and particle swarm optimization［J］．Journal of Data Acquisition and Processing，2014，29(1):83-89．(in Chinese)

［5］于彬，张岩．基于 GA-SVM方法的结肠癌基因表达谱数据分析［J］．青岛科技大学学报:自然科学版，2013，33(6):587-592．YU Bin，ZHANG Yan．Analysis of colon cancer gene expression profiles based on GA-SVM method［J］．Journal of Qingdao University of Science and Technology:Natural Science Edition，2013，33(6):587-592．(in Chinese)

［6］徐久成，徐天贺，孙林，等．基于邻域粗糙集和粒子群优化的肿瘤分类特征基因选取［J］．小型微型计算机系统，2014(11):31．XU Jiucheng，XU Tianhe，SUN Lin，et al．Feature selection for cancer classification based on neighborhood rough set and particle swarm optimization［J］．Mini-Micro Sysitms，2014(11):31．(in Chinese)

［7］张靖，胡学钢，李培培，等．基于迭代 Lasso的肿瘤分类信息基因选择方法研究［J］．模式识别与人工智能，2014，27(1):49-59．ZHANG Jing，HU Xuegang，LI Peipei，et al．Informative gene selection for tumor classification based on iterative lasso［J］．Pattern Recognition and Artificial Intelligence，2014，27(1):49-59．(in Chinese)

［8］张焕萍，宋晓峰，王惠南．基于离散粒子群和支持向量机的特征基因选择算法［J］．计算机与应用化学，2007，24(9):1159-1162．ZHANG Huanping，SONG Xiaofeng，WANG Huinan．Feature gene selection based on binary particle swarm optimization and support vector machine［J］．Computers and Applied Chemistry，2007，24(9):1159-1162．(in Chinese)

［9］Holland J H．Adaptation in Natural and Artificial Systems:An Introductory Analysis with Applications to Biology［M］．Ann Arbor:University Michigan Press，1975．