边界控制系统的干扰解耦

李 凯， 栾小丽， 刘 飞

(江南大学自动化研究所，江苏无锡214000)

实际工业过程中，存在很多控制作用加在控制对象边界上的无穷维系统。如热传导过程和橡胶工业中轮胎硫化的过程，热量是从边界传递到内部的。1968 年，Fattorini［1］首次提出边界控制系统概念，此后，边界控制系统被人们广泛关注。Glowlnski R［2］讨论了波方程和热方程在边界控制下的能控性问题，给出边界控制下系统精确能控和近似可控问题的解;Doubova A等［3］针对边界控制下非线性热方程能控性问题，给出了系统能控的充分条件。进而，Seidman T I［4］针对椭圆型方程边界反馈条件下系统可镇定问题进行了研究，给出解指数趋于零的代数条件。最近，Mohamed B G［5］研究无穷阶时滞双曲线型系统的边界控制问题，给出系统的最优控制的充要条件;Deutscher J［6］给出了线性边界控制系统的有限维对偶状态反馈律。

已有的边界控制系统研究成果，从线性到非线性，从系统分析到控制器设计，主要集中在能控性、最优控制、反馈镇定等方面，均未考虑边界控制系统的干扰解耦问题。然而，干扰解耦在控制系统分析与设计中占有很重要的位置。文献［7-10］给出了解决一般线性和非线性系统的干扰解耦问题的方法。

文献［11-13］针对无穷维系统进行干扰解耦问题的研究。目前，对于边界控制系统控制问题，通常将偏微分方程改成状态方程。但是，得到的状态方程中控制算子是无界的［14］。然而，在干扰解耦问题研究中，无界控制算子会导致输出算子的最大子空间不存在［15］，难以给出系统可干扰解耦的充分条件;此外，在无穷维系统中计算子空间需要严格的假设条件，且相对于在有限维系统中计算子空间，计算过程复杂繁琐［10，15-17］。

针对上述问题，文中基于有界控制算子转换技术［18］和希尔伯特空间射影法，对边界控制系统进行干扰解耦研究。先利用有界控制算子转换技术将边界控制系统转换成等价有界系统，再应用希尔伯特空间射影法对等价有界系统进行处理，将边界控制系统的干扰解耦转化为有限维等价有界系统的干扰解耦问题。基于几何子空间理论［19］，推导出有限维等价有界系统可干扰解耦的充分条件。进一步证明，若有限维等价有界系统可干扰解耦，则边界控制系统也可干扰解耦。

1 有界算子转换

文中使用的符号说明如下:

D(A)为算子A的定义域;L(X，Y)为从线性空间X到线性空间Y的线性有界算子空间;⊕为直和;T:X→Y为线性映射;‖‖表示范数;Im E为算子E的象空间;Ker D为算子 D零空间;〈·，·〉为内积。

考虑如下边界控制系统［1］

其中，a在Hilbert空间X中是线性闭算子;τ为一个线性边界算子，τ:X→Y1，其定义域D(a)⊆D(τ)，y∈Y，u∈U，x0∈X，q∈Q，a:X→X，E∈L(Q，X)，G∈L(U，Y1)，D:X→Y;X，Y，Y1，Q为可分实Hilbert空间，U∈Rm。

进一步地，定义算子A为空间X中强连续C0半群无穷小生成元，A的定义域为

且在定义域D(A)中，满足Ax=ax。

注1 a为偏微分算子，τ为微分算子。在D(a)范数下，τ/D(a)是连续的。

边界控制系统的干扰解耦问题就是当q为干扰输入时，设计一个反馈控制律u，使得输出y与干扰q无关。

为对边界控制系统的干扰解耦问题进行分析，首先，对系统式(1)进行有界算子转换，进行如下假设:

1)存在有界算子B，B∈L(U，X)，u∈U，满足Bu∈D(a)和

2)N=aB，N ∈ L(U，X)，N 是有界的。

令x=v+Bux(0)=v(0)+Bu(0)，综合上述假设条件以及式(1)，可得方程

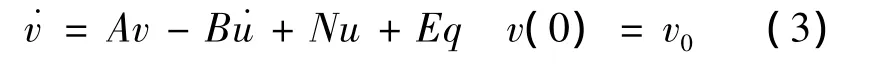
对式(1)和式(3)进行增广变换，得到边界控制系统在状态空间˜X=X⊕Rm下的有界拓展形式

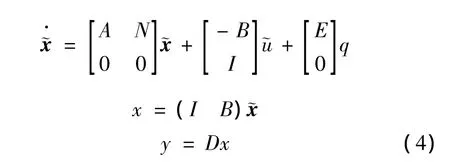
其中

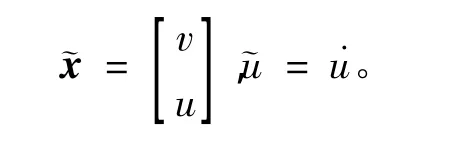
对式(4)进一步处理，可得

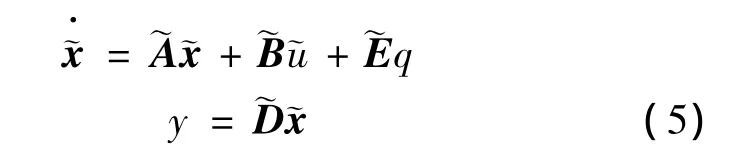
其中

注2 对于边界控制系统控制问题，由于控制算子是无界的。如果将其改写成状态方程系统，进行处理时，过程比较复杂，且难以被应用。文中采用有界控制算子转换技术，通过寻找有界算子对式(1)进行增广处理，得到一个有界拓展系统。综合比较式(1)和式(5)的输出，式(1)中输出y=Dx，式(5)中输出y=D(IB)x。可以明显得到，若式(5)中系统输出y=D(IB)x与干扰q无关，则式(1)中输出y=Dx也与干扰q无关，从而说明了将式(1)的干扰解耦问题转换为式(5)的干扰解耦问题的有效性。

2 干扰解耦分析

以有限近似方法为主要技术手段，进一步对式(5)进行射影处理，得到一个有限维等价有界系统，并推导出有限维等价有界系统可干扰解耦的充分条件;同时给出证明，当有限维等价有界系统可干扰解耦，原边界控制系统也可干扰解耦。

针对式(5)，采用希尔伯特空间射影法进行近似处理。

注3 利用希尔伯特射影法对等价有界系统进行近似处理，对有限维等价系统的干扰解耦问题进行研究。定理1给出了有限维近似系统可干扰解耦的充分条件;给出定理2，结合两个假设条件证明了有限维系统系可干扰解耦，等价有界系统也可干扰解耦，说明了希尔伯特空间射影法的有效性;给出定理3，证明了等价有界系统可干扰解耦，边界控制系统也可干扰解耦，说明了有界算子转换技术在文中的有效性。

3 实例

通过这个实例，给出其可干扰解耦的充分条件，验证了文中方法是有效的。

4 结语

文中讨论了边界控制系统下的干扰解耦问题，给出了边界控制系统可干扰解耦的充分条件。使用有限维近似方法，转换到在有限维系统中计算几何子空间，避免了在无穷维系统中计算几何子空间不存在或者计算过程很复杂等问题。有界控制算子转换技术，是对边界控制系统处理的一种特殊方法。如何得到边界控制系统在含有无界控制算子的标准状态方程下干扰解耦的解，还需要进一步研究。

［1］Fattorini H O．Boundary control systems［J］．SIAM Journal on Control and Optimization，1968，6(3):349-385．

［2］Glowlnski R．Boundary controllability problems for the waveand heat equation［J］．Lecture Notes in Control and Information Sciences，1992，178:221-237．

［3］Doubova A，Fernández-Cara E，González-Burgos M．On the controllability of the heat equation with nonlinear boundary fourier conditions［J］．Journal of Differential Equations，2004，196(2):385-417．

［4］Seidman T I．Boundary feedback stabilization of a parabolic equation［J］．Analysis and Optimization of Systems，1984，62:385-392．

［5］Mohamed B G．Boundary control problem of infinite order distributed hyperbolic systems involving time lags［J］．Intelligent Control and Automation，2012，3(3):211-221．

［6］Deutscher J．Finite dimensional dual state feedback control of linear boundary control systems［J］．International Journal of Control，2013，86(1):41-53．

［7］CHEN B M．Solvability conditions for the disturbance decoupling problems with static measurement feedback［J］．International Journal of Control，1997，68(1):51-60．

［8］王晓华，刘晓平．非线性广义时变系统的干扰解耦［J］．自动化学报，2000，26(6):798-802．WANG Xiaohua，LIU Xiaoping．Disturbance decoupling of nonlinear generalized time-varying systems［J］．Acta Automatica Sinica，2000，26(6):798-802．(in Chinese)

［9］ZOU Runmin，Malabre M．Almost disturbance decoupling and pole placement［J］．Automatica，2009，26(11):2685-2691．

［10］ZOU Runmin，Malabre M．Solution of the almost disturbance decoupling problem by state feedback［C］//Proceedings of the 31stChinese Control Conference．Hefei:IEEE，2012:273-278．

［11］Curtain R F．Decoupling in infinite dimensional［J］．System and Control Letters，1985，5(4):249-254．

［12］Curtain R F．Disturbance decoupling by measurement feedback with stability for infinite dimensional systems［J］．International Journal of Control，1986，43(6):1723-1743．

［13］ZHOU Xiuxiang．Approximations of infinite dimensional disturbance decoupling and almost disturbance decoupling problems［J］．Mathematical Control and Related Fields，2014，4(3):381-399．

［14］Emirsjlow Z，Townley S．From PDEs with boundary control to the abstract state equation with an unbounded input operator:a tutorial［J］．European Journal of Control，2000，6(1):27-49．

［15］Zwart H J．Geometric Theory for Infinite Dimensional Systems．Lecture Notes in Control and Information Sciences［M］．Berlin:Springer-Verlag，1989．

［16］Curtain R F．Invariance concept in infinite dimensions［J］．SIAM Journal on Control and Optimization，1986，24(5):1009-1030．

［17］Zwart H J．Equivalence between open-loop and closed-loop invariance for infinite dimensional systems:a frequency domain approach［J］．SIAM Journal on Control and Optimization，1988，26(5):1175-1199．

［18］Curtain R F．On semigroup formulations of unbounded observations and control action for distributed systems［J］．Mathematical Theory of Networks and Systems，1984，58:183-193．

［19］Wonham W M．Linear Multivariable Control:A Geometric Approach［M］．New York:Springer-Verlag，1979．