基于随机漂移粒子群优化算法的三维脑部磁共振图像分割

施佳佳， 孙 俊， 范方云， 王梦梅

(江南大学物联网工程学院，江苏无锡214122)

医学图像分割对临床辅助诊断、量化分析、精准放射治疗等具有重要的辅助意义。许多神经系统的疾病在临床研究上都伴随着脑部组织细微的异常变化。核磁共振成像(MRI)的分割目的在于把脑部图像分割成不同的组织，即分别为白质(WM)、灰质(GM)、脑脊液(CSF)3 类［1］。目前 MRI组织的分割已经成为大量医学研究算法的热点。其中，以定量描述局部依赖关系的马尔科夫随机场(Markov Random Field，MRF)模型，在表达灰度数据空间分布特征方面显现出良好的特性。由于MRF模型具有参数少、抗噪性良好等优点，它在计算机视觉中已经得到广泛应用［2］。在图像分割中，MRF可以视为一个寻找能量最优化的标记问题。由于MRF本身是一个先验模型，因此常采用最大后验概率(Maximum A Posterior，MAP)进行估计。在利用MRF-MAP框架分割图像时，整个标记问题最终转化为目标函数的极值优化问题。因此，目标函数的优化算法一直是医学图像分割中研究热点。

文中采用一种最新的随机漂移粒子群(Random Drift Particle Swarm Optimization，RDPSO)算法计算MRF模型中目标函数。在多维解空间中，RDPSO算法通过研究粒子在自由电场中的行为实现信息共享，从而取得更快的搜索速度，是一种全局性的优化算法［3］。RDPSO算法相对于标准粒子群算法(Particle Swarm Optimization，PSO)，具有收敛性强、全局搜索能力突出等特点。实验数据证明文中的算法能够取得更好的分割效果。

1 MRI分割中的MRF模型

1．1 MRF 模型

假设MRI图像定义在S={1，2，…，N}有限点阵上，X和Y表示两个随机场，它们的状态空间分别是L和D，其中

则对于∀i∈S满足Xi∈L，Yi∈D。令x表示X的一组配置，X是所有可能配置的集合，即

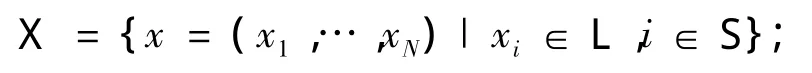
同样，令y为Y的一组配置，Y为所有可能配置的集合，

X表示图像类别标记，Y表示图像灰度。MRF中，S中的位置通过邻域系统相互关联，邻域系统定义为N={Ni，i∈ S}，这里 Ni为位置 i的邻域集，i∉ Ni。如果满足

则随机场X是S上关于邻域系统N的一个马尔可夫随机场(MRF)。

结合贝叶斯规则，采用最大后验概率估计(MAP)，可以将图像分割问题转化为求解图像的最大后验概率估计问题。因此，x可以通过最小化全局能量函数U(x)得到:

假设Y是通过加上一个独立的高斯噪声分布获得［4］，从而可以得到整个能量函数:

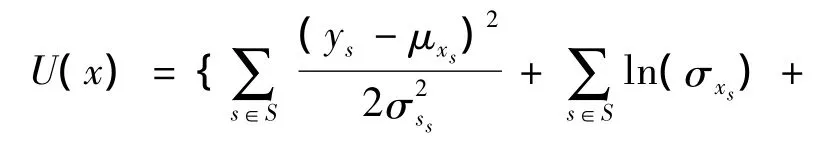
其中，μxs为类xs的平均值;σxs为类xs的方差;Vc(x)为定义在集簇c上的势能函数。因此，对MRF的研究主要集中在能量函数的计算和优化［5］。

1．2 势能函数

对应不同的邻域系统产生不同的MRF能量(见图1)。

图1 邻域系统Fig．1 Neighborhood system

V(x)由一组体现空间依赖关系的表达式定义。文中采用三维马尔科夫模型(3D MRF)的一阶邻域定义势函数V(x)，定义具体如下［6］:

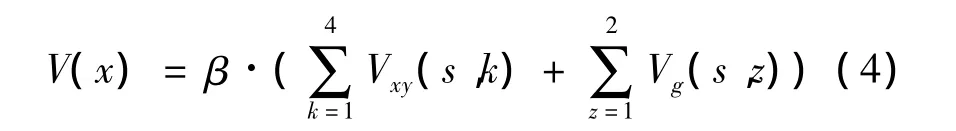
其中:s，k，z∈S;β为MRF的惩罚因子，一般取值为1/2;Vxy为二维平面内两个相邻点势能;Vg为上下两点势能。由于二维平面的势能相对上下势能较强，因此设置两个不同势能值

2 随机漂移粒子群算法

粒子群优化算法(PSO)是一种进化计算(evolutionary computation)算法［7］，源于科学家对鸟群捕食的行为研究，具有典型的生物群体智能特点［8］。系统初始化为一组随机粒子，通过计算函数适应值(fitness value)迭代搜寻最优值。每次迭代通过跟踪两个极值以更新自己。一个极值是粒子本身搜寻到的最优解，称为个体最优值;另一个是整个群体当前搜寻到的最优解，称为群体最优解。在PSO中，粒子群的规模为M，每个粒子i(i≤i≤M)代表D维空间中给定问题的一个可能的解，则每个粒子的位置表示为

3 基于RDPSO算法的混合分割算法

3．1 适应度函数的设计

3．2 算法实现

文中算法框架主要是用RDPSO算法对MRF中的适应度函数进行优化，算法步骤如下:

1)随机初始化粒子群，每个粒子代表2K个参数，定义为

其中，L={lk;k=1，2，…，K}为每种脑部组织的类别;K为分类数，一般设为4，考虑到脑部组织主要包括灰质、白质、脑脊液和背景。

2)对于每个粒子，根据式(17)分别计算适应值，根据式(6)和式(7)记录pbest和gbest，根据式(8)，式(11)(13)和式(14)，产生新粒子的位置和速度。

3)记录全局最优解和粒子群的最优适应值。

4)返回2)直至迭代次数结束。

4 实验结果与分析

4．1 评价标准

Dice相似系数(Dice Similarity Coefficient，DSC)是用以评价算法分割结果的一个标准，主要用于计算两幅二进制图片之间空间的重叠程度，定义如下

其中，U为算法分割结果;V为实际分割图像(ground truth)。DSC值在0到1间，值越大，分割精度越高。

同时，文中还采用错分率(Miss Classification Rate，MCR)标准评价分割算法的性能，定义如下:

其中，Smiss为分类错误的像素个数;Stotal为所有的像素。MCR值越小，分割结果越精确［10］。本算法分别与SA-MRF，PSO-MRF进行实验比较，以证明其优越性。

4．2 模拟脑部MR图像

模拟脑部 MR图像的数据集取自BrainWeb(http://brainweb．bic．mni．mcgill．ca/brainweb/)．Brainweb是一个公开的数据库，提供大量模拟的MR脑部图像。文中数据集由181×217×181个像素组成，层的厚度是1 mm，T1加权，实验数据选取了10个切片。图2给出了其中一个切片(Brainweb_70)的原图，ground truth和算法的分割结果。图3给出了10幅切片的DSC值。

图2 切片(Brainweb_70)的原图、标准分割图以及文中分割结果Fig．2 Brainweb_70＇s origin，ground truth and segmentation result

图3 DSC值对比Fig．3 DSC value comparison

由图3可以看出，文中算法的DSC值总体优于其他两种优化算法。图4给出了所有切片的平均错分率。由图4从中可以看出，文中提出的算法MCR值最小，能够取得更好的分割结果。

图4 错分率结果对比Fig．4 MCR result comparison

4．3 实际脑部MR图像

IBSR网站提供最新的临床脑部MR图像。文中下载的数据集中由256×256×56个像素组成，且已经被转化为TGA格式，便于采用Matlab进行处理。实验数据是对选取的10个切片进行分割，图5给出了IBSR中一个切片(raw_27)的分割结果。图6给出了每个切片的DSC值。由图6可以看出，文中算法整体优于其他两种优化算法。图7提供了所有切片平均的错分率。由于实验切片比较多，从图7可以看出平均错分率都比较低。其中文中算法的MCR值也是最小，远远优于其他两种算法，分割效果更加显著。

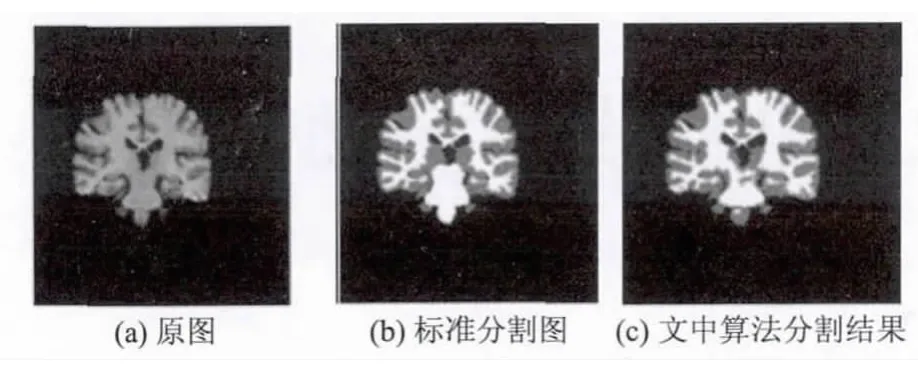
图5 切片(raw_27)的原图、标准分割图和文中算法分割结果Fig．5 Raw_27＇s origin，ground truth and segmentation result

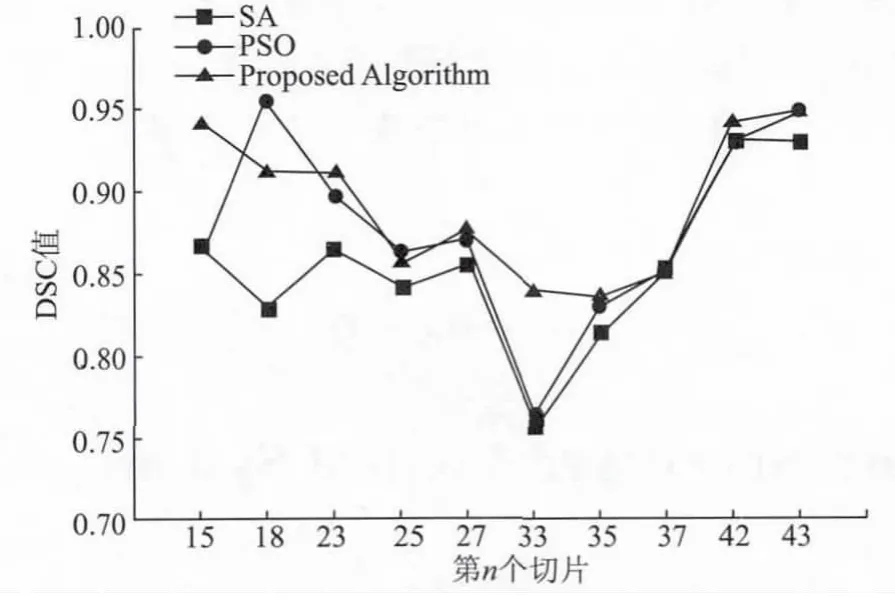
图6 DSC值对比Fig．6 DSC value comparison

图7 错分率结果对比Fig．7 MCR result comparison

5 结语

RDPSO作为一种全局随机优化算法，来源于对自由电子模型的研究，相对传统的全局优化算法(如SA和PSO)，在应用于MRF中解决脑部MR图像分类问题，拥有更快的收敛率和更好的分割效果。模拟和临床脑部MR数据的实验结果都证实了文中算法在分类模型中的优越性。

［1］Barker S，Rayner P J．Unsupervised image segmentation using Markov random field models［J］．Pattern Recognition，2000，33(4):587-602．

［2］宋艳涛，纪则轩，孙权森．基于图像片马尔科夫随机场的脑MR图像分割算法［J］．自动化学报，2014，40(8):1754-1763．SONG Yantao，JI Zexuan，SUN Quansen．Brain MR image segmentation algorithm based on markov random field with image patch［J］．Acta Automatica Sinica，2014，40(8):1754-1763．(in Chinese)

［3］SUN Jun，WU Xiaojun，Palade V，et al．Random drift particle swarm optimization［J］．ArXiv Preprint arXiv，2013，1306．2863．

［4］曹容菲，张美霞，王醒策，等．基于高斯-马尔科夫随机场模型的脑血管分割算法研究［J］．电子与信息学报，2014，36(9):2053-2060．CAO Rongfei，ZHANG Meixia，WANG Xingce，et al．A novel cerebrovascular segmentation algorithm based on gauss-markov random field model［J］．Journal of Electronics and Information Technology，2014，36(9):2053-2060．(in Chinese)

［5］靳华中，叶志伟，柯敏毅，等．结合MRF模型与粒子群优化算法的遥感影像纹理分割［J］．计算机应用，2010，30(9):2461-2463．JIN Huazhong，YE Zhiwe，KE Minyi，et al．Combination of MRF model and particle swarm optimization algorithm for texture segmentation of remote sensing images［J］．Journal of Computer Applications，2010，30(9):2461-2463．(in Chinese)

［6］Solomon J，Butman J A，Sood A．Segmentation of brain tumors in 4D MR images using the hidden Markov model［J］．Computer Methods and Programs in Biomedicine，2006，84(2):76-85．

［7］SHI Y，Eberhart R C．Empirical study of particle swarm optimization［C］//Proceedings of the 1999 Congress on Evolutionary Computation．Washington，DC:IEEE，1999．

［8］ZHAO B，GUO C X，BAI B R，et al．An improved particle swarm optimization algorithm for unit commitment［J］．International Journal of Electrical Power and Energy Systems，2006，28(7):482-490．

［9］SUN J，Palade V，CAI Y，et al．Biochemical systems identification by a random drift particle swarm optimization approach［J］．BMC Bioinformatics，2014，15(Suppl 6):S1．

［10］王文辉，冯前进，刘磊，等．基于类自适应高斯-马尔可夫随机场模型和EM算法的MR图像分割［J］．中国图象图形学报，2008，13(3):488-493．WANG Wenhui，FENG Qianjin，LIU Lei，et，al．Segmentation of brain images through class-adaptive gauss-markov random field model and the EM algorithm［J］．Journal of Image and Graphics，2008，13(3):488-493．(in Chinese)