单相逆变器小波占空比跟踪调制策略

宁 振， 吴 雷

(江南大学轻工过程先进控制教育部重点实验室，江苏无锡214122)

逆变(DC-AC)技术是电力电子技术的重要组成部分，广泛应用于并网发电、电机调速、感应加热等领域［1-3］。调制策略作为逆变器控制方法的核心部分，对逆变器工作性能有着重要影响。良好的调制策略对于提高直流母线电压利用率、降低开关损耗、减小谐波污染具有重要作用。目前常用的调制策略主要包括SPWM、SVPWM及其优化算法。

为了进一步提高逆变器工作效率，Saleh等提出新型调制技术WM［4-6］，降低了输出电压总谐波畸变率，但该调制策略采样组数设定受到限制，并且引入大量低次谐波。文献［7-8］引入系数改善采样信号时间间隔，降低了输出电压低次谐波含量，但电压调制比减小，输出电压总谐波畸变率明显增加。文献［9］采用新尺度设定方法，采样组数设定灵活，但采样尺度为非整数，运算复杂，数字化实现困难。

文中分析了WM逆变器电压输出占空比特性，拟开发一种占空比规则变化进而降低电压低次谐波的调制技术，同时期望该方法能够获得较低的总谐波畸变率。

1 WM设计原理

WM的主要思想是将逆变器调制等效为基于非均匀采样的小波变换:逆变器开关动作过程看作是对调制信号非均匀采样，再经小波变换重构调制信号的过程。

1．1 非均匀采样非二进小波重构

逆变器PWM驱动信号为变宽度脉冲序列，根据小波变换原理，对调制信号进行非均匀采样，因此采用非二进小波函数组。Haar小波函数尺度在时域中表现为方波形式

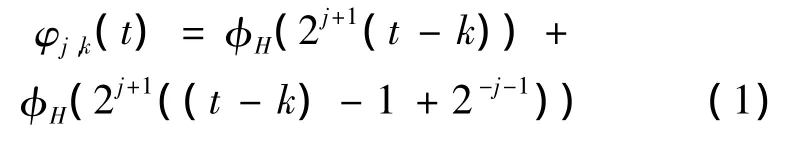
式(1)中，当 t∈［0，1)，ΦH(t)=1，其他情况ΦH(t)=0;j，k分别为尺度系数和平移系数。由Haar小波合成的对偶小波函数为

WM尺度j以1为步长随基波周期性变化，因此小波函数组为非二进的。不难证明，Haar小波尺度函数及其对偶小波函数随系数j，k伸缩平移，且满足对偶条件。根据离散小波理论，任意连续信号都能够用适当小波分解并由其对偶小波函数重建，可采用Haar小波函数对调制信号s(t)离散小波变换。

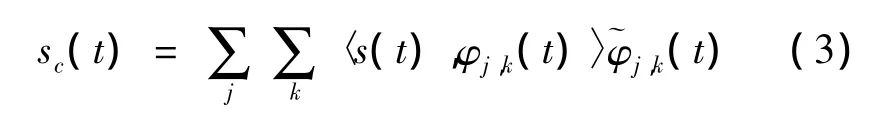
式(3)中内积为

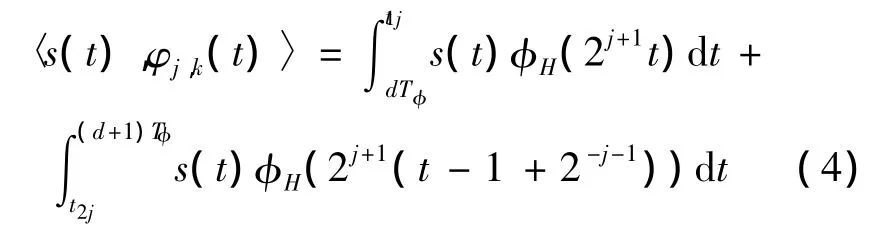
将调制周期T等分为D个采样组，T0=T/D，T0为采样周期，每个采样周期对应一个j，确定一个尺度函数。WM通过小波尺度函数对调制函数采样，再利用其对偶小波函数重建采样信号。每个T0尺度函数采样两次，确定一个对偶函数，该对偶函数就是一T0内的重构函数。利用Haar小波对调制信号的采样与重构如图1所示。

从图1看出，对偶小波重建信号表现为逆变器输出方波电压的性质，可作为WM逆变器的输出电压。T0固定时，对偶函数决定每个采样周期信号占空比，因此通过控制每个采样周期的对偶函数，即可实现WM逆变器输出电压占空比的控制。正弦信号具有1/4周期对称性，当调制信号为正弦信号时，控制(0，T/4］，(T/2，3T/4］占空比逐渐增大，(T/4，T/2］，(3T/4，T］占空比逐渐减小，实现一个调制周期内单相WM逆变器的控制。

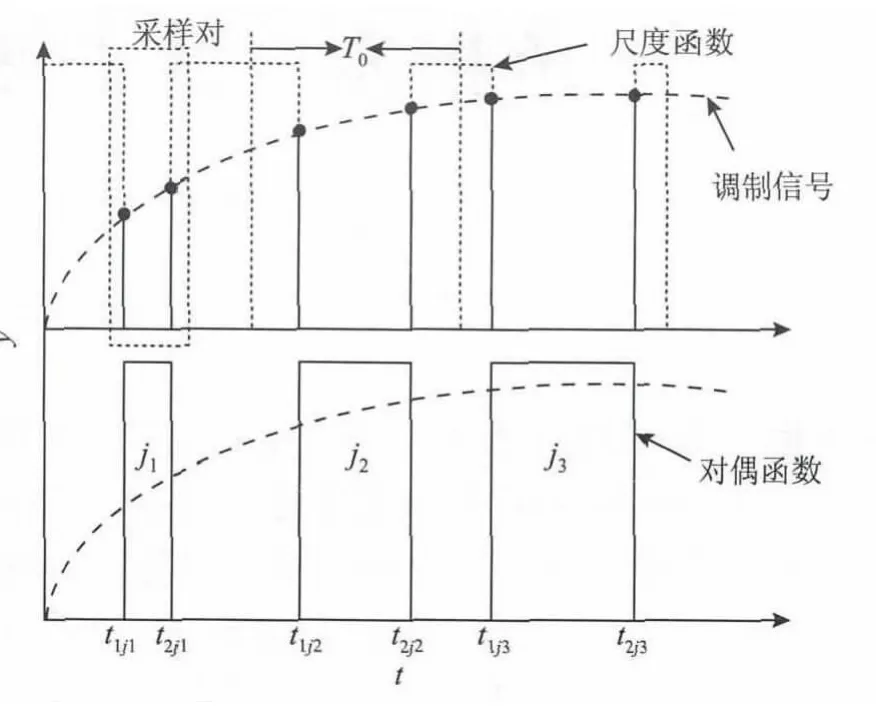
图1 Haar小波函数采样与重构Fig．1 Sampling and reconstruction

1．2 单相WM逆变器占空比跟踪的实现

每一采样周期WM逆变器输出电压上升沿跟下降沿时刻由Haar对偶小波函数决定。由式(2)可得

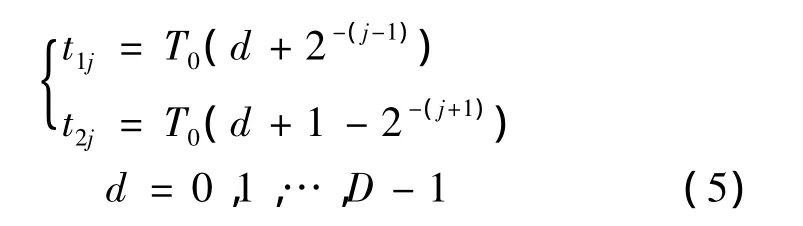
式(5)中，d为一调制信号周期内采样周期序列数。由式(5)可知，每个采样周期WM逆变器输出电压占空比为1－2－j。逆变器输出理想值等效为调制信号，根据PWM思想，占空比Q满足

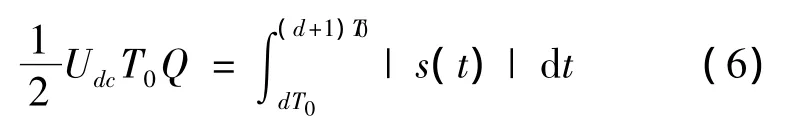
式(6)中，Udc为直流母线电压，s(t)为调制信号。采样周期T0为足够小时，整理式(6)得

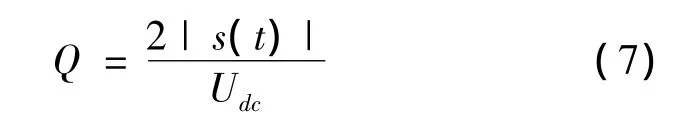
式(7)表明，理想情况下逆变器输出电压占空比变化规律与调制信号同步，特别地，当调制信号为正弦信号时，占空比按正弦规律变化。考虑到数字化实现方便，尺度j设定线性变化，将Haar对偶小波函数改造为

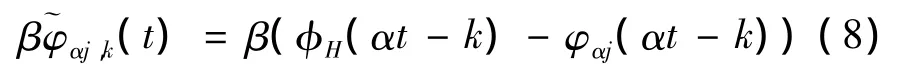
根据式(8)，前1/4正弦周期内，逆变器输出电压占空比满足

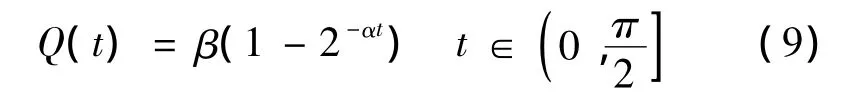
选取适当的参数，使Q最大程度逼近正弦信号。文中采用 y=sin(t)为参考信号，取 α=1．618 9，β =1．207 1，使两曲线所夹面积最小，认为Q较大程度逼近正弦参考信号。

为了进一步减小Q与参考信号的误差，引入误差函数Δ(t)=(Q－sin(t))/Q，分析表明，t较小时Δ(t)近似为二次多项式，当 α =1．618 9，β =1．207 1，Δ(t)≈0．282 7t2－ 0．666 2t+0．348 8，带入式(9)，可得

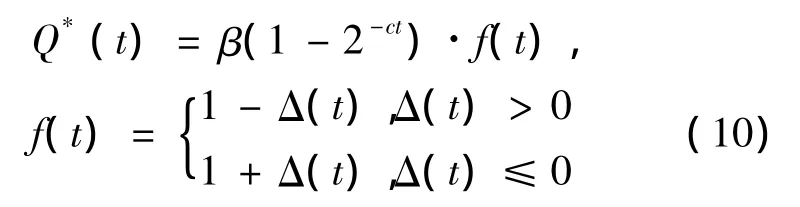
占空比函数Q，Q*如图2所示。

图2 占空比函数Fig．2 Function of duty ratio

如图2(a)所示，Q(t)与参考正弦函数有一定差距，但其占空比运算简便，易于实现;Q*(t)由于引入Δ，运算相对复杂，但与参考正弦函数几乎完全吻合。图2(b)中二次拟合函数在0附近虽然误差比较大，但此时占空比很小，造成的实际误差较小，因此可以根据式(9)，(10)对跟踪逆变器输出电压占空比。综合式(8)～(10)，式(9)确定的逆变器开关动作时刻为

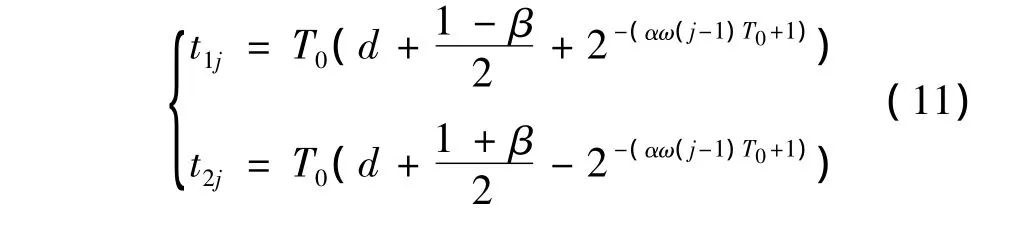
式(10)确定的逆变器开关动作时刻为

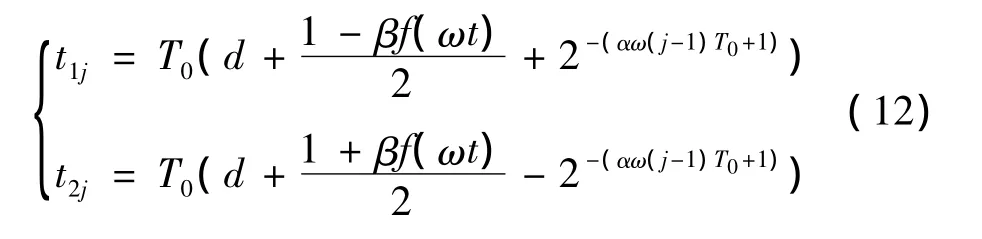
式(11)～(12)中，t1j，t2j分别为逆变器开关管导通关断时间，T0为一个采样周期，ω为调制信号角频率。单相全控型逆变器电路拓扑如图3所示。根据t1j，t2j控制V1～V4的导通关断，即可实现对逆变器输出电压占空比的跟踪控制。

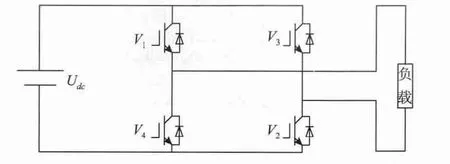
图3 逆变器拓扑Fig．3 Single-phase inverter

基于t1j，t2j设计WM单相逆变器调制算法流程如图4所示。图中s(t)为调制信号，s1～s4为逆变器开关管V1～V4驱动信号。每结束一个T0，更新j，d，生成新的Haar小波尺度函数和对偶函数，进行新一轮采样与重建。当一个 T结束，初始化 j，d，t，进入下一个调制周期。

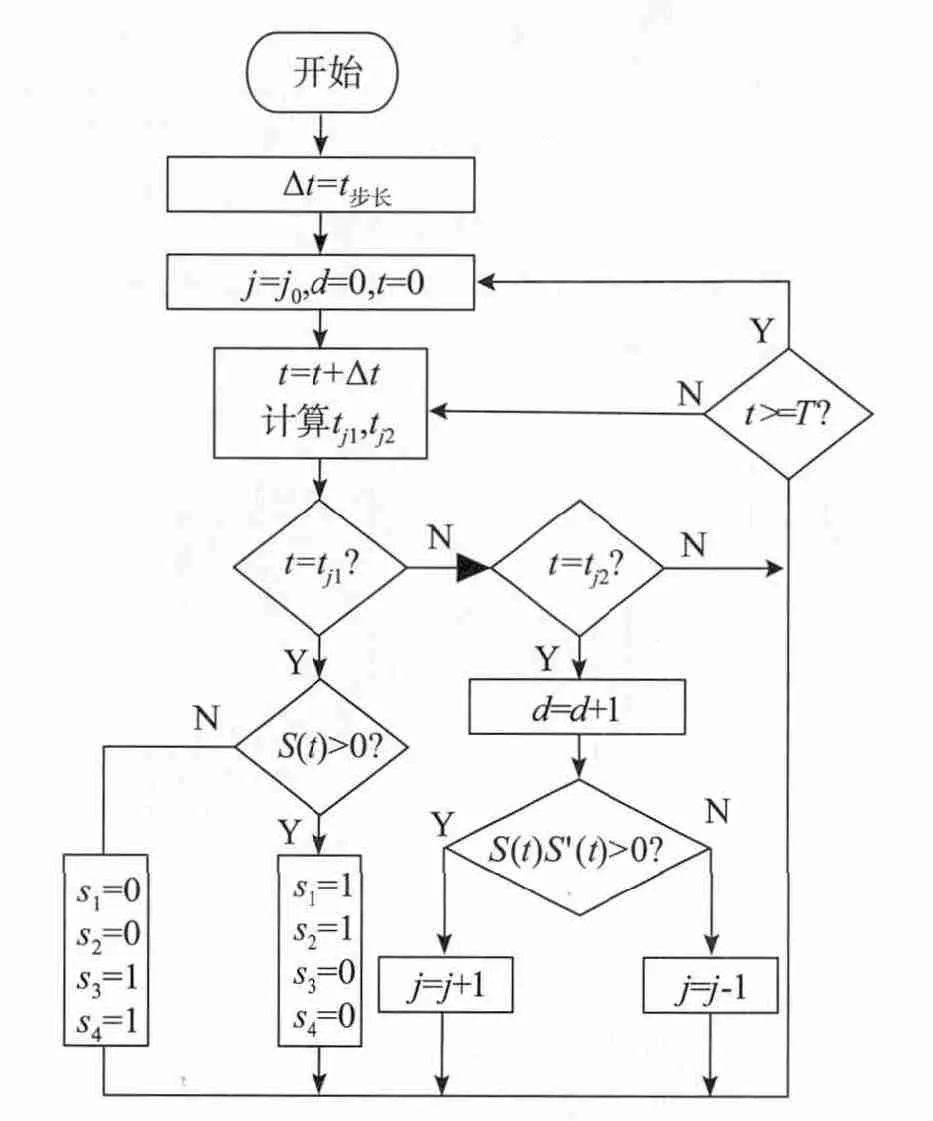
图4 WM算法流程Fig．4 Flowchart for the WM algorithm

2 仿真实验

研究采用Matlab搭建单相WM逆变器仿真模型，设定采样尺度值j随调制信号周期性变化:(0，T/4］、(T/2，3T/4］内 j从 1 增大到 J，J=(D+2)/4;(T/4，T/2］、(3T/4，T］内 j从J － 1 减小到1。采用傅里叶分析法对比不同的WM仿真结果，仿真和傅里叶分析结果如图5～7所示，图中h3，h5，h7分别为3，5，7次谐波畸变率。

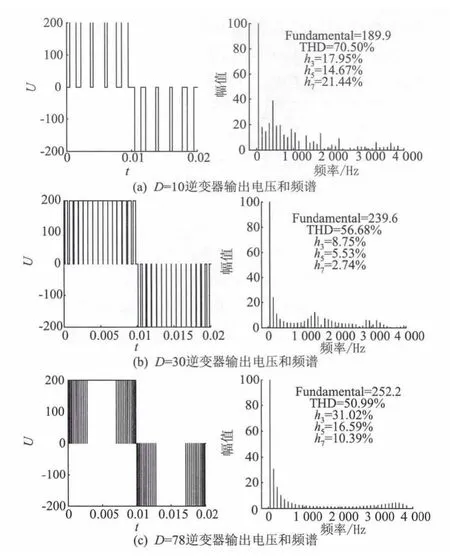
图5 传统WMFig．5 Traditional WM inverter output and frequency spectrum

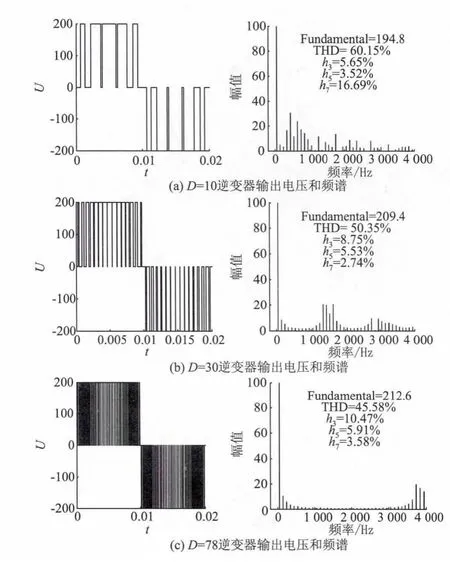
图6 按Q跟踪占空比的WMFig．6 Q tracking duty rotio of WM

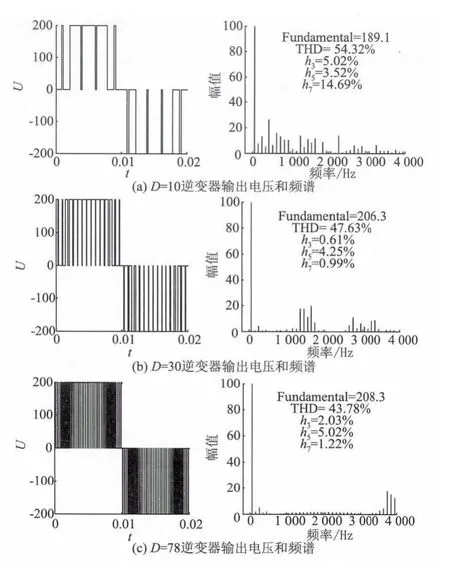
图7 按Q*跟踪占空比的WMFig．7 Q*tracking duty ratio of WM

对比图5～7可知，采用占空比跟踪技术的WM逆变器输出电压的低次谐波含量和谐波总畸变率明显降低，基波电压幅值略有下降但变化不大;按Q*跟踪占空比的WM逆变器输出电压频谱分布优于按Q跟踪的逆变器输出。图8为总谐波畸变率统计折线图。由图8可知，随着采样组数的增加，两种逆变器输出电压频谱差距逐渐减小。因此应根据WM的运算量与调制效果，选取适当的占空比跟踪方式。

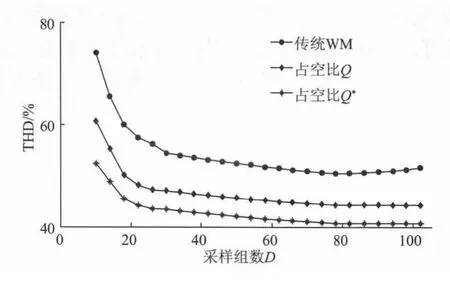
图8 总谐波畸变率折线Fig．8 Line chart of THD

3 结语

通过改造Haar小波的对偶小波函数获得按正弦规律变化的占空比函数，并基于对该占空比的跟踪实现了单相WM逆变器。由于采用占空比跟踪技术，信号的采样及重构频率与基波保持同步变化，因此逆变器输出电压谐波含量特别是基波附近的低次谐波含量降低。研究表明，逆变器输出电压频谱受采样组数D的影响，D较小时，宜根据Q*对占空比跟踪，D较大时，宜根据Q对占空比跟踪。

［1］张一博，王聪．NPC三电平光伏逆变器SVPWM合成和序列的优化［J］．电源学报，2012，40(2):72-75．ZHANG Yibo，WANG Cong．Synthesis and optimization of SVPWM for three-level NPC PV inverter［J］．Journal of Power Supply，2012，40(2):72-75．(in Chinese)

［2］孟超，欧阳红林，刘伟候，等．双Y移30°永磁同步电机的空间矢量调制［J］．中国电机工程学报，2010，30(3):90-99．MENG Chao，OUYANG Honglin，LIU Weihou，et al．Space-vector PWM techniques for dual Y shift 30 degree permanent-magnet synchronous motor［J］．Proceedings of the CSEE，2010，30(3):90-99．(in Chinese)

［3］Saleh A Saleh，Azizur Rahman M．Experimental performances of the single-phase wavelet modulation inverter［J］．IEEE Transactions on Industrial Electronics，2011，26(9):2650-2661．

［4］Saleh A Saleh，Cecilia R Moloney，Azizur Rahman M．Development and testing of wavelet modulation for single-phase inverters［J］．IEEE Transactions on Industrial Electronics，2009，56(7):2588-2599．

［5］Saleh A Saleh，Cecilia R Moloney，Azizur Rahman M．Analysis and development of wavelet modulation for three-phase voltagesource inverters［J］．IEEE Transactions on Industrial Electronics，2011，58(8):3330-3348．

［6］Saleh A Saleh，Azizur Rahman M．Optimal resolution level for input-output control of 3φ VS WM AC-DC converters［J］．IEEE Transactions on Industrial Electronics，2014，50(2):1432-1447．

［7］刘洪臣，刘雷，王云．小波调制逆变器电压调制比的理论分析［J］．哈尔滨工业大学学报，2013，45(10):63-68．LIU Hongchen，LIU Lei，WANG Yun．Analysis of inverters'voltage modulation ratio based on wavelet modulation［J］．Journal of Harbin Institute of Technology，2013，45(10):63-68．(in Chinese)

［8］刘雷．电力变换器小波调制策略研究［D］．哈尔滨:哈尔滨工业大学，2013．

［9］张金龙，漆汉宏，魏艳君．单相逆变器小波多分辨调制技术研究［J］．电力电子技术，2014，48(8):68-70．ZHANG Jinlong，QI Hanhong，WEI Yanjun．Research on single-phase inverter control tecbnolog based on multi-resolution wavelet modulation［J］．Power Electronics，2014，48(8):68-70．(in Chinese)