高等数学中的一些反例

尹建华，孟慧慧

（河北民族师范学院数学与计算机系，河北承德067000）

高等数学中的一些反例

尹建华，孟慧慧

（河北民族师范学院数学与计算机系，河北承德067000）

在高等数学中有一些命题或关系不成立，不需要理论证明，只需用一个反例即可说明。本文列举一些反例仅说明多元函数中不成立的命题和关系，同时也说明从一元函数到多元函数的性质也符合从量变到质变的原则。

连续；极限；偏导数；曲线积分

在高等数学中有许多概念，通过证明可以得到一些概念之间相互关系，但也有一些概念之间相互无关，这时只需举出反例说明即可。与之类似，定理成立要满足一定的条件，当条件不被满足时，结论若不成立也只需反例说明。下面通过反例说明高等数学中一些有关多元函数部分不成立的关系及结论。

1　与概念相关的反例

1.1二元极限，连续定义相关的反例

结论1：二元函数的极限不仅与函数、点有关，而且与定义域有关。

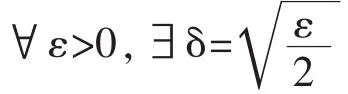
【结论2：多元函数连续与定义域有关。

证明：（1）在平面R2上，当沿(x,y)沿y=kx(k≠0)趋于(0,0)时，有，说明沿不同斜率的直线趋于原点(0,0)，对应极限值不同，极限不存在，所以f(x,y)在(0,0)不连续。

1.2关于极限关系反例

结论3：二重极限与累次极限的存在没有必然的联系.

当动点(x,y)沿抛物线y=x2趋于(0,0)时，有二重极限

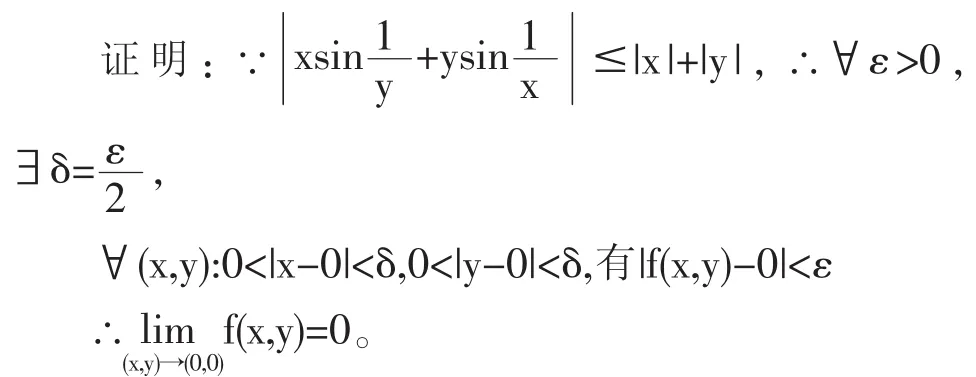
∴累次极限不存在，同理另一顺序累次极限也不存在。

结论4：沿任何方向的方向极限都存在，重极限也不一定存在。

1.3多元函数连续与一致连续关系反例

结论5：函数在某区间一致连续，则在该区间一定连续，但函数在某区间连续却不一定一致连续。

因此，函数f(x,y)在D非一致连续。

1.4多元函数可微、偏导存在、连续关系反例

一元函数中有关系：f(x)在某点可导充要条件是f(x)在该点可微；f(x)在某点可导，则f(x)在该点连续，但是f(x)在某点连续，却不一定在该点可导。从一元函数理论到多元函数的理论，也符合哲学道理，不仅有量的变化，而且有质的变化。

结论6：在多元函数理论中，可以证明结论：可微⇒偏导存在；可微⇒连续；其他关系都不具备。

【例7函数f(x)=｜x-3｜在x=3点连续但不可导。

∴f(x,y)在(0,0)点偏导数不存在。

1.5可微与方向导数关系反例

结论7函数在一点可微，则任何方向导数存在，反之不一定。点的方向导数及可微性。

解对于从原点出发的任何方向射线上l:y=kx上，都有充分小的一段包含在原点的某邻域U(O)内，在U(O)内有y=kx＞x2＞0或y=kx≤0，∴在这一段上f≡0，f(0,0)=0，，即在(0,0)点沿任何方向的方向导数都存在，但显然f(x,y)在(0,0)不连续，∴f(x,y)在(0,0)不可微。

2　与定理相关的反例

2.1偏导连续可与微关系定理反例

结论8定理条件只是充分条件，不是必要条件。

但是f(x,y)在(0,0)可微。事实上

由定义知f(x,y)在(0,0)可微。

2.2复合函数求导法则反例

定理若函数x=φ(s,t)，y=φ(s,t)在点(s,t)∈D偏导数存在，函数z=f(x,y)在点(x,y)可微，则复合函数z= f[φ(s,t),φ(s,t)]在(s,t)可微，且有

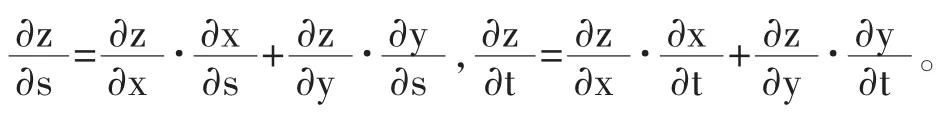
结论9若定理条件外函数f(x,y)不可微，公式不成立。

故定理条件外函数f(x,y)可微不可缺。

2.3有关格林公式反例

结论10函数在曲线围区域不连续，格林公式不成立。

根据题目所给条件，路线C可分为两种情况：

（1）C不经过原点,且原点不在以C为边界的区域D内。

这时P(x,y)，Q(x,y)满足定理条件，∴由格林公式

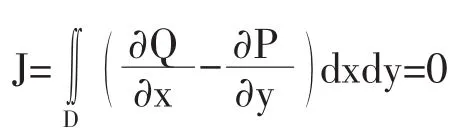
（2）C不经过原点，但原点在以C为边界的区域D内。

这时在（0,0）点，P(x,y)，Q(x,y)无意义（不连续），不满足格林公式条件，计算结果如下：以原点为心，充分小半径δ＞0为半径做元域D′：x2+y2≤δ2，其边界记C′，使D′完全含于D，则在环域D-D′内满足格林公式条件，C′为顺时针方向。由格林公式

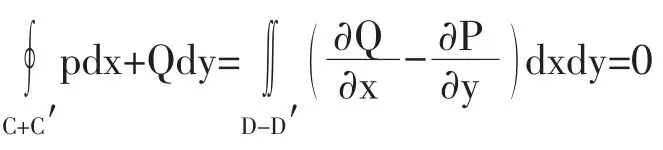
由二型积分计算公式

与格林公式计算结果不同，公式不成立。

2.4曲线积分与路线无关的反例

定理：设D是单连通闭区域，P(x,y),Q(x,y)在D具有一阶连续偏导，则有下列结论等价：（1）沿D内任何按段光滑封闭曲线C，有∮cPdx+Qdy=0；（2）对D内任一按段光滑曲线C，积分C∫Pdx+Qdy与路线无关，只与C的起点和终点有关；（3）Pdx+Qdy是D内某一函数u(x,y)的全微分；（4）在D内处处成立。

结论11：在曲线积分与路线无关的定理中，区域D必为单连通区域，否则结论不等价。

关于反例的作用不可轻视，它可以很快判定一个命题不成立。在其他学科仍存在这样的反例，如线性代数中矩阵乘法运算不满足交换律、消去律等。

On Counter Examples in Higher Mathematics

YIN Jian-hua,MENG Hui-hui
(Department of Mathematics and Computer Science,Hebei Normal University for Nationalities, Chengde,Hebei 067000,China)

Counter examples are preferred than theoretical argumentation in proving some false propositions or relational expressions in higher mathematics.Employing counter examples,this paper first illustrates some false propositions and relational expressions in multivariate function and then demonstrates that the properties from univariate function to multivariate function conform to the change from quantitative to qualitative.

continuity;limit;partial derivatives;line integral

O13

A

2095-3763（2015）02-0070-04

2014-12-10

尹建华（1963-），女，满族，河北隆化人，河北民族师范学院数学与计算机系教授。