三角形全等的判定方法探究

陈林

（江苏省新沂市高流初级中学，江苏 新沂 221411）

三角形全等的判定方法探究

陈林

（江苏省新沂市高流初级中学，江苏 新沂 221411）

在初中数学中，需要研究判定三角形全等的第一种方法——“SAS”。它能为判定三角形全等提供重要依据，并给进一步研究判定三角形全等的其他方法留下孕伏。因此，它在判定三角形全等中处于十分重要的位置。

初中数学；三角形全等；“SAS”

在初中数学中，需要研究判定三角形全等的第一种方法——“SAS”。它为判定三角形全等提供重要依据，并给进一步研究判定三角形全等的其他方法留下孕伏。因此，它在判定三角形全等中处于十分重要的位置。在多数初中数学教材版本中，都是通过学生画图、操作总结出“SAS”，并配备一定数量的练习题加以巩固和应用。针对教材弹性优点和学生的实际水平，笔者在探究“SAS”和部分练习题后，会再补充一道或两道开放题来进一步巩固“SAS”，以培养学生的观察分析图形能力和发散思维能力。依据新课标要求、教材内容和学生的认识能力和发展需要，笔者在教学这一内容时制定了如下教学目标：（1）学生能说出“SAS”，会用“SAS”证明两个三角形全等的简单问题。（2）培养学生动手操作、分析综合、合情推理和演绎等能力。（3）培养学生团结协作、严谨治学的思想品质，提高他们的自主参与意识，激发他们的学习兴趣和求知欲。笔者把“SAS”及其运用作为重点、“SAS”的发现和应用的书写要求作为难点。依据教材内容和学生认识规律，结合教学经验，笔者把教学过程分为三个部分：发现公理→明确公理→应用公理，五个环节：创设情境→发现公理→明确公理→应用公理→信息反馈。

学习这部分内容时，导入显得尤其重要。笔者是这样导入的：如图1，有一块三角形玻璃恰好碎成两块。如果要割一块与完好玻璃全等的玻璃，是否两块破碎玻璃都要带走？如果只需要带一块，那么带哪一块最适合？道理是什么呢？

图1

学生对这样的导入很感兴趣，他们议论纷纷，当他们粗略概括出“SAS”后，笔者让一位学生朗读课本上的有关内容，组织学生按照“画法”完成画图。接着，笔者要求完成画图的学生把△A’B’C’剪下，放在△ABC上，再要求任意两位学生把△A’B’C’叠合，观察它们是否全等。这样设计的意图是引导学生进行合理猜想，培养他们操作能力与合情推理能力，从而突破本部分内容教学的难点。

图2

为了明确公理，首先，笔者请一位学生朗读课本上的例子，笔者解释“S”“A”及“SAS”。其次，笔者采用竞答式组织学生完成课本上的相关练习题。最后，投影开放题。已知：如图2，点B、D、E在一条直线上，∠2=∠1。（1）如果△ABD≌△CBD，根据“SAS”，还必须加的一个条件是__=____。（2）如果△ABD≌△CBD，那么，△ADE≌△CDE吗？

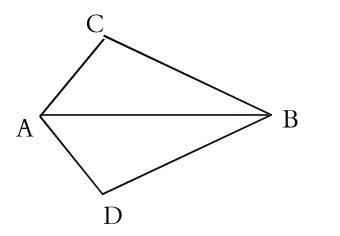
图3

题目出示后，让学生思考、讨论、竞答。这样设计的意图是让学生明确“SAS”，巩固“SAS”，从而突出教学重点。设计开放题也是为了培养学生的发散思维能力。为了让学生熟悉和应用公理，笔者投影例题：如图3，己知AC=AD，∠CAB=∠DAB，求证：△ACB≌△ADB。然后让学生观察图形并思考根据“SAS”能否推导出△ACB≌△ADB，若能，指出必备条件。同时，让学生自学课本上例题的证明过程。笔者说明，证明两个三角形全等的步骤：明确对象→摆齐条件→得出结论；关键：一是紧扣“SAS”找出相应条件，二要从图形出发弄清对应关系。笔者提问：同学们在图中还能发现其他相等的边（角）吗？为什么？学生思考、竞答。笔者又把图中△ADB绕AB中点旋转180O，得到如下变式图形（见图4）进一步巩固“SAS”。

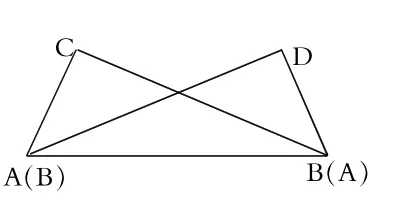
图4

在组织学生独立观察、思考并完成相关练习题的过程中，教师要给予学生适当的个别指导，通过例题教学培养学生观察、分析、归纳和综合问题的能力。同时，让学生会用边角边公理来证明，通过自学和老师指导使他们掌握证明的格式。在教学完这部分内容后，还要通过学生练习，考查他们应用“SAS”的情况。当然，还可以让学生对照教学目标，让他们谈谈自己的收获和疑难之处，鼓励他们大胆提问。在教学过程中，在让全体学生尽可能地完成本节课学习任务的同时，教师要适当地进行培优补差。

教学这部分内容，教学方法很关键。根据本节课的内容、学生的认知水平和笔者的教学经验，采用的教法主要有：自主探究法、指导自学法等。它们都属于启发式教学。

在教学这部分内容时，要选择带有情景性、发散性的内容，突出重点，化解难点。同时，采用“发现→明确→应用”的模式来完成教与学的任务。在完成本节课教与学的任务的同时，还需要注意前后知识的衔接，加强知识、能力、情感的综合培养。另外要注意这部分内容人文材料的挖掘，培养学生自主参与、自主探究的创新意识和创新精神，使学生享受数学的美感，领悟成功的体验。

[1]尚莉.培养高中生数学合情推理能力的实践研究[D].天津师范大学,2009.

[2]赵晓军.创设问题情境，引导学生主动获取新知[J].学生之友,2011（01）.

G633.6

A

1008-3561（2015）21-0093-01

陈林（1977－），女，江苏新沂人，中学一级教师，从事初中数学教学与研究。