试论一题多解巧解圆锥曲线的离心率

李立娟

（河北省唐山市曹妃甸区第一中学，河北 唐山 063299）

试论一题多解巧解圆锥曲线的离心率

李立娟

（河北省唐山市曹妃甸区第一中学，河北 唐山 063299）

圆锥曲线是高考必考部分，并且一直是一个热点和难点。通过2015年唐山市一模试卷的一道选择题，从不同的角度一题多解，代数问题几何化、几何问题代数化，两者有效结合，能提高学生分析问题和解决问题的能力。

双曲线；离心率；渐近线；向量

圆锥曲线是高考必考部分，大约试卷上有两道小题一道大题，基本上22分左右。离心率是圆锥曲线的重要性质之一，也是高考的热点问题。本文通过一道小题对圆锥曲线离心率的求法进行总结归纳，论述一题多解的优势。

2=3b2或b2=3a2，所以由，得e=2或者画图像（如图1）可得e=2时，AB两点在直线 的异侧，不符合条件2A→F→=F→→B，故舍掉。综上，

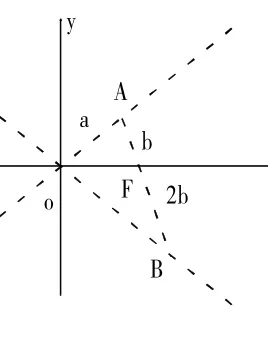
图1

点评：本解法主要考查双曲线的结论——焦点到渐近线的距离b，通过解方程得到点B的坐标，再找到b2与a2的关系，虽然易懂但计算量太大，较量费时间。

点评：方法同解法一，但得到点B的纵坐标后再利用长度的关系求解，计算量上大大减少，较上一种方法更简单易行。

点评：几何问题代数化，求交点，联立方程得到找到b2与a2的关系，与前两种解法相近，但要求计算能力较强。

点评：此解法也是先找出B的坐标，除了以上可以应用纵坐标找关系外，还可以利用横坐标建立等量关系，寻找答案。

点评：此法着眼于对图形的分析，抓住对称，还有|AF|=b，结合二倍角公式得到找到b2与a2的关系。此法较上两种方法更简单易行。

解法6：如图2，根据双曲线的对称性，过点F向双曲线的另一条渐近线作垂线垂足为C，易知|CF|=b，|BF|=2b，在Rt△ABC中，得∠FBC=30°，所以∠AOB=60°。在Rt△AOF中，得∠AOF=30°，所以

图2

点评：这种方法较以上几种方法有一种眼前一亮的感觉，数形结合解题简单易行，省时省力有效。

点评：此法是上一种方法的补充，充分利用教的关系以及渐近线的定义求解，很是巧妙。

小结：多角度思考问题，会开拓我们的思路，数形结合，将代数问题几何化、代数问题转几何，两者有效结合，我们会让抽象的题目变得有了生命。只有这样，才会使学生在考场上得心应手，取得优异的成绩。

[1]叶志祥，叶志根.巧解圆锥曲线离心率问题[J].中学生数学,2015(09).

[2]王荣鑫.妙用几何性质,巧解离心率范围[J].数理化学习,2013(12).

G633.6

A

1008-3561（2015）21-0065-01

李立娟（1976－），女，河北唐山人，中学一级教师，从事数学教学与研究。