对磨床电动机振动强度的探讨

陈 伟



对磨床电动机振动强度的探讨

陈 伟

（上海第三机床厂 上海201600）

介绍了磨床对振动强度的要求和电动机对振动强度的要求。论述了振动强度中振动位移、振动速度、振动加速度三种测量参数和峰值（O-P）、峰-峰值（P-P）、均方根值（r.m.s）三种幅值数据类型的相互关系以及换算方法。为解决电动机行业和磨床行业对电动机振动强度的不同测量参数间的换算提供了参考。

磨床 电动机 振动强度 单位换算

1 磨床的受迫振动

回转体由于其质量中心与回转中心存在一定的偏心距，由此产生转动时的离心惯性力，这种离心惯心力会造成回转体回转中心周期性的位移，这种周期性重复出现的振动现象属于一种受迫振动，按其运动规律也可称之为“简谐振动”。

在外圆磨床中，砂轮主轴由于零件尤其是砂轮的质量不平衡，在主轴高速旋转时就会造成主轴系统的受迫振动。传动砂轮主轴的电动机转子及其皮带轮的质量不平衡造成电动机转子的受迫振动，进而引起砂轮架的受迫振动。同理，工件主轴系统和传动工件的电动机转子、皮带轮系统也会因不平衡量引起受迫振动。

当砂轮主轴系统和工件主轴系统发生受迫振动，两主轴系统在轴线所在平面内形成相对的振动位移，这种周期性的砂轮相对工件的位移变化将会影响到工件表面的磨削质量[1]。

在上面所述的受迫振动中，由于砂轮转速一般比头架主轴转速高得多，砂轮架的振动是影响磨削质量的主要因素。而造成砂轮架受迫振动的主要因素是砂轮主轴系统的不平衡和电动机转轴系统的不平衡。磨床对电动机振动强度的要求是通过电动机制造商对电动机本身带半键进行振动测量、平衡校正和磨床行业对电动机装上皮带轮或联轴器后进行二次振动测量、平衡校正来实现的。本文主要讨论磨床和电动机对电动机振动强度的要求及其相互间的关系。

2 磨床对电动机振动强度的要求

各种类型磨床对电动机振动强度测量参数的选择是相同的，但是由于电动机安装部位和精度要求的不同对限值有所选择。

这里以外圆磨床为例，JB/T 7418.2-2007《外圆磨床第2部分：技术条件》给出的电动机振动强度要求见表1。

表1 电动机振动强度 单位（μm）

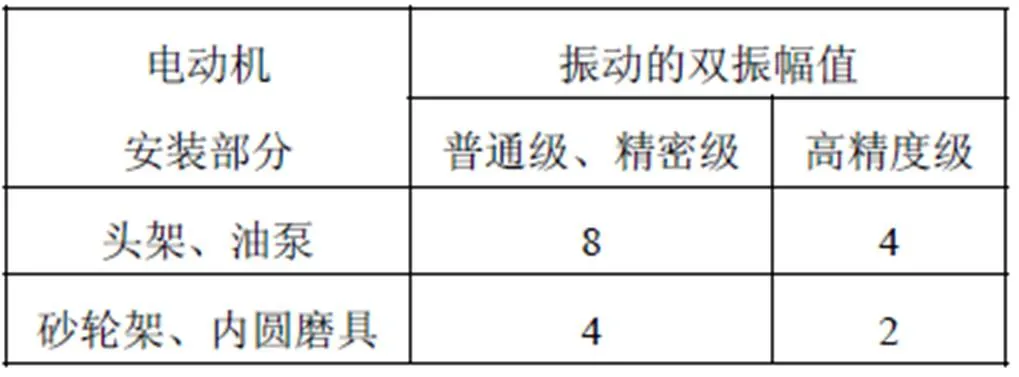
按标准要求，其测量振动和平衡校正时应包括皮带轮或联轴器。

由“振动的双振幅值”及其单位“μm”可以看出，这里给出的振动强度测量参数是“位移”。其次必须指出的是，在有关机械振动的国家标准和权威的技术手册中振动位移的测量参数里并没有“双振幅值”这一项；从字面上理解和从外圆磨床加工工艺的特点来看，这里对电动机振动强度所要求的“振动的双振幅值”应该是指振动强度的测量参数为“振动位移”，幅值的数据类型为“峰-峰值”。

3 电动机对振动强度的要求

电动机机械振动强度的测量评定和限值主要由国家强制性标准GB 10068-2008给予规定。该标准等同采用了国际电工委员会的IEC 60034-14：2007。（2008年6月19日发布，2009年6月1日实施）。该标准与2000年版比较，主要区别在于：

（1）对电动机振动强度的测量参数由之前的“振动速度”一项，调整为“振动位移、振动速度、振动加速度”三项，但该标准同时也规定转速在600 r/min~3 600 r/min的电动机检查试验时只检“振动速度”，另两项测量参数仅用于型式试验。

（2）电动机振动强度的等级由原来的N、R、S三级，调整为A、B两级。

GB 10068-2008对于轴中心高≥56 mm电动机的轴承座振动强度的限值见表2（仅以中心高H=56~132的电动机为例）。

表2 电动机的轴承座振动强度的限值表[2]

没有特别指出，电动机产品的机械振动强度均按A级制造交付；对于电机轴端带有键槽的电动机，测量振动和校正平衡时均用半键填充键槽。

特别需要强调的是，表2所列振动强度的限值数据类型均为“均方根值”（也称之为“有效值”），不是“峰-峰值”。

三相异步电动机常规产品的现行行业标准如JB/T 1091-2008（Y系列）、JB/T 8680-2008（Y2系列）、 JB/T 7127-2010 (YD系列)等在有关机械振动强度部分，前两项引用的还是GB 10068-2000，后者虽引用了GB 10068-2008但振动强度测量参数、幅值数据类型、限值等还是采用了GB 10068-2000。

也就是如果没有特别说明，电动机产品其振动强度通常是按“振动速度”A级（或N级）检验、交付的。

4 振动强度不同幅值数据类型间及测量参数间的关系

由前述可知，对于电动机机械振动强度测量参数的选择，磨床行业采用的是“振动位移”，电动机行业采用的是“振动速度”；对于电动机振动强度幅值数据类型的选择，磨床行业用的是“峰-峰值”，电动机行业用的是“均方根值”；这是由两个行业产品的特点决定的。

由于磨床行业与电动机行业对电动机振动强度采用了不同的测量参数和不同的幅值数据类型，这就造成了磨床行业与电动机行业在进行一些必要的换算之前，无法就电动机振动强度的大小直接进行交流和比较。不少技术人员也不清楚不同的振动强度测量参数间和不同的幅值数据类型间是否可以进行换算和如何进行换算。因此，常常会在电动机的采购、验收时产生一些麻烦。因此有必要来探讨一下其中的关系。

4.1 峰-峰值与均方根值的换算

作为一种简谐振动，振动幅值（即振幅，这里的振幅包括位移振幅、速度振幅、加速度振幅）中的峰值（O-P）、峰-峰值（P-P）、均方根值（r.m.s）之间存在如下关系[3]：

设峰值（O-P）为，则峰-峰值（）为：

A=2（1）

均方根值（）为：

由（1）、（2）消去可得：

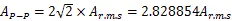
即由（3）、（4）式可知：

a) 均方根值是峰-峰值的0.3535倍；

b) 峰-峰值是均方根值的2.8289倍。

应用（3）式，将表1的外圆磨床电动机双振幅值（振动位移峰-峰值）转化为振动位移均方根值并与电动机的振动位移限值要求进行比较，见表3。

表3 电动机振动位移比较值

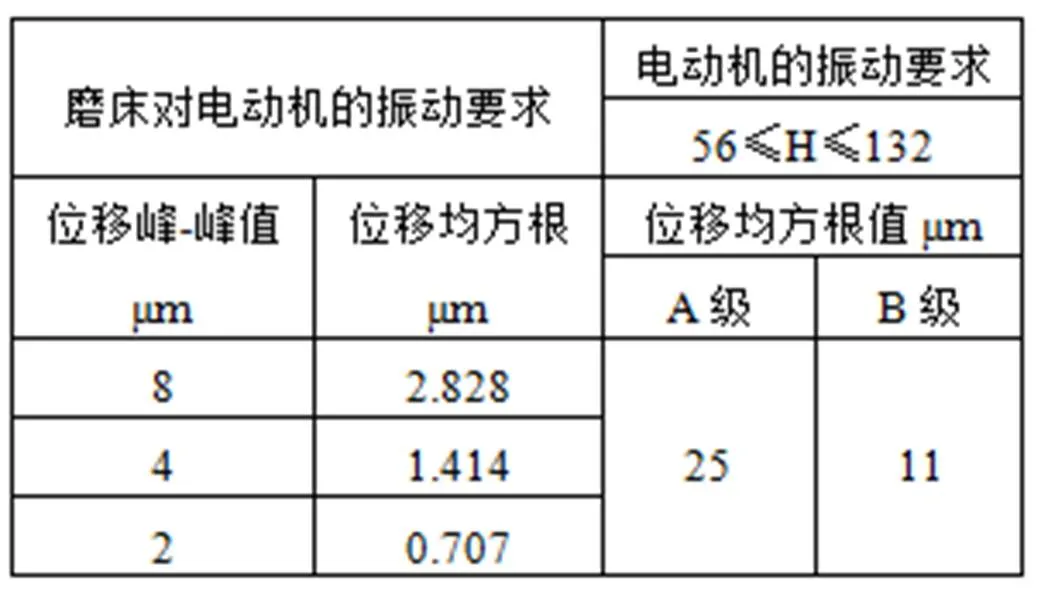
从表3比较可知，对振动位移的限值大小电动机本身的要求（按B级计算）是外圆磨床要求的约4~16倍，其精度远低于外圆磨床对电动机振动强度的要求。

4.2 振动强度测量参数间的换算

GB/T 6075.1-2012《机械振动在非旋转部件上测量评价机器的振动第1部分：总则》对振动的位移、速度、加速度三者之间的关系给出了如下的公式[4]：

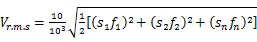
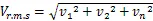
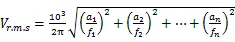
式中：s——振动的峰-峰位移值，μm；

v——振动的速度均方根值，（mm/s）；

a——振动的加速度均方根值，（m/s2）；

n——频率，（Hz）。

当仅对单一频率谐波分量进行振动位移、速度、加速度的变换时，则由(5)式可得位移峰-峰值转化成速度均方根值的关系式：

由式（8），可得速度均方根值转化为位移峰-峰值的关系式：

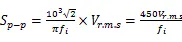
再由式（7）可得：

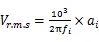
由（11）式，可得速度均方根值转化成加速度均方根值的关系式：

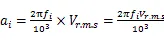
由式（10）、（12）可知：

对电动机而言，其频率（Hz）等于电动机的转速（r/min）除以时间60(s)。

由式（10），将表3中B级振动位移均方根值11 μm换算成振动速度均方根值，见表4；由式（10）将表3中B级振动速度均方根值0.7 mm/s换算成振动位移均方根值，见表5。

从表5比较可知，在电动机转速600 r/min时，对振动速度的限值大小电动机本身的要求也是外圆磨床要求的约4~16倍。随着电动机转速的增加（频率增加），这种差异就越来越小。

表4 电动机振动位移换算成振动速度

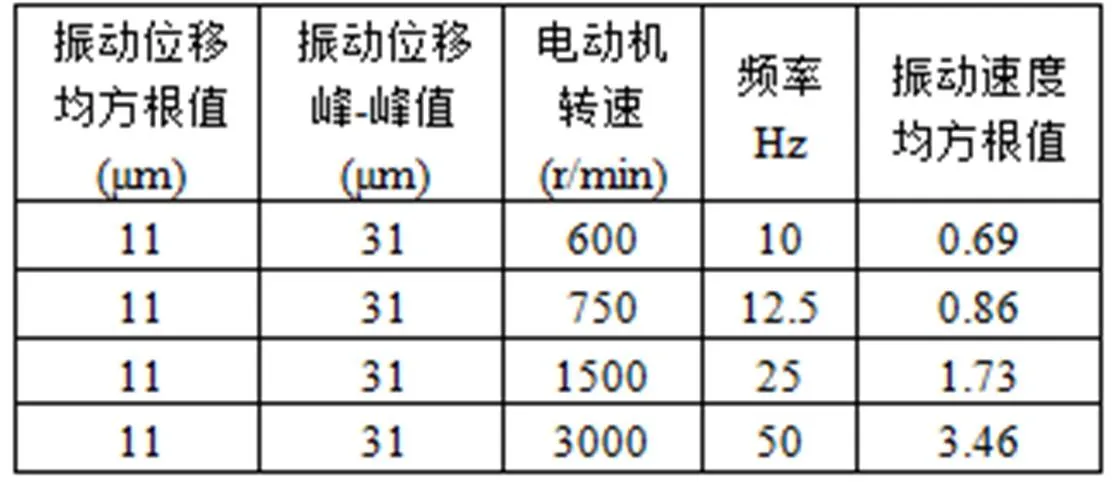
表5 电动机振动速度换算成振动位移

尽管振动位移、振动速度、振动加速度三个参数间可以进行换算，但这是在一个周期内对三个参数的幅值进行换算，这三个幅值不是发生在同一个时间点上的。在一个周期内速度与位移相位角相差π/2，加速度与位移相位角相差π。

5 结语

（1）对于同一个振动系统，振动位移与振动速度间换算时与一个常数及频率相关。当振动位移一定，则电动机转速越高换算成的振动速度越大（与频率正相关）；当振动速度一定，则电动机转速越高换算成的振动位移越小（与频率负相关）。

（2）与磨床主要电动机（如驱动砂轮、工件的电动机）相配的皮带轮或联轴器设计时应考虑允许在其表面通过去重校正轴系的不平衡量，以使电动机轴系振动强度小于磨床的要求。

（3）磨床的主要电动机应该在订货目录中注明对电动机半键平衡时振动强度的要求，明确振动强度测量参数类型和限值的数据类型。

（4）建议磨床类产品行业标准在修订时，能考虑规范对电动机振动强度的描述。应明确采用“振动位移峰-峰值”，并提供与“振动位移均方根值”、“振动速度均方根值”的换算方法，方便与电动机行业的技术交流。

[1] GB10068-2008轴中心高为56 mm及以上电机的机械振动、振动的测量、评定及限值[S].北京:中国标准化出版社,2008.

[2] GB/T 6075.1-2012机械振动在非旋转部件上测量评价机器的振动第1部分:总则[S].北京:中国标准化出版社,2012.

[3] 孙恭寿,汤锡铨.磨床精化与改造[M].北京:机械工业出版社,1986.

[4] 机械设计手册编委会.机械设计手册第5卷:机械设计基础[M].北京:机械工业出版社,2004.