基于幂律模型的数控机床可靠性评估

杨若霁



基于幂律模型的数控机床可靠性评估

杨若霁

（上海机床厂有限公司 上海200093）

基于幂律模型对数控机床可靠性进行评估，并与采用威布尔模型计算得到的可靠性指标进行比较，结果表明：数控机床故障间隔时间非独立同分布，并呈明显增大趋势，由幂律模型得到的累计MTBF点估计值是动态值，随累计故障强度的减小而增大，与MTBF观测值基本一致，而威布尔模型MTBF点估计值比MTBF观测值低很多。因此，在故障间隔时间非独立同分布的情况下，幂律模型较威布尔模型更能准确地评估数控机床可靠性，并可预测下一个设备工作时间点的MTBF值。

幂律模型 数控机床 可靠性 MTBF

数控机床作为现代制造业的重要装备，其可靠性指标是衡量一个国家机床制造水平的重要标志。长期以来，对于数控机床可靠性评估技术一直是国内外学者的研究热点之一。

在数控机床可靠性评估中，传统可靠性评估模型，如指数分布、正态分布和威布尔分布模型等，都假定故障间隔时间独立同分布，即故障间隔时间相互独立且来自同一母体。但数控机床是集机、电、液、光于一体的复杂可修系统，故障修复时间相对于工作时间一般很小，特别当故障间隔时间非独立同分布并呈现明显增大或减小趋势时，传统分布模型得到的MTBF估计值将与MTBF观测值产生较大偏差。

幂律模型较传统可靠性模型更适用于故障间隔时间非独立同分布的情况[1]，这里运用该模型对某系列2台数控机床可靠性进行评估。

1 幂律模型

1.1 模型理论

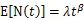
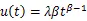
1.2 模型参数估计

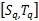
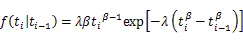
所以，故障时间在区间[，]的似然函数为：

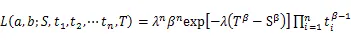
由此k台机床的对数似然函数为：

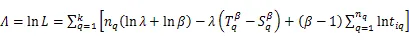
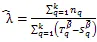
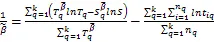
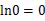
式（6）为估计值的非封闭形，可先用迭代法解出，随后再求出的估计值。

1.3 模型参数与可靠性指标的区间估计

由于极大似然估计量渐进正态分布，因此参数θ的估计区间值为：

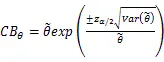
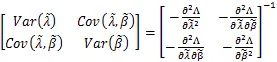
由幂律模型推得的累积平均无故障间隔时间(MTBF)的函数表达式[4]为：

累积故障强度的函数表达式为：

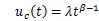
式（9）、（10）的方差表达式分别为：

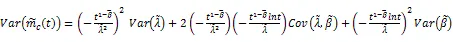
（12）

上式中的为设备工作时间。由式（7）～（12），可得到可靠性指标的区间估计。

1.4 模型检验

零假设H0：故障间隔时间独立同分布；备选假设H1：故障间隔时间为具有单调强度函数的非齐次泊松过程。检验统计量在零假设下，渐进于正态分布[5]。对于多台系统，其检验统计量为：

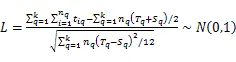
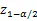
2 数控机床可靠性评估实例

以某系列2台数控机床在[0，1894]统计时间内的现场故障数据为例进行可靠性评估，其发生故障时间如表1所示。

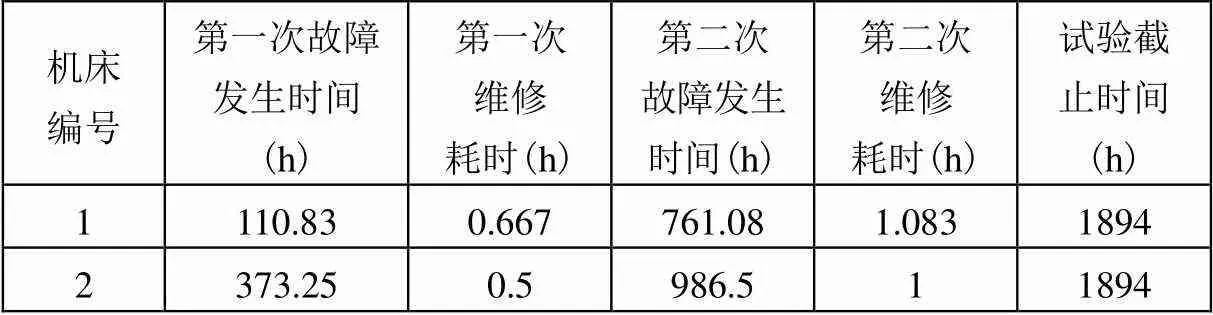
表1 数控机床故障数据

图1、图2分别为累计故障强度与累计MTBF的时间趋势图。

图1 幂律模型—累计故障强度时间趋势图

图2 幂律模型—累计MTBF时间趋势图

若取统计结束时间，则累计故障强度的点估计值为0.0011，累计MTBF的点估计值为947h。

由式（8）得到参数协方差矩阵：

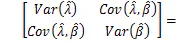
代入式（11）、（12），得：

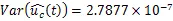
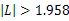
3 比较与分析

如表2所示，将两台机床的时间点列出，最后一个时间点为试验截止时间，比较威布尔模型MTBF点估计值、幂律模型累计MTBF点估计值与MTBF观测值，其中威布尔模型MTBF点估计值由机床故障间隔时间和截尾时间计算得到[6]，MTBF观测值是由机床总工作时间与总故障次数计算得到（该值为标称值）[7]。

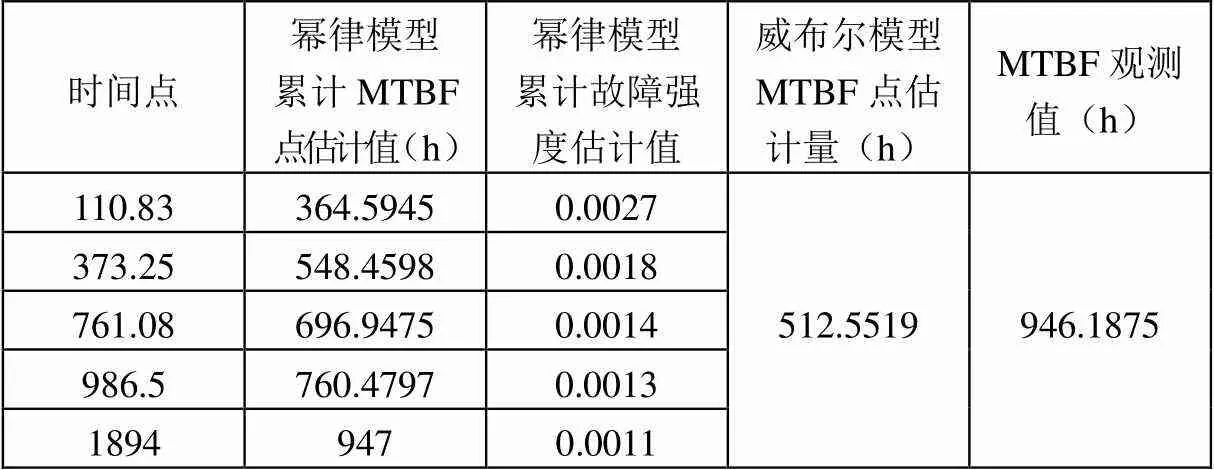
表2 MTBF评估结果比较

从表2可知：幂律模型累计MTBF点估计值是动态值，随累计故障强度的减小而增大，具有趋势性，可预测下一个设备工作时间点的平均故障间隔时间（见图2）；威布尔模型MTBF点估计值为平均值，无趋势性。

此外，威布尔模型MTBF点估计值比MTBF观测值低很多，而幂律模型在试验截止时间的MTBF点估计值与MTBF观测值基本一致，其原因在于：两台机床的故障间隔时间非独立同分布，导致威布尔模型计算得到的可靠性指标估计值与标称值之间产生较大偏差。

4 结语

采用幂律模型对2台数控机床现场故障数据进行分析，并与采用威布尔模型计算得到的数据进行比较，结果表明：数控机床故障间隔时间非独立同分布，并呈明显增大趋势，由幂律模型得到的累计MTBF点估计值是动态值，随累计故障强度的减小而增大，与MTBF观测值基本一致，而威布尔模型MTBF点估计值比MTBF观测值低很多。

因此，在故障间隔时间非独立同分布的情况下，幂律模型较威布尔模型更能准确地评估数控机床可靠性，并可预测下一个设备工作时间点的MTBF值。

[1] 王智明.数控机床的可靠性评估与不完全预防维修及其应用[D].上海:交通大学,2011.

[2] Crow L H. Confidence interval procedures for the Weibull process with applications to reliability growth[J]. Technometrics, 1982,24(1):67-72.

[3] Crow L H. Evaluating the reliability of repairable systems[C].IEEE Proceedings Annual Reliability and Maintainability Symposium,1990:275-279.

[4] Charles E Ebeling.可靠性与维修性工程概论[M].北京:清华大学出版社,2010.

[5] Louit D M, Pascual R, Jardine A K S. A practical procedure for the selection of time-to-failure models based on the assessment of trends in maintenance data[J]. Reliability Engineering and System Safety,2009, 94(10):1618-1628.

[6] 李慧亮.基于威布尔分布的数控机床可靠性分析[J].机床与液压,2014,42(19):191-194.

[7] 肖俊.数控机床可靠性技术的分析与研究[D].上海:交通大学,2007.