高中数学解题中“巧”的魅力

陈金铭

【摘 要】高中数学是高中教育课程体系中的重要组成部分，它经常被视为难度系数最高的一门学科，在解题过程中，学生经常会出现无从下手的现象。在实际教学过程中，我们不难发现，对高中数学进行“巧”解，不仅能加快解题速度，而且能为解题提供一个全新的思路。本文从具体实例出发，详细介绍高中数学解题中“巧”的魅力，从而达到提高整体高中数学教学质量的目的。

【关键词】高中数学      解题     “巧”解

当今教育话题成为全民探讨的热门话题。无论是各大影视广受关注，还是不同教育学校相继建成，都表达了人们对教育事业的重视程度。随着我国对素质教育的推行，对教育的改革力度也正在逐步加强。高中数学作为教育事业的重中之重，它的教学成果显得尤为重要。它不仅直接关系着学生高考的成绩，更与人们在日常生活中的实际应用密不可分。然而，高中数学并不等同于小学、初中数学，其题型往往更加复杂、解题过程更加烦琐。要想实现解题中“巧”的效果，则应从数学概念、题目信息、解题思路三方面着手。

一、明确数学概念，寻找“巧”解方法

要想实现高效解题，则必须对数学知识做到全面掌握。高中数学概念同样包含其中，不仅要做到全面理解，还要学会灵活运用。在很多高中数学解题中，从最基础的数学概念入手，往往可以取得意想不到的突破，最大限度地提高解题效率。

实例一：已知tanα=，求（cosα+sinα）/（cosα-sinα）的值。该题属于常见的三角函数题型，是有关正弦函数、余弦函数、正切函数之间的数学知识点。在常规解题过程中，学生经常会被外部形式给难倒，忽略了它们三者之间的内部关系，从而导致解答很久都无法算出正确结果。所以，我们要从概念着手，分析它们的内部联系，对其概念进行很好的利用。在三角函数中，正切值等于正弦值与余弦值的商，即tanα=sinα/cosα，再联系sin2α+cos2α=1，可以将（cosα+sinα）/（cosα-sinα）可以转化成（1+sinα/cosα）/（1-sinα/cosα），即所求函数式可以表示为（cosα+sinα）/（cosα-sinα）=（1+sinα/cosα）/（1-sinα/cosα）=（1+tanα）/（1-tanα）=（1+）/（1-）=-3-2，最后得出结果。对数学概念的巧妙运用，使解题思路更加清晰化，推理过程准确无误，运算量大大减少。

二、分析题设信息，获取“巧”解途径

在数学学习过程中，我们经常看到很多学生死记公式以便在加快解题效率，但是常常会出现乱用公式、错用公式的现象。究其原因，就是忽略了对题目信息的审核，缺乏一定的严谨性，从而掉进了题设“陷阱”当中。所以，在解答数学题时，一定要避免机械化的学习，要做到对信息内容的分析，从而使题目迎刃而解。

三、“巧”用数形结合法，变换解题思路

在数学解题过程中，数形结合法是一种必不可少的解题策略，该思路能将看起来较为复杂的数学题目更加直观形象地表达出来，一定程度上提高了解题时的理解能力，化繁为简、化难为易，为“巧”解题目奠定了良好的基础。关于这一新思想，早在很多年前，华罗庚也对其进行了肯定。这一方法的具体应用，可以通过实例二表示出来。

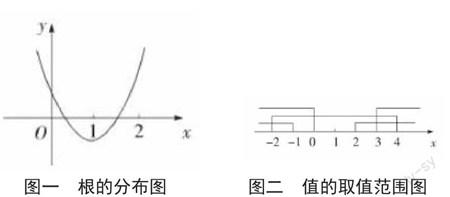
实例二：已知方程6x2-（m+11）x+m2-m=0的两个实根x1、x2满足00，f（1）<0，f（2）>0。用数据表达为m2-m>0，m2-2m-5<0，m2-3m+2>0，得出最后结果-2

图一  根的分布图         图二  值的取值范围图

通过图象观察，我们不仅可以在解题前对题目有更深层次的理解，还可以对其结果有更直观地了解。数形之间达到巧妙的结合统一，可以让学生在学习过程中更加轻松，有效提高了学生的创新思维，为学生的数学解题思路开拓了一个新的途径，对他们的能力提高有促进作用。

四、结束语

总体来说，在高中数学解题时，“巧”的魅力体现在方方面面，有效应用“巧”解策略可以达到提高数学成绩的良好效果。对于学生而言，在解题过程中，要积极努力寻找“巧”的魅力所在，敢于突破常规思维，从多重理解上进行解题。对于老师而言，在教学过程中，要注重培养学生“巧”解数学的能力，使其技能得到提高，并且要将“巧”解思想应用到具体实践中去，加大对学生该能力的培训力度，使学生运用自如。作为一种新型解题策略，“巧”解魅力发挥着持久不散的作用，它在整个教学领域中都应该得到推广，而不仅仅只是对高中数学而言。只有将其应用到每一门课程的教学之中，才能使学生更加全面发展，提高学生的综合能力，从而提高整体教学水平，为我国的教育事业发展起到推波助澜的作用。

【参考文献】

[1]杨子清，温培珠.初中数学解题方法与技巧教学的研究[C].中华教育理论与实践科研论文成果选编（第三卷），2012，32（11）：489-490.

[2]郑亚军，张雪萍，祁美萍.数学解题常见错误例析[C].萃英集——青海省教育委员会、青海省教育学会优秀教育论文集，2012，20（09）：667-668.

[3]苏少卿，钱斌，冯红果.中学生数学解题效率成因研究[C].全国高师会数学教育研究会2006年学术年会论文集，2012，30（03）：603-604.