基于角速率与角增量的捷联惯导姿态算法
尹剑,邓宏林,杨萌,张琬琳
(西安应用光学研究所,西安710065)
基于角速率与角增量的捷联惯导姿态算法
尹剑,邓宏林,杨萌,张琬琳
(西安应用光学研究所,西安710065)
对于捷联惯性姿态计算来说,目前存在着多种算法。这些算法如何归类、区分、如何在进行算法设计时根据具体应用进行算法选择,很容易给设计者造成困扰。针对这个问题,根据姿态算法所采用的角速率和角增量的采样方式,配合四元数算法和方向余弦算法,采用仿真手段,对常用的捷联姿态计算进行了归纳和分析比较,给设计捷联姿态算法提供了参考。
捷联惯性导航;姿态计算;角速度;角增量
随着捷联惯性技术的发展,新型陀螺仪如激光陀螺和光纤陀螺等已经成功地得到了应用,陀螺仪的输出形式也不仅仅限于传统的角速率输出[1-5]。目前常用的输出形式有2种,一种是角速率输出,也就是每次采样输出的值是当前时刻的角速率,即陀螺敏感轴感知的机体坐标系下该坐标轴相对于惯性坐标系的角速率ωib;另一种是陀螺输出时将采样周期Δt内的角速率进行了积分,从而输出了采样间隔周期内的角增量,即。根据这2种不同的采样方式,在进行捷联姿态计算时,相应的姿态算法也有所不同[6-8]。通常而言,对于角速率采样,采用直接求解姿态更新微分方程的方法,工程上常用四阶龙格库塔法实现。对于该算法,根据姿态计算使用的参数的不同,又分为四参数的四元数龙格库塔法和九参数的方向余弦龙格库塔法;对于角增量采样,一般采用求解姿态微分方程的解析算法,同样,根据姿态计算使用的参数的不同,分为四参数的四元数必卡逼近法,根据采样数目不同又细分为四元数等效旋转矢量的单子样、双子样、三、四子样等多子样算法以及九参数的方向余弦算法,以及方向余弦的单子样、双子样及多子样算法[9-10]。下面将对基于角速率和基于角增量的上述算法进行简要的分析比较。
1 角速度采样姿态算法
采用角速率采样的捷联姿态算法常用的有四元数法和方向余弦法。对于这2种算法,由于角速率采样的值是姿态微分方程的计算参数,因此通常采用直接进行微分方程求解的计算方法,龙格库塔法是工程上经常使用的方法。龙格库塔法根据泰勒级数展开的误差项阶数不同可以分为一阶、二阶、三阶、四阶等等,工程上需要综合考虑实现的难度及精度,四阶龙格库塔法比较常用。
1.1 方向余弦四阶龙格库塔法
方向余弦姿态更新微分方程为
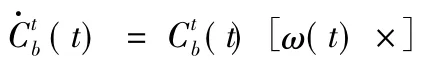

其中,ωx(t)、ωy(t)、ωz(t)分别为载体旋转角速度t时刻时在载体坐标系X、Y和Z轴的分量,则利用四阶龙格库塔法的计算方法,在采样周期为T的时间间隔内,按照如下分解步骤进行计算:

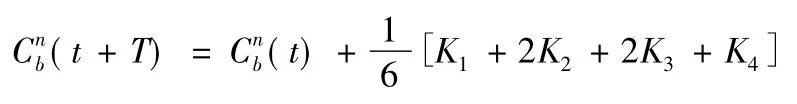
1.2 四元数的四阶龙格库塔法
四元数微分方程的形式为

式中:Q(t)为t时刻的姿态四元数值;
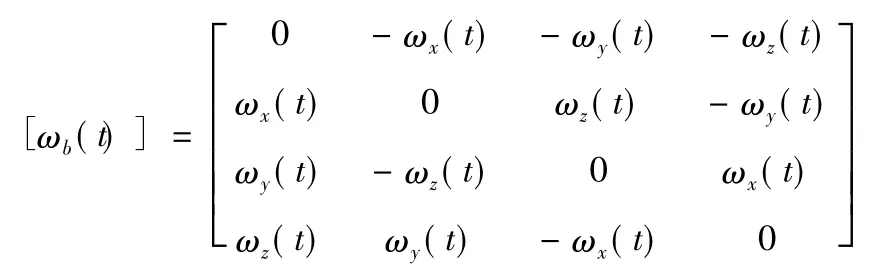
ωx(t)、ωy(t)、ωz(t)分别为飞行器旋转角速度t时刻时在载体坐标系X、Y和Z轴的分量。利用四阶龙格库塔法的计算方法,在采样周期为T的时间间隔内,按照如下分解步骤进行计算:
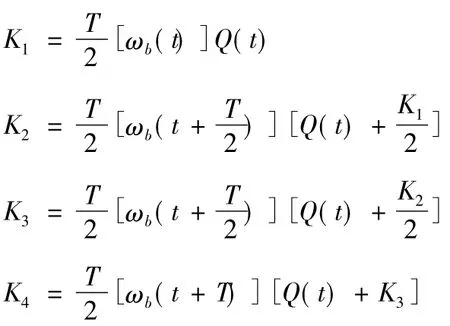
则更新后的四元数姿态值Q(t+T)为
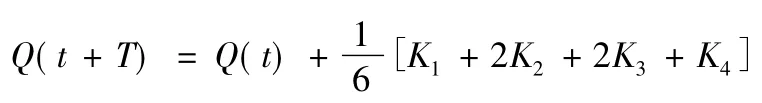
2 角增量采样姿态算法
对于陀螺输出为角增量时,通常采用解姿态更新微分方程的方法,由于微分方程的解中含有角增量成方,因此在姿态更新时,可以直接采用角增量进行计算,简化了计算流程并减少了误差。常用的角增量姿态算法有方向余弦法和四元数法。
2.1 方向余弦角增量采样姿态算法
采用角增量采样时,方向余弦微分方程的解为

2.2 四元数角增量采样毕卡逼近算法
四元数微分方程的解为
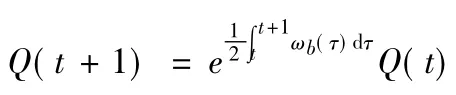
采用毕卡逼近法,四元数微分方程的解可以表示为

其中角增量计算式为

3 仿真分析
利用仿真的手段,对上述2种算法从精度方面进行分析,采用对捷联惯性姿态运算来说最恶劣的工作环境条件:圆锥运动进行仿真。仿真圆锥运动的半锥角为1°,圆锥运动频率为2 Hz,计算周期数为600点,计算频率均为100 Hz。
仿真比较一:在上述相同的仿真条件下,比较方向余弦法与四元数法在速率采样和角增量采样时算法结果在精度方面的差异。图1为采用方向余弦角速率采样的四阶龙格库塔算法的航向角H、俯仰角φ、横滚角θ误差;图2为采用四元数角速率采样的四阶龙格库塔算法的航向角H、俯仰角φ、横滚角θ误差。
由上述仿真结果可见,方向余弦算法和四元数算法在使用角速率采样的四阶龙格库塔算法时,在计算精度方面差别非常小,并且误差变化趋势相似。角速率算法误差统计结果如表1所示,同样的,在上述仿真条件下,采用每个计算周期采样一次的单子样角增量算法误差统计结果如表2所示。

图1 方向余弦四阶龙格库塔法姿态误差
四元数四阶龙格库塔算法的航向角H、俯仰角φ、横滚角θ误差如图2所示。

图2 四元数四阶龙格库塔法姿态误差
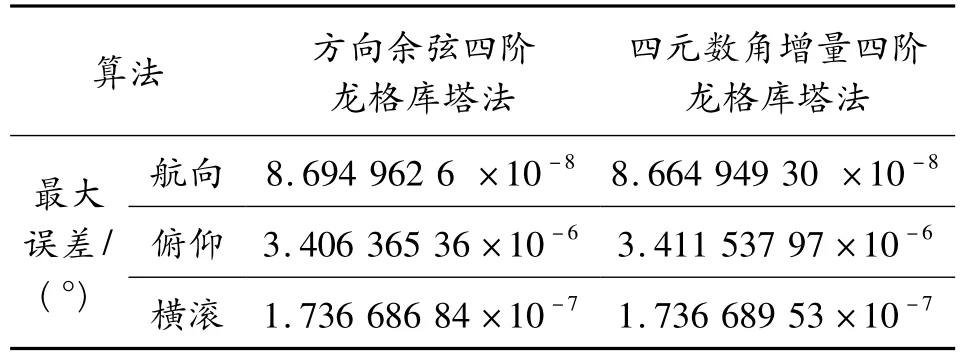
表1 角速率算法误差比较
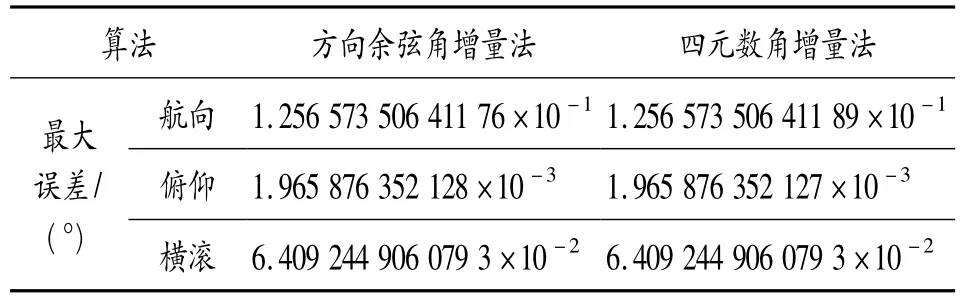
表2 角增量算法误差比较
由表1、表2对比可以发现在相同的圆锥运动的情况下,角增量算法精度比角速率精度高几个数量级。分析龙格库塔算法可知,龙格库塔法在进行计算时,在一个计算周期内利用了2次采样数据,因此龙格库塔算法实质上是一种双子样算法。下述仿真方法二将对采样2次的角速率龙格库塔法与角增量双子样算法进行比较。
仿真方法二:仍然采用上述圆锥运动方式,对角速率与角增量的算法精度进行比较。为了在采样间隔上与角速率算法一致,角增量算法采用在一个计算周期内使用2次采样值的双子样采样算法,仿真方向余弦双子样算法姿态误差如图3所示,四元数双子样算法姿态误差如图4所示。
综合上述仿真结果对方向余弦的角增量双子样算法和角速率四阶龙格库塔法以及四元数的角增量双子样算法与角速率的四阶龙格库塔法进行姿态误差比较如表3所示。
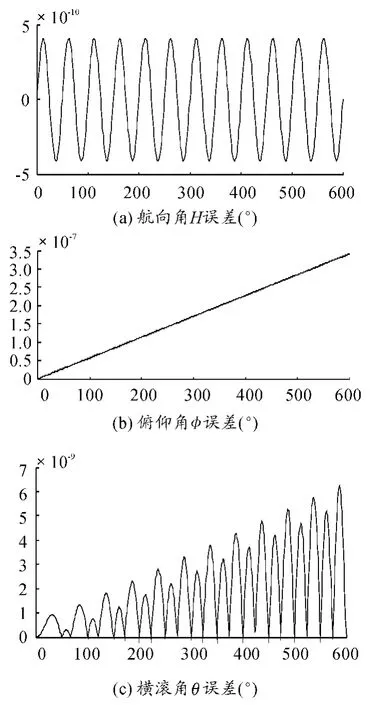
图3 方向余弦双子样算法姿态误差
很容易看出无论是角增量算法还是角速率算法,方向余弦法与四元数法精度相当,双子样算法精度高于单子样算法。而且,在同样采用一个计算周期内利用2次采样值进行姿态计算时,角增量算法精度高于角速率算法精度,这是由于陀螺输出角增量比输出角速率更好地保存了传感器的实时信息,即瞬间动态特征,因而给出了更精确的测量结果,所以提高了姿态计算的精度。

图4 四元数双子样算法姿态误差

表3 算法误差比较
4 结论
通过对比角速率采样算法和角增量采样姿态算法具体过程及计算姿态误差仿真可以得到以下结论:
1)角速率采样算法具有直观、容易理解的特点,而角增量算法需要求解姿态微分方程,因此形式相对复杂。
2)无论采用角速率还是角增量采样,捷联姿态计算的2种常用算法方向余弦法与四元数法的计算精度相当,且误差值的变化趋势相似。
3)在相同的采样时间间隔内,采用角增量姿态算法比采用角速率姿态算法的精度要高,这是由于角增量采样较好地保存了陀螺传感器的测量信息。
4)在一个计算周期内采样2次比采样一次算法的计算精度高,这是因为采样次数越多,越能克服惯性姿态计算中的不可交换误差,从而提高了姿态计算精度。
[1]秦永元.惯性导航[M].西安:西北工业大学出版社,2006.
[2]胡小平.自主导航理论与应用[M].长沙:国防科技大学出版社,2002.
[3]邓正隆.惯性技术[M].哈尔滨:哈尔滨工业大学出版社,2006:140-180.
[4]杨培根,龚智炳.光电惯性技术[M].北京:兵器工业出版社.1999:195-199.
[5]高伯龙,李树棠.激光陀螺[M].长沙:国防科技大学出版社,1984.
[6]郭来军,彭书家,白洪梅,等.弹载惯性测量单元检测系统的设计与实现[J].四川兵工学报,2014(4):15-18.
[7]张琬琳,尹剑,郭栓运.Q-MEMS陀螺零偏补偿技术研究[J].应用光学,2010,7(4):549-552.
[8]倪兴,李晓勇,薛国虎,等.测量船姿态误差影响分析[J].四川兵工学报,2014(5):149-151.
[9]Savage P G.Strapdown inertial navigation integration algorithm design,Part 1:attitude algorithms[J].Journal of Guidance Control and Dynamics,1998,21(1):19-28.
[10]Lee J G,Park C G,Park H W.Multiposition alignment of strapdown inertial navigation system[J].IEEE Transactions on Aerospace and Electronic Systems,1993,29(4):306 -311.
(责任编辑杨继森)
Strapdown Inertial Navigation Attitude Algorithm Based on Angle Velocity and Angle Increment
YIN Jian,DENG Hong-lin,YANG Meng,ZHANG Wan-lin
(Xi'an Institute of Applied Optics,Xi'an 710065,China)
There are many algorithms in strapdown inertial navigation attitude calculation field.But it always puzzled the designers about how to classify them and how to select appropriate attitude algorithm.To solve this problem,some widely used attitude algorithms such as quaternion method and direction cosine matrix method were classified based on angle velocity sampling and angle increment sampling.Analysis and comparison of these algorithms were presented by simulation method.
strapdown inertial navigation;attitude algorithm;angle velocity;angle increment
尹剑,邓宏林,杨萌,等.基于角速率与角增量的捷联惯导姿态算法[J].四川兵工学报,2015(11):101 -104.
format:YIN Jian,DENG Hong-lin,YANG Meng,et al.Strapdown Inertial Navigation Attitude Algorithm Based on Angle Velocity and Angle Increment[J].Journal of Sichuan Ordnance,2015(11):101-104.
U666.12
A
1006-0707(2015)11-0101-05
10.11809/scbgxb2015.11.027
2015-06-09
尹剑(1972—),男,博士研究生,高级工程师,主要从事光电定位定向技术研究。

