动态目标的电磁散射模型

周城宏，钱卫平，郭永强

（北京跟踪与通信技术研究所空间目标测量重点实验室，北京100094）

动态目标的电磁散射模型

周城宏，钱卫平，郭永强

（北京跟踪与通信技术研究所空间目标测量重点实验室，北京100094）

雷达静态目标的电磁散射特性可用成熟的电磁计算方法精确求解，动态目标则需在准静态原理假设下近似计算；基于Maxwell方程组和入射电磁场边界条件在雷达参考系和目标参考系相互转换规律，在目标参考系中构建了动态电磁散射问题的精确数学形式——非均匀边界条件下的Maxwell方程求解问题；随后讨论了准静态近似的理论依据，指出其适用范围局限于非相对论速度的动态目标。

刚体运动；电磁散射；参考系转换；准静态原理

电磁散射［1-3］是散射体被电磁波照射产生等效激励源并在空间场点激发散射电磁场的过程，其数学本质是在入射电磁场边界条件和介质本构方程约束条件下对Maxwell方程求解。电磁散射是研究目标散射特性的成熟理论，一般问题可用矩量法、有限元法和时域有限差分法等通用电磁计算方法精确求解。对于雷达目标而言，其散射特性决定于目标的几何形状与结构、材料组成与分布、运动状态与姿态，以及入射电磁波的频率和极化等特征［1］。为抽象出主要特征，通常将雷达目标散射场景简化为静态目标的单频平面电磁波照射，散射体与谐振电磁场构成了稳态系统。动态目标由于姿态的连续变化，激励源与散射场均随时间变化，系统处于非平衡态。为此可采用多个不同静止姿态场景将运动状态离散的方式对非稳态电磁散射进行刻画，其基本假设是准静态原理，即将动态目标的电磁散射强度近似等于当前姿态下静止目标的散射强度，以多个静态序列近似表征动态情形。

准静态近似具有一定的合理性［4］，可从目标电磁散射弛豫时间的角度定性分析，如何从电磁散射基本原理出发刻画其数学本质却值得深入研究，需先对动态目标的电磁散射问题进行精确刻画。在雷达系中，目标的时变状态使得激励源与散射场随之变化，非平衡态散射系统无法以简便的形式精确表征。如果基于Maxwell方程组和入射电磁场边界条件在雷达参考系和目标参考系相互转换规律，将散射问题从雷达参考系转换到目标参考系，则动态目标电磁散射问题转化成了时变入射边界条件的静态目标散射问题，再将该问题的解逆变换回雷达参考系即为最终解。立足于如上出发点，本文提出了基于参考系变换的动态目标电磁散射模型，给出了目标参考系中的电磁散射问题的数学形式，并揭示了准静态近似的数学合理性。

1 基于参考系变换的电磁散射模型

雷达参考系中动态目标电磁散射问题只能在准静态原理下近似求解，若将其变换到目标参考系中，理论上可以得到散射问题解的精确形式。

1.1 散射问题的参考系变换

电磁散射过程可视为一个散射体对入射电磁场边界条件的响应，可记为EMScattering，系统输入为入射电磁场（Ei，Hi），系统输出为散射电磁场（Es，Hs），则该过程可表示为

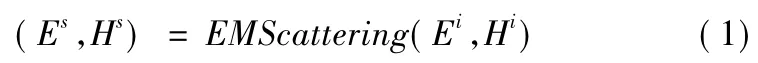
（Ei，Hi）在雷达参考系和目标参考系分别记为，相应地散射场记为，若雷达系向目标系的参考系变换记为Trans，Trans-1表示目标系向雷达系的变换［5］，则

式（2）可表示为以下过程图（图1）：

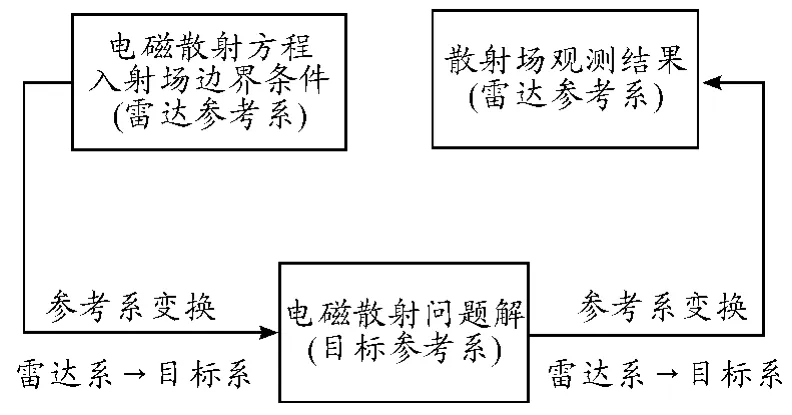
图1 散射问题的参考系变换

散射问题的方程、边界条件和解的变换，均可表示为电磁场在雷达系与目标系之间的相互转换。刚体目标的运动分为平动和转动，与之相应的目标系相对雷达系而言分别为平动参考系和转动参考系。在给定时刻t，瞬时平动参考系为惯性参考系，电磁场从雷达系向目标系的转换满足洛伦兹变换，瞬时转动参考系为匀速转动参考系，电磁场转换满足旋转洛伦兹变换，对目标给定参考点，旋转洛伦兹变换等效为洛伦兹变换。

1.2 目标参考系电磁散射

在目标系中，电磁场遵循基本电磁规律，用Maxwell方程组和各向同性介质本构方程D=εE，B=μH，J=σE表征，其中，ε、μ和σ分别表示介质的介电常数、磁导率和电导率，在已知入射电磁场边界条件的情况下，可对本构介质约束下的偏微分方程组进行求解：

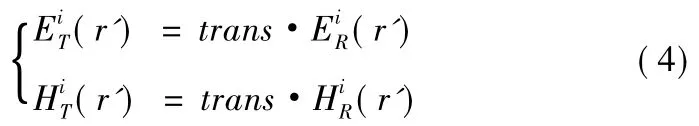
对于一般空间目标探测场景，雷达照射的电磁波以单频平面电磁波表征。因此，雷达系中入射电磁场在空间均匀分布，频率fc唯一。波在相对运动不同参考系下观测结果不同，即呈现多普勒效应，雷达照射电磁波的频率调制满足电磁场在不同瞬时参考系间的洛伦兹变换［6］。若散射微元r'的雷达视向速度为v（r'），在与散射微元r'相对静止的惯性参考系中，接收到的雷达照射频率满足

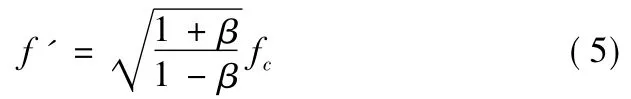
其中，β=v/c。因此，若空间目标各散射元的视向速度不同，则在目标参考系中接收到的电磁场的频率不再唯一，呈现与散射元雷达视向速度相关的分布；若目标相对雷达只有平动，则各部分的入射边界条件仍旧为均匀分布，照射电磁波的频率为f'。利用电磁散射解析或数值方法可以对目标参考系中非均匀边界条件的偏微分方程组进行求解。

1.3 散射场的逆变换

在目标参考系下对散射问题求解获得空间散射场后，需将其逆变换回雷达参考系，可获得雷达系中准确的观测结果。空间场点r的散射场Es（r），Hs（r）是散射体所有微元贡献的叠加，可用积分形式表示：

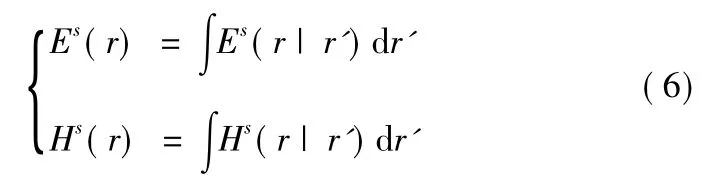
其中Es（r|r'），Hs（r|r'）表示散射体源点r'∈Ω在空间场点r的贡献，包含强度、频率和相位信息，积分范围为散射问题求解域，Ω表示散射体所在区域，理想导体或均匀介质散射体的求解域退化为散射体边界Ω。在雷达参考系中观测结果表示为

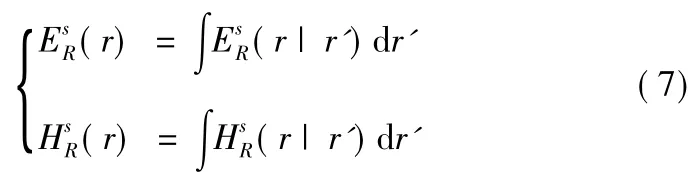
考虑雷达系与目标系的相互变换，则有

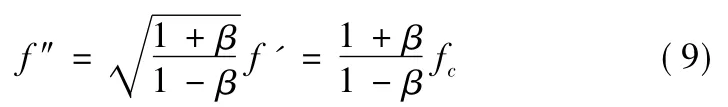
若目标为平动，各散射元贡献散射场频率相等；若目标存在转动模式，则雷达参考系观测到的散射场存在多个频率分量。

2 准静态原理

依据雷达参考系和目标参考系之间电磁场的相互转换关系，可以在理论上对任何动态目标的电磁散射问题进行精确求解。准静态原理在一定程度上简化了上述求解过程，本节将讨论这种简化的数学本质及其合理性和适用性。

对于动态目标与入射电磁场构成的非平衡态系统而言，系统变化的原因是目标的运动状态。在非常小的时间尺度T，运动目标的运动状态根据准静态假设处于近似恒定状态。因而，目标在运动状态相空间中的演变可以近似表征为一系列的准静态序列。因此，运动目标的电磁散射过程可以用一系列与运动状态的准静态相对应的电磁散射准静态近似。给定时刻的电磁散射动态系统，运动散射体对入射电磁场的散射作用等于该时刻准静态的运动状态对散射体的调制作用。动态目标的电磁散射强度等于当前姿态下静止目标的散射强度，动目标对于入射电磁场的频率调制等于当前目标速度的调制结果。即

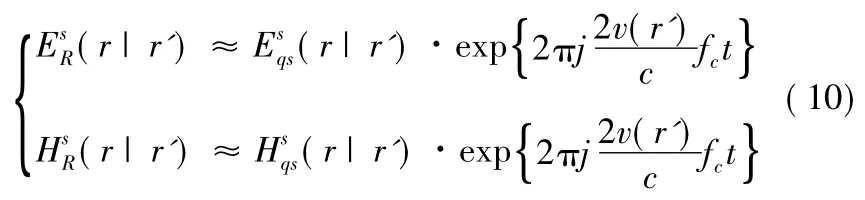
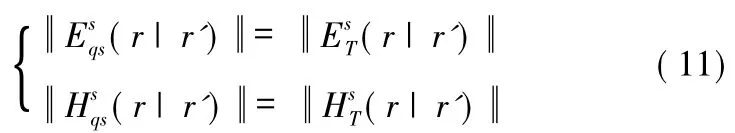
因此，基于准静态假设近似，即将运动散射元的散射强度和静止散射元的散射强度等同，等价于将如下两个电磁散射问题的解等同，问题A在雷达参考系中，入射电磁场边界条件为（Ei，Hi），准静态散射体的散射场，；问题B在目标参考系中，入射电磁场边界条件为（Ei（r'），Hi（r'）），散射体的散射场。A和B满足相同的电磁学规律，可用相同的数学形式刻画，其区别在于边界条件的形式差异。因此，准静态假设的实质是将电磁散射偏微分方程（或其等价积分方程）的边界条件入射电磁场，从（Ei（r'），Hi（r'））空间分布形式近似为（Ei，Hi）的均匀分布形式。入射场的偏差为（δEi（r'），δHi（r'）），其中δEi（r'）=Ei（r'）-Ei，δHi（r'）=Hi（r'）-Hi。散射场［Es（r），Hs（r）］，为入射场［Ei（r'），Hi（r'）］的泛函，表示在给定边界条件对电磁散射的偏微分方程的求解，电磁散射的精确解为EMScattering（Ei（r'），Hi（r'））类似地，准静态近似解为EMScattering（Ei，Hi），偏差［δEs（r），δHs（r）］= EMScattering［δEi（r'），δHi（r'）］。若（δEi（r'），δHi（r'））为小量，即为小量，则由此引发的散射场偏差也为小量［7］。对于雷达目标而言，其运动均处于非相对论层面，电磁散射入射场的精确形式与近似形式主要体现在微小的多普勒频移上，多普勒频移相对雷达信号的载频及其微小，因而可以认为入射场准静态近似是小量近似，从而可得散射场的近似解与精确解的偏差为小量，因而雷达目标的准静态近似合理的。

3 结束语

本文从电磁场在雷达参考系和目标参考系的相互转换关系出发，构建了适用于动态目标的精确电磁散射模型，模型立足于目标参考系中非均匀边界条件电磁散射问题的求解，化解了雷达参考系中的非稳态电磁系统的复杂表征，具有一定的普适性，适用于任何几何、材料和运动形式的空间目标。在对模型分析的基础上，讨论了基于准静态原理的动态目标电磁散射计算的合理性和适用范围。

［1］盛新庆.计算电磁学要论［M］.中国科学技术大学出版社，2008.

［2］Ishimaru A.Electromagnetic wave propagation，radiation，and scattering［M］.Prentice Hall Englewood Cliffs，NJ，1991.

［3］Feynman R P，Leighton R B，Sands M L，et al.费恩曼物理学讲义［M］.上海科学技术出版社，2005.

［4］向道朴.微多普勒回波模拟与微动特征提取技术研究［D］.长沙:国防科学技术大学，2010.

［5］赵凯华，罗蔚茵.新概念物理教程:电磁学［M］.北京:高等教育出版社，2008.

［6］钟珊珊.冲击线性信号的神经网络仿真［J］.重庆工商大学学报:自然科学版，2014，31（1）:69-73.

［7］Chen V.The micro-Doppler effect in radar［M］.Artech House，2011.

［8］Dieudonné J.History of Functional Analysis［M］.North-Holland，1983.

（责任编辑杨继森）

EM Scattering Model of Dynamic Rigid Target

ZHOU Cheng-hong，QIAN Wei-ping，GUO Yong-qiang
（Key Laboratory for Space Target Measurements，Beijing Institute of Tracking and Telecommunications Technology，Beijing 100094，China）

The EM scattering properties of static radar targets can be calculated accurately with mature computational EM methods，while dynamic targets are approximated under the quasi-static principle. Based on the transformation of Maxwell's equations and electromagnetic field boundary condition between radar reference frame and target reference frame，a mathematical of dynamic EM scattering problem，the so-called Maxwell's equations problems with non-uniform boundary condition，was put forward in target reference frame.Besides，the theoretical basis of quasi-static approximation was discussed，and we pointed out that it is appropriate for target with sub-relativistic velocity.

rigid motion；EM scattering；reference frame transformation；quasi-static principle

周城宏，钱卫平，郭永强.动态目标的电磁散射模型［J］.四川兵工学报，2015（11）：138-140.

format：ZHOU Cheng-hong，QIAN Wei-ping，GUO Yong-qiang.EM Scattering Model of Dynamic Rigid Target［J］. Journal of Sichuan Ordnance，2015（11）：138-140.

TM15

A

1006-0707（2015）11-0138-03

10.11809/scbgxb2015.11.037

2015-06-02

周城宏（1989—），男，助理研究员，主要从事认知雷达、雷达目标特性研究。