基于大视场光学跟踪测量系统的恒星定向研究

徐韬祜，孙华燕，张廷华，都琳

（装备学院a.研究生院；b.光电装备系，北京101416）

基于大视场光学跟踪测量系统的恒星定向研究

徐韬祜a，孙华燕b，张廷华b，都琳a

（装备学院a.研究生院；b.光电装备系，北京101416）

针对大视场光学跟踪测量系统提出了一种改进的快速定向的方法，通过拍摄星图，利用恒星确定的世界坐标与相面坐标解算光轴指向对应的方位角，从而实现定向的目的；首先推导了坐标系转换模型，然后分析了影响定向精度的误差因素，再次改进了星图识别算法；最后利用Matlab对提出的定向方法实现了软件化并进行了实验研究；实验结果表明：此方法可以用于大视场光学跟踪测量系统的野外定向。

光学测量；定向；大视场；星图识别

定向即寻北，为观测跟踪系统寻找零方位基准。目前常用的定向方法主要有几何定向法、磁定向法、天文定向法、陀螺经纬仪定向法、GPS定向［1］，天文定向以观测天体实现方位角测量，有行星定向［2］，太阳定向［3］，北极星定向，任意恒星定向［4］等方法，恒星定向是一种最常用和精度最高的天文定向方法。传统的光电经纬仪进行恒星定向时需要对准选定的恒星，然后进行方位解算，方位轴置零，无论是北极星定向还是其他恒星定向均针对单星。为使系统光轴准确指向选定恒星，文献［5］中还提出了恒星回扫法，使经纬仪沿不同方向指向选定恒星以减小方位轴晃动误差和随机测量误差。

对于大视场系统，视场内可以同时观测到数量较多的亮度高的恒星，因此可以利用视场内的多颗恒星解算主点对应的光轴指向的方位角。本文提出的基于姿态解算的定向方法，无需使光轴指向特定恒星，只需大致指向选定的恒星群，利用视场中的恒星解算出光轴指向的赤道坐标，根据测站坐标和曝光精确时刻得到光轴指向的方位角，然后对方位轴进行置数，同时此方法避免了跟踪系统在动态指向恒星过程中的轴系晃动影响。

1 基本原理

大视场系统恒星定向的基本原理如图1所示，系统拍摄星图并记录曝光时刻，通过星图识别得到若干亮星的赤道坐标，利用物空间像空间变换关系得到光轴赤道坐标，其中星图识别得到的是J2000时刻的赤道坐标，需要修正到当前纪元时刻的赤道坐标。最后通过时角法求取方位角，从而对方位轴置数实现定向。

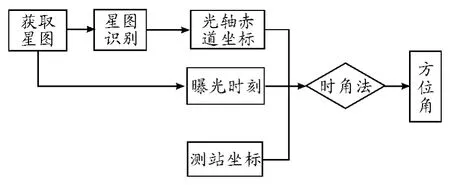
图1 基本原理

1.1 光轴赤道坐标求取

恒星成像于焦平面为点像，星点像素坐标与世界坐标的变换关系如式（1）表示，式中（u0，v0）表示主点坐标，（dx，dy）表示像元尺寸，（ui，vi）表示像面星点像素坐标。

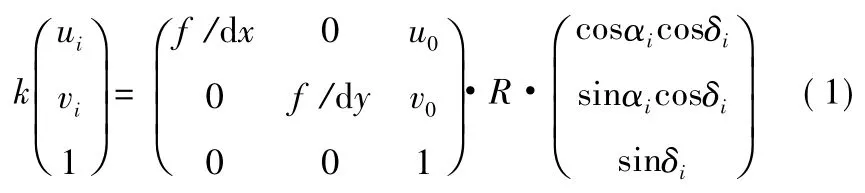
R表示旋转矩阵，如式（2）所示［6］：

（α0，δ0）即为光轴指向对应的赤道坐标，φ0表示相机坐标系相对于赤道坐标系的横滚角，转换关系中涉及到的内参数需要预先标定好，本文不予介绍。

1.2 赤道坐标地平坐标转换

赤道坐标地平坐标的转换采用时角法转换，各坐标系之间的关系如图2所示，其中（λ，φ）表示测站天文坐标，（h，A）表示光轴高度角方位角，（LHA，δ）表示恒星地方时角坐标，（α，δ）表示当前纪元光轴指向赤道坐标，GAST（Greenwich Apparent Sidereal Time）表示格林尼治真恒星时。

球面三角形PAS中内角K未知，由球面正弦定理可得一组方程：

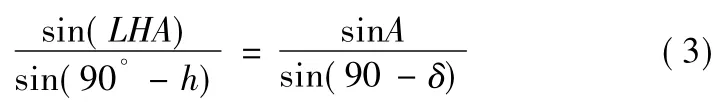
由球面余弦定理可得到方程：

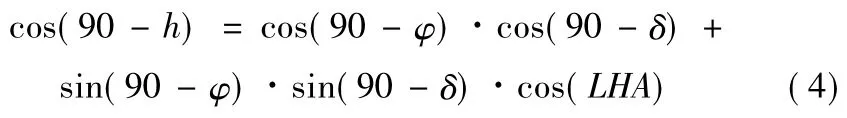
恒星地方时角、格林尼治真恒星时、赤道经度以及地理经度的关系为

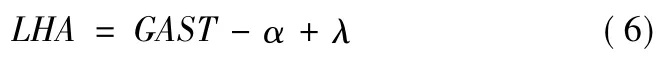
将式（3）代入式（5）可得：

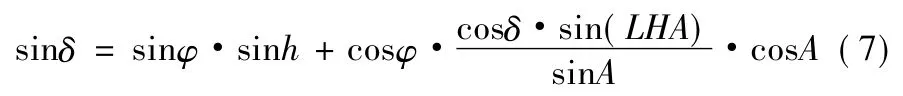
将式（4）代入式（5）得：

由式（8）得到：

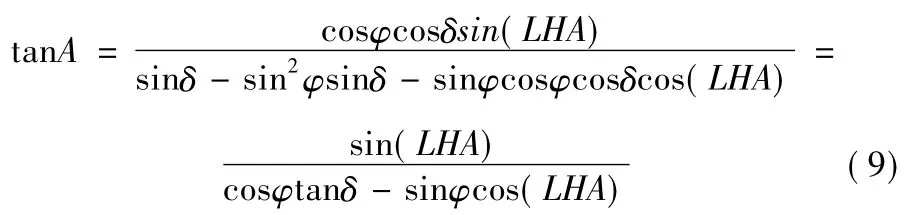
天文定向中，测站天文坐标（λ，φ）和恒星赤道坐标（α，δ）已知，由观测时间t可求得恒星地方时角LHA，利用上式就可求得方位角A。

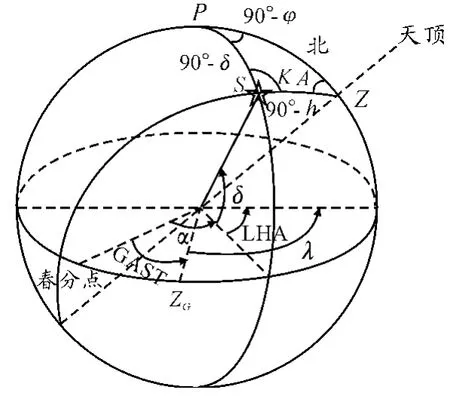
图2 坐标系转换关系

1.3 星图识别

星图识别技术是天文导航系统中的重要部分，特别是天基系统的星敏感器导航，星图识别要做到实时精确识别。本文提出的恒星定向方法中，星图识别是重要环节，并且无需实时处理，系统指向某一方位，拍摄星图后，无需实时处理获得方位信息，因此星图识别强调精确性。星图识别算法大多基于角距离和亮度信息。文献［7］改进三角形识别算法，将三角形信息投影为一维向量信息与模式星库比较，提高了识别效率；文献［8］提出了主星识别算法，一次识别四颗星，以一颗星作为主星，分别建立和其他三颗星的角距离与识别星库比较，再以剩余三颗星之间的角距离为识别模式去除识别冗余；文献［9］提出了带公共边的四边形星图识别算法，一次可以识别四颗星。由式（1）可得出，需要3颗星就可解算物像关系，样本数量越多解算结果越精确，考虑星图识别算法的精度及视场内的亮星数量，本文用5颗星解算物像变换关系。改进星图识别算法，采用三角形共角点法进行识别，一次识别五颗星，星图识别流程如图3所示。

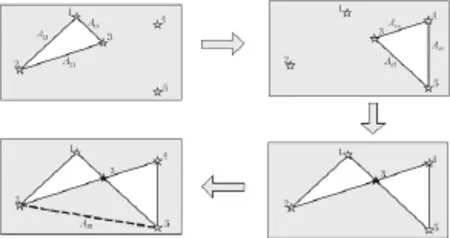
图3 星图识别流程

首先提取相面上最亮的五颗星，以星123，345分别组成三角形，利用角距离识别得到两组星，然后比较识别出的两组三角形中像面编号为3的公共星是否对应依巴谷星表中相同的星号，若无识别冗余则识别结束，若仍有识别冗余，则再添加一组角距离A25进行识别去除冗余。测试20张实拍星图，采用此方法均可识别。

2 定向误差分析

方位角计算式（9）表明方位角测量与测站位置φ，恒星地方时角LHA以及恒星的地心视位置δ，恒星地心视位置计算误差极小可忽略不计，恒星地方时角LHA又与测站经度λ和GAST有关。总体来说，忽略恒星地心视位置坐标转换误差，方位角测量误差主要与测站坐标（λ，φ）和观测时间误差有关。

方位角关于测站纬度求偏导

方位角关于恒星地方时角求偏导

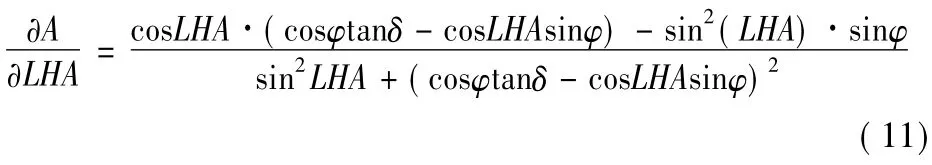
2.1 时间误差影响分析

方位角关于儒略世纪求偏导数：

则方位角关于儒略世纪的误差表示为

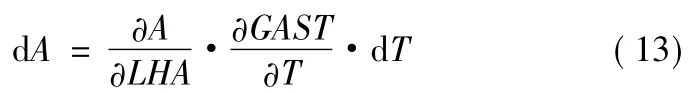
其中T为J2000时刻起算的儒略世纪数，格林尼治真恒星时由下式计算：

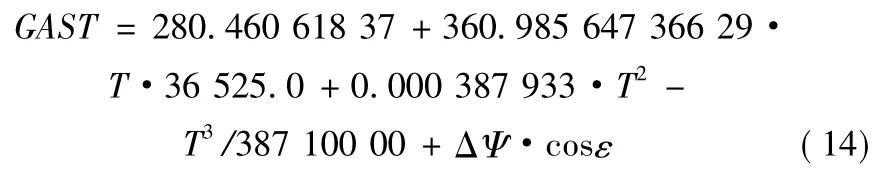
单位/（°），ΔΨ为黄经章动，ε为真黄赤交角，黄经章动和真黄赤交角均与儒略世纪数有关，黄经章动和真黄赤交角计算方法以及儒略世纪数关于北京时间的转换均可参见文献［10］。格林尼治真恒星时关于时间的偏导数也不再详细介绍，下面只给出方位角测量误差关于时间误差的误差曲线图，如图4所示，表示不同高度角，时间误差为1 000 ms时的不同方位角恒星定向误差曲线。

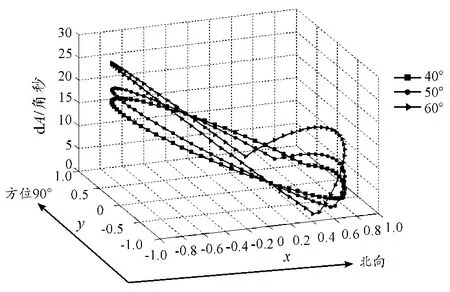
图4 时间误差曲线

由误差曲线可以看出方位角为0°（正北），高度角接近于40°时，即靠近北极星时，误差接近于零，且随着方位角的变化，误差缓慢上升。俯仰角继续增加时，各方向的误差均会上升。恒星定向时，误差曲线可以作为选星的参考。

2.2 测站定位误差影响分析

测站定位误差对定向的影响来自测站天文纬度误差和天文经度误差，测站天文纬度误差对方位角测量误差的影响可以表示为

由式（5）和式（9）可得：

将球面三角形的正弦和余弦方程带入上式，用高度角和方位角可将其表示为

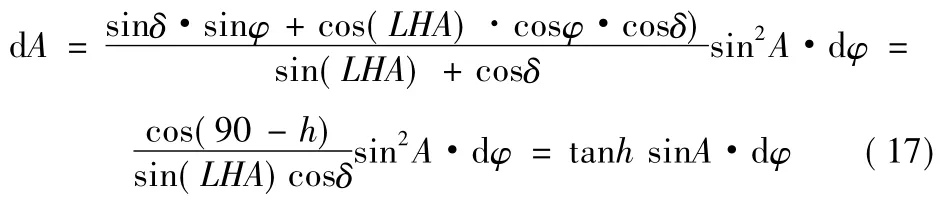
仿真了测站误差在20角秒时，测站误差在利用不同方位不同俯仰恒星定向时的定向误差，如图5所示。

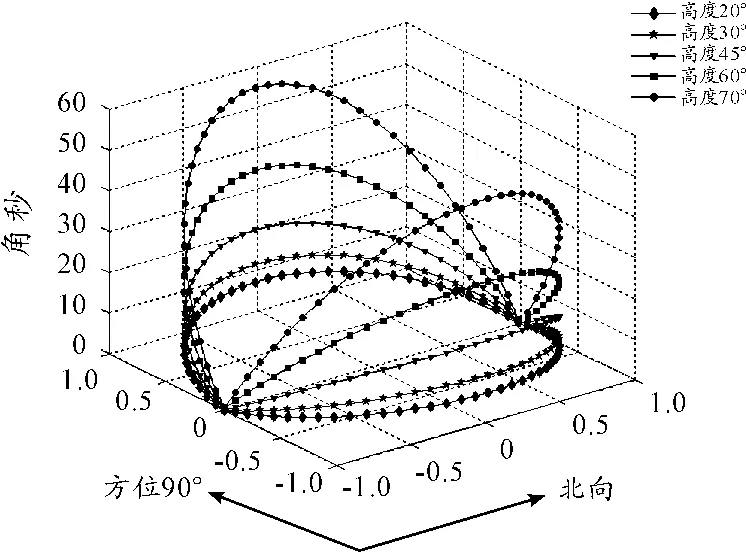
图5 定向误差关于测站纬度误差的曲线

根据误差曲线图，可以看出高度角越低，测站误差的影响越小，同时，方位角的选取也影响误差，正北和正南可以将测站纬度误差的影响降到最低。

方位角关于测站经度求偏导数

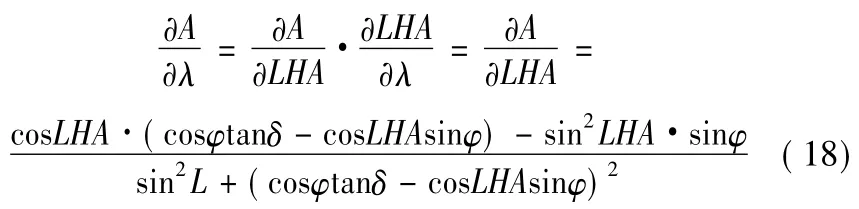
利用球面三角的正弦余弦方程，测站天文经度误差对方位角测量误差的影响可以表示为

不同方位角的误差关于测站经度的曲线与不同方位角的误差关于时间的曲线相似，因此选星按照时间造成的误差最小方案即可将测站经度误差造成的定向误差降到最低。

3 软件实现及实验研究

3.1 软件实现

利用Matlab将所述定向方法软件化，软件界面如图6所示。亮星星库筛选了依巴谷星表中亮于6.5星等的恒星作为星图识别的星库，亮星质心提取采用灰度加权的方法。

图6 恒星定向软件界面

3.2 实验研究

以某型号大视场试验设备进行实验研究，视场为5°× 3.5°，焦平面分辨率为3 456×5 184，其布站于北纬40.321 0°、东经116.620 2°。根据定向误差分析可知，选择北向的恒星群作为定向恒星群，可以显著降低由时间和测站位置误差导致的定向误差。因此选择北向附近的仙后星座恒星群作为定向恒星组，光轴指向静止不动，拍摄不同时刻的十二帧图像，分别求取光轴指向的方位角，实验数据如表1所示。

表1 仙后座光轴方位角解算结果°

根据实验结果319.872 258°对方位轴置数。

由于没有其他设备作为标准，因此方位轴置向后，转到容易识别的英仙座记录当前方位轴码盘输出值，以英仙座解算得到的结果和当前方位轴码盘输出的示数进行比较，作为此方法的定向精度分析。转台转到英仙座，此时方位轴输出指向为304°6'58”=304.11611°，同样拍摄不同时刻的十二帧图，解算光轴指向，实验数据如下（表2）。

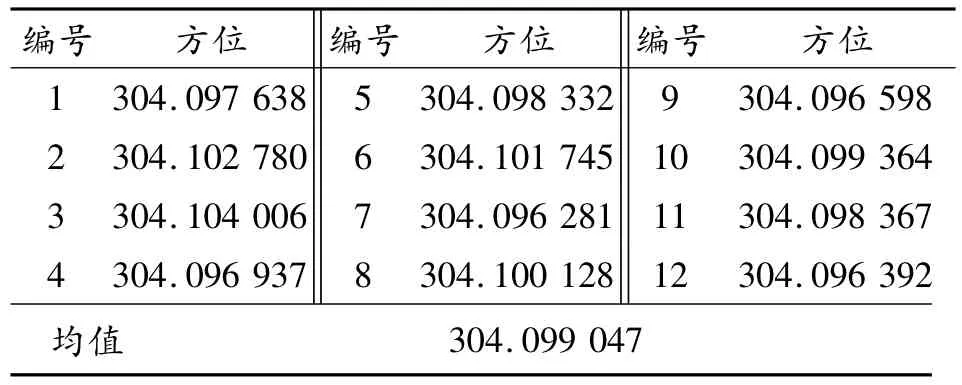
表2 英仙座光轴方位角解算结果°

由实验结果可知，此方法定向精度可达304.116 11°-304.099 047°=0.017 1°，相比横向视场角5°极小。

4 结论

本文利用物像空间变换模型，通过像面上恒星已知的世界坐标和像素坐标，解算光轴指向的赤道坐标，然后通过时角法求取方位角，为大视场系统的恒星定向提供了一种可参考的方法。实验结果表明此方法定向精度可达0.017 1°，对于大视场系统来说，得到了较好的定向效果。

［1］洪绍明，杨永平，段德磊.常用定向方法综述及其比较［J］.勘察科学技术，2008（1）:52-57.

［2］詹银虎，张超，华跃升，等.利用行星进行快速天文定向［J］.测绘科学技术学报，2012，28（5）:338-341.

［3］张超，郑勇，孟凡玉.利用测日实现快速天文定向［J］.测绘科学技术学报，2007，24（5）:343-345.

［4］张超，郑勇，李长会.用任意星进行天文定向的研究［J］.测绘科学，2005，30（4）:30-32.

［5］李增.车载经纬仪自主定位定向技术的研究［D］.北京:中国科学院，2010.

［6］彭华峰，陈鲸，张彬.天基光电望远镜空间多目标成像模拟技术研究［J］.光学技术，2007，33（2）:219-222.

［7］陆敬辉，王宏力，孙渊，等.基于P向量与三角形内切圆的星图识别算法［J］.光学技术，2011，37（1）:101-105.

［8］Roelof W H.van Bezooijen.True-sky demonstration of an autonomous star tracker［C］//SPIE's International Symposium on Optical Engineering and Photonics in Aerospace Sensing.International Society for Optics and Photonics，1994:156-168.

［9］孟靖.大地天文测量星图定位与识别算法的研究［D］.西安:西安电子科技大学，2010.

［10］Meeus J H.Astronomical algorithms［M］.Willmann-Bell，Incorporated，1998.

（责任编辑杨继森）

Research of Orientation by Stars Based on Wide Field Optical Tracking and Measuring System

XU Tao-hua，SUN Hua-yanb，ZHANG Ting-huab，DU Lina
（a.School of Postgraduate；b.Department of Optical and Electrical Equipment，Academy of Equipment，Beijing 101416，China）

We provided an orientation method aimed at wide field optical tracking and measuring system. By shooting star images and using stars'determined world coordinates and pixel coordinates to calculate the azimuth angle that optical axis pointing to，we realized the purpose of the orientation.At first，this paper deduced the coordinate transformation model.Then the paper analyzed the factors which affected the accuracy of orientation.Once again the star identification algorithm was improved.Finally，the method proposed was realized based on Matlab and the experimental research was implemented.Experimental results show that the method meets the demand of accuracy and can be used in field orientation of wide field optical tracking and measuring system.

optical measurement；orientation；wide field；star identification

徐韬祜，孙华燕，张廷华，等.基于大视场光学跟踪测量系统的恒星定向研究［J］.四川兵工学报，2015（11）：125-128.

format：XU Tao-hu，SUN Hua-yan，ZHANG Ting-hua，et al.Research of Orientation by Stars Based on Wide Field Optical Tracking and Measuring System［J］.Journal of Sichuan Ordnance，2015（11）：125-128.

P222

A

1006-0707（2015）11-0125-04

10.11809/scbgxb2015.11.033

2015-04-25

徐韬祜（1989—），男，硕士研究生，主要从事光电信息处理与对抗研究。