一类单种群扩散模型的正概周期解的定性分析

李晓艳，姚频，田丽娜

（兰州城市学院a.数学学院；b.附属中学，兰州730070）

一类单种群扩散模型的正概周期解的定性分析

李晓艳a，姚频b，田丽娜a

（兰州城市学院a.数学学院；b.附属中学，兰州730070）

讨论了一类具有时滞的单种群扩散模型，得到了正概周期解的存在条件，借助构造Liapunov函数，找到了正概周期解全局稳定的充分条件。

单种群；扩散；正概周期解

用数学模型的方法来研究种群生态学问题是常见的方法，它能够应用数学的技巧和方法来解释一些自然界所存在的现象。对于整个生态系统而言，只研究其中的单一种群是应该首先考虑的。在现实生活中，有些单种群物种会在若干个不同环境之间移动，这样就造成了种群间的扩散，由于具有斑块扩散的单种群模型的周期解问题的结论较多，而概周期现象是一类比周期现象更普遍的现象，因此研究概周期问题的重要性不言而喻［1-3］。

讨论模型

其中x1，x2分别表示种群X在斑块1和斑块2的种群密度，以下均假设ai（t），bi（t），Ci（t），Di（t）（i=1，2）均是连续非负的函数且ai（t），bi（t）严格正，并且τi（t）≥0，i=1，2，3。

1 系统的持久性

定理2若系统方程式（1）满足以下假设（A1）bi（t）＞Ci（t），t∈R，i=1，2，则系统方程式（1）的解在中最终有界。

由bi（t）＞Ci（t），观察等式右边，前后两项均为二次项系数为负的二次代数式，故易知存在L1，L2，使得f（x1）= x1［η+a1（t）-b1（t）x1（t）+C1（t）x1（t-τ1（t））］≤L1，f（x2）=x2［η+a2（t）-b2（t）x2（t）+C2（t）x2（t-τ2（t））］≤L2，即。

定理3若假设（A2）；成立，则系统方程式（1）是可持续的。

故系统方程式（1）是可持续的，并且Ω=｛（x1，x2）|xi≥ mi＞0，，x1+x2＜M｝是方程式（1）的一致最终有界区域。

2 概周期解存在性和全局稳定性

以下均假设系统方程式（1）中ai（t），bi（t），Ci（t），Di（t）（i=1，2），τi（t），i=1，2，3.均是连续非负的概周期函数，且ai（t），bi（t）严格正。下面考虑方程式（1）的概周期解存在性和全局稳定性。

考虑方程式（1）的伴随系统

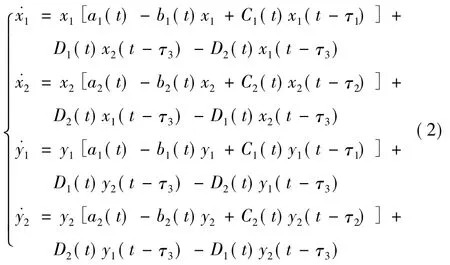
引理1［1］设D是的一个开集，函数V（t，x，y）定义在R+×D×D上满足

1）a‖x-y‖≤V（t，x，y）≤b‖x-y‖，其中a（r）和b（r）为连续、递增的正定函数；

2）‖V（t，x1，y1）-V（t，x2，y2）‖≤k｛‖x1-x2‖+‖y1-y2‖｝，k＞0是一个常数；

4）若满足t≥t0＞0的解位于紧集S中，S⊂D；

则系统方程式（2）在D中有唯一概周期解P（t）；若P（t）位于紧集S中，则该概周期解是一致渐近稳定的。

假设（A3）

定理1若概周期系统方程式（2）满足假设（A2）和（A3），则系统存在唯一的正概周期解，且此解是全局渐近稳定的［4-8］。

证明：由定理2知紧集Ω是系统方程式（1）的最终有界区域。定义Xi（t）=lnxi（t），Yi（t）=lnyi（t）；X（t）=（X1（t），X2（t）），Y（t）=（Y1（t），Y2（t）），x（t），y（t）是伴随系统方程式（2）在Ω×Ω上的解。

［1］Song X Y，Li Y F.Dynamic behaviors of the periodic predator-prey model with modified Leslie-Gower Holling-type II schemes and impulsive effect［J］.Nonlinear Analysis:Real World Applications，2008（10）:64-79.

［2］陈超，纪昆.具有Holling III类功能性反应的多种群竞争捕食系统的概周期解［J］.应用数学学报，2006，29（4）: 756-765.［3］薛炜.污染环境中Gompertz食饵—捕食者系统的全局吸引性［J］.甘肃科学学报，2013，25（3）:12-15.

［4］Liu X N，Chen L S.Complex dynamics of Holling type II Lokta-Volterra predator-prey system with impulsive perturbations on the predator［J］.Chaos Solitons Fractals，2003（16）:311-320.

［5］Hale J.Theory of Functional Differential Equations［M］. Heidelberg:Spinger Verage，1977.

［6］陆征一，周义仓.数学生物学进展［M］.北京:科学出版社，2006.

［7］马知恩.种群生态学的数学建模与研究［M］.合肥:安徽教育出版社，2000.

［8］马知恩，周义仓.常微分方程定性与稳定性方法［M］.北京:科学出版社，2001.

（责任编辑杨继森）

A Qualitative Analysis of Diffusive Single-Species of Positive Almost Periodic Solution

LI Xiao-yana，YAO Pinb，TIAN Li-naa
（a.Institute of Mathematics；b.Attached Middle School，Lanzhou City University，Lanzhou 730070，China）

A diffusive single-species with time delays was investigated.The positive almost periodic solution was found.By means of constructing Liapunov function，the sufficient condition which guarantees the global asymptotic stability was obtained.

single-species；diffusion；positive almost periodic solution

李晓艳，姚频，田丽娜.一类单种群扩散模型的正概周期解的定性分析［J］.四川兵工学报，2015（11）：136-137.

format：LI Xiao-yan，YAO Pin，TIAN Li-na.A Qualitative Analysis of Diffusive Single-Species of Positive Almost Periodic Solution［J］.Journal of Sichuan Ordnance，2015（11）：136-137.

O175.13

A

1006-0707（2015）11-0136-03

10.11809/scbgxb2015.11.036

2015-06-22

国家自然科学基金（11261027）；2014陇原青年创新人才扶持计划项目

李晓艳（1980—），女，硕士，讲师，主要从事生物数学研究。