多级联调机构的六西格玛设计及响应面法优化

赵 雷，采 峰，马 召

（1.中航工业沈阳发动机设计研究所，沈阳110015；2.中航工业发展研究中心，北京100029）

0 引言

燃气轮机上多级联调机构用于连接多级静子，并同时驱动多级联动环，使各级静子叶片的角度在风扇或压气机一定转速范围内按照一定规律变化。其设计难点在于各级静子叶片角度随转速的匹配关系。传统的连杆机构设计有解析法、作图法、实验法，但是普遍存在工作繁琐、效率低下、误差较大的问题，设计输入即规律变化时需全盘推倒重做。解析法虽然精确度较高，但构建位置方程相当复杂，计算求解也比较麻烦，难以推及一般可调机构工程设计应用[1-2]。

六西格玛设计(DFSS)是以数理统计为基础，从获得数据、处理数据和分析数据方面综合运用多种定性或定量的统计工具得出结果或趋势推论的综合性设计理念。完整的DFSS流程包括定义、测量、分析、设计、验证几个阶段。DFSS运用CDM和RDM工具分析客户需求，用SIPOC工具统计输入和输出变量并进行重要度分析，运用多层QFD质量工具识别关键节点和客户需求的耦合关系，并进行FMEA失效模式及风险分析，为后续全因子试验设计DOE提供基础。通过回归方程和假设检验可以建立定量的转换函数供最后的优化设计使用[3-4]。

本文探讨了1种基于六西格玛数据分析的操纵机构设计方法，通过对机构输入和输出数据的试验设计（DOE）和采集，运用科学严谨的数理统计工具，对影响输出的有效输入参数项进行了定量筛选和统计检验，建立了输入和输出参数间的响应模型，并对输出参数做了望目优化，分析过程和结果均有统计数据支持，具有求解快速、便于误差分析、对调节规律的更改反应快速的特点。

DFSS设计流程最后还包含验证阶段、制定测试计划、开展验证研究，以确定最终的设计结果，为突出重点，本文忽略了验证阶段研究的描述[5]。

1 联调机构的问题域分析

联调机构作为4连杆多体运动机构，实质是函数再现求解问题。多体运动机构一方面是已知各连杆参数，求解输出端的运动规律，另一方面是反问题，即已知运动输出端运动规律，求解满足条件的各连杆参数。2个问题皆可用1个方程来表示

式中：Y 是输出；x 是连杆参数。

无论是已知x 求y 的方程求解，还是已知y 求x的优化问题，都需要首先建立这个函数关系式。

联调机构的连杆参数和输出端规律响应，可以认为是多元线性回归模型

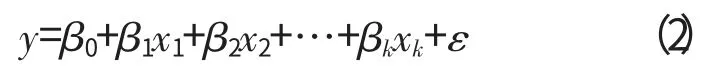
式中：βk为未知回归系数。

联调机构的求解即归结为对回归系数的求值，其数学上的工作为：求解回归方程；对式（2）的假设检验，确定模型的有效性；方差分析(ANOVA)，表明至少有1个变量对响应的贡献是显著的。

确立了回归方程且通过了假设检验，可以运用此方程对联调机构正反问题进行求解。

2 全因子2水平试验设计选择因子

DOE可用于系统地调查影响产品质量的过程变量或产品变量。确定影响产品质量的过程条件和产品组件后，可以有针对性地进行改进，以增强产品的可制造性、可靠性、质量和现场性能。

由于资源有限，从执行的每个试验中获取最多信息是非常重要的。与未经计划的试验相比，设计完善的试验可以产生更多信息，而且通常需要较少的游程。此外，设计完善的试验还将确保可以评估已确定为重要因素的效应。例如，如果相信2个输入变量之间存在交互作用，则确保在设计中包括这2个变量，而不是进行“1 次1个因子”试验。当1个输入变量的效应受另1个输入变量的水平影响时，就会出现交互作用。

本项目中，通过QFD等质量工具初步挑选了4个机构参数用于试验设计的因子分析[8-9]，分别为调节臂长度、角度、拉杆座半径、角度。该方法便于先期过滤因子，减少数据收集量和DOE分析计算的步骤。进行DOE的目的，是分析这4个参数各自及交互高次项对响应的影响。采用4因子2水平的全因子试验设计，包含中心点以考察弯曲效应。这样将共有24+1=17次试验项。

响应值的数据收集可通过加工试验件实物装配打压获得，但需加工16套不同规格的连杆和调节臂，加工和装配工作量巨大、成本很高。本项目采用UG运动学模块建立机构运动仿真模型，分析机构内各零件的运动副关系，设置运动初始态和边界条件，记录运动全过程位置数据，求得每个试验项的响应值并填入正交表中供后续分析使用[6-9]。

3 分析因子设计

采用Minitab软件进行分析，分析结果及残差如图1所示，效应分析见表1。从表中可见，P值是否小于0.05可判定该因子效应是否显著，即对响应影响较大，是必须要考察的因子。由图1可分析此次分析的可信度。

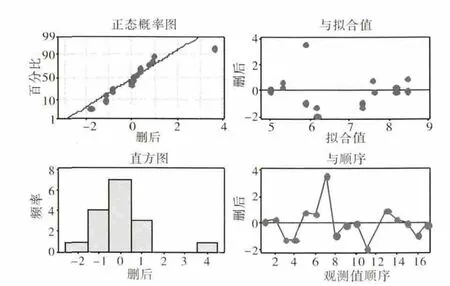
图1 残差

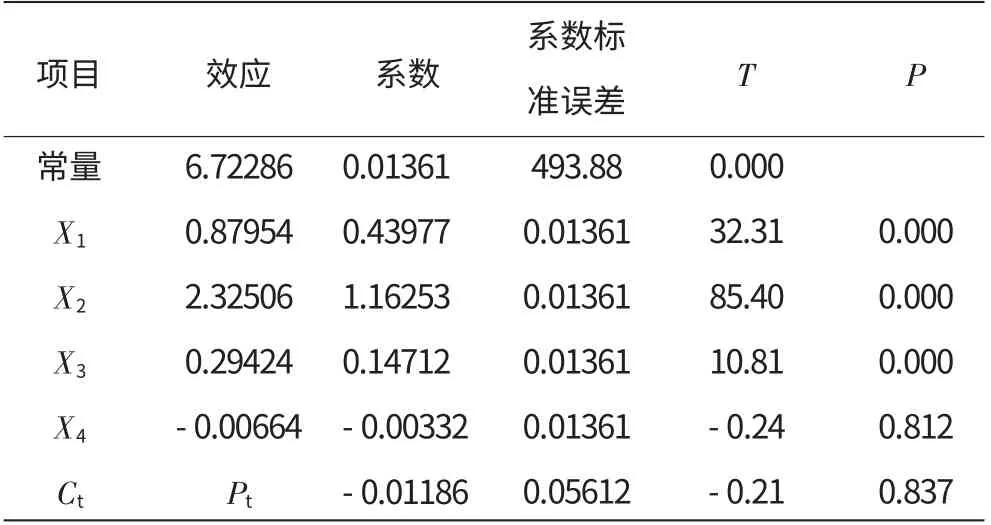
表1 DOE效应分析

从图中可见，残差分布符合正态分布，随机无规律，残差和为零。

响应方差分析见表2。

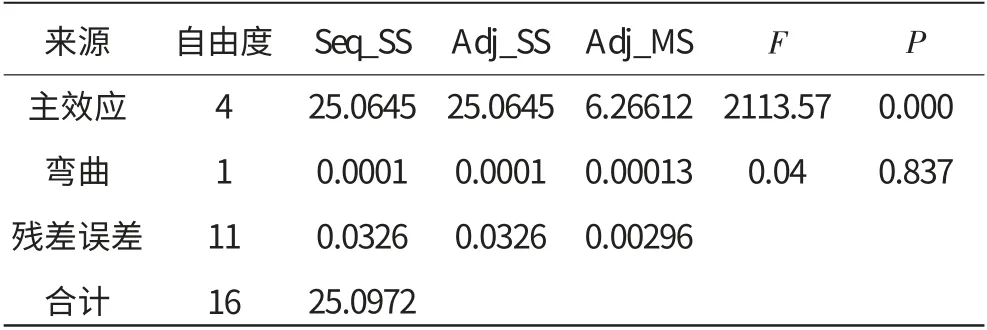
表2 DOE方差分析

从表中得出如下结论：

（1）主效应P值小于0.05，说明至少有1个因子显著；

（2）常量、X1、X2、X3的P值小于0.05，是显著项；

（3）弯曲P值过大，说明弯曲效应不显著。

由此说明此次分析各因子阶次及交互作用合理可用，效应显著，即式（2）成立。

4 响应面模型分析及优化

响应曲面法（RMS-ResponseSurfaceMethodology）是结合了数学方法和统计方法，以试验设计为基础的用于多变量问题建模和分析的1种统计处理技术。

当确认了少数重要因子后，采用响应曲面模型来建立响应方程，并寻找可以产生最佳响应的因子设置。可按如下步骤进行：

（1）给出因子2水平值，生成正交表；

（2）求得每项运行的响应值，完成正交表；

（3）按因子2次项、交互项、1次项进行响应面分析；

（4）根据分析结果和残差图进行判定，分析结果见表3。

响应方差分析见表4。

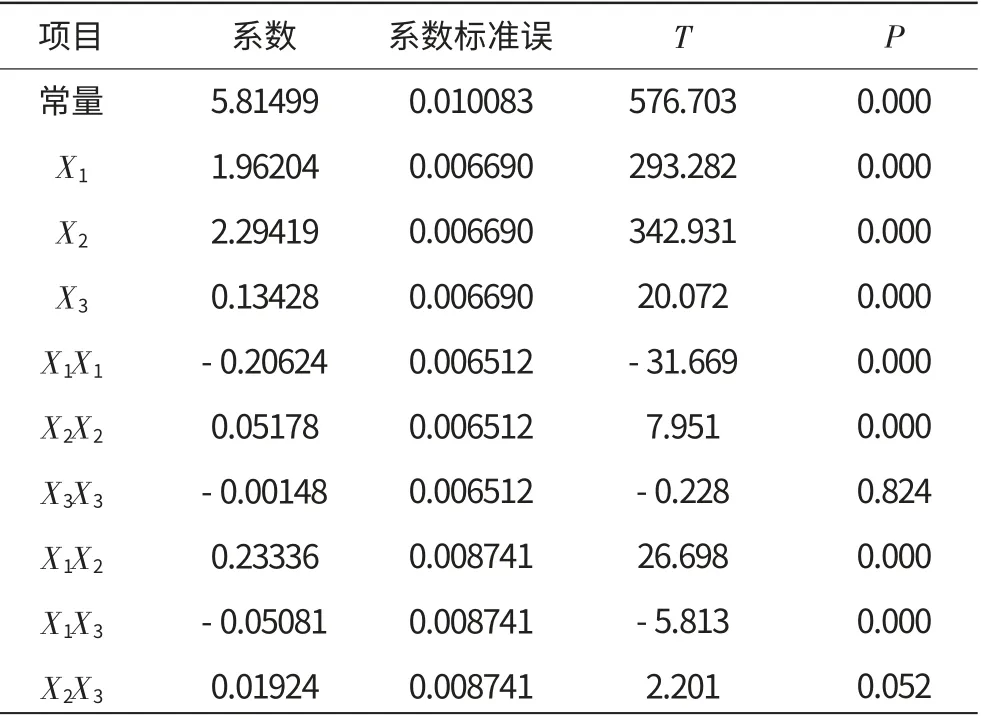
表3 RSM效应分析

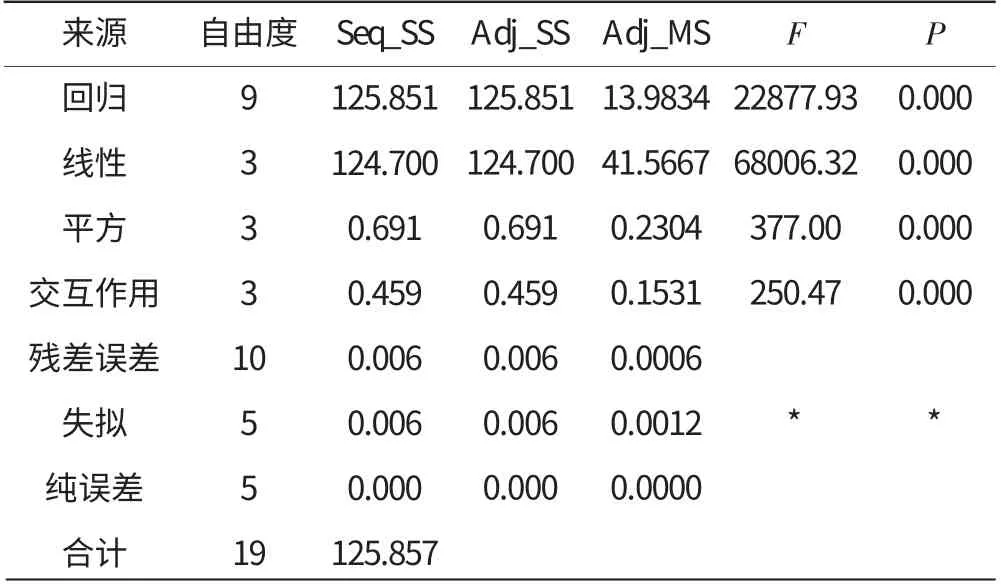
表4 方差分析

由表3、4中的方差分析结果可得：

（1）回归有效，线性和2次项、交互作用同样显著；

（2）常量、X1、X2、X3和除X3的2次项外所有2次项均显著。

响应面模型如图2所示。图中是保持X3的水平，及X1、X2因子对响应的综合效应，在因子取值区间内对响应Y 的分布形成1个曲面。从图中可见使Y 取值最小的X1、X2的范围。这也是后文优化的基础[10-12]。

分析所得去量纲化系数即为式（2）中的回归系数，从而建立此响应面数学模型。

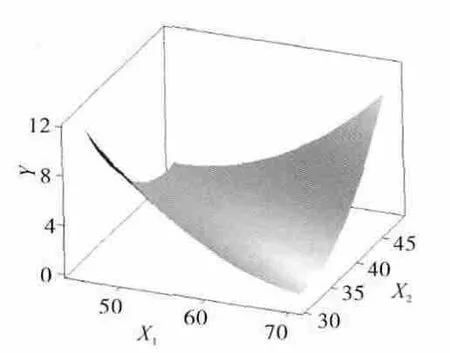
图2 响应面模型

5 蒙特卡罗法公差分配设计

以上对联调机构的设计，通过对试验数据的分析，识别了关键因子，建立了数学模型，并用优化的方法确定了各因子的取值。为进一步降低机构的制造成本，提高质量，有必要根据响应公差对各因子的制造容差进行分配，在此采用蒙特卡罗法进行公差分析，模拟各因子在不同公差容限配对条件下的响应，避免等公差设计或经验设计的不足。

蒙特卡罗法是1种模拟抽样仿真算法，可以对任意分布进行模拟。机械零件的制造误差随机分布，可认为符合正态分布，机械零件的公差可用±3σ 表示。为满足一定的计算精度，模拟可增加计算次数[13-15]。蒙特卡罗模拟结果如图3所示。

从图中可见，各因子的公差对响应的敏感度不同，在设计中可以对敏感度较高的因子给予较严格的公差，对敏感度低的因子给予相对宽松的公差，这样在制造上节约了成本。

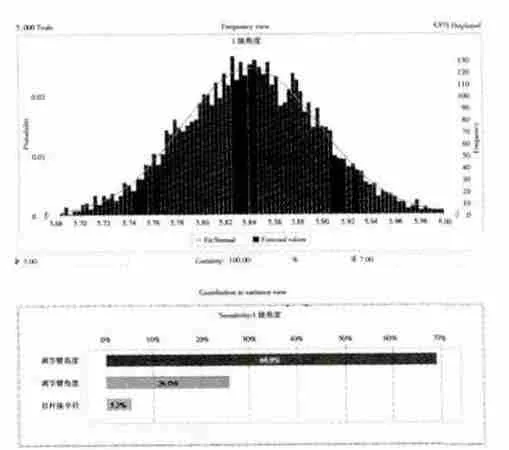
图3 蒙特卡罗模拟结果

6 结束语

通过六西格玛设计理念，将数理统计理论与相关工具结合起来，规范了设计过程，为设计决策提供坚实的数据支持。项目实践证明，六西格玛设计方法科学、有效，不仅可满足设计任务，还可以完成设计方法的梳理，可用于设计模型的建立，在工程实践中具有一定实用价值。

[1]孙恒，陈作模，葛文杰.机械原理（7版）[M].北京：高等教育出版社，2006：109-139．SUN Heng，CHEN Zuomo，GE Wenjie.Theory of machines and mechanisms(seventh edition)[M].Beijing：Higher Education Press，2006：109-139.（in Chinese）

[2]杨勇刚，张力.几种摇臂与联动环连接结构对比分析[J].航空发动机，2012，38（6）：34-37．YANG Yonggang，ZHANG Li.Contrast analysis of several rocker and drive ring connecting structure[J].Aeroengine，2012，38（6）：34-37.（in Chinese）

[3]邹峰，汪邦军，郝建春.航空工业六西格玛设计流程模式研究[J].航空标准化与质量，2009（1）：25-27.ZOU Feng，WANG Bangjun，HAO Jianchun.Aeronautic industry Six Sigma Design pattern research[J].Aeronautic Standardization and Quality，2009（1）：25-27.（in Chinese）

[4]何桢，梁昭磊，邹峰.六西格玛设计模式及其应用[J].工程机械，2006（7）：62-64.HE Zhen，LIANG Zhaolei，ZHOU Feng.Six Sigma Design pattern and application construction machinery and equipment[J].Engineering Machinery，2006（7）：62-64.（in Chinese）

[5]段爱琴，王兴华.应用六西格玛设计究竟改变了什么?[N].中国航空报，2011-04-12（12）.DUAN Aiqin，WANG Xinghua.What did DFSS changed us？[N].China Aviation News，2011-04-12（12）.(in Chinese)

[6]胡小康.UG NX4运动分析培训教程[M].北京：清华大学出版社，2006：136-147．HU Xiaokang.UG NX4 kinematics simulation training guide[M].Beijing：Tsinghua University Press，2006：136-147.（in Chinese）

[7]郭晓宁.连杆机构的结构运动学特征及参数化实体运动仿真的研究[D].西安：西安理工大学，2003.GUO Xiaoning.Research on structural and kinematic characteristics and parameterized solid kinematic simulation of linkages[D].Xi’an：Xi’an University of Technology，2003.（in Chinese）

[8]卫江红.基于SolidWorks的连杆机构的运动分析与仿真[D].大连：大连理工大学，2006.WEI Jianghong.Kinematic analysis and simulation of the linkages mechanism based on SolidWorks[D].Dalian：Dalian University of Technology，2006.（in Chinese）

[9]焦丽丽，张达明.UG在机构运动分析应用中关键技术的研究[J].机械设计与制造，2009（5）：94-96．JIAO Lili，ZHANG Daming.Research on key technologies of using UG software in the application of motion analysis[J].Machinery Design and Manufacture，2009（5）：94-96.（in Chinese）

[10]刘鸿恩，张列平.质量功能展开(QFD)理论与方法研究进展综述[J].系统工程，2002，18（2）：1-6.LIU Hongen，ZHANG Lieping.Review on QFD theory and method research progress[J].Systems Engineering，2002，18（2）：1-6.（in Chinese）

[11]孙玲玲.基于QFD和DOE的产品优化设计研究[D].杭州：浙江大学，2011.SUN Lingling.Research of product optimization design based on QFD and DOE[D].Hangzhou：Zhejiang University，2011.(in Chinese)

[12]罗世彬，罗文彩，王振国.基于试验设计和响应面近似的高超声速巡航飞行器多学科设计优化[J].导弹与航天运载技术，2003（6）：2-9.LUO ShiBin，LUO Wencai，WANG Zhenguo.Design of experiment and response surface approximation methods in multidisciplinary design optimization for hypersonic cruise vehicle[J].Missles and Space Vehicles，2003（6）：2-9.(in Chinese)

[13]赵妙霞，蒋钧钧.机械精度设计中机械制造系统误差的特征分布[J].甘肃工业大学学报，2001（4）：37-39.ZHAO Miaoxia，JIANG Junjun.Characteristic error distribution of machine-building system for high precision design[J].Journal of Gansu University of Technology，2001（4）：37-39.(in Chinese)

[14]袁贵星，王平.蒙特卡洛模拟及其在公差设计中的应用[J].天津科技大学学报，2008（2）：60-64.YUAN Guixing，WANG Ping.Monte Carlo simulation and its application in tolerance design[J].Journal of Tianjin University of Science and Technology，2008（2）：60-64.(in Chinese)

[15]庞晓红.基于Excel的蒙特卡洛法及其在工程设计上的应用[J].漳州职业技术学院学报，2006（3）：20-23.PANG Xiaohong.Monte Carlo simulation based on EXCEL and its application in design[J].Journal of Zhangzhou Technical Institute，2006（3）：20-23.(in Chinese)