不确定运行环境下航空发动机部件寿命计算

陈小磊，郭迎清，闫星辉，姜彩虹

（1.西北工业大学动力与能源学院，西安710072；2.中航工业无锡航空动力控制系统研究所，江苏无锡214100；3.中航工业沈阳发动机设计研究所，沈阳110015）

0 引言

随着新一代航空发动机对经济性要求的提高，寿命延长控制逐渐成为航空发动机控制领域的研究热点。其研究关键技术之一是准确计算部件寿命，旨在保证发动机性能不变或有少量损失的同时，大幅度延长发动机及其部件寿命[1-2]。航空发动机部件寿命计算非常复杂，其难点在于如何权衡发动机安全运行和部件使用最大化，保证发动机安全性的同时降低使用成本[3-4]。在发动机制造过程中，利用先进的工具分析所有部件的失效模式；再利用标准运行任务循环确定部件最大损伤，并根据该值计算部件的安全寿命[5]。航空发动机设计定型后，根据剩余起降或加减速循环次数来确定部件的剩余寿命，通常不再考虑发动机实际运行环境[6-8]。使用最大损伤来计算部件安全寿命在一定程度上保证了发动机运行的安全性，但有很大局限性，即大量部件未完全破损就提前维修或更换，而部分部件在安全寿命结束前就已经完全破损，增加了发动机运行的危险性[9-10]。发动机部件的寿命取决于其自身实际负载，如温度、压力等，这些因素与发动机实际运行过程密切相关，外部运行环境变化、发动机内部噪声、传感器或执行机构等不确定性因素也会影响发动机实际运行，进而影响部件实际使用环境，均可导致部件寿命发生变化。

由于传统寿命计算方法难以考虑上述不确定性因素，很难分析这些因素对寿命计算的影响。发动机传感器测量信息中包含了运行环境及发动机内部各种不确定性信息，因此可以采用基于传感器数据的寿命计算模型来计算航空发动机不确定运行环境下叶片的寿命。

本文以某型军用涡扇发动机高压涡轮导向叶片热机械损伤寿命为例，研究不确定运行环境下叶片寿命计算方法。

1 叶片TMF寿命模型及仿真系统

通常利用标准起降或加减速循环次数来计算部件的使用寿命，文献[11]已建立某型军用涡扇发动机寿命关键部件——高压涡轮导向叶片在单次加减速循环过程中的TMF(ThermalMechanicalFatigue)寿命模型，简单表示为

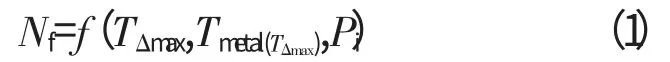
式中：Nf为叶片安全寿命；TΔmax为叶片前、后缘最大温度差；Tmetal(TΔmax)为叶片前、后缘最大温度差下叶片金属温度；Pi为发动机运行时部分截面压力。

上述参数均可表示为发动机运行过程中温度、压力的函数，而温度和压力由传感器测得或由机载模型提供。在无噪声环境下，不考虑其他诸如外部运行环境、加速终值、发动机退化等因素的变化，叶片每次标称加减速循环所经历的损伤相同。但在实际运行过程中，受发动机内部噪声、执行机构和传感器测量噪声以及运行环境变化的影响，叶片周围的温度和压力值会发生变化，从而导致叶片每次循环所受的损伤不同。因此，在非标称运行环境中，将某一固定Nf作为部件的寿命是无效的，甚至会增加发动机运行的危险性。

考虑到外部运行环境、噪声等各种因素均会对Nf产生影响，因此将Nf看作随机变量，利用概率统计理论来确定Nf。这里定义Nfn为叶片在标称运行环境下的安全寿命，Nfa为非标称运行环境下的安全寿命。那么标称运行环境下使用n次循环后，叶片失效概率为

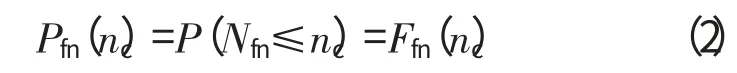
式中：Ffn为Nfn的累积分布函数；Pfn为叶片在非标称运行环境下的失效概率。

研究目的是寻找Pfn（nc）和Pfa（nc）之间的关系，以确定在非标称运行环境下，叶片失效概率及等效使用寿命。

文中构建的仿真系统结构如图1所示。

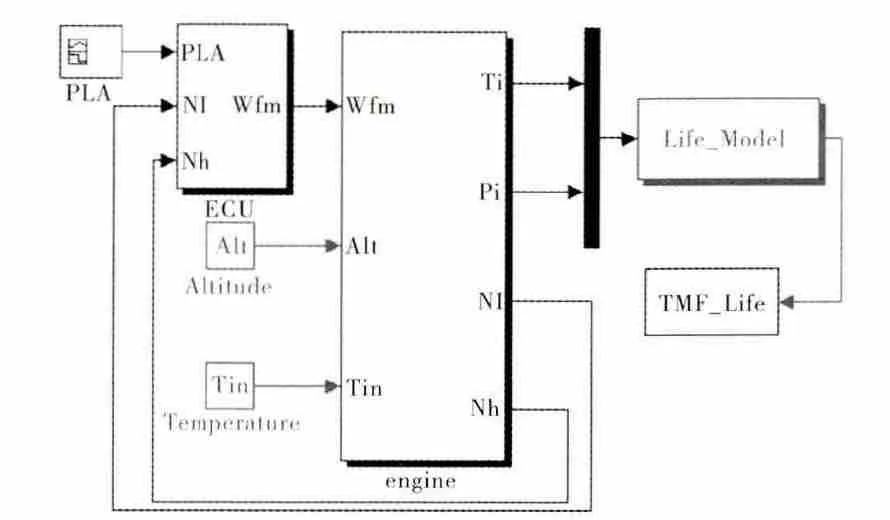
图1 仿真系统结构

图中，engine为某型军用涡扇发动机模型；ECU为其对应的变增益PID控制器；LifeModel为叶片寿命计算模块。仿真系统输入包括外部环境（高度和大气温度）、油门杆角度；输出为叶片在加速循环过程中的总应变差及在此应变差下叶片TMF可使用寿命。

2 叶片失效概率及等效使用寿命估算

因噪声呈随机分布特征，叶片寿命难以使用某一确定值来衡量，本文使用概率统计的方法来描述叶片使用寿命情况。工业中常用的产品寿命分布类型有：指数分布、正态分布、对数正态分布和威布尔分布等[12]。其中威布尔分布因其通用性强得到广泛应用，指数分布、正态分布及瑞利分布等可看作是威布尔分布的特例。航空发动机部件寿命分布也主要使用威布尔分布[13-14]。

2.1 威布尔分布

威布尔分布是随机变量分布之一，又称韦伯分布、韦氏分布，由瑞典物理学家WallodiWeibull于1939年引进，是可靠性分析及寿命检验的理论基础。威布尔分布在可靠性工程中被广泛应用，尤其适用于机电类产品的磨损累计失效的分布。因易利用概率纸推断出其分布参数，被广泛应用于各种寿命试验的数据处理。

目前，2参数的威布尔分布主要用于滚动轴承的寿命试验以及高应力水平下的材料疲劳试验，3参数的威布尔分布用于低应力水平的材料及某些零件的寿命试验，具有比对数正态分布更大的适用性。其概率密度函数为

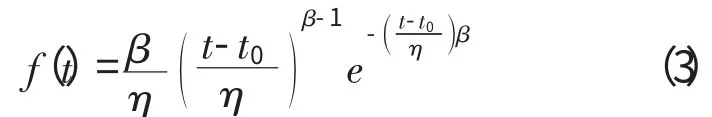
故障累积概率为

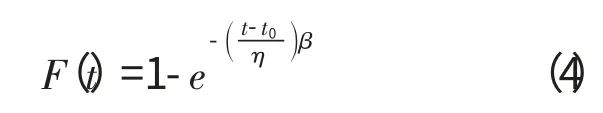
式中：β 为形状参数，影响威布尔分布曲线的形状，在“威布尔概率纸”上称为威布尔斜率；η 为尺度参数，影响分布的离散程度；t0为位置参数，影响分布曲线起点的位置。

这3个参数通常由试验确定。若t0=0，则为2参数的威布尔分布。

2.2 威布尔参数的估计

当前影响威布尔分布在寿命分布领域广泛应用的主要因素是如何精确估计上述3个参数。资料显示，威布尔分布参数通常由试验确定，即通过一定次数的试验，记录产品失效的时间或者循环次数，然后利用威布尔图来确定参数值。

令式（4)中t0=0，则式中只剩下2个参数β 和η，通过移相、取对数，最终得到

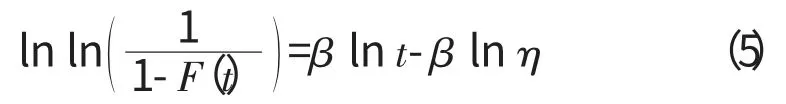
可简写成

这是1条不通过零点，斜率为β 的直线。通常采用双对数坐标纸（如图2所示）来确定威布尔参数。图中纵坐标表示失效发生累积率，横坐标表示失效发生的数量，这里为叶片的使用寿命。将试验数据在图中标出，并拟合成1条直线，则直线的斜率就是威布尔分布的参数β，而另一参数η 为直线上纵坐标为0.632所对应的横坐标值。

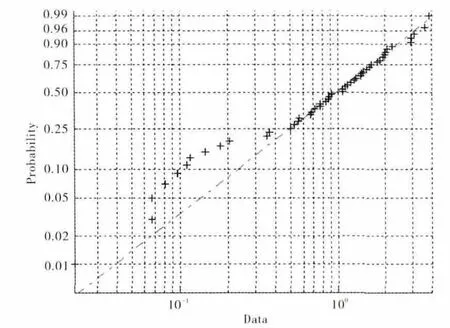
图2 威布尔图

由于未进行实物试验，因此设定η 为标称运行环境下发动机标称加速循环计算得到的叶片可使用寿命，也即η=34900，而β=4，根据“10%法则”[15]，设定安全寿命为3490次标称循环时，叶片失效概率为0.01%。在工程应用过程中，这些参数可以使用上文方法进行估计。

在标称运行环境下发动机运行 次加减速循环后，叶片失效概率可表示为

2.3 非标称运行环境下叶片失效概率计算方法

为了分析非标称运行环境下叶片的失效概率，需要统计出在额定运行循环nc下叶片失效次数。为了与标称运行环境进行对比，这里选取nc=3490。计算Pfa（3490）的前提是必须知道Nfa的分布情况。发动机运行环境与叶片寿命没有直接联系，很难确定其分布情况。为了避免该问题，可以利用MonteCarlo仿真来解决非标称运行环境下叶片失效概率计算问题[16-17]。

在Matlab/Simulink下，设定发动机运行环境，进行仿真并记录叶片失效次数。当仿真次数很多（比如104）后，叶片失效比例就接近叶片真实失效概率。用表示第m 次仿真部件寿命，经过M 次仿真后，叶片失效概率Pfa（3490）可表示为

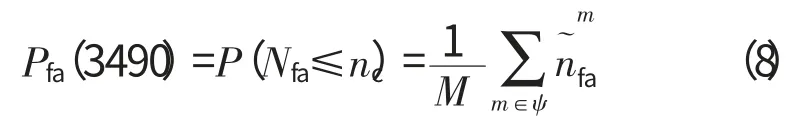
其中ψ 定义为

很难直接利用MonteCarlo仿真来实现上述方法。因为Pfa（3490）的值很小，在标称运行环境中，Pfa（3490）约为0.01%，在非标称运行环境中，Pfa（3490）也在这个数量级上。需要仿真近10000次，叶片才会出现1次失效；同时也只有这1次仿真可以用于计算失效概率，大幅度降低了仿真效率。只有仿真次数足够多时，MonteCarlo仿真的失效比例才接近于真实失效概率，仿真次数将远多于10000次。

针对上述问题，考虑到在标称运行环境下叶片失效概率容易求出，本文提出利用标称运行环境作为基准值。假设Nfa与Nfn有如下线性关系

Pfa（3490）可通过下式求得

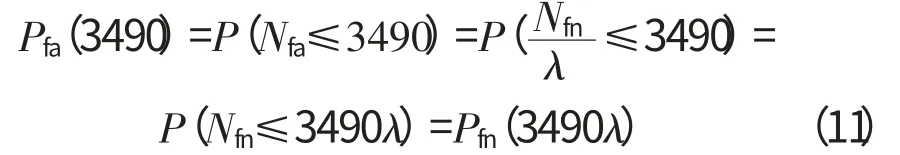
令neq=3490λ，表示非标称运行环境中的等效使用寿命。λ值已知，即可求得Pfa（3490）。由于叶片寿命Nfa为随机变量，因此λ 也是随机变量，需要利用统计法来取得λ 的估计值。将式中的Nfn用3490代替，则

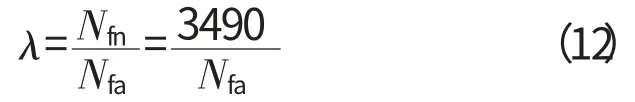
根据Nfa求出λ，利用统计知识可得

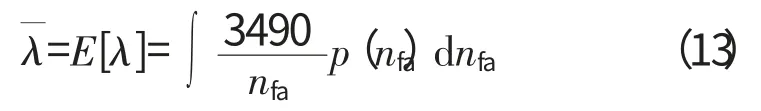
式中：p（nfa）为Nfa的分布情况，式中由于出现Nfa，因此无法直接求得，需要再次使用MonteCarlo仿真，得到

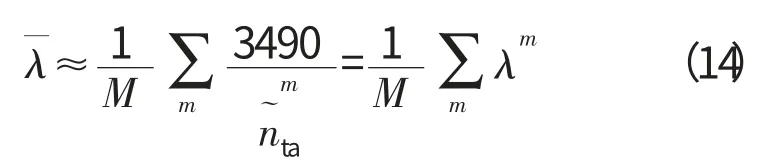
式中：λm为第m 次MonteCarlo仿真中比例系数。式（14）与式（8）的区别在于：所有的仿真均有用，可以大幅减少仿真次数，同时保证MonteCarlo仿真的准确性。具体实现步骤如下：

（1）确定仿真外部环境，如温度的变化；

（2）定义仿真次数M，另m=1:M，进行M 次仿真，收集并利用式（12）计算λm；

（3）根据式（14）计算出估计λˉ；

（4）计算出等效使用寿命neq；

（5）根据式（11）计算出非标称情况下叶片失效概率。

3 不同运行环境下叶片寿命计算

3.1 标准运行环境

这里的标准运行环境是指不考虑气候差异所导致的发动机进口温度变化，仅考虑由发动机内部噪声、材料差异所引起的叶片寿命变化。根据文献[18]，添加温度、转速、压力传感器和执行机构噪声，见表1。

表1 主要传感器及执行机构噪声

根据第2.3节中给出的方法，确定标准运行环境下与标称运行环境之间的比例系数λˉ的值。设定运行环境ALT=0km，Tin=288.15K，各参数噪声分布见表1，材料属性不确定性包含在寿命模型中。仿真5000次，结果如图3（a）、（b）所示。分别记录第m 次仿真下涡轮导叶寿命根据式（12）计算λm，再利用式（14）计算出估计。

每次计算得到的叶片总应变差如图3（a）所示，由于噪声等不确定因素，寿命模型每次计算得到的叶片总应变差均不相同，但基本分布在1个固定的范围内（0.0063~0.00655mm）。计算得到的叶片可使用寿命分布情况如图3（b）所示，计算得到λˉ=1.00636，在标称运行环境下运行3490次后，叶片等效使用寿命次循环。即在标准运行环境下运行3490次循环后，相当于在标称运行环境下运行3512次循环。

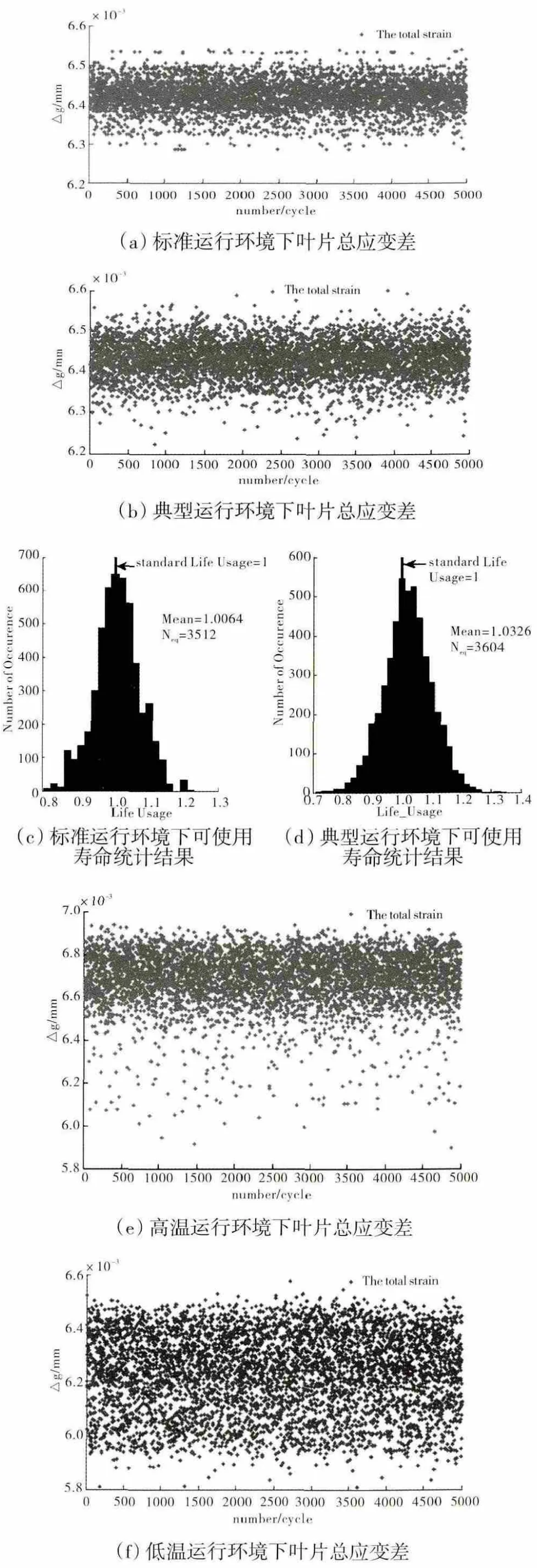
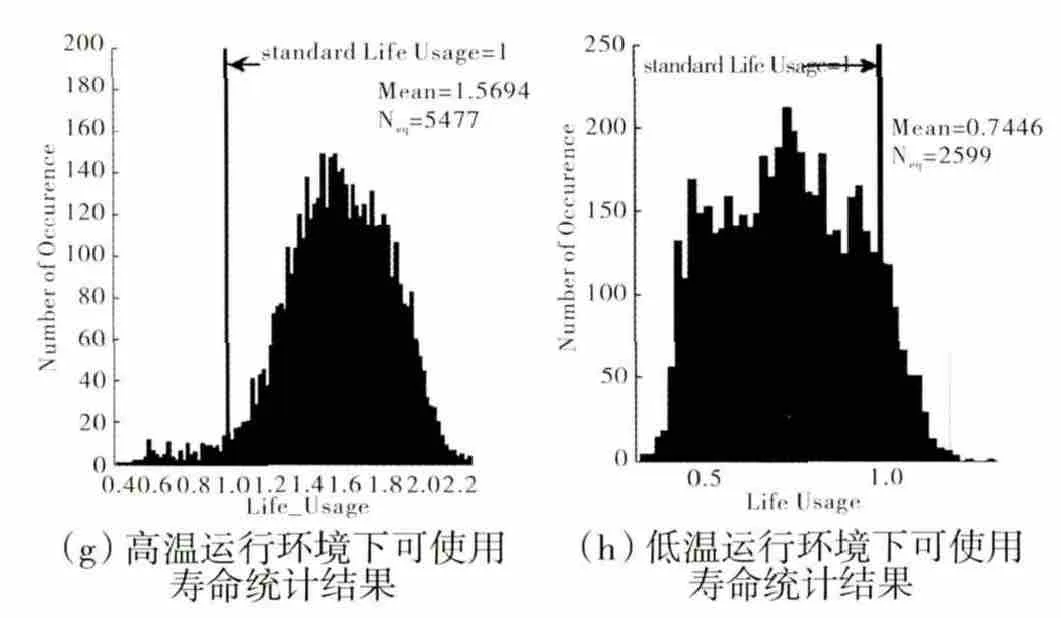
图3 不同环境下叶片总应变差及可使用寿命分析结果

则根据式（11）计算叶片失效概率

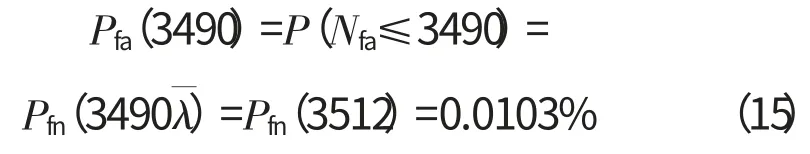
即在标准运行环境下运行3490次循环后，叶片失效概率为0.0103%。

3.2 典型运行环境

在实际使用中，很难保证飞机每次均在标准运行环境下起飞或加速，运行高度和大气温度均会变化，需要研究这些差异对寿命计算的影响。设定典型运行环境为ALT=0~1km，Tin=288.15±10K，即高度和温度在上述范围内随机变化，噪声幅值与标准运行环境下相同，其他设定同上节，其仿真结果如图3（c）、（d）所示。

在典型运行环境下，受运行高度及大气温度的变化影响， 叶片上的总应变在更大的范围（0.0062~0.0066mm）内变化，计算得到=1.0326。在典型运行环境下运行3490次后，叶片等效使用寿命为3490×=3604次循环。即在典型运行环境下运行3490次循环后，相当于在标称运行环境下运行3604次循环。

则根据式（11）得

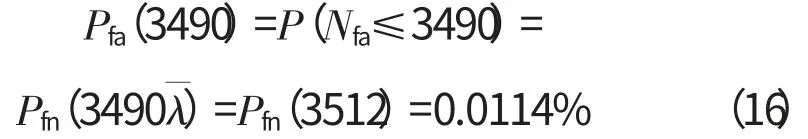
即在典型运行环境下运行3490次循环后，叶片失效概率为0.0114%。

3.3 高温运行环境

考虑到部分实际使用的飞机主要运行航线分布在近赤道附近，大部分起飞或加速时外界大气温度比典型运行环境下的高，为研究这种高温运行环境对叶片寿命的影响，设定高温运行环境ALT=0~1km，Tin=268.15±10K，噪声幅值同标准运行环境下的，其仿真结果如图3（e）、（f）所示。

在高温运行环境下，由于大气温度升高，叶片上的平均总应变比典型运行环境下的大，主要分布于0.0064~0.0070mm，此时计算得到=1.5694，这样当在高温运行环境下运行3490次后，叶片等效使用寿命为3490×=5477次循环。即在高温运行环境下运行3490次循环后，相当于在标称运行环境下运行3604次循环。

则根据式（11）

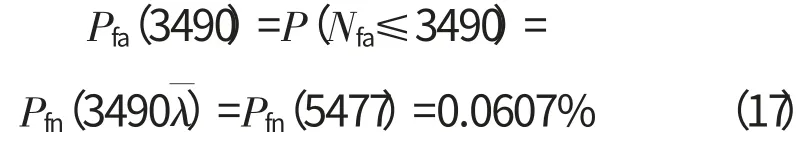
即在高温运行环境下运行3490次循环后，叶片失效概率为0.0607%。

3.4 低温运行环境

部分实际使用的飞机主要运行航线分布在近极地附近，其大部分起飞或加速时外界大气温度将比典型运行环境的低，本节中设定运行环境ALT=0~1 km，Tin=268.15±10K，噪声幅值同标准运行环境下的，研究这种低温运行环境对叶片寿命影响的仿真结果如图3（g）、（h）所示。

在低温运行环境下，由于大气温度下降，叶片上的平均总应变要比典型运行环境下的小，主要分布于0.0059~0.0065mm，此时计算得到λˉ=2599，当在低温运行环境下运行3490次后，叶片等效使用寿命为次循环。即在低温运行环境下运行3490次循环后，相当于在标称运行环境下运行2599次循环。

则根据式（11）得

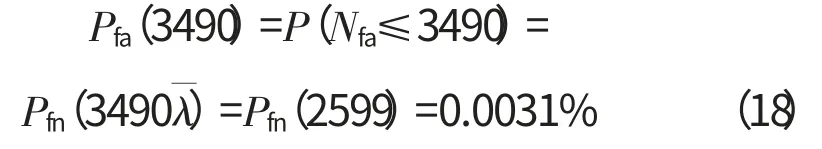
即在低温运行环境下运行3490次循环后，叶片失效概率为0.0031%。

不同运行环境下叶片失效概率及3490次循环等效使用寿命见表2。

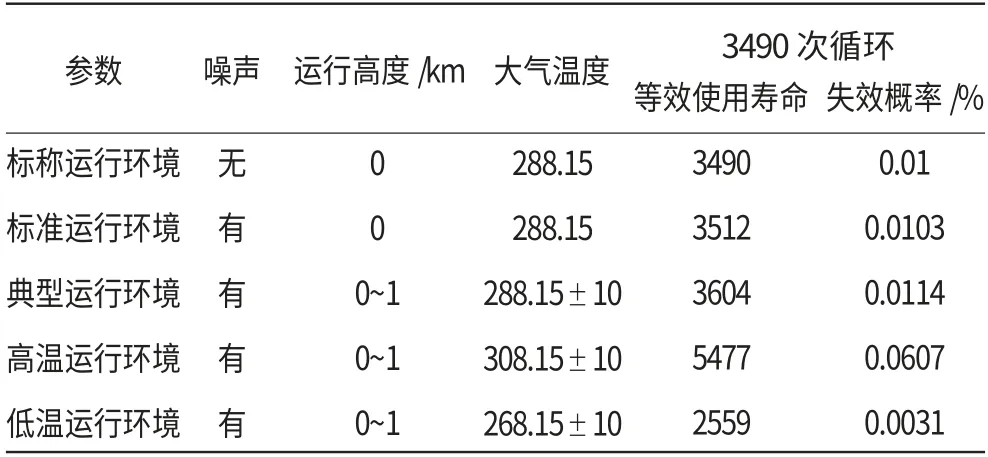
表2 不同环境下叶片寿命及失效概率

从表2中可见，在标称运行环境下，不考虑噪声影响，当运行循环数为3490次时，叶片失效概率为0.01%；而在考虑噪声等不确定因素影响的标准运行环境中，运行同样循环数，叶片失效概率增大至0.0103%；在典型运行环境中，由于运行高度及大气温度的变化，叶片等效使用寿命增加至3604次循环，此时运行3490次循环后叶片失效概率为0.0114%；而在高温运行环境下，等效使用寿命高达5477次循环，叶片失效概率为0.0607%，但在冷天环境下，运行3490次循环仅相当于在标称运行环境下运行2559次循环，因此其3490次循环叶片失效概率仅为0.0031%。

4 结论

本文利用MonteCarlo仿真和统计学理论中的威布尔分布分析了部件在各种运行环境中的寿命及失效概率，为航空发动机寿命延长控制研究提供了包含运行环境信息的部件寿命计算模型，从而在全寿命期实现寿命延长控制。主要结论如下：

（1）仿真结果显示，运行环境不确定使叶片计算寿命有大幅度变化，单纯将某一固定值作为发动机部件的安全寿命是不合理的。

（2）计算结果表明，不考虑和考虑噪声等不确定因素下，涡轮叶片失效概率相差3%；高、低温环境下，对涡轮叶片寿命及失效概率都有很大影响。

该方法可扩展到实际叶片负载和加速循环不确定性影响研究中，为发动机寿命监视提供更加准确的部件使用寿命估计值。同时也可以根据该估计值来调整寿命延长控制策略，尽可能延长部件寿命。

[1]陈小磊，郭迎清，杜宪.航空发动机全寿命期自适应寿命延长控制[J].推进技术，2013，31（1）：107-114.CHEN Xiaolei，GUO Yingqing，DU Xian.Adaptive life extending control of aircraft engine in the whole life[J].Journal of Propulsion Technology，2013，31（1）：107-114（in Chinese）.

[2]陈小磊，郭迎清，张书刚.航空发动机寿命延长控制综述[J].航空发动机，2013，39（1）：17-22.CHEN Xiaolei，GUO Yingqing，ZHANG Shugang.Summary of life extending control for an aeroengine[J].Aeroengine，2013，39（1）：17-22.（in Chinese）

[3]Vittal S,Hajela P,Joshi A.Review of approaches to gas turbine life management[R].AIAA-2004-4372.

[4]刘廷毅.航空发动机研制全寿命管理研究及建议[J].航空发动机，2012，38（1）：1-6.LIU Tingyi.Research and suggestion of life cycle management for aeroengine development[J].Aeroengine，2012，38（1）：1-6.（in Chinese）

[5]苏清友，孔瑞莲，陈筱雄.航空涡喷、涡扇发动机主要零部件定寿指南[M].北京：航空工业出版社，2004：89-97.SU Qingyou,KONG Ruilian,CHEN Xiaoxiong.The life guide of the main parts of aviation turbojet and turbofan engine[M].Beijing：Aviation Industry Press，2004：89-97.（in Chinese）

[6]Suarez E L，Duffy M J，Seto D，et al.Advanced life prediction systems for gas turbine engines[R].AIAA-2003-4985.

[7]Zhang J.Fatigue life prediction under random loading using distributional stress-life relationship[R].AIAA-99-1600.

[8]Hsiung H C，Dunn A J，Loh D L.Stress analysis and life prediction of gas turbine blade[R].AIAA-88-3218.

[9]蔡向晖，东岩，李伟.航空发动机单机技术状态寿命控制及应用[J].航空发动机，2009，35（4）：16-19.CAI Xianghui，DONG Yan，LI Wei.Life control and application of aeroengine for single engine technical condition [J].Aeroengine，2009，35（4）：16-19.（in Chinese）

[10]Grelotti R A，Glanovsky J L.Usage-based life prediction and fleet anagement for gas turbine engines[R].AIAA-2010-2972.

[11]陈小磊，郭迎清，陆军.基于修改加速控制规律的航空发动机寿命延长控制[J].航空动力学报，2011，26（9）：2116-2121.CHEN Xiaolei，GUO Yingqing，LU Jun.Life extending control of aircraft engine based on adjusting acceleration schedule[J].Journal of Aerospace Power，2011,26（9）：2116-2121.（in Chinese）

[12]凌丹.威布尔分布模型及其在机械可靠性中的应用研究[D].成都：电子科技大学,2011.LING Dan.The application of Weibull distribution model in mechanical reliability[D].Chengdu：University of Electronic Science and Technology,2011.（in Chinese）

[13]薛向珍，李育锡，王三民.某直升机主减速器传动系统的寿命与可靠性计算方法[J].航空动力学报，2011，26（3）：635-641.XUE Xiangzhen，LI Yuxi，WANG Sanmin.Method of lifetime and reliability of some helicopter's main reducer[J].Journal of Aerospace Power，2011，26（3）：635-641.（in Chinese）

[14]余国林.小子样飞机系统使用可靠性评估方法研究与应用[D].南京：南京航空航天大学,2005.YU Guolin.Study and application of the evaluation technology on the small sample aircraft system operational reliability[D].Nanjing：Nanjing University of Aeronautics and Astronautics，2005.（in Chinese）

[15]航空发动机设计手册总编委会.航空发动机设计手册（第18册）：叶片轮盘及主轴强度分析[M].北京:航空工业出版社,2001：205-235.Editorial Board of Aeroengine Design Manual.Aeroengine design manual（section 18）：strength analysis of vane wheel and spindle[M].Beijing：Aviation Industry Press，2001：205-235.（in Chinese）

[16]Liu J S.Monte Carlo strategies in scientific computing[M].New York:Springer,2008：53-57.

[17]肖刚，李天柁，余梅.动态系统可靠性仿真的五种蒙特卡罗方法[J].计算物理，2001,18（2）:173-176.XIAO Gang，LI Tianduo，YU Mei.Five Monte Carlo methods for simulation of dynamic reliability system [J].Chinese Journal of Computation Physics，2001,18（2）:173-176.（in Chinese）

[18]Behbahani A，Semega K.Sensing challenges for controls and PHM in the hostile operating conditions of modern turbine Engine[R].AIAA-2008-5280.