薄板结构畸变模型的动力学相似设计及几何区间确定

罗 忠，朱云鹏，韩清凯，王德友，刘永泉

（1.东北大学机械工程与自动化学院，沈阳110819；2.大连理工大学机械工程学院，辽宁大连116023；3.中航工业沈阳发动机设计研究所，沈阳110015）

0 引言

薄板类结构是工程中的常用构件形式，一般将板的最小宽度为板厚度的5～80倍称为薄板。薄板类结构的振动特性试验研究非常重要，但由于对原型本体进行试验会受到试验条件以及成本等多方面因素的限制，所以采用模型试验。在设计相似试验模型时，由于存在原型本身结构复杂以及尺寸参数多等，很少采用完全几何相似的模型（如航空发动机叶片材料特殊且带扭形，其原理试验常常用普通材料的直板叶片来完成），所以不完全几何相似模型即畸变模型的应用更为广泛，但不是任意畸变模型都可以用来预测原型的振动特性。学者们做了很多关于板类结构振动试验模型的研究。Simitses等[1-2]利用平衡方程建立了畸变模型的相似关系；Ungbhakorn等[3-4]建立了对称及反对称铺层的复合材料层合板固有频率与临界载荷的完全及不完全相似关系；Rezaeepazhand等[5-6]阐述了畸变模型相似适用区间的重要性，并在完全相似条件下对不同材料层合板的1阶频率的适用区间进行研究。然而，针对板类结构较高阶次固有特性预测的畸变模型设计方法，及其畸变试验模型几何区间研究的文献尚不多见。

本文对不同板类结构的不完全相似关系进行归纳比较，并以薄板为例，给出畸变试验模型几何区间的确定方法。

1 几类结构板的基本理论

单层弹性薄板、复合材料层合板、涂层板和夹层板等是几种常用板类结构。复合材料层合板是由2层或多层简单层板黏合固化在一起，作为1个整体进行工作的结构单元；涂层板是通过对表面进行性能优化，从而实现提高材料表面性能和结构性能的板类结构；夹层板是由上下2块薄的高强度表层板和填充其中的软而轻的中间夹心层所组成的板类结构。这几种板类结构都不同程度应用于航空航天领域[7]。

1.1 基本假设对比

不同悬臂板结构如图1所示。在图中，a 为板长度，b 为板宽度，h 为板（基板）厚度，th-L为层合板单层厚度，th-C为涂层厚度，th-S为表层板厚度。

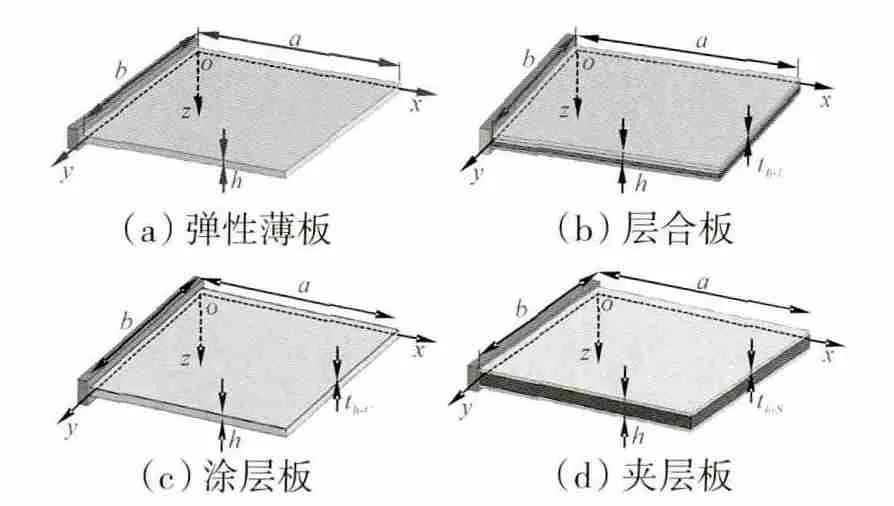
图1 不同结构板

对板类结构的研究主要基于Kirchhoff和Reissner 2种假设，其对比见表1。

表1 Kirchhoff和Reissner假设对比

一般来说，为了简化分析，4类薄板均可视为弹性板，均采用Kirchhoff假设。但在大多情况下，由于夹层板的夹心为柔性材料，按柔性板处理，即常采用Reissner假设。2种假设的具体基本特点见表2。在对夹层板的分析中，还包括Hoff假设、波鲁沙可夫-杜庆华假设等，这些理论可以看作是针对不同问题的Reissner假设的修正。本文针对板类结构固有特性问题，只采用Reissner假设对夹层板进行分析。

表2 不同结构板的基本假设对比

1.2 平衡方程对比

不同结构板的动力平衡方程在形式上存在差异，结构越复杂，其平衡方程的形式也越复杂。本文根据平衡方程分析法推导板类结构的相似关系。

（1）弹性薄板平衡方程

如图1（a）所示，根据Kirchhoff假设，薄板平衡方程[8]为

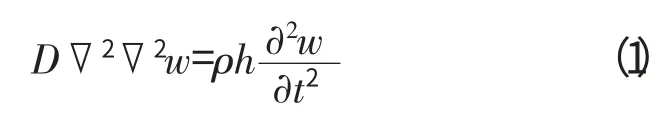
（2）复合材料层合板平衡方程

如图1（b）所示，复合材料层合板的平衡方程[9]为

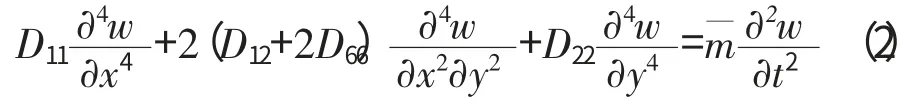
式中：D（isi=1，2，6；s=1，2，6）为各层弯曲刚度为单位面积质量。

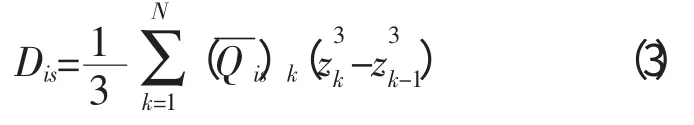
式中：zk为第k 层板与板中面的距离；（i=1，2，6；s=1，2，6）为拉伸刚度。

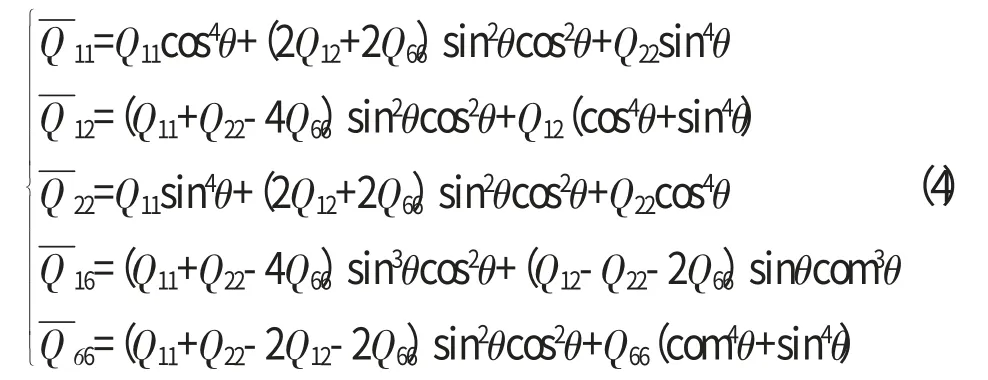
（3）涂层板平衡方程

如图1（c）所示，设涂层板的基板与涂层均为各向同性材料，则根据式（4）有

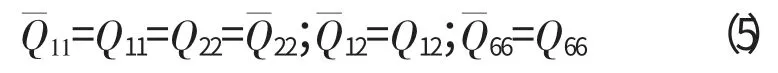
将式（5）代入式（2）得

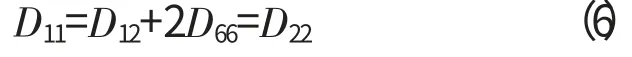
涂层板的平衡方程为

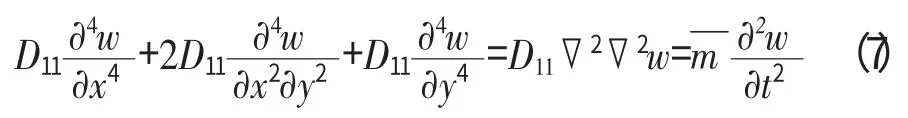
（4）夹层板平衡方程

如图1（d）所示，胡海昌提出的平衡方程简化为[10]

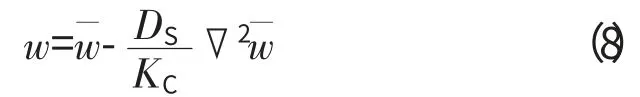
在Reissner理论下夹层板的平衡方程[11]为

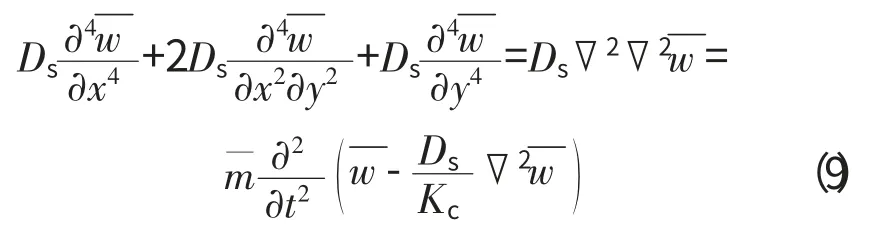
由式（1）、（2）、（7）可知，层合板与单层板的动力平衡方程的区别主要体现在刚度项不同，层合板由于各向异性材料及各层间的差异导致其各项刚度不同，涂层板可看作是特殊的层合板，其平衡方程可由层合板方程简化得到，与单层板的区别在于整体刚度不同。夹层板的方程形式与涂层板的相近，但在受力分析中考虑了夹心剪切刚度的作用，故式（9）中的w 并不代表板的挠度，而是与挠度相关的简化函数。

2 动力学相似关系

2.1 完全几何相似关系

设板上各点的振型函数为W（x，y），板挠度表示为[12]

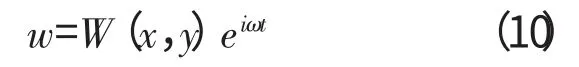
将式（10）代入式（1）、（2）、（7）、（9）得振型微分方程

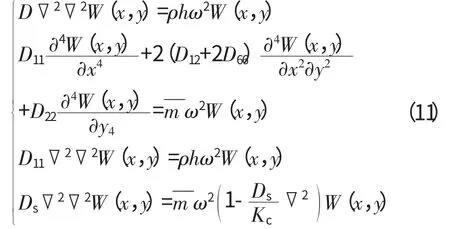
用λe表示相似关系，其中e 为各物理量的符号，如e=a，b，E 等；考虑原型与模型材料相同，有λE=λρ=1为板的等效平均密度。根据相似原理可知

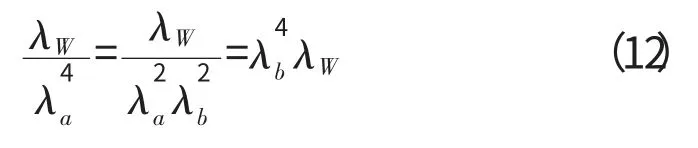
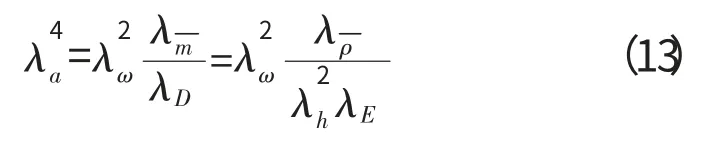
将式（13）代入式（12）得

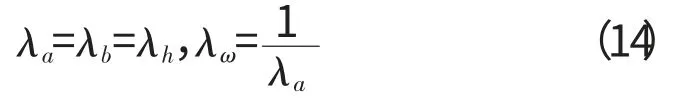
2.2 不完全几何相似关系

当完全几何相似条件无法满足时，有λa≠λb≠λh，需要新的相似关系对原型频率进行预测，设λa=Cλb，其中C 为常数，材料不同时，由平衡方程可得各类板待选的相似关系为

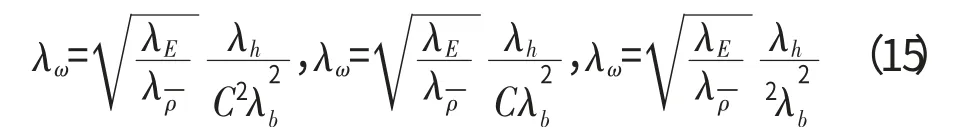
以悬臂单层弹性薄板为例，其前6阶振型如图2所示。

根据对板类结构长度及宽度的敏感性分析可知，在弯曲振动时，板长度a 的敏感性远大于宽度b 的敏感性，不完全相似关系应选择

对于扭转振动b 的敏感性大于a 的敏感性，对于高阶的混合振动，b 与a 对振动固有频率均有显著影响，这2种振型的准确相似关系计算方法较繁琐，这里只根据待选相似关系进行近似计算。对于板的扭转振动，取式（15）前2式的平均数；对于单层板/层合板/涂层板的混合振动，取式（15）后2式的平均数为

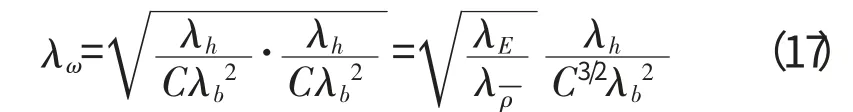
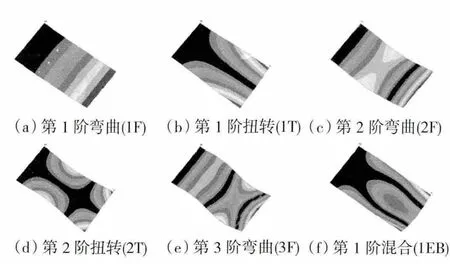
图2 悬臂板前6阶振型

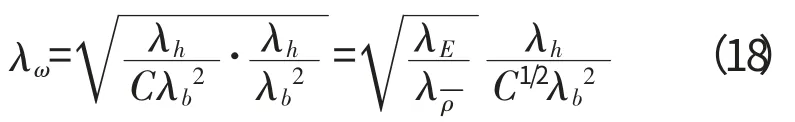
式（16）～（18）即为悬臂条件下各类板结构的近似不完全相似关系。

由于层合板、涂层板和夹层板具有比薄板更复杂的结构，在其厚度 畸变的基础上，还可能产生更复杂的模型畸变现象。

（1）复合材料层合板不完全相似关系

考虑层数不同的相似关系，以弯曲振动为例，由式（11）得

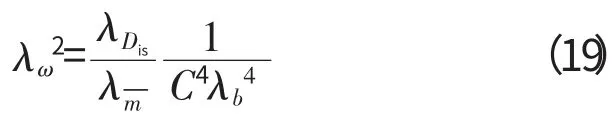
若层合板模型层数N=6，θ=0/90/0/0/90/0，由式（3）可知

由相似原理可知

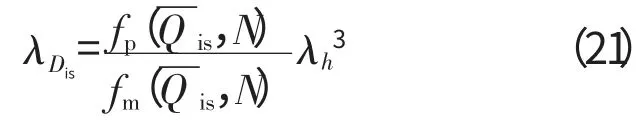
由式（3）可知

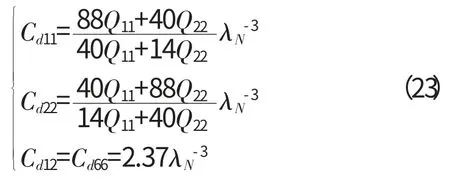
将式（23）代入式（22），再把式（22）代入式（19）可得

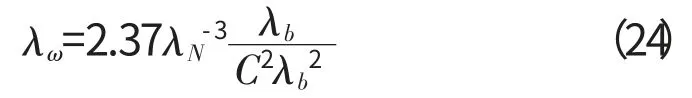
同理，对于N=2，4，可得相似关系，见表3。（2）涂层板不完全相似关系考虑涂层厚度不同的相似关系，以弯曲振动为

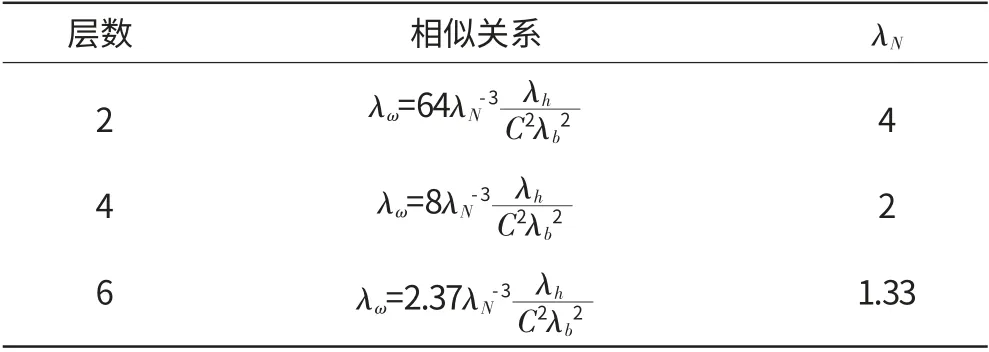
表3 N=2，4，6时的相似关系

例，由式（11）得

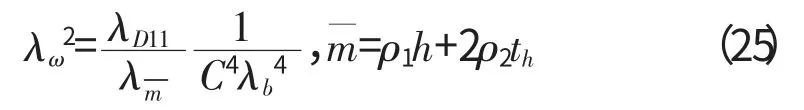
式中：ρi=（i=1，2）为基体和涂层的密度。

由式（3）得

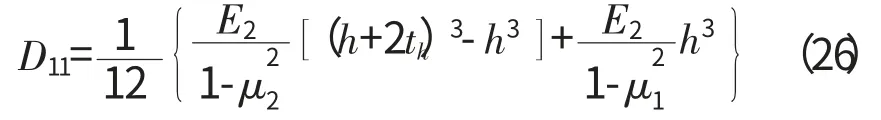
由于涂层板的涂层厚度th与基体厚度h 满足h/th，式（26）中略去高阶小量th3和th3，则有D11的相似关系为

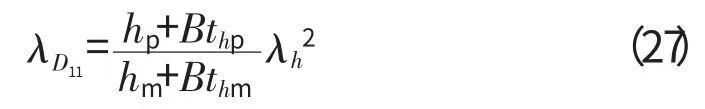
设涂层板基体与涂层的厚度之比为A=h/t，将A代入式（27）得

同理

式中：常数V=2ρ2/ρ1。

将式（28）、（27）代入式（24）得

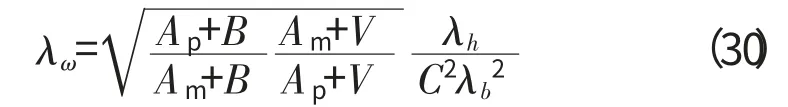
（3）夹层板不完全相似关系

考虑表层板及夹心厚度不完全相似的相似关系，以弯曲振动为例，通过式（11）得到的待选相似关系过多，难以选择，考虑Reissner理论下平衡方程[13]为

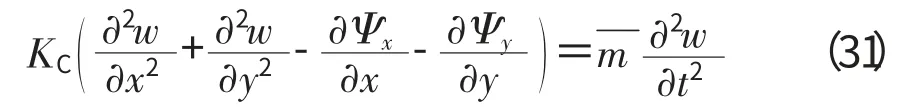
式中：Ψx、Ψy分别为夹层板弯曲时x，y 方向的偏转角；Ψx=∂u/∂z，Ψy=∂v/∂z。

由上下层板位移公式可知

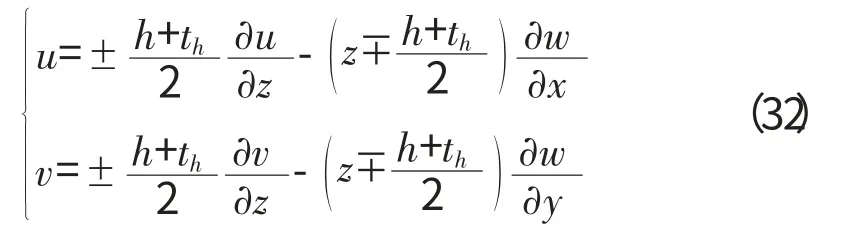
由式（32）得

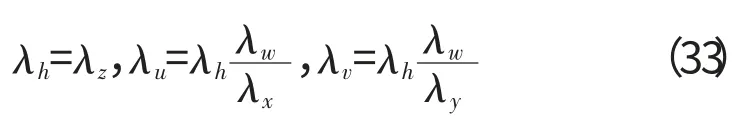
将式（33）代入式（31），由相似关系可得，弯曲振动条件下有

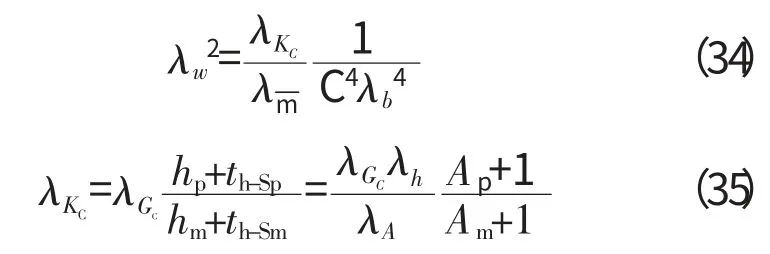
将式（35）代入式（34）得

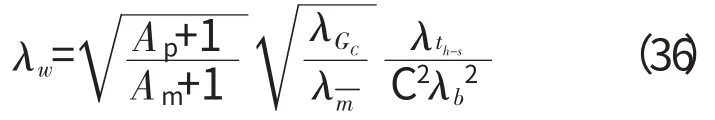
式（24）、（30）和（36）即为弯曲振动下各类板结构的畸变模型动力学相似关系，对于扭转振动及混合振动，只在式（17）、（18）前乘以与对应板结构弯曲振动相同的系数即可。

3 畸变模型的几何适用区间确定

对于动力学畸变相似模型，任何形式的不完全相似关系都有其适用范围，首先要保证原型与模型同阶振动振型相同，其次要保证其误差在允许范围内[14-15]。因此，提出几何适用区间的概念，给出板类结构几何尺寸的畸变范围。不失一般性，以悬臂条件下弹性薄板为例，给出几何适用区间的确定方法。

3.1 第1阶固有特性相似的几何适用区间确定方法

原型板为钛合金材料，其尺寸及材料参数见表3。

表3 原型板尺寸及材料参数

选取原型板：Γ=a/b=1.136，选取λb=2，λh=3，材料属性与第1部分所给原型板的相同。由ANSYS仿真分析得到原型板的第1阶固有频率ωp=155.95Hz。

在模型中选取C=[0.5，1.3，2.1，2.9，3.7，4.167]，得到对应的第1阶频率预测值ω1pr，在MATLAB中对得到的6个离散的预测值采用4阶多项式进行插值运算，得到拟合方程为

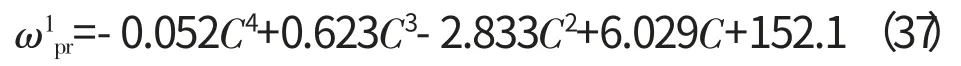
以0.05为步长选取更多的离散值对式（37）的适用性进行验证，如图3所示。

从图3中可见，在C∈[0.5，4.2]范围内式（37）具有准确的拟合效果。

对于不完全几何相似的预测误差有

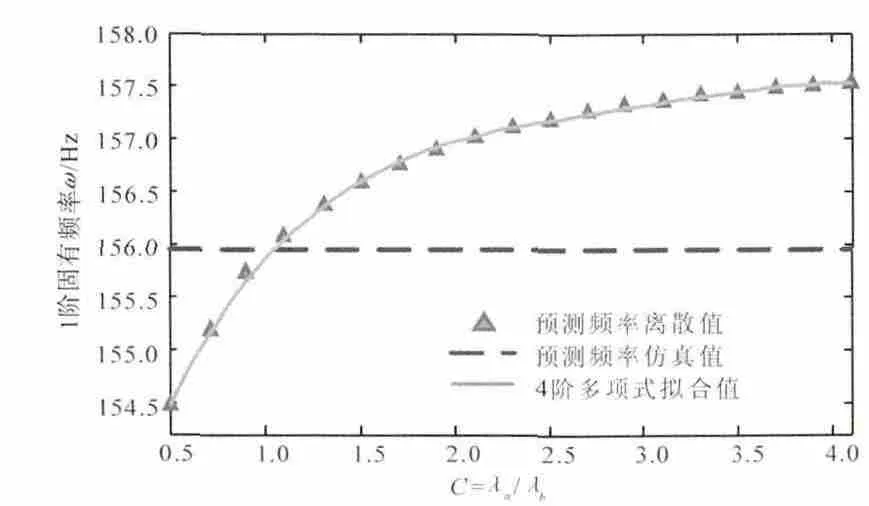
图3 4阶多项式拟合结果验证

由μ≤1%，将式（37）代入式（38）得

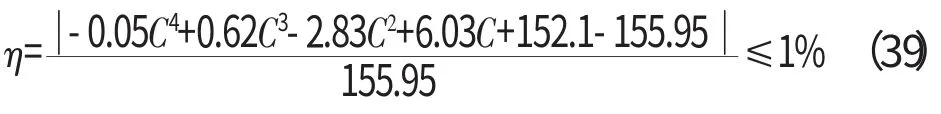
在C∈[0.5，4.2]范围内，解得Cmin=4.18，Cmax=4.18。故Γ=a/b=1.136时，几何尺寸适用区间为C ∈（0.48，4.18]。

3.2 其他阶次固有特性几何区间确定

由于几何尺寸的畸变会导致模型薄板振型的跳跃，对于文中所述原型板，使其前 阶具有相同振型的尺寸范围Γ∈[Γjmin，Γjmax]，计算得到各阶尺寸范围见表4。

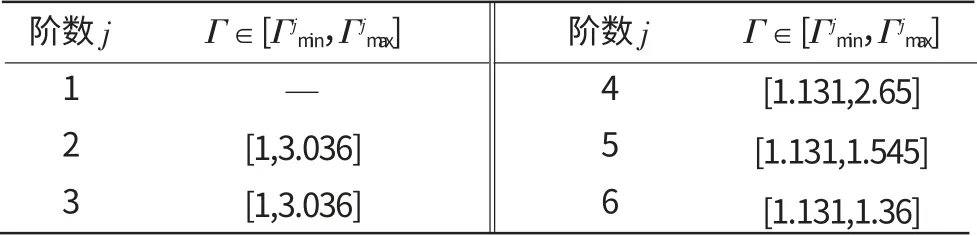
表4 各阶尺寸范围

由λa=Cλb可知，任意模型板的长宽比为

在满足模型板的高阶固有频率预测值精度的同时，还需要保证模型板振型与原型板的相同，则模型尺寸选取应满足

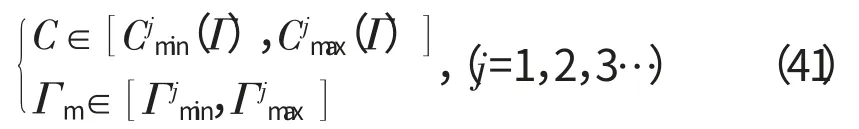
由式（40）、（41）可知，高阶固有频率的畸变模型几何尺寸适用区间为

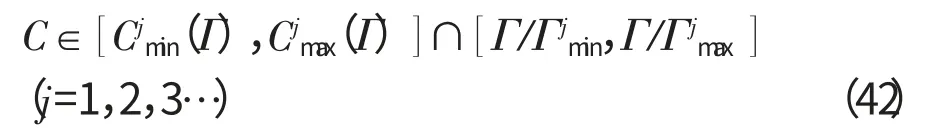
针对本文所分析的原型板尺寸，求解其第5阶固有频率的模型几何尺寸适用区间。

选 择 Γ ∈（1.131，1.545]内 离 散 点 Γ=[1.132,1.214,1.296,1.377,1.459,1.541]，分别用插值法计算其几何适用区间边界值，见表5。

表5 Γ 离散点的区间边界值

整理表5所得数据

对所得区间边界值采用3阶多项式进行插值拟合，得到

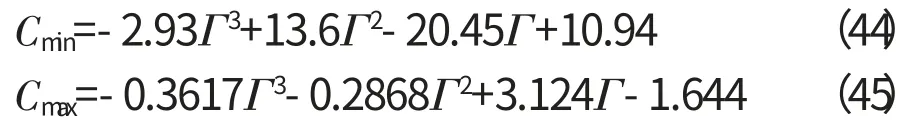
式（44）、（45）的函数图像如图4所示。

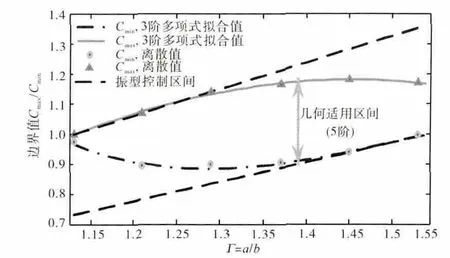
图4 5阶固有频率几何尺寸适用区间边界值

4 结论

（1）总结归纳了弹性薄板、层合板、涂层板及夹层板的基本假设的区别与联系，分别给出了不同假设下各种板类结构的动力平衡方程。

（2）利用方程分析法求解不同结构板的完全相似关系和待选的不完全相似关系，通过几何尺寸对不同振型振动的敏感性分析，给出了板类结构畸变模型的近似不完全相似关系。

（3）根据前j 阶（本文j=5）振型相同的原则，提出振型控制区间在振型控制区间内，利用2次插值法得到第1阶和高阶固有频率的几何尺寸适用区间的边界值方程。

[1]Simitses G J，Rezaeepazhand J.Structural similitude and scaling laws for laminated beam-plates [J].American Society of Mechanical Engineers,Aerospace Division，1992，26：37-45.

[2]Simitses G J，Rezaeepazhand J.Structural similitude and scaling laws for buckling of cross-ply laminated plates[J].Journal of Thermoplastic Composite Materials，1995，8（3）：240-251.

[3]Ungbhakorn V，Singhatanadgid P.Similitude invariants and scaling laws for buckling experiments on anti-symmetrically isotropic laminated plates subjected to biaxial loading[J].Composite Structure，2003，59（4）：455-465.

[4]Singhatanadgid P，Ungbhakorn V.Scaling laws for vibration response of anti-symmetrically isotropic laminated plates[J].Structural Engineering and Mechanics，2002，14（3）：345-364.

[5]Rezaeepazhand J，Simitses G J，Starnes JH.Scale models for laminated cylindrical shells subjected to axial compression [J].Composite Structure，1996，34（4）：371-379.

[6]Rezaeepazhand J，Simitses G J，Starnes J H.Design of scaled down models for predicting shell vibration response[J].Journal of Sound and Vibration，1996，195（2）：301-311.

[7]Bachynski E E，Motley M R，Young Y L.Dynamic hydroelastic scaling of the underwater shock response of composite marine structures[J].Journal of Applied Mechanics Transactions of the ASME，2012，79（1）：501-507.

[8]Soedel W.Vibrations of shells and plates（3rd edition）[M].New York:Marcel Dekker Inc Press，2004：322-336.

[9]Simitses G J.Structural similitude for flat laminated surfaces[J].Composite Structures，2001，51（2）：191-194.

[10]胡海昌.各向同性夹层板反对称小挠度的若干问题[J].力学学报，1963，6（1）：53-60.HU Haichang.On some problems of the antisymetrical small deflection of isotropic sandwich plates [J].Chinese Journal of Theoretical and Applied Mechani，1963，6（1）：53-60.（in Chinese）

[11]Carlsson L A，Kardomateas G A.Structural and failure mechanics of sandwich composites[M].New York:Springer Science and Business Media L L C London New York，2011：39-79.

[12]Qatu M S.Vibration of laminated shells and plates[M].New York:Academic Press，2004：24-39.

[13]Lee L J，Fan Y J.Bending and vibration analysis of composite sandwich plates[J].Composite and Structure，1996，60（1）：103-112.

[14]Luo Z，Sun N，Wang Y，et al.Study of vibration characteristics of the short thin cylindrical shells and its experiment [J].Journal of Vibroengineering，2013，15（3）：1270-1283.

[15]Rezaeepazhand J，Starnes JH，Simitses G J.Structural similitude and scaling laws for plates and shells：a review [C]//AIAA Structures,Structural Dynamics and Materials Conference，Tlanta，2000：393-403.