周向非均匀流动引起的转子动力学载荷分析

胡 绚，张 强，戴宏亮

（1.湖南大学机械与运载工程学院，长沙410082；2.中国飞行试验研究院，西安710089）

0 引言

在叶轮机械的工作过程中，由于受转子偏心或者上游工作级等的影响，叶轮中的流动沿周向的分布会变得非均匀，可能使叶轮转子受到附加的气动载荷，从而使其动力学性能变得不稳定，运行效率降低，甚至可能发生故障[1-3]。因此，有必要对由非均匀流动所产生的气动载荷与动力学影响进行研究，以指导叶轮机的设计与优化、提高其工作性能。

叶轮转子形心的偏移是引起周向非均匀流动的原因之一，会产生影响转子系统运动稳定性的气动载荷——Thomas/Alford力。对于转子偏心引起的气动载荷，Ehrich、Spakovszky、Martinez-Sanchez和Al-Nahwi等学者提出了不同的解析方法[2-5]，Kang等利用计算流体力学软件进行了仿真计算[6]，Storace、Martinez-Sanchez等 进 行 了 试 验 研 究[1，7]。目 前，Thomas/Alford力的产生机理已研究得比较清楚，也得到了较为统一、明确的结论。

对于由其他原因引起的非均匀流动，国内外学者更多地研究了叶轮机内部气动特性或整体性能的影响因素[8-11]；而有关叶轮结构动力学方面的研究，则主要集中于讨论叶片在非均匀来流作用下的动态特性。例如，黄典贵、陈佐一等研究了非均匀来流对叶片的气动激振力以及动叶的激振特性影响[12-14]。

本文为了研究流动的周向不均匀性所引起的、作用在轴流涡轮转子上的附加气动载荷，假设流动的周向非均匀性可以用余弦函数表示，分别考虑了非均匀来流和转子偏心的作用，也分析了偏心涡动与非稳态来流条件下转子的受载情况。

1 计算模型

1.1 模型概述

采用Song与Martinez-Sanchez的双耦合激励盘模型[2-3]，分析压气机和涡轮中由转子偏心引起的不均匀流动，以及其产生的气流激振力。该模型假设气流是无黏性且不可压缩的，也不考虑通道中的径向流动。该分析方法适用于大雷诺数的流动情况，此时流体的黏性作用相对较小，而惯性作用相对较大。在麻省理工学院所进行的偏心涡轮试验中，双耦合激励盘模型较为准确地预测了包括流动不均匀程度以及Thomas/Alford力等试验结果[3]。

在计算模型中，假设流动的周向不均匀性可以用1次谐波形式的余弦函数描述。非均匀流动的原因为：（1）周向近似呈余弦的流动是存在的。例如，叶轮转子存在偏心时，上下游的流动在忽略高次谐波小量后就可用1次谐波形式的余弦（或正弦）函数近似描述；（2）余弦形式的不均匀流动便于采用谐波分析方法得到解析结果；（3）1次谐波形式的非均匀流动是轴不对称的，因此将会产生附加气动载荷（如Thomas/Alford力）作用于转子上，可能使转子系统运动失稳。

整个分析均取叶片中径处的流动参数，任一流动参数A 可以表示为其均值A 与非均匀小扰动A'之和[16]

而其非均匀小扰动可近似地用余弦函数描述

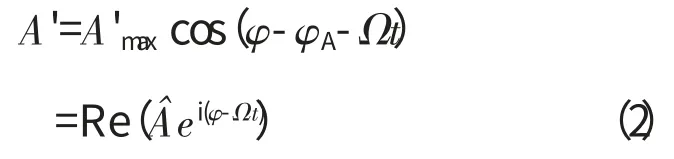
式中：A'为流动参数A 在周向位置φ 处的非均匀小扰动；A'max为扰动幅值；Ω 为转子的涡动角速度；φA是A'max相对于动坐标系n 轴的相位角；A^为复数形式的扰动幅值，包含了扰动的幅值和相位信息；Re（）表示取复数的实部。

计算模型的坐标系如图1所示。

1.2 流动的描述

由于叶顶间隙的存在，气流流经动叶时，一部分气体受到叶片引导而通过叶片通道，另一部分气体通过叶顶间隙流出。对于叶片通道主流，可以用涡轮的速度三角形来描述其流动，如图2所示。图中：c、w 分别为绝对速度和相对速度；U 为动叶中径处的线速度；α、β 分别为绝对速度角和相对速度角；x、y 表示轴向和周向。为了便于说明，图中也对各通道截面进行了编号。

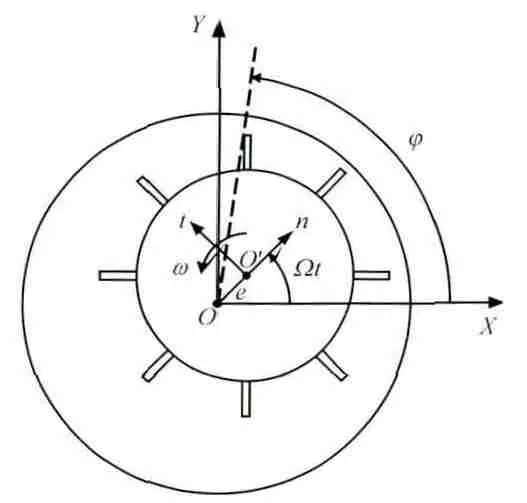
图1 计算模型的坐标系

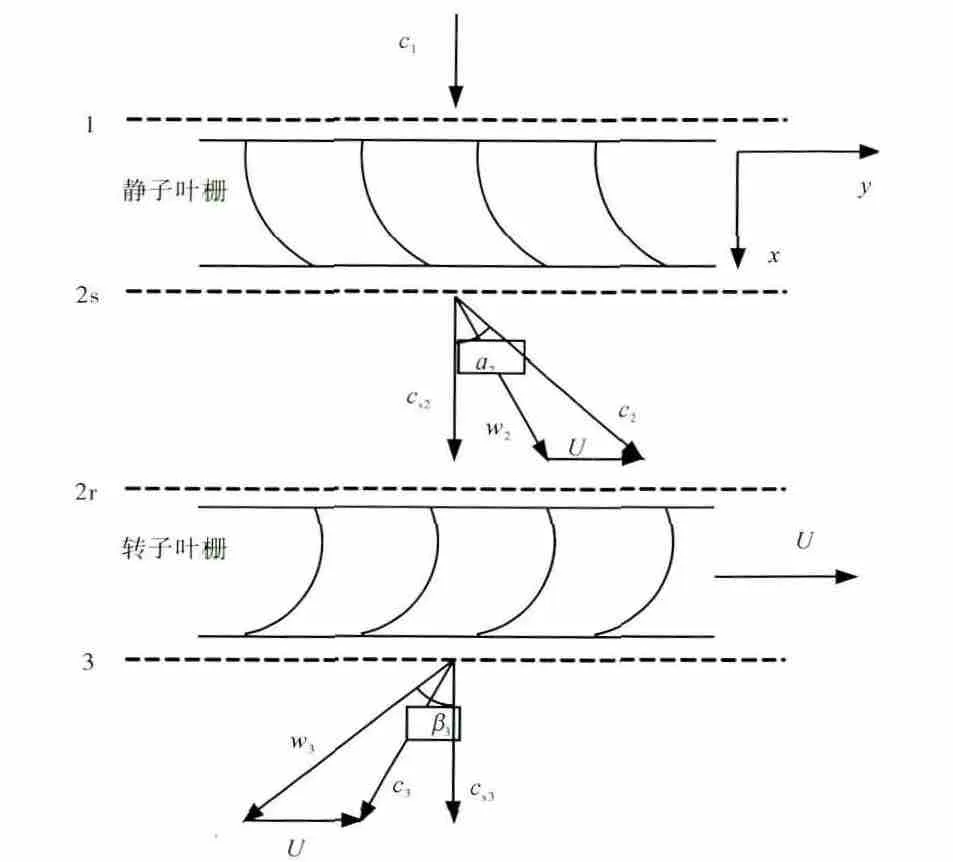
图2 速度三角形及截面编号

对于叶顶间隙流动，Song认为穿过叶顶间隙后的射流与通道主流混合形成了涡流，其流动模型如图3所示。图中：βm为动叶的平均转角；wp、ws分别为叶盆与叶背的气流相对速度；wjet为叶顶间隙射流的相对速度分别为涡流中心的相对速度和轴向绝对速度；θ 为涡流相对速度与叶片之间的夹角。通过分析动叶两侧的压差，可以给出涡流中心的相对速度角[15]

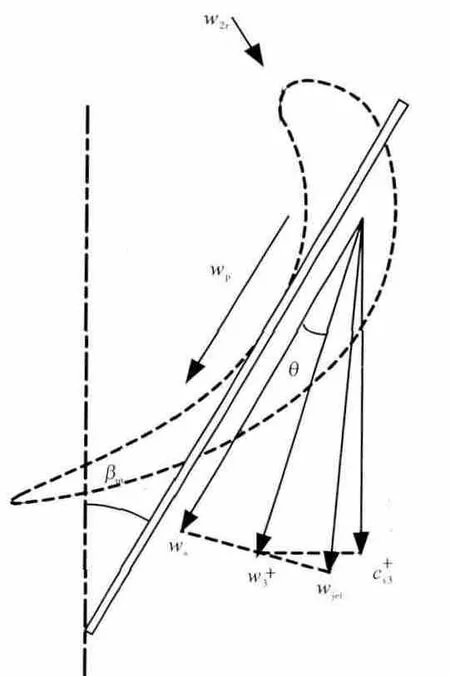
图3 叶顶间隙的流动模型

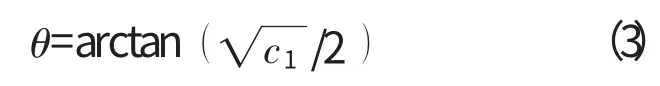
式中：c1为叶片的升力系数。

1.3 上下游流动的耦合

双耦合激励盘模型利用叶片尺度内下游无穷远处流动参数的偏导数来表示半径尺度内下游流动的小扰动，将2个尺度上的参数联系在一起，也将上下游的流动耦合在一起，其耦合关系为[16]

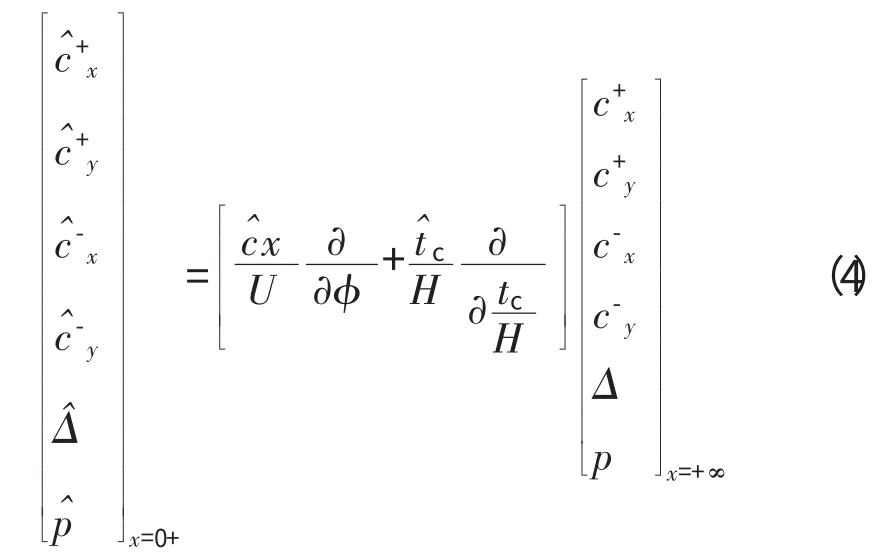
式中：Δ 为叶顶间隙流层的厚度；p 为压力；φ 为流动系数；tc为叶顶间隙；H 为叶片通道高度；上标“+”表示叶顶间隙流；“-”表示叶片通道流；x=0+、x=+∞分别表示半径、叶片尺度上的下游无穷远。

1.4 气动载荷

计算中考虑转子上的气动载荷由推动叶片运动的周向力和气体作用在转子轮毂上的压力2部分构成。

某个周向方位角φ 处叶片受到的周向气动力qy（φ）可用动量定理计算为[16]

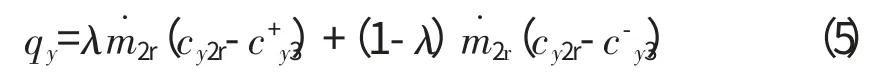
式中：λ 为叶顶间隙流量与叶片通道总流量之比；m˙2r为通过动叶的总流量。表达式的第1、2部分分别为叶顶间隙流和叶片通道流所产生的周向力。

将周向力和轮毂上的压力向转子形心进行简化，可以求得气动载荷的合力。如果通过涡轮盘的气流是周向非均匀的，转子受到的周向力或压力也会是非均匀的，那么转子形心上的合力就不为零，产生了本文所讨论的附加气动载荷。

2 算例与分析

以Martinez-Sanchez的轴流试验涡轮作为分析对象，该涡轮采用密度更大的Freon-12气体作为工作介质以减小气体黏性的影响。其设计流动系数为0.58，反力度为0.2，效率为0.79，转速为3440r/min，叶顶间隙与叶片高度之比t/H=0.02。

2.1 转子叶栅前流动非均匀的情况

由上述分析可知，通过转子叶栅的周向非均匀流动是产生附加气动载荷的直接原因。假设转子叶栅进口流动存在非均匀性，分析不同流动参数非均匀性的影响。

假设转子叶栅前的轴向速度扰动c'x2r沿周向不均匀，其无量纲为

无量纲周向力扰动为

无量纲的转子轮毂压力扰动为

式中：φ=cx/U，为流动系数。令C'x2r呈余弦分布，其幅值为0.01，最大值位于0°，所引起的周向力扰动Q'y和压力扰动P'r的周向分布如图4所示。

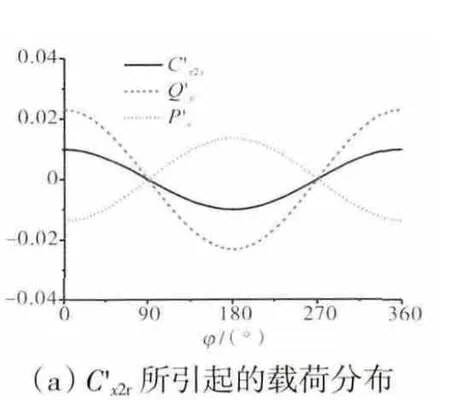
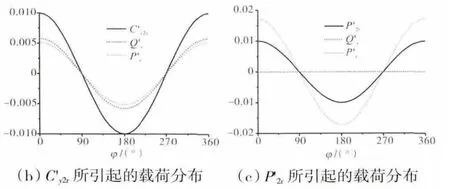
图4 C'x2r、C'y2r 和P'2r 所引起的载荷分布

若认为cx3≈cx2r，那么气体流经转子叶片通道后的周向速度为

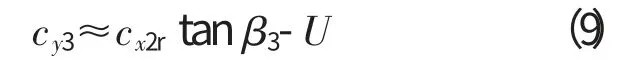
可见，在cx2r越大的位置cy3也较大，根据式（5），该位置的周向力qy随之增大。从图4中可见，Q'ymax与C'x2max的相位角相同。且在cx2r较大的位置，气体作功更多，根据伯努利方程可知，该位置的压降更多，P'rmax与C'x2max的相位角相差180°。

c'x2r、c'y2r和p'2r所引起的转子动力学载荷如图5所示。从图5中可见，因周向力与压力的不均匀分布，转子受到的附加载荷fX、fY分别为附加载荷在X、Y 方向的分量。分析非均匀周向速度cy2r的作用和引起的转子动力学载荷，根据式（6）设幅值为0.01，最大值位于0°。图4（b）给出了非均匀cy2r产生的Q'y和P'r，结果显示Q'y、P'r和C'y2r在相同位置取得最大值。

转子叶栅前非均匀压力p2r产生的Q'y和P'r如图4（c）所示。无量纲压力扰动P'2r幅值为0.01，最大值位于0°，表明p2r的不均匀性对周向力没有影响，只改变转子轮毂上压力的分布，且轮毂压力和p2r的最大值所在方位相同。非均匀p2r引起的转子动力学载荷如图5（c）所示。

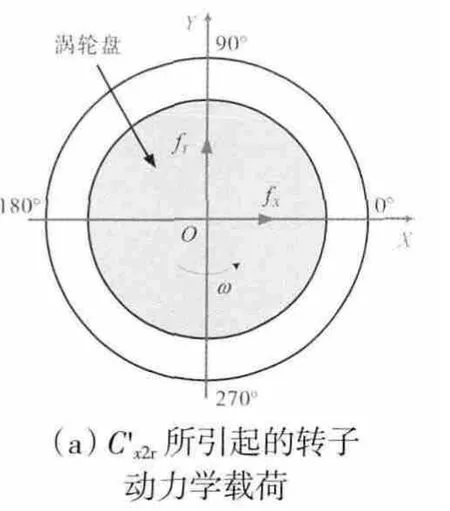
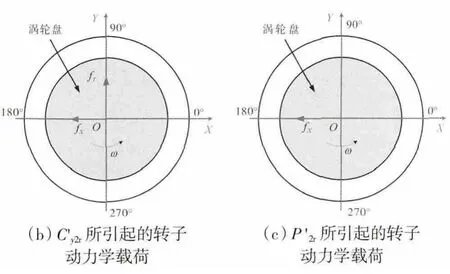
图5 C'x2r、C'y2r 和P'2r 所引起的转子动力学载荷

2.2 静子叶栅前流动非均匀的情况

静子叶栅前流动即涡轮级的进口来流，非均匀性会导致转子叶栅的流动不均匀，从而产生附加载荷作用在转子上。

设轴向速度扰动C'x1的幅值为0.01，最大值位于0°。结合速度三角形以及连续方程、动量方程可以得到截面1与2r之间的流动关系[16]，能够解得Q'y和P'r的周向分布，如图6所示。从图中可见，Q'y和P'r的分布规律与图4（a）相似，所以，C'x1和C'x2r的作用是相似的，所引起的转子动力学载荷都如图5（a）所示。

不均匀来流压力p1对流动的影响也与p2r相似，产生的附加载荷如图5（b）所示。

至于来流周向速度cy1，由于计算模型假设叶片能够完美地引导气流，因此，静叶出口的周向速度为

按照伯努利方程，静叶出口的压力为

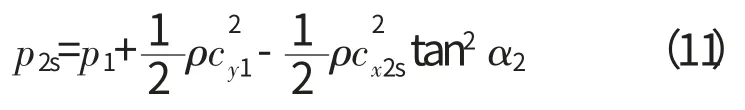
将（8）写成扰动形式，并忽略高阶小量

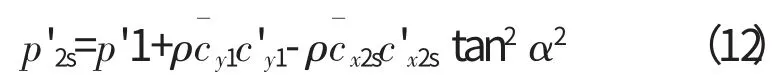
由式（10）、（12）可知，如果涡轮级来流的平均周向速度cˉy1=0，来流周向速度扰动cˉy1是不会影响cˉy2s和p'2s的，也即在双耦合激励盘模型的假设条件下，来流周向速度的非均匀性并不会引起不均匀的下游流动，当然也不会引发附加载荷，这是由计算模型的局限性所决定的。

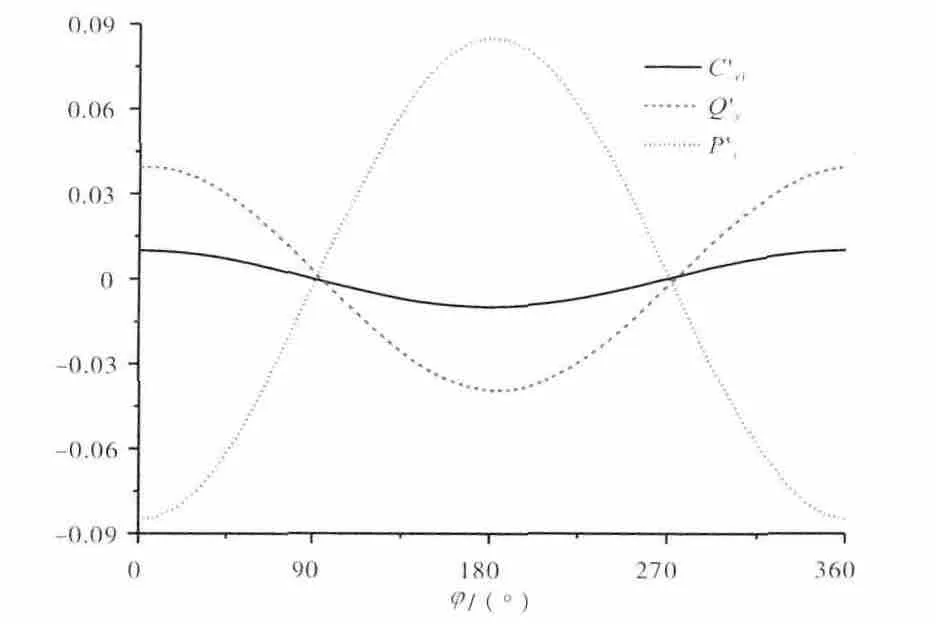
图6 c'X1所引起的载荷分布

2.3 转子静态偏心的影响

机匣变形或者转子涡动时转子形心会偏离机匣形心，使得转子叶片的叶顶间隙沿周向分布不均匀，从而产生附加载荷作用于转子。实际上，转子偏心导致气流通道发生了变化，使流动不均匀才产生了附加载荷，是由转子偏心所引起的非均匀流动。

如果转子未发生涡动，仅发生静态偏心，那么流动将是稳态的。该流动以及气动载荷已经被多位学者分析得比较清楚[15-16]，下文描述会涉及到文献[16]中的部分计算过程，以保证分析过程的连续性和完整性。

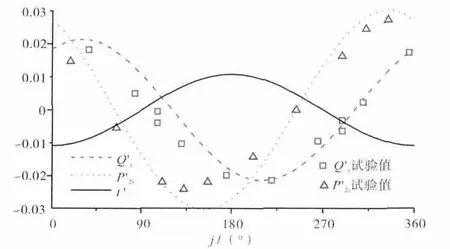
图7 静态偏心所引起的载荷分布

转子静态偏心产生的附加载荷如图8所示。fX是径向回复力，fY会加速转子正向涡动，是与转子运动稳定性相关的切向力。气动载荷系数为和αY=fY/

气动载荷与偏心距之间的线性关系如图9所示。本文的计算结果与试验值基本吻合。

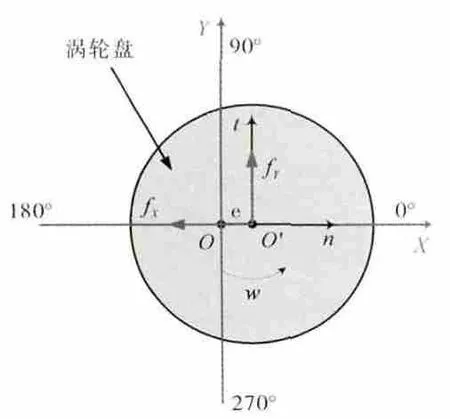
图8 转子偏心所引起的转子动力学载荷

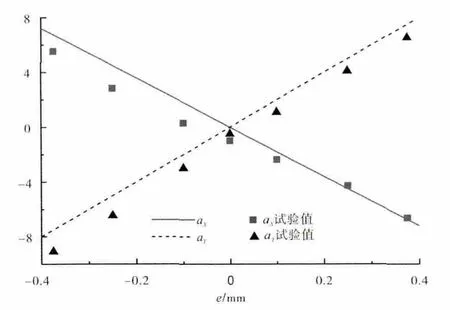
图9 气动载荷系数与偏心距的关系

理论分析和试验表明，转子的偏心除了会使下游产生非均匀来流，还会影响上游流动，使其变得不均匀，而且离转子叶栅越远，转子偏心的影响就越小。偏心转子的附加载荷fe由均匀流动通过偏心转子通道时产生的附加载荷fu和偏心引起的上游非均匀流动通过无偏心转子通道时产生的附加载荷fnonu构成。由于双耦合激励盘模型是线性的，所以2部分载荷的叠加就等于转子偏心所产生的总载荷

2.4 非稳态流动的影响

上述分析都假设流动是稳态的，下面分析转子的涡动和非稳态的来流对转子动力学载荷的影响。

对于转子发生偏心涡动时受到的附加载荷，Song已经进行了分析阐述，本文给出了与Song一致的计算结果[16]，如图10所示。图中αn和αt的定义与αX和αY相同，只是对应的是动坐标系nO't。从图中可见，无论是正向涡动还是反向涡动，2个气动载荷系数的符号都没有变化，表明附加载荷在动坐标系中方向不变。另外，αn对涡动角速度并不敏感，而αt随Ω 的增大而减小。

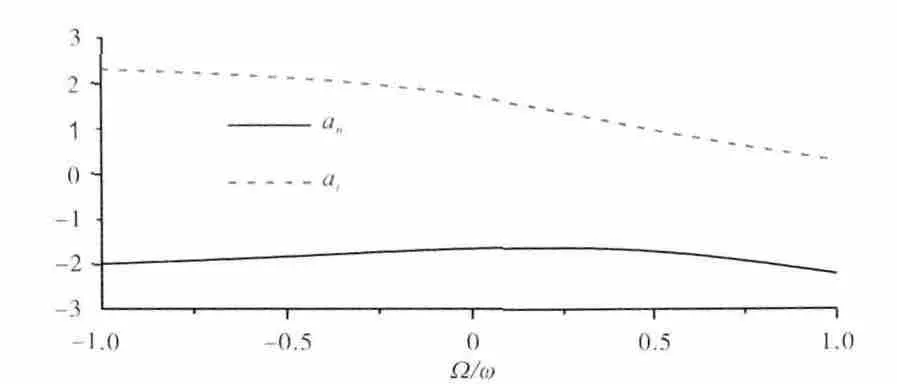
图10 转子偏心时气动载荷系数与涡动角速度的关系

对于多级涡轮，当上游的涡轮级发生偏心涡动时，其出口的流动是旋转变化的，则下1级涡轮的进口流动会变为非稳态。假设涡轮级的来流轴向速度是与时间相关的变量，令其扰动的表达式为

式中：Ω 为c'x1旋转变化的角速度，也即cx1发生周期变化，同时假设动坐标系nO't 与c'x1同步旋转。

非均匀来流所产生的附加载荷与旋转角速度之间的关系曲线如图11所示。首先，在动坐标系nO't中，αn和αt的符号不会变化，说明载荷的方向不变，fn指向cx1最大值所在方位（即n 轴正方向），而由fn向自转角速度ω 方向转动90°就是ft的指向（也即t 轴正方向），fn和ft之间的方向关系与图5（a）一致。其次，αn和αt都随着涡动角速度的增大而增大，且成线性关系。

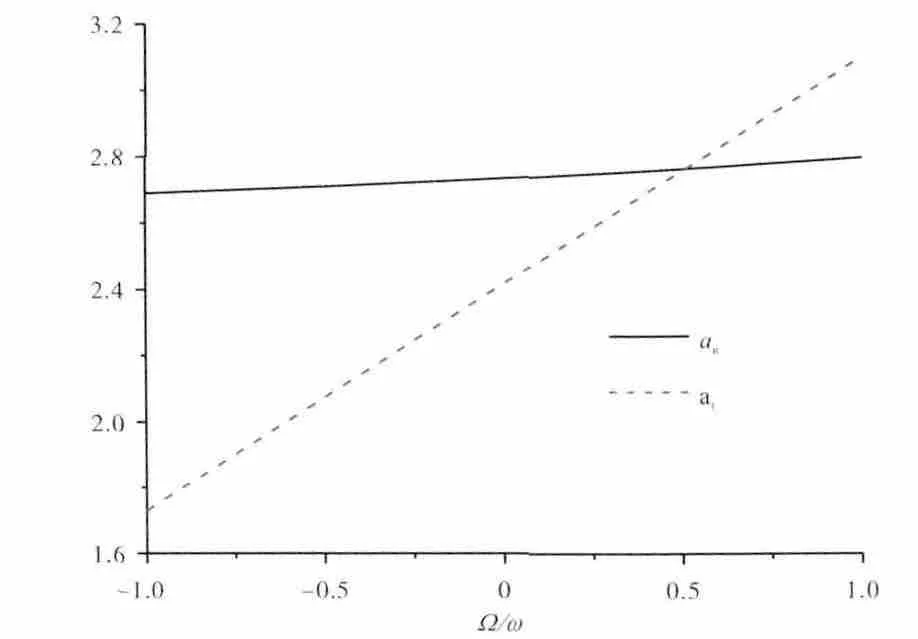
图11 来流非均匀时气动载荷系数与旋转角速度的关系

3 结论

本文运用双耦合激励盘模型，分析了轴流涡轮中1次谐波形式的非均匀流动对转子所受载荷的影响，研究了转子所受附加气动载荷的产生机理，得到的主要结论如下：

（1）1次谐波形式的非均匀流动使得涡轮转子所受气动载荷不再平衡，从而出现附加载荷，而且不同的流动参数所产生的附加载荷有所不同；

（2）发生在转、静子叶栅前的非均匀流动对附加载荷的影响是相似的；

（3）转子偏心会引起非均匀流动，计算模型能够比较准确地预测转子静态偏心时的气动载荷分布和附加载荷大小；

（4）在同步旋转的动坐标系中，涡动角速度或者来流旋转角速度并不影响附加载荷的方向，而只改变附加载荷的大小。

[1]Storace A F，Wisler D C，Shin H W，et al.Unsteady flow and whirl-inducing forces in axial-flow compressors（Part I-experiment）[J].Journal of Turbomachinery，2001，123（3）：433-445.

[2]Song S J，Wisler D C，Ehrich F F，et al.Unsteady flow and whirl-inducing forces in axial-flow compressors（Part II-analysis）[J].Journal of Turbomachinery，2001，123（3）：446-452.

[3]Song S J.An investigation of tip clearance flow excitation forces in a single-stage unshrouded turbine[D].Boston：Massachusetts Institute of Technology，1995.

[4]Al-Nahwi A A，Paduano JD，Nayfeh SA.Aerodynamic-rotordynamic interaction in axial compression systems（Part I-modeling and analysis of fluid-induced forces）[J].Journal of Turbomachinery，2003，125（3）：405-415.

[5]Al-Nahwi A A，Paduano J D，Nayfeh S A.Aerodynamic-rotordynamic interaction in axial compression systems（Part II-impact of interaction on overall system stability）[J].Journal of Turbomachinery，2003，125（3）：416-424.

[6]Kang Y S，Kang SH.Prediction of the fluid induced instability force of an axial compressor [C]//ASME FEDSM,Miami： ASME，2006：337-344.

[7]Martinez-Sanchez M，Jaroux B Song S J，et al.Measurement of turbine blade-tip rotordynamic excitation forces[J].Journal of Turbomachinery，1995，117（3）：384-392.

[8]Hynes T P，Greitzer E M.A method for assessing effects of circumferential flow distortion on compressor stability[J].Journal of Turbomachinery，1987，109：371-379.

[9]陶立权，孙鹏，杨坤.风扇/压气机进口畸变问题数值研究进展[J].中国民航大学学报，2010，28（2）：6-10.TAO Liquan，SUN Peng，YANG Kun.Development of numerical simulation methods used for fan/compressor with inlet distortion[J].Journal of Civil Aviation University of China，2010，28（2）：6-10.(in Chinese)

[10]胡骏.均匀与非均匀进气条件下多级轴流压气机性能计算--周向畸变的影响[J].航空动力学报，2000，15（3）：229-232.HU Jun.Calculation of off-design performance of multistage compressor with circum ferential distorted inlet flow [J].Journal of Aerospace Power，2000，15（3）：229-232.(in Chinese)

[11]Hermanson K S，Thole K A.Effect of inlet conditions on endwall secondary flows [J].Journal of Propulsion and Power，2000，16（2）：286-296.

[12]黄典贵.不均匀来流作用下汽轮机动叶片的动态特性分析——非定常欧拉解法[J].机械工程学报，1999，35（5）：47-49.HUANG Diangui.Analysis on dynamic characteristics of the turbine rotor blade under uneven inflow-unsteady Euler method[J].Chinese Journal of Mechanical Engineering，1999，35（5）：47-49.(in Chinese)

[13]陈佐一，吴晓峰.用振荡流体力学方法确定非均匀来流对动叶的气动激振力[J].动力工程，1999，19（2）：8-13.CHEN Zuoyi，WU Xiaofeng.Oscillating fluid mechanics method to determine unsteady aerodynamic force of rotating blades due to non-uniform inlet flow[J].Power Engineering,1999，19（2）：8-13.(in Chinese)

[14]陈佐一，霍福鹏.转子叶片在非均匀来流条件下的流体激振特性[J].发电设备，2002（2）：1-4.CHEN Zuoyi，HUO Fupeng.The fluid exited vibration properties of rotor blades under non-uniform intake flow conditions[J].Power Equipment，2002（2）：1-4.(in Chinese)

[15]Song SJ，Martinez-Sanchez M.Rotordynamic forces due to turbine tip leakage（Part I-blade scale effects）[J].Journal of Turbomachinery，1997，119（4）：695-703.

[16]Song SJ，Martinez-Sanchez M.Rotordynamic forces due to turbine tip leakage（Part II-radius scale effects and experimental verification）[J].Journal of Turbomachinery，1997，119（4）：704-713.