几类图的无符号Laplace矩阵的行列式
邱玮
几类图的无符号Laplace矩阵的行列式
邱玮
(福州外语外贸学院,福建福州 350202)
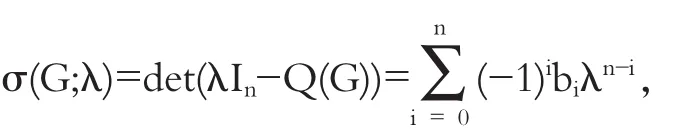
无符号Laplace矩阵;行列式;树;连通单圈图;连通双圈图
我们知道n个顶点的图G的Laplace特征值按非增排列为:λ1≥…≥λn=0,于是G的Laplace矩阵L(G)=D(G)-A(G)的行列式等于0,这里A(G)和D (G)分别是G的邻接矩阵和度对角矩阵,这是一个一般规律.那么n个顶点的图G的无符号Laplace矩阵Q(G)=D(G)+A(G)的行列式是否有确定的值?
1 图论的基本概念
定义1.1一个图是由非空点集V=V(G)和V中元素的无序对的一个集合E=E(G)所构成的二元组,记为G=(V(G),E(G)),简记为G=(V,E).边ek可以用它的两个端点vi和vj表示,记为(vi,vj)或vivj.V中的元素称为顶点,E中的元素称为边.我们用n(G)=|V|表示G的顶点数,简记为n.用m(G)=|E|表示G的边数,简记为m.对u,v∈V(G),若e=uv∈E(G),则称u和v相邻,同时也称u及v与e相关联.若e1,e2∈E (G)有一个公共顶点,则称e1和e2相邻.
定义1.2图G=(V,E)中,与顶点v相关联的边数,称为顶点v的度,记为dG(v),简记为d(v).
定义1.3图G=(V,E)中,如果两条边有相同的两端点,则称它们为重边或平行边,如果一条边的两端点相同,就称它为环.称不包含环和重边的图为简单图.本文主要讨论简单图.
定义1.4对于图G和H,如果V(H)⊆V(G),E (H)⊆E(G),则称H是G的子图,如果H是G的子图,并且V(H)=V(G),则称H是G的生成子图.
定义1.5如果图G的一个顶点和边的交替序列v0e1v1e2v2…vm-1emvm使得对1≤i≤m,边ei的两个端点是vi-1和vi,则称该序列为G的一条路径.又如果边e1,e2,…,em互不相同,则称该路径为G的一条迹(或叫链).顶点互不相同的迹称为G的一条路.路中边的条数称为该路的长度,图G中u,v两点的距离是指以u与v为起止点的u-v路的最短路长,记为dG(u,v).
定义1.6对于图G的两个顶点u和v,如果G中存在一条路,记为(u,v)路,则称u和v是连通的.如果一个图的每一对顶点都至少有一条路连结,则称该图为连通图.
定义1.7在图G中顶点的连通关系下,可将V(G)划分成有限个等价类,每个等价类构成G的子图,称为G的一个连通分支.
定义1.8圈C是指顶点集为V(C)={v1,v2,…, vn},边集为E(C)={v1v2,…,vn-1vn,vnv1}的图,记为圈Cn,n=|E(C)|为圈的长度.按n是奇数还是偶数,称Cn是奇圈或偶圈.
定义1.9没有圈的连通图称为树,记为T,每个连通分支皆为树的图称为森林.如果T为树,则n (T)=m(T)+1,这里n(T)与m(T)分别为T的顶点数与边数.
定义1.10由树添加一条边所得到的连通图称为单圈图,记为U.显然,n(U)=m(U).
定义1.11由树添加两条边所得到的连通图称为双圈图,记为W.显然,n(W)=m(W)-1.
定义1.12设图G的顶点集为V(G)={v1,v2,…, vn},用aij表示G中vi和vj之间的边数.称A(G)=(aij)n×n为G的邻接矩阵.若点vi的度为d(vi)(i=1,2,3…n),则G的度对角矩阵定义为diag(d(v1),d(v2),…d(vn) ),简记为D(G),无符号Laplace矩阵Q(G)定义为:Q (G)=D(G)+A(G).
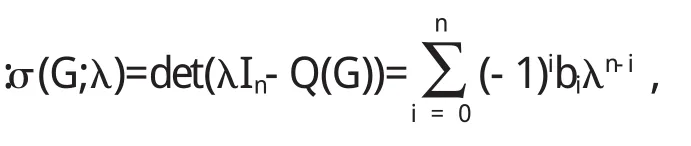
2 已有的结果
定义2.1[4,6]图G的一个生成子图称为G的TU-子图H,如果它的每个分支是树或者是非偶单圈图.
利用图G的TU-子图,Cvetkovic等[6]给出了图的无符号Laplace特征多项式的系数的一个组合解释如下:

3 本文的结果
首先我们给出n个顶点的树的无符号Laplace矩阵的行列式的值.
定理3.1设T是n个顶点的树,T的无符号Laplace矩阵为Q(T)=D(T)+A(T),则:

证明T的无符号Laplace特征多项式为:


下面我们考虑单圈图的无符号Laplace矩阵的行列式的计算问题.
定理3.2设G是n个顶点的连通单圈图,其中圈的长度为g,G的无符号Laplace矩阵为Q(G) =D(G)+A(G),则:

证明G的无符号Laplace特征多项式为:
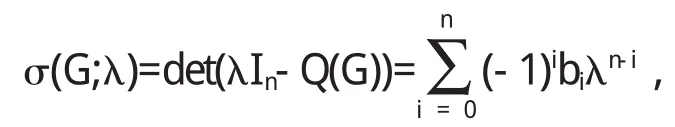


下面我们再考虑双圈图的无符号Laplace矩阵的行列式的计算问题,我们得到如下三个定理.
定理3.3设G是n个顶点的连通双圈图,其中两个圈为C1与C2,它们的长度分别为g1与g2,且C1与C2相交于一个顶点,G的无符号Laplace矩阵为Q(G)=D(G)+A(G),则:
定理3.4设G是n个顶点的连通双圈图,其中两个圈为C1与C2,它们的长度分别为g1与g2,且C1与C2不相交,C1与C2之间距离为g3,G的无符号Laplace矩阵为Q(G)=D(G)+A(G)则:

定理3.5设G是n个顶点的连通双圈图,其中两个圈为C1与C2,它们的长度分别为g1与g2,若C1与C2有公共边,且公共边的数目为g4,G的无符号Laplace矩阵为Q(G)=D(G)+A(G)则:



3.1 C1与C2相交于一个顶点,如图1.

图1 双圈图G,其中两个圈交于一个顶点
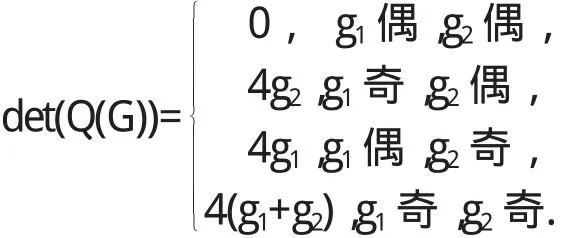
(1)当g1,g2都为偶数时,去掉任何一条边都不能形成n条边的TU-子图.根据定理2.2,det(Q(G)) =bn=0.
(2)当g1为奇数,g2为偶数时,去掉C2以外的任何一条边都不能形成n条边的TU-子图;去掉C2上的任何一条边都形成G的一个n条边的TU-子图H,此时Φ(H)=4.根据定理2.2,det(Q(G))=bn=
(3)当g1为偶数,g2为奇数时,同(2)的情况一样可得:det(Q(G))=4g1.
(4)当g1,g2都为奇数时,去掉C1,C2以外的任何一条边都不能形成n条边的TU-子图;去掉C1,C2上的任何一条边都会形成G的一个n条边的TU-子图H,此时Φ(H)=4.又因为C1,C2的长度分别为g1,g2,根据定理2.2
3.2 C1,C2不相交,且C1,C2之间的距离为g3,如图2所示.

图2 双圈图G,其中两个圈没有交点
(1)当g1,g2都为偶数时,去掉任何一条边都不能形成n条边的TU-子图.根据定理2.2,det(Q(G)) =bn=0.
(2)当g1为奇数,g2为偶数时,去掉C2以外的任何一条边都不能形成n条边的TU-子图;而去掉C2上的任何一条边都形成G的一个n条边的TU-子图H,此时Φ(H)=4.根据定理2.2,det(Q(G))
(3)当g1为偶数,g2为奇数时,同(2)情况一样可得:det(Q(G))=(-1)n4g1.
(4)当g1,g2都为奇数时,去掉C1,C2和C1,C2之间相连的边以外的任何一条边都不能形成n条边的TU-子图;去掉C1,C2上的任何一条边都会形成G的一个n条边的TU-子图H,此时Φ(H)=4;去掉C1,C2之间相连的任何一条边也都会形成G的一个n条边的TU-子图H,此时Φ(H)=4×4=16.根据定理2.2
3.3 C1,C2有公共边,且公共边的数目为g4,如图3.
(1)当g1,g2都为偶数时,去掉任何一条边都不能形成n条边的TU-子图.根据定理2.2,det(Q(G)) =bn=0.
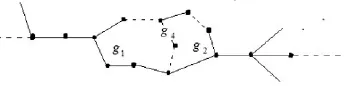
图3 双圈图G,其中任意两圈都相交
(2)当g1为奇数,g2为偶数时,去掉C2以外的任何一条边都不能形成n条边的TU-子图;去掉C2上除去公共边的任何一条边都会形成G的一个n条边的TU-子图;去掉C1,C2的任何一条公共边都会得到一个圈长为g1+g2-2g4的单圈图,由于g1为奇数,g2为偶数,g1+g2-2g4≡1(mod2),这个单圈图也是TU-子图,所以去掉C2上的任何一条边都形成G的一个n条边的TU-子图H,此时Φ(H)=4.根据定理2.2
(3)当g1为偶数,g2为奇数时,同(2)的情况一样可得:det(Q(G))=4g1.
(4)当g1,g2都为奇数时,去掉C1,C1以外的任何一条边都不能形成n条边的TU-子图;去掉C1,C2上除公共边外的任何一条边,都会形成G的一个n条边的TU-子图H,此时Φ(H)=4;去掉C1,C2的任何一条公共边都会得到一个圈长为g1+g2-2g4的单圈图,由于g1,g2都为奇数,g1+g2-2g4≡0(mod2),这个单圈图不是TU-子图,所以去掉C1,C2的任何一条公共边都不会形成n条边的TU.根据定理2.2,
综上所述,定理3.3、定理3.4与定理3.5得证.
本文主要研究n个顶点的树、连通单圈图与连通双圈图的无符号Laplace矩阵的行列式的计算问题,给出了计算这三类图的无符号Laplace矩阵的行列式的一般方法,对研究图的无符号Laplace矩阵的行列式有着重要的意义.
〔1〕王树禾.图论[M].北京:科学出版社,2004.
〔2〕孙惠泉.图论及其应用[M].北京:科学出版社,2004.
〔3〕刘缵武.应用图论[M].湖南:国防科技大学出版社,2006.
〔4〕邱玮.图的Laplace特征多项式系数的若干结果[D].集美大学,2012.
〔5〕林伟奇.树的Laplace特征多项式的系数序[D].集美大学,2011.
〔6〕Cvetkovic,Rowlinson,Simic.SignlessLaplacians of finite graphs[J].Linear Algebra and Applications,2007(423):155-171.
O151
A
1673-260X(2015)04-0004-03

