65nm工艺下MOSFET阈值电压提取方法研究

薛峰

（安徽三联学院电子电气工程学院，合肥安徽 230601）

65nm工艺下MOSFET阈值电压提取方法研究

薛峰

（安徽三联学院电子电气工程学院，合肥安徽 230601）

阈值电压Vth决定了反型沟道的建立，也就意味着MOSFET工作的开启.因此，精确地测算出阈值电压Vth是对设备特性描述的关键所在.提取阈值电压的方法很多，本文主要介绍了常数电流法、线性外推法、平方外推法、跨导线性外推法、二阶求导法和分离C-V法六种阈值电压的提取方法的原理并在65nm工艺下进行了仿真验证.本文还分析了阈值电压的温度特性和阈值电压与栅长的关系，并对这六种方法进行了总结，得出线性外推法是最简便且更准确的阈值电压提取方法.

MOSFET；阈值电压；提取方法

1 简介

阈值电压Vth决定了反型沟道的建立，也就意味着MOSFET工作的开启.因此，精确地测算出阈值电压Vth是对设备特性描述的关键所在.提取阈值电压的方法很多，然而，随着采用方法的不同，得到的Vth值不尽相同.求取Vth的各种方法主要依赖于测量单个晶体管的静态转移特性曲线Id-Vgs，多数静态转移特性曲线是在晶体管处于强反型工作区时测得的.大部分测量方法也都是在低栅压时测量的，以保证器件工作在线性区.

对于绝大多数基于Id-Vgs转移特性的Vth提取方法其共同的特点是测量得到的Vth值会受到源漏寄生串联电阻和沟道载流子迁移率降低效应的影响，这种影响对于准确提取Vth是非常不利的，因为Vth的值不应当依赖于寄生元件和迁移率降低效应.

在仿真上，阈值电压是在低Vth（小于0.1V，典型值为50mV）时，通过对Id-Vgs特性测量得到的.根据Id-Vgs的数据，有多种方法来确定Vth，如常数电流法、线性外推法、平方外推法、跨导线性外推法、二阶求导法和分离C-V法[1-2].

2 提取方法原理

2.1 常数电流法

在漏极电压小于0.1V时，与规定的漏极电流对应的栅压即为阈值电压[1,3-5]，如下式所示：

其中Ith为阈值电流，Wm、Lm分别为器件表现在掩模板上的沟道宽度以及沟道长度.由于仅需进行一次测量操作即可得到器件的阈值电压，因此，利用该方法进行测量的速度很快[1].该方法经常用于工艺监控和根据二维数值模拟（如MINIMOS）的结果确定Vth.对于上式中Ith的取值具有一定程度的任意性，无任何物理意义，这里选择Ith=10-7A，其典型值通常取值在10-6-10-9A之间[1].当选取的漏电流不同时，得到的阈值电压也各不相同，这是该方法的一个明显的缺陷.

2.2 线性外推法

该方法的本质思想是通过对Id-Vgs特性曲线的最大斜率点展开线性外推，并将外推曲线与漏电流Id为零时相应的栅极电压做为器件的阈值电压[6].其中最大斜率点对应于跨导最大的点[7-9].

通常称该阈值电压为外推阈值电压.该方法是工业界确定阈值电压Vth最为常用的标准[1-2,10].

事实上为了保证MOSFET保持在线性工作区，一般固定漏电压Vds不大于0.1V，并同时将背偏压保持在所期望的值[2,10].在低Vds时，漏电流Id（即在线性区）由下面的方程给出

该方程意义为，Id与Vgs之间是线性相关，并且与Vgs轴交于Vth+0.5αVds处[10].参数α与背偏置电压有关，一般取值范围为1.1至1.5.通常由于Vds≤0.1V，一般情况下可以假设α为1,基于这一假设引起的误差小于2%.这样以来在计算Vth值时，必须要从外推算得的取值结果中再相应地减去Vds的一半[2,10].从最大斜率点开展线性外推的理由是载流子的迁徙速率μs随Vgs增加而相应地降低，漏电流Id并不能准确地随着Vgs而线性地变化，但是从另一方面考虑，从曲线最大斜率处开展线性外推保证了不会将迁移率降低进而引起的额外误差涵盖在Vth之内[1].

2.3 平方外推法

2.4 跨导线性外推法

对于跨导线性外推法，其提取阈值电压的本质思想是：在低漏压时，跨导的微分dgm/dVgs取值最大时所对应的栅压即为阈值电压[1,9].由此方法所得到的阈值电压与公式（5）所定义的阈值电压Vth(s)非常接近，

并且它不受迁移率下降因子θ和串联电阻Rt的影响.这种方法要求器件工作在线性区，且基于以下几点结论[7]：

(1)在弱反型区，跨导和栅压呈指数关系；

(2)在强反型区，当串联电阻和迁移率退化可以忽略时，跨导为一个常量；

(3)由于串联电阻和迁移率退化的影响，跨导随着栅压缓慢增大；

(4)在弱反型和强反型的过渡区，跨导和栅压呈线性关系.

由于阈值电压是MOSFET建模，仿真和验证过程的一个非常重要的参数.人们提出了很多Vth的提取方法.在这些方法中，只有跨导增量法能够符合经典阈值电压的定义，并且消除了迁移率退化和寄生电容效应的影响.然而，由于在这种方法中需要考虑到漏电流的二级效应，跨导增量法很容易受噪声的影响.

2.5 二阶求导法

二阶求导法的提出是为了避免串联电阻对阈值电压的影响.Vth定义为跨导的导数，即

取得最大值时对应的栅压[4-7].可以通过分析理想状况下MOSFET建模时采用的一级SPICE模型来理解这种方法，即当VgsVth时，Id正比于Vgs.根据这种简单的假设，dId/dVgs是一个阶跃函数，当VgsVth时，其值为一个正的常数.因此，当Vgs=Vth时，d2Id/d2Vgs的值将趋于无穷[5].而对于一个实际的MOSFET器件，这种简化的假设显然是不准确的，当Vgs=Vth时，d2Id/d2Vgs的值不会趋于无穷，但其对应最大值.在实际的测量中，采用二阶求导法得到的阈值电压将对噪声敏感，即当考虑到噪声的影响时，测量得到的阈值电压偏大.

2.6 分离C-V法

文献[8]所提出的另一方法为分离C-V法，通常它被用于对器件反型层中迁移率的测量，同时该方法也被用于对经典阈值电压的测量，并且测量值也通常被认为是实际的阈值电压.该方法的本质是，将器件连接到栅控二极管，随后测量在准静态和高频C-V特性，并且同时测量栅和体电流，当二者电流相等，即

时对应的栅电压就是阈值电压[1].由øsi=2øf定义的Vth只适合于亚阈值或弱反型导电使得情形，而线性外推法给出的Vth是从强反型条件得到的.经典的Vth（对应于2øf）和外推法得到的Vth之间的差别大约在4Vth（～0.1V）左右.实际上，外推Vth和基于强反型条件的模型方程吻合得很好.但是采用这种方法测量阈值电压要求搭建测量电路，所以实现起来比较复杂.在器件模型仿真时，不具有可操作性.

3 仿真结果

3.1 提取方法仿真

在常数电流法中，通常选取Ith=10-7A，该值带有一定的任意性，没有任何物理含义，Ith的典型值通常是在10-6-10-9之间.当选取的漏电流不同时，得到的阈值电压也各不相同，这是该方法的一个缺陷.

用外推法计算Vth时，固定Vds=0.05V，Vgs从0V逐渐变化到最大值1.2V，同时测量对应的漏电流Id.

图1给出了采用恒定电流法和线性外推法提取阈值电压的具体做法，绿线给出的是Id-Vgs曲线，它与10-7Wm/Lm（由虚线给出）的交点所对应的栅压即为由恒定电流法测得的阈值电压.红线给出的是gm-Vgs曲线，从其最大值对应所的电流曲线上的点外延，与横坐标轴的交点所对应的栅压减去1/2Vds（这里是0.025V）即为由线性外推法测得的阈值电压.

图1 恒定电流法(CC)和线性外推法(LE)

图2给出了采用跨导线性外推法和二阶求导法提取阈值电压的具体做法，红线给出的是gm-Vgs的曲线，由其最大值处沿gm-Vgs曲线外延，与横坐标轴的交点即为由跨导线性外推法提取的阈值电压.绿线给出的是dgm-dVgs随Vgs变化的曲线，其最大值对应的栅压即为采用二阶求导法提取的阈值电压由于平方外推法不适用于短沟道器件，因此没有对平方外推法进行仿真验证.

图2 跨导线性外推法(TE)和二阶求导法(SD)

3.2 温度特性

对于NMOSFET，阈值电压的温度系数为负，即随着温度升高，n沟道MOSFET的阈值电压应当减小[11]，图3是常数电流法、线性外推法、二阶求导法和跨导增量法的温度特性.可以看出线性外推法温度系数相对稳定.

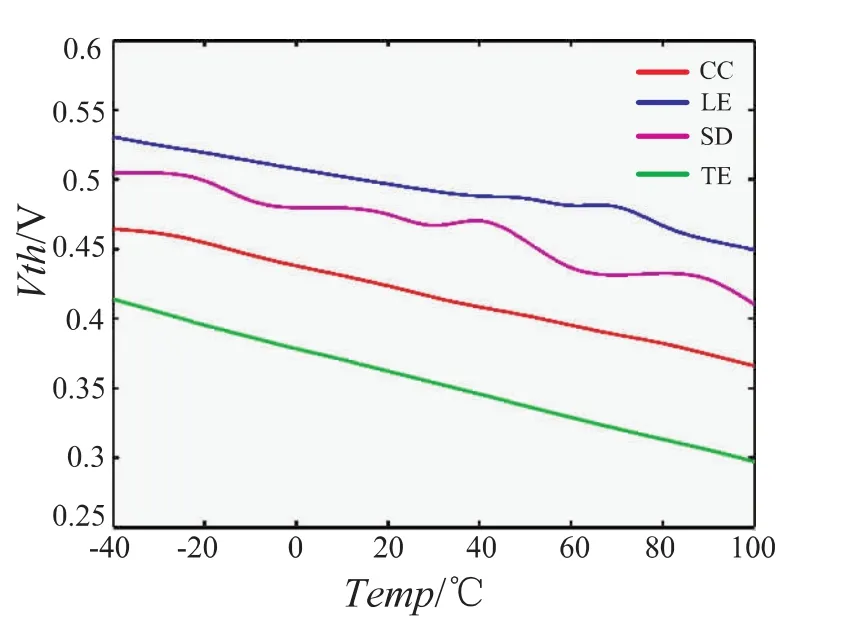
图3 阈值电压温度特性

3.3 Vth和栅长的关系

图4对比了采用恒定电流法，线性外推法，跨导增量法和二阶求导法得到的n沟道MOSFET的阈值电压随栅长的变化，由图中可以看出，在上面讨论的4种方法中，线性外推法给出的阈值电压Vth与二阶求导法的结果比较接近[12-13].

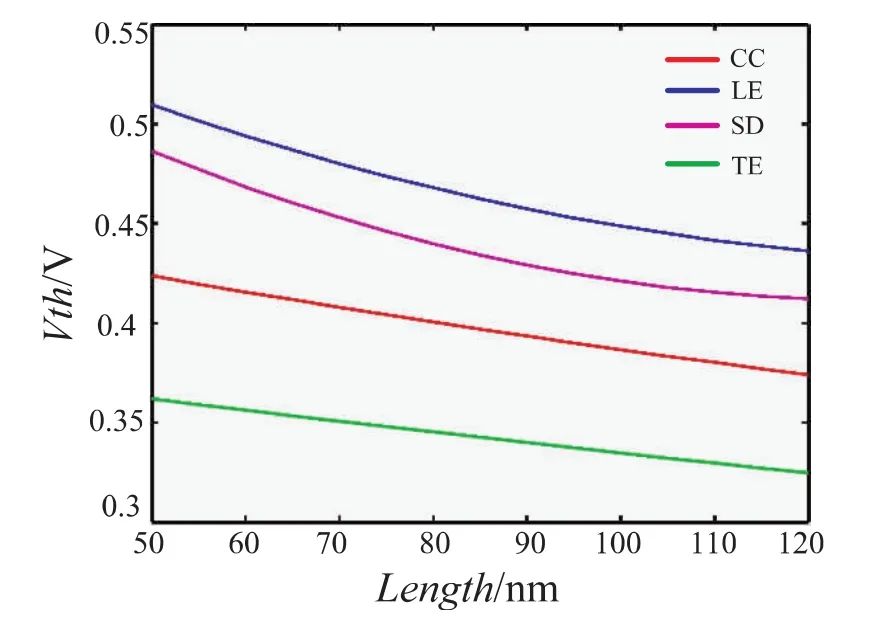
图4 阈值电压与栅长关系

4 总结

显然，上面给出的这六种方法是不等价的，得到的Vth也不尽相同.尽管利用常数电流法测量Vth最简单，并能达到合理的精度，但得到的Vth依赖于电流的选取值和亚阈值斜率；在电路中，器件一般工作于强反型区，根据强反型电流测量得到的Vth比在弱反型得到的Vth更适用于实际电路，因此利用外推法得到的Vth更为准确.线性外推法和平方外推法之间的区别在于，饱和区Id随Vth的变化会影响测量结果，但在上面的一级近似方程中并未考虑该效应；由于该效应在短沟器件非常显著，因此随着沟道长度的下降，两种外推法得到的Vth的差别会增大.对于跨导线性外推法，它所基于的理论假设在实际中并不能严格的成立，而且参数提取要求器件工作在弱反型区，这对于器件通常工作在强反型区的绝大多数电路（低功耗电路除外）也是不是实际的.而对于二阶求导法法，它需要漏电流对栅压进行两次求导，计算过程相对复杂.分离C-V法要求搭建实际的测量电路，而且必须保证测量装置具有足够高的灵敏度以测量出微小的寄生电容值，实现起来相当复杂.综上从算法难度、二级效应的影响、实际测量的可行性、温度特性和与栅长关系等方面综合考虑，我们推荐线性外推法.

〔1〕唐瑜.等离子体工艺对MOS器件的损伤研究［D］.西安电子科技大学，2007.

〔2〕董立亭.考虑量子效应的MOSFET器件模型建模及验证［D］.贵州大学，2007.

〔3〕Bazigos A，Bucher M，et al.An Adjusted Constant-CurrentMethodtoDetermineSaturatedandLinear Mode Threshold Voltage of MOSFETs［J］.IEEE Transactions on Electron Devices，2011，58（11）：3751-3758.

〔4〕Siebel O F，Schneider M C，Galup-Montoro C.MOSFET threshold voltage：Defnition，extraction，and some applications［J］.Microelectronics Journal，2012，43（5）：329-336.

〔5〕Terada K，Nishiyama K，Hatanaka K I.Comparison of MOSFET-threshold-voltage extraction methods［J］.Solid-State Electronics，2001，45（1）：35-40.

〔6〕Liou J J，Ortiz-Conde A，Sanchei F G.Extraction of the Threshold Voltage of MOSFETs：an Overview［J］. IEEE HongKong electron devices meeting，1997：31-38.

〔7〕Ortiz-Conde A，Garc？a Sánchez F J，Liou J J，et al.A review of recent MOSFET threshold voltage extraction methods［J］.Microelectronics Reliability，2002，42（4）：583-596.

〔8〕Yang H，Inokawa H.A differential smoothing technique for the extraction of MOSFET threshold voltage using extrapolation in the linear region［J］.Solid-State Electronics，2012，76：5-7.

〔9〕DobrescuL，PetrovM，DobrescuD，RavariuC. Threshold Voltage Extraction Methods for MOS Transistors［J］.International Semiconductor Conference，2000，1：371-374.

〔10〕滕浙乾.SOI/CMOS器件建模研究与模型参数提取［D］.国防科学技术大学，2010.

〔11〕Wang R，Dunkley J，DeMassa TA，JelsmaLF. Threshold voltage variations with temperature in MOS transistors［J］.IEEE Transactions on Electron Devices，1971，18（6）：386-388.

〔12〕Kong F C J，Yeow Y T，Yao Z Q.Extraction of MOSFET Threshold Voltage，Series Resistance，EffectiveChannelLength，andInversionLayerMobility From Small-Signal Channel Conductance Measurement［J］.IEEE Transactions on enectron devices，2001，48（12）：2870-2874.

〔13〕Tsuno M，Suga M，Tanaka M，Shibahara K，et al. Physically-Based Threshold Voltage Determination for MOSFET's of All Gate Lengths［J］.IEEE Transactions on Electron Devices，1999，46（7）：1429-1434.

TN432

A

1673-260X（2015）04-0046-03

安徽三联学院校级自然科学研究项目（2013Z012）