用于索网张拉结构找形的几何非线性有限元法综述
改造者:尤国强 刘 辉 胡景勤
用于索网张拉结构找形的几何非线性有限元法综述
改造者:尤国强 刘 辉 胡景勤
索网张拉结构在施加预张力之前是柔性体,只有对其施加一定的预张力后才能使其具有确定的形状和刚度。索网张拉结构的找形计算可以得到索网张拉后的形态、张力分布和结构刚度等结构性能结果。本文介绍了索网张拉结构找形的相关概念,并根据已有文献综述了用于找形计算的几何非线性有限元法的基本原理和推导过程。
索网张拉结构找形中的状态定义
在对索网张拉结构进行找形计算时,根据索张力的施加过程,可对应将索网张拉结构的形态划分为三个不同的状态阶段。
1.零状态
零状态时索网张拉结构中还未施加预张力,整个索网张拉结构可以看作仅是由一些具有给定几何尺寸和位置的索段所组成的集合体。此时结构不存在预张力,也不承受外部荷载的作用。
2.自平衡状态
自平衡状态是指索网张拉结构在自身预张力的作用下达到的力平衡状态。该状态下,索网受到沿索网展开方向的张拉作用,由未受力时的柔性体,形成具有一定形状和刚度的稳定结构。
3.外载荷工作状态
外载荷工作状态是指索网张拉结构在自平衡状态的基础上,受到外载荷(承重、风载等)作用所达到的力平衡状态。该状态可以反映出索网张拉结构的具体工作性能。
零状态下的索网是由一些柔软索段联结而成的柔性体,没有固定的形状和刚度。当对零状态下的索网沿展开方向进行张拉后,它将达到自平衡状态,此时索网内的张力在仿真计算时被当作初始预张力来处理,而初始预张力的大小决定了索网的初始形状和刚度。自平衡状态在理论上可认为是在一定结构边界约束条件和机构拓扑条件下,由索网张拉结构的几何构型和施加的初始预张力相互作用所产生的结果。只有在索网张拉结构达到自平衡状态从而具有一定的刚度后,它才能承受外部载荷,进入工作状态。
因此,为了准确分析索网张拉结构的力学性能,就需要在给定索网索段长度、预张力大小和约束条件的情况下,先计算得到索网的自平衡状态。而这个求解索网张拉结构初始平衡态的问题也就是通常所谓的索网张拉结构的找形问题。
工程上通常将索网张拉结构的找形问题分为以下三类。
1.指定拓扑形态时的索网找形问题
通常工程实际中需要索网张拉结构能够形成指定的形状,从而满足诸如大跨度屋顶或天线反射面等结构的预定形状要求。此时,需要在指定尺寸和位置的要求下,确定出索网张拉结构中索段的长度和索段内预张力值的大小。
2.指定预应力时的索网找形问题
有时为了满足结构稳定性的要求,需要索网中的预应力具有指定的合理分布状态。此时,为了满足这一指定的预应力分布要求,则需要通过找形计算,确定出索网张拉结构的拓扑形态信息。
3.指定索网零状态时的索网找形问题
当索网结构的索段长度、施加的预张力大小和拓扑形式都已经给定时,需要根据这些已知条件计算出索网张拉结构的形状和力学性能,以便进一步进行后面的外载荷分析。
指定拓扑形态时的索网找形问题是工程中最常见的找形问题。
几何非线性有限元法
从上世纪50年代末到60年代初,有限元法逐渐成为结构分析的主流方法。该方法是一种利用分片差值逼近的离散化方法。从工程和物理的角度来看,有限元法是把连续性问题转化为离散问题并进行求解的方法;而从数学角度来看,有限元法是把偏微分方程转化为代数方程并对其进行求解的方法。非线性有限元法正是在有限元法的基础上发展起来的,它可以用于求解带有非线性偏微分方程的复杂问题。
索网张拉结构的非线性特征主要体现在应变与位移的几何非线性关系上,在对索网张拉结构进行非线性有限元分析时,首先需要根据索网张拉结构的拓扑形式将其离散成若干个独立的索单元;然后以这些索单元为基础建立各索单元的刚度矩阵;接下来再根据索单元在整体结构中的位置和相互连接关系,得到整体结构的总体刚度矩阵;最后由指定的边界条件迭代求解相应的非线性有限元方程,从而得到自平衡态时的各索单元的节点位置和内力分布。
为了便于整体上的理解,下面将给出索网张拉结构几何非线性有限元分析的普遍推导过程。
在对索网张拉结构进行非线性有限元分析时,需要先做出如下假设:
1.索段被假定为只能受拉、不能受压的索杆单元;
2.索杆单元的材料特性满足胡克定律。
对于离散后的结构,由虚功原理可写出:

式中,δ{d*}T——虚位移;
δ{ ε*}T——对应于虚位移的虚应变;
{σ}——应力矩阵;
{p}——外载荷列阵。
由应变的增量形式,可得到应变和位移的关系为:

式中,[B]——应变矩阵。
上式即为增量形式的几何方程,将此式代入式(1)可得:

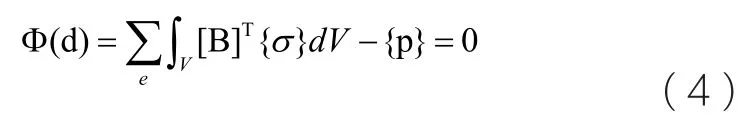
索网张拉结构中单元位移和单元应变之间的关系是非线性的,为了能够明确表达出单元应变的物理意义,这里将应变矩阵写为线性部分和非线性部分的组合形式:

[BNL]——索单元几何非线性特性引起的非线性应变部分。

另外,对于索网张拉结构而言,其材料特性仍为线性状态,即应力和应变之间仍呈线弹性关系,因此有:

式中,[D]——材料特性矩阵;
{σ0}——初应力矩阵。
由式(2)和式(7)可得:


为了求切线刚度矩阵,将上式两边对{d}取微分,可得:

将式(6)和式(7)代入上面和式中的第一项可以得到:
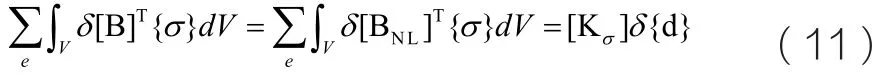
其中[Kσ]称为初应力矩阵。
再将式(8)、式(5)代入式(10)中和式的第二项可得:

其中,[Ke]和[Kg]分别称为弹性矩阵和初始位移矩阵,并有:
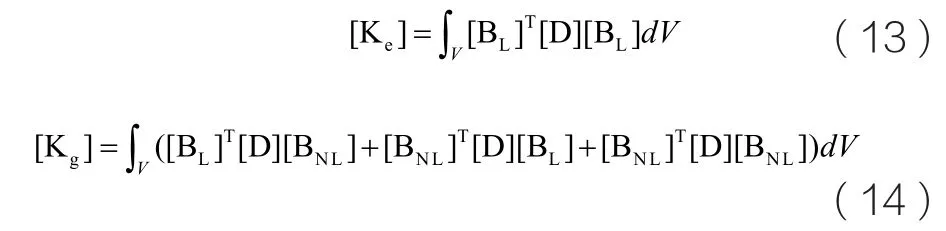
此时,平衡方程最终可写为如下形式:

上面的[KT]称为总切线刚度矩阵。
至此本文整理出了索网张拉结构的几何非线性有限元方法的推导计算过程。这些推导为索网张拉结构的找形计算提供了理论依据,并可以作为理论基础进一步进行索网张拉结构的外载荷平衡态分析计算和动力性能分析计算。

尤国强 刘 辉 胡景勤
西安翻译学院
感谢陕西省教育厅专项项目(14JK2040)和院级科研项目(BK001)对本文的资助。
10.3969/j.issn.1001-8972.2015.16.040

