利用函数迭代生成伪随机数列的方法研究

白金鑫 宋运娜

利用函数迭代生成伪随机数列的方法研究

白金鑫 宋运娜

伪随机数列以它的内在随机性、对初始条件的高度敏感性以及预先确定性和可重复性等特性，在当代的密码学、通讯、以及仿真实验等多个领域有着重要的应用。本文用实验的方法找出两个函数和迭代生成伪随机数列。并通过分析他们的图像的混沌行为，找出其生成伪随机序列的区间分别为和判断它们生成的伪随机数服从均匀分布。通过对初值加入一个小扰动ε并提取后十一位随机数做对比，证明了两个函数均对初值具有敏感性。并通过大量实验估计出函数初值的取值范围是

伪随机序列的混沌系统具有确定性系统中的内在随机性、对初始条件高度敏感、长期不可预测性、有界性等特征，这些特性被各种领域所关注，并被广泛应用到系统控制、密码学、保密通讯、信息隐藏中。真正意义下的随机数只存在数学理论中，通过计算机仿真所产生的随机数又称为伪随机数。这种内在随机性被普遍应用于密码学领域，作为产生密钥的有效机制之一。本文的目的是通过函数迭代的方法，建立一个符合均匀分布的伪随机序列的数学模型。经过多次尝试找出符合伪随机数性质的迭代函数，编写matlab程序，并画出此随机数的分布图。通过对图形的分析找出此随机序列的初值的取值范围以及常数的选取范围，并通过给定初值的小增量ε后，将前后所得的随机数做对比的方法来检验此随机序列的初值敏感性。最后给出我的猜想及结论。

实验原理

本文的实验原理是根据数学实验中混沌实验和分形实验。

设D 是实数R 的一个子集，并且又设f:D →D是一个连续映射，用fk表示函数f 的第k 次迭代，即f0（x）=x ，f1（x）=f（x），f2（x）=f（f（x）），……如果我们将函数的迭代次数k=0，1，2，…视为时刻，而在时刻k=n的函数值则是函数的第n 次迭代值，则给定迭代初值x，则会通过上面的迭代系统依次产生一个序列：

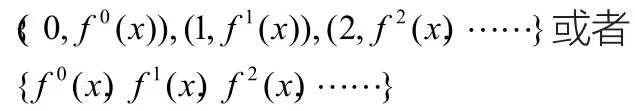
此迭代序列称为离散动力系统，对于给定的迭代初值x，此序列也称为离散动力系统的一条轨道。如果将迭代次数作为横轴，迭代值作为纵轴，就可以观察轨道的性态，不同的函数，不同的初值，会产生不同的结果。

迭代函数的选取。在此类函数中最经典的两个模型为

伪随机数对初值的敏感性分析：对于固定的函数f 及很小的ε，若初值x0与x0+ε当迭代次数足够多的时候，最终两条轨道重合（开始的时候一般不会重合），则这个随机序列发生器就没有实际的应用价值。因此，生成伪随机序列的函数f要求对初值具有敏感性，即对不同的初值，即使相差很小，都不会产生相同的序列。

实验过程

利用上述原理编写的matlab程序程序中的a1和a2为函数中a的取值范围，此处给定的初值x=0.8，a1=0，a2=30，可以得到如下图形。

发现这个函数在a取a≥5以后，y在0附近符合随机数的性质，这样我们保持初值不变，将a值区间变成15-20，将y值范围变成（-4，4），这样只需在程序中加入语句：ylim（［-4，4］）；这样得到的图形如下。

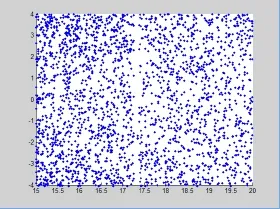
从实验图形中可以看到，我们得到了服从均匀分布的随机数序列。

讨论这个随机数列对初值的敏感性

选取小的ε=0.0000001，初值0.8不变，计算后取出随机数的后十一位来观察对比：（在源程序中最后加入h=t（90：100，2）），将提取的数字做出如下表格。

X=0.8 X=0.8000001 -5.8181 0.5527 0.0051 11.4135 0.0773 9.2396 1.1499 2.5869 -9.1646 3.5347 -3.3648 -4.0799 3.0104 -3.6611 1.9049 3.7946 -11.1777 -2.3968 -13.8536 -0.8297 12.2066 0.9833

从表格中可以发现，当初值有很小的变化ε时，得到的两组随机数完全不同，说明这个随机数列对初值有敏感性。

讨论随机数列初值的取值范围

信息化建设过程中，首先要建立信息化的办公平台，通过办公平台，实现数据信息的共享和互通有无，提高信息的使用率和高效性，所以加强基础设施的建设，是信息化建设的基础内容。同时，企业中要建立内部信息系统，为企业的工作人员提供便利的信息服务条件，方便各个部门能够进行信息的互通，提高了工作的效率，同时也节省了许多运行成本，最终提高了企业的管理水平。

从函数的形式上看，这个函数为奇函数，x取值的正负只影响到结果的符号，不会影响函数的收敛性。当初值x取0时，可以得到图形如下，可以看到这个序列的值全为0.当x不为0时，经过大量实验发现，得到的均为随机数序列形式。所以猜测此函数的初值的取值范围是x≠0。

对此函数取初值0.8，a1=1，a2=10，可得到如下图形。

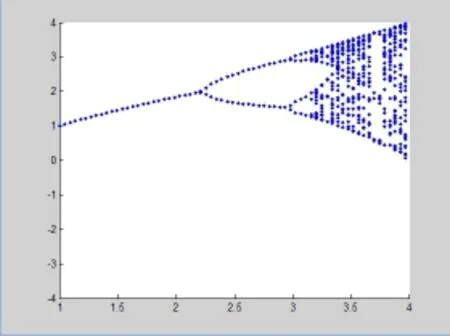
从图中我们可以看出，其混沌行为与logistic函数比较相似，经过试验调整选择a1=3.85，a2=4，x=0.8，y的取值范围为（1，3.5）则有：

取x=0.8000001时后十一位随机数的对比：

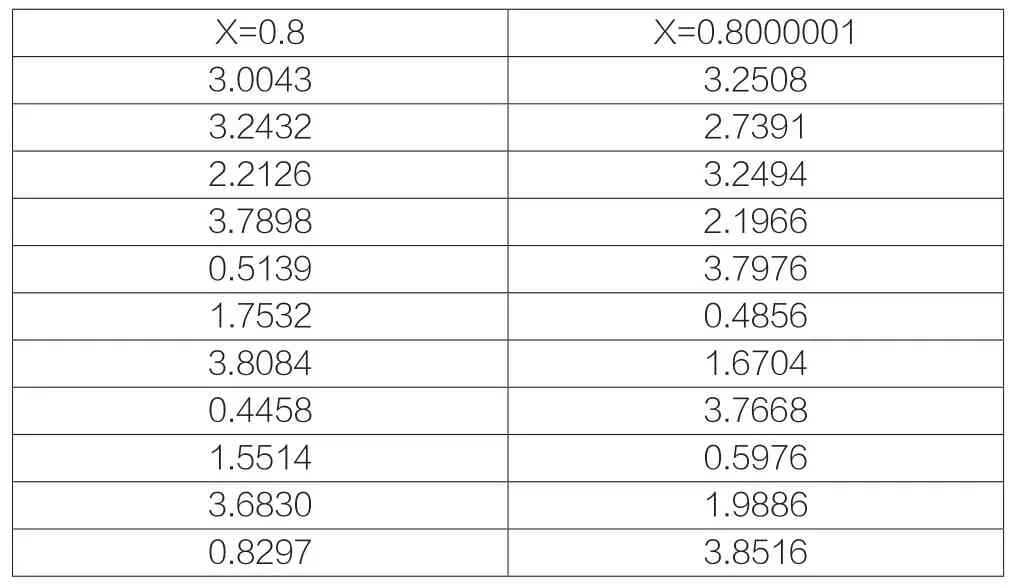
X=0.8 X=0.8000001 3.0043 3.2508 3.2432 2.7391 2.2126 3.2494 3.7898 2.1966 0.5139 3.7976 1.7532 0.4856 3.8084 1.6704 0.4458 3.7668 1.5514 0.5976 3.6830 1.9886 0.8297 3.8516

可以发现此函数对初值也具有敏感性。

伪随机序列的应用

伪随机序列是具有某种随机特性的确定的序列，它是由随机序列产生器产生的确定的序列，然而它们却是具有某种随机特性的随机序列。其具有良好的随机性并且具有预先的确定性和可重复性。由于伪随机序列的这种特性，它可以作为以下几种应用。

测量通信系统的性能时，经常需要使用噪声产生器，由它给出具有所要求的统计特性和频率特性的噪声，并且可以随意控制其强度，以便得到不同的信噪比条件下的系统性能。同样在图像处理等领域，可以用随机序列做噪声的仿真实验。

2密码学的应用

可以用这个函数列作为密码的密钥。即可以用其产生的随机数当做密码，由于其对初值具有敏感性，在被截获时不容易被破译。只要发送和接受密码的人同时知道函数列就可以完成加密和解密。

3通讯中的应用

伪随机序列的这些特性使得它在伪码测距、导航、遥控遥测、扩频通信、多址通信、分离多径、数据加扰、信号同步等方面得到了广泛的应用。

白金鑫1宋运娜2

1.齐齐哈尔医学院基础医学院；2.齐齐哈尔医学院 高数教研室

白金鑫（1991.11-）女，本科，学生。通讯作者：宋运娜（1978.05-），女，硕士，讲师。

10.3969/j.issn.1001-8972.2015.16.003

齐齐哈尔医学院大学生课外科研课题 黑龙江省大学生创新创业训练计划面上项目 齐齐哈尔医学院教育科研项目（JY20141008）