悬窗滑撑受力分析
经验人:黄 锋
悬窗滑撑受力分析
经验人:黄 锋
悬窗滑撑在窗扇重力作用下,受力主要集中在各连杆的支点上,本文从静力学角度,运用合力矩定理和平面力系的平衡方程,对悬窗滑撑各支点进行分析,计算出各支点的反力及滑块受到的摩擦力。
现实生活中有悬窗掉落事情发生,对悬窗滑撑关键受力点进行力学分析非常有必要,本文从静力学角度,分析悬窗滑撑在窗扇重力作用下各杆件连接支点的受力情况,并推导出反力的计算方法和滑码摩擦力的计算方法,希望对业内悬窗滑撑的分析和设计有帮助。
力学模型的建立及分析
假设条件
假设悬窗滑撑的连杆为刚体,在任何状态下不发生弹性变形;铆钉抽象为支点,悬窗滑撑内部零件相互摩擦力忽略不计;悬窗滑撑连杆自重忽略不计;滑码对支点的力矩忽略不计。悬窗滑撑的组成和名称如图1。
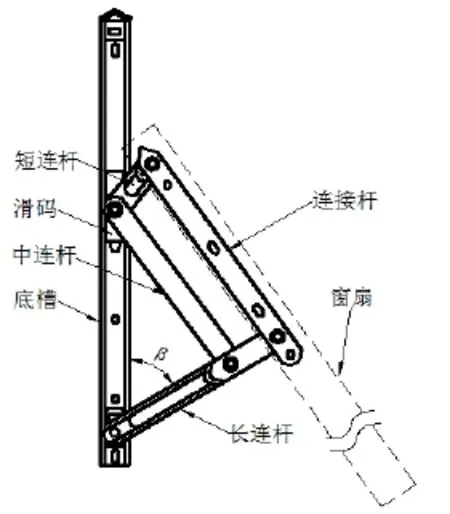
图1 悬窗滑撑的组成示意图
力学模型
由图1可以得出悬窗滑撑的力学模型,各杆件支点的命名如图2。
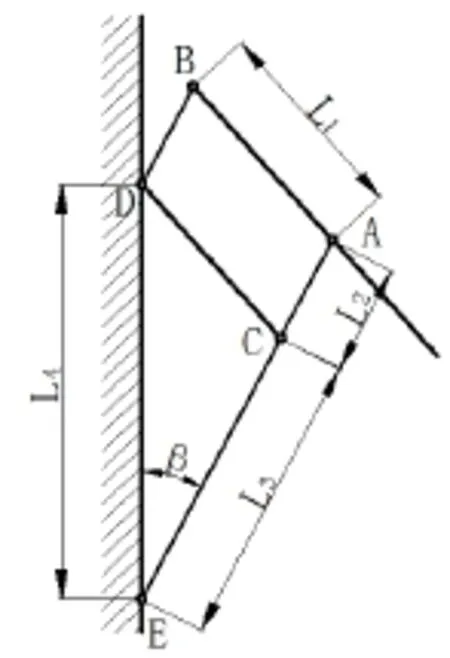
图2 悬窗滑撑的力学模型
由图2可知,各连杆的长度都为已知量,角度β已知,在此状态下的各连杆的相对角度关系均可由正弦定理及余弦定理求得,具体求解过程从略。以静力学为基础对整个悬窗滑撑只受重力作用时,受力分析如下。
连接杆AB为研究对象
作用在连接杆AB上的力有窗扇的重力G,由于悬窗滑撑是配对使用,所以每个悬窗滑撑承受的力为窗重为在A点所受的铰链反力在B点受的铰链反力FB,由于连杆BD为二力杆,在两端所受的力通过均通过连杆BD的轴线,L0为B点到窗扇重心投影在杆AB的距离。连接杆AB的受力如图3所示,其中图示的所有角度大小均可由三角函数求得,具体计算步骤此处从略。
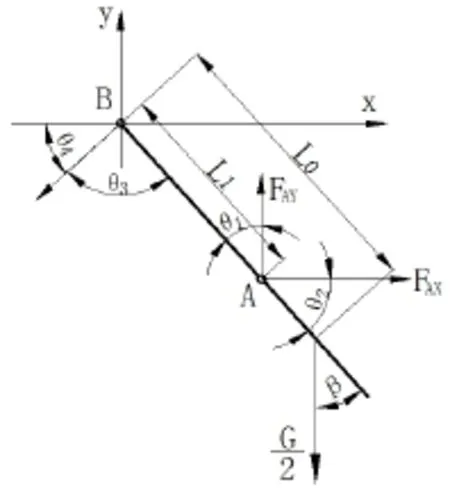
图3 连接杆AB的力学模型示意图
得
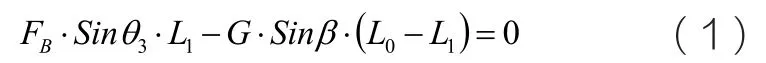
根据平面力系的平衡方程

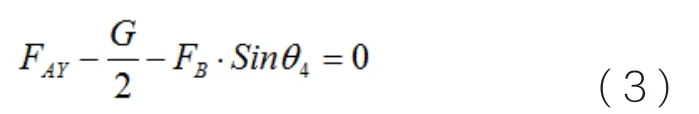
由公式(1)(2)(3)可得:
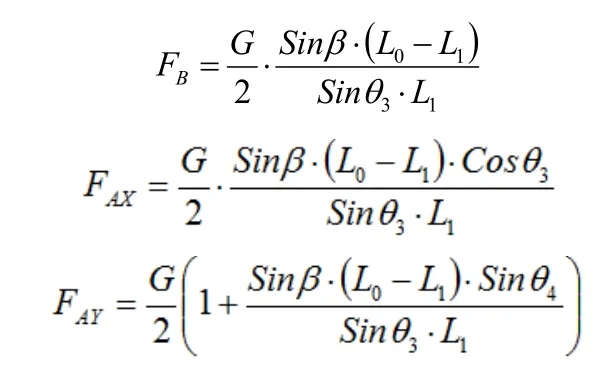
长连杆ACE为研究对象
作用在此连杆上的力有A、C、E三点的反力。由于CD杆为二力杆,在C点的受力通过中连杆CD的轴线,其中对长连杆ACE的受力分析如图4所示,图中所标角度可通过三角函数求得,具体计算步骤从略。
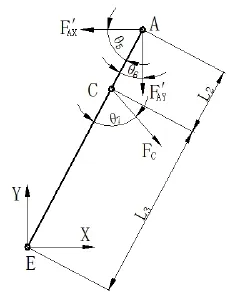
图4 长接杆ACE的力学模型示意图
E点受到的合力矩为零:
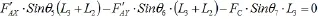
可得:
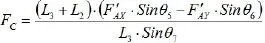
分别取中连杆CD和短连杆BD为研究对象
两连杆在支点的受力都在连杆的轴心方向,力学模型如图5所示。
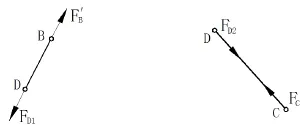
图5 短连杆BD和中连杆CD的力学模型示意图
可得:
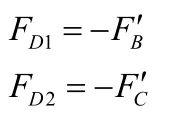
取滑码D为研究对象
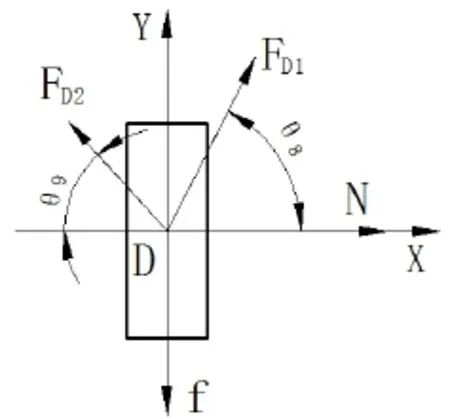
图6 滑码的受力分析示意图
根据力的平衡方程得:
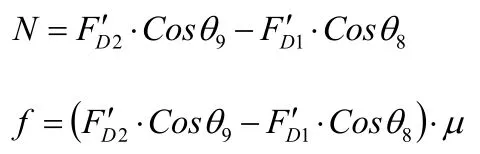
此时,在Y轴方向除f以外所有力的合力F为:
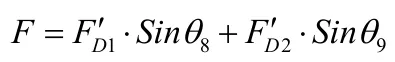
若F≤f ,则滑撑保持静止;若F>f,滑撑将向符合窗扇关闭的方向运动,一直运动到符合条件F≤f时,滑撑保持静止。
实际应用
在实际悬窗滑撑的计算中,窗扇通常受到风压、承重等多力作用的情况,本文各连杆支点反力的计算方法同样适用于上述情况,先计算窗扇受的合力,再计算各支点的反力,推到出铆钉承受的应力强度,与铆钉材料的屈服强度进行校核;
支点反力的计算方法,可以运用于产品研发阶段的设计计算,因支点反力等于铆钉受到的剪切力,应用材料的许用的屈服强度值计算出铆钉直径尺寸,保证铆钉设计的可靠性,提高设计效率。
本文摩擦力的计算,为悬窗滑撑符合行业标准启闭力(摩擦力≤40N)要求,提供了方法。
结语
据报道,在风作用下,悬窗掉下砸人事件时有发生,给人们造成很大的损失;产生悬窗掉下的原因有很多,因为窗扇只固定在悬窗滑撑的连接杆上,所以产品设计时我们应该充分考虑各支点铆钉的受力,考虑克服启闭力的技术壁垒;希望本文的计算方法对业内人员有帮助。

黄 锋
广东合和建筑五金制品有限公司
黄锋(1979),男,本科学历,从事建筑门窗五金产品的设计和技术管理工作。
10.3969/j.issn.1001-8972.2015.16.056

