气流流路对高压SF6断路器介质强度混沌影响

冷 雪 刘晓明 曹云东 韩 颖 王尔智

（沈阳工业大学电气工程学院 沈阳 110870）

1 引言

高压 SF6断路器以其良好的灭弧能力被广泛应用于高压、特高压及超高压输电线路中。当系统出现短路时，高压 SF6断路器能否快速切断故障，主要决定于短路电流过零后弧隙是否发生重燃。而弧隙重燃与否主要取决于灭弧室内零后介质强度的恢复特性[1]。高压 SF6断路器容性小电流下的介质恢复是研究短路大电流开断的基础，其取决于机构运动特性、灭弧室内电场及各气流参数的场空间分布。而 SF6断路器灭弧室内部喷口结构是开断过程中吹弧气体流动行为的主要影响因素，对气流参数起着调控作用，直接影响开断过程中断口区域内介质强度的恢复。灭弧室内喷口结构的设计是 SF6断路器整机设计中的核心内容之一[2,3]。

国内外学者对断路器喷口结构设计与性能分析开展进行了诸多研究，如以压气式断路器和自能式断路器为研究对象采用不同喷口材料进行的实验研究发现喷口材料影响 SF6断路器的开断特性，电弧烧蚀使喷口烧蚀，且喷口材料与 SF6气体相互作用[4]。改变喷口喉部直径、上下游区型面尺寸和喷口下游区尺寸后发现喷口各区域尺寸结构参数对开断性能和喷口烧蚀均有影响[5]。开断电弧过程中若存在电击穿，会影响热开断性能及气体吹弧性能和电气特性[6]。喷口烧蚀[7-9]粒子与SF6等离子体混合影响吹弧性能。

喷口结构使气体流路复杂多变、非线性明显，前期研究[10,11]发现，开断过程中气流在不可压缩、有黏介质、变边界流路中的跨音速流动存在混沌现象。为找到影响混沌的主要因素，有效控制混沌，本文采用有限元法与有限体积方法分别对不同喷口结构灭弧室内部电场与冷态气流场进行数值模拟，得到电场强度与气流参数的场空间分布。并在此基础上，采用混沌时间序列方法[12-16]分析其混沌特性，描述介质强度的混沌效应。

2 多物理场数学模型

2.1 湍动气流场数学模型

断路器开断过程中，气流运动满足流体力学运动条件，采用有限体积法对550kV单断口高压SF6断路器冷态气流场进行数值模拟。仿真过程中，将灭弧室气流场视为二维轴对称场。假设气流运动满足局部热力学平衡（LTE）条件，基于 N-S控制方程，同时引入标准k-ε二方程进行气流场数值模拟，控制方程组如下：

质量守恒方程为

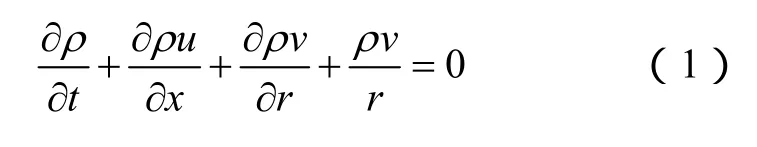
轴向动量守恒方程为

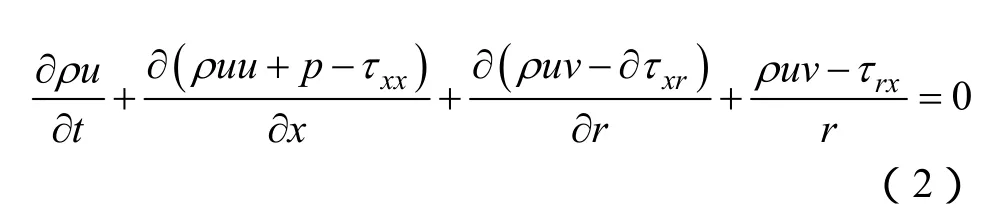
径向动量守恒方程为

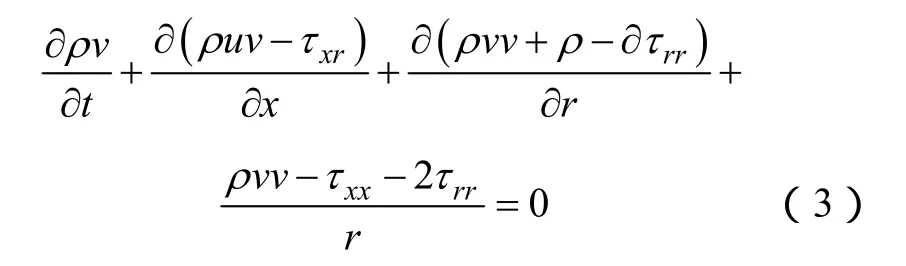
能量守恒方程为

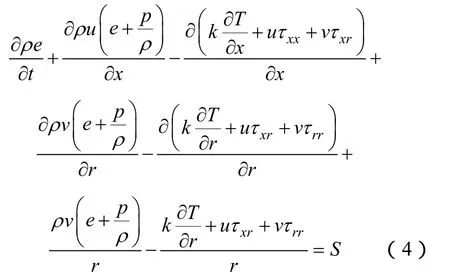
气体状态方程为

粘性应力张量各分量为

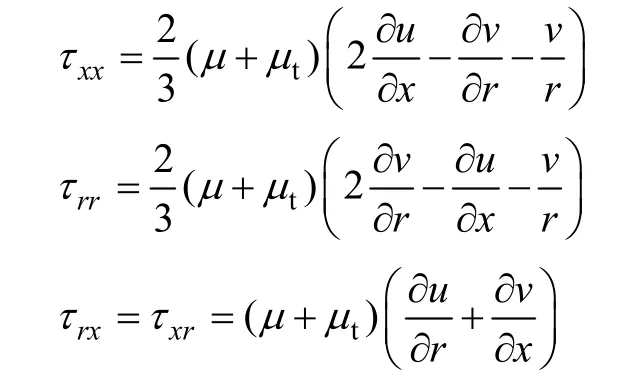
标准k-ε二方程能较好反映断路器气流湍动特性，其描述如下：

湍动能k方程为

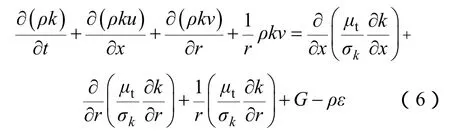
湍流耗散率ε方程为

式中k——湍动能；

σε—— 湍流耗散率普朗克常数；

σk—— 湍动能普朗特常数；

ε—— 湍流耗散率；

G—— 湍动能k的产生项。

基本常数Cμ=0.09；C1=1.43；C2=1.92；σk=1.0；σε=1.3。μt为湍流粘性，且

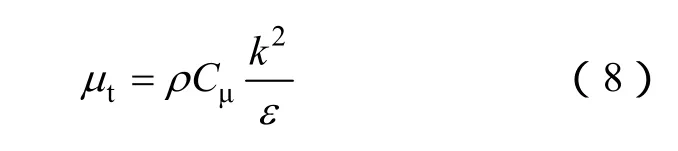
2.2 电场数学模型

采用有限元法对灭弧室内电场进行数值分析，其拉普拉斯方程边值问题描述如下：

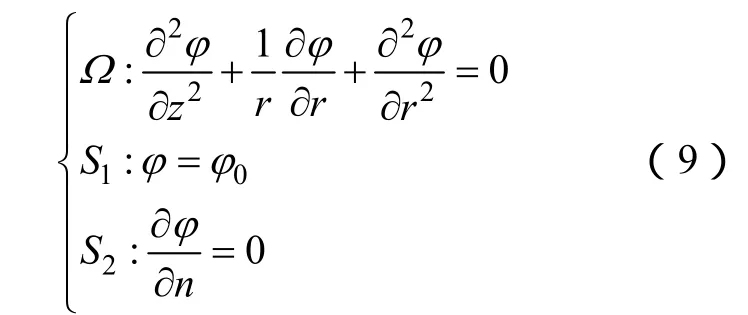
式中Ω——求解域；

φ—— 待求解电位；

φ0—— 已知电位值（动弧触、动主触及其金属连接件为地电位；静弧触、静主触及其金属连接件为高电位）；

z，r—— 轴向与纵向坐标；

S1，S2—— 求解域的狄里克莱（Dirichlet）条件和诺依曼（Neumann）条件。

2.3 不同喷口结构型面物理模型

喷口结构是有效控制气流流路的核心部件，其型面与长度直接影响气流流动及介质强度的恢复。灭弧室计算结构示意图如图1a所示；对于无缩放喷口结构，喷口长度xi=1 78 + 2 0i（i=0,1,2,3），如图1b所示；型面改变以三级缩放结构为例，如图 1c所示。（七种喷口结构：Ⅰ型是长度为 178mm的无缩放型面喷口结构，Ⅱ型是长度为198mm的无缩放型面喷口结构，Ⅲ型是长度为 218mm的无缩放型面喷口结构，Ⅳ型是长度为 238mm的无缩放型面喷口结构；Ⅴ型是长度为218mm的一级缩放型面喷口结构；Ⅵ型是长度为 218mm的二级缩放型面喷口结构；Ⅶ型是长度为 218mm的三级缩放型面喷口结构）。在气流流路典型位置处设置 6个混沌特征量采样点（分布见图2），分别对压力、马赫数及温度等气流参数进行混沌特性分析。

图1 灭弧室及喷口结构示意图注：区域 A为无缩放结构的介质强度薄弱点区域；区域 B为有缩放结构的介质强度薄弱点区域Fig.1 Structure of arc quenching chamber and nozzle

图2 气流参数采样点所在位置示意图Fig.2 Sampling points of the gas flow parameters

3 气流参数混沌特性分析

气流场数值模拟条件：

（1）灭弧室内充气压力0.6MPa（是指环境温度为20℃时的压力值，为相对压力）；行程260mm，超程70mm，分断时间45ms。

（2）边界条件设置：压气缸入口为压力入口边界，入口压力随机构压力-行程变化而变化，出口压力设为0.6MPa，其余边界为固壁。

数值求解得到不同喷口结构下气流参数的场空间分布，在此基础上，利用对照分析手段对比分析了七组喷口结构在不同行程下场参数分布。其中，三级缩放喷口结构（Ⅶ型）80%开距下气流参数分布如图3所示。

图3 80%开距下气流参数分布Fig.3 Distribution of gas flow parameters under 80%opening stroke

对各行程下气流参数数据采样分析，得到不同喷口结构下气流参数时间序列，采用C-C方法（关联积分方法）和LE指数方法（最大Lyapunov指数计算方法）计算气流参数时间序列。C-C方法是用来求取延迟时间和嵌入维数，通过相空间重构将一维时间序列中蕴藏的规律在高维重构后显现出来，通过 Wolf算法[17]计算后，得到不同喷口结构和型面下的混沌特征量分布。不同喷口结构下灭弧室内气流参数采样点数据，若系统最大 Lyapunov指数（LEmax）为正值，说明系统存在混沌现象[18]，经 Wolf算法混沌分析，所得LEmax为正值，说明断路器开断过程中存在混沌现象。为对比分析不同喷口结构下的混沌特性，得到其混沌特征量对比图，如图4所示。

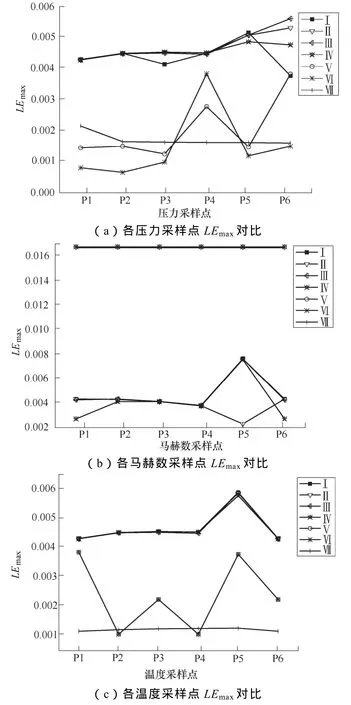
图4 不同喷口结构各采样点LEmax对比Fig.4LEmaxof the sampling points for different nozzle structures

由图4得出：对于压力和温度参数采样点，有缩放结构的LEmax值明显小于无缩放结构，而马赫数则是有缩放结构的LEmax值明显大于无缩放结构；说明增加缩放结构后气流运动剧烈程度增强。由图4a可以看出位于喷口喉部的P4压力采样点的LEmax较其他采样点的波动性较大，这是由于在喷口喉部位置有一个小的“缩放”结构的凹槽，使得气流在流经喷口喉部时出现了跨音速流动，并且伴随有激波和湍流等现象，气体流动表现出强烈的不稳定性。由于喷口结构为典型的拉伐尔喷口，可产生超音速气流，通过对喷口设置“缩放”的结构来减缓气流的流速（包括喷口上游），从而提高喷口内的气体密度。喷口“缩放”结构对流路起限制作用，但并不意味着在开断的各行程下灭弧室全部节点上的气流流速减缓，密度增高；且由于气流在喷口内的堵塞作用会造成喷口上游的气体压力增加，因此会对压气室及上游P1-P3采样点的混沌特性有所影响。无缩放的四种结构（Ⅰ型-Ⅳ型）压力采样点的LEmax变化并无太大差异，而有缩放结构的（Ⅴ型-Ⅶ型）由于其喷口型面的改变会导致在气流流动过程中气流呈现复杂多变的特点，因此其对应压力采样点的LEmax起伏变化也比较大。图4b的马赫数采样点变化说明了有缩放结构（Ⅴ型-Ⅶ型）中气流流速的混沌特性要明显强于无缩放结构（Ⅰ型-Ⅳ型），在喷口下游的 P5、P6采样点的变化波动是由于喷口长度不同导致整个开断过程中，喷口通道完全打开的位置不同，使得气流堵塞的时间不同，造成了流经喷口下游气流运动的差异。图 4c的温度采样点为冷态气流运动下无电弧产生，因此温度混沌特性对于介质恢复强度影响较小。

在开断过程中，混沌特性越弱表明压力参数非线性程度越小，且变化趋势与机构的压力行程特性相一致，对开断过程越有利；冷态气流下，无电弧产生，温度混沌特性影响小；介质恢复特性是衡量断路器开断能力的性能指标，为进一步描述混沌特性的影响，求得不同喷口结构介质强度恢复特性，以找寻混沌特性与介质强度恢复之间的关系。

4 介质强度及混沌特性分析

介质强度的恢复是一个非常复杂的过程，它涉及了断路器开断过程中灭弧室气流场参数分布和变化、灭弧室动静触头间电场的分布和断口间温度场的分布变化，对其求解过程是一个多物理场耦合的数值求解过程。流注理论可较好地解释高气压大间隙非均匀电场导电通道的形成过程，本文在介质恢复特性研究中，采用流注理论临界击穿判据求得介质恢复特性。对于均匀电场，在冷态气体击穿情况下，如果电场强度与气体分子密度之比E/N超过一给定值(E/N)*将出现击穿。

作为气体分子密度函数的击穿电压Ub表示为

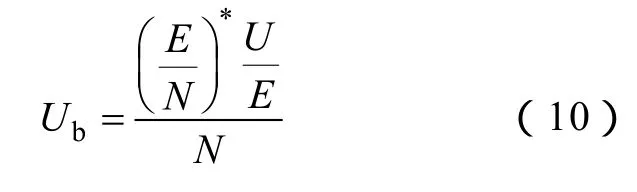
式中E——计算点的电场强度；

U——恢复电压；

N——粒子密度，如下所示

式中，参考粒子密度N0=2 .45× 1 019c m-3，p为计算点压力与p0的无量纲压力比，T0=300K，参考压力p0=1 05Pa ，T为计算点温度，则Ub为

气流场计算中，整个弧隙介质恢复强度取最薄弱点的计算值，得到不同喷口结构下的介质恢复特性曲线如图5所示。

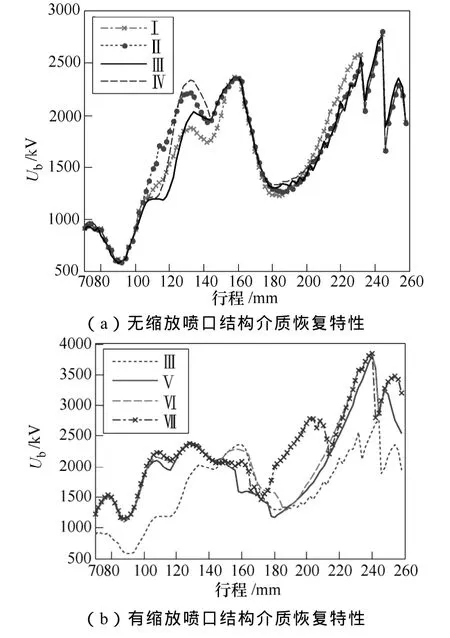
图5 不同喷口结构介质恢复特性Fig.5 Dielectric recovery characteristics fordifferent nozzle structures

分析图5得出：七组喷口结构中，有缩放结构介质恢复特性明显高于无缩放结构；而有缩放结构中，保持喷口长度不变，三级缩放结构优于二级缩放结构，二级缩放优于一级缩放结构；在无缩放喷口结构中，Ⅳ型优于Ⅱ型，而Ⅲ型优于Ⅰ型。其中，Ⅰ型、Ⅱ型、Ⅲ型和Ⅳ型结构的介质强度度最薄弱点位于区域A，Ⅴ型、Ⅵ型和Ⅶ型结构的介质强度度最薄弱点位于区域B，如图1中的b和c所示的区域A和区域B，说明喷口结构改变直接影响到介质恢复特性最薄弱点位置的转移。由图5可以看出，七种不同结构的介质恢复强度薄弱点均出现在行程88～92mm之间，而有缩放结构（Ⅴ型、Ⅵ型和Ⅶ型）的介质恢复强度最小值约为无缩放结构（Ⅰ型、Ⅱ型、Ⅲ型和Ⅳ型）的2倍，缩放结构直接影响断路器介质恢复特性。最薄弱点的转移轨迹，说明喷口结构改变对气流运动的控制，特别是在喷口喉部和“缩放”区域，使气流速度有增有减，以保证良好的介质恢复。

不同喷口结构混沌特性分析：通过对所求击穿电压的相空间重构，得到重构后相空间嵌入维数及延迟时间，采用Wolf算法得到LEmax值见下表。

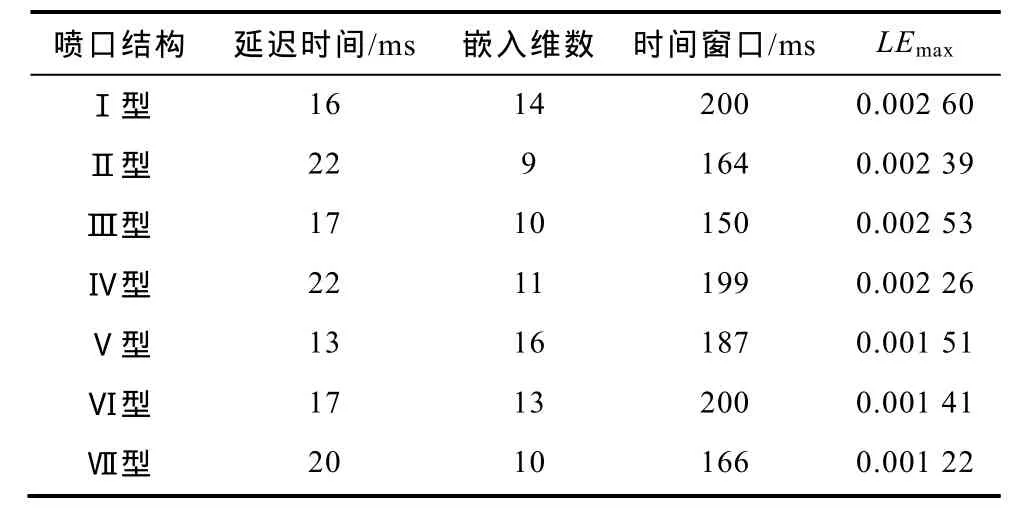
表 不同喷口结构介质恢复特性参数的延迟时间、嵌入维数、时间窗口及LEmaxTab. Delay time, embedding dimension, time window andLEmaxof dielectric recovery characteristics for different nozzle structures

分析表1得出：七组不同喷口长度和型面结构中，有缩放喷口结构的介质特性LEmax小，无缩放结构的介质特性LEmax相对较大；介质恢复特性强的LEmax小，介质恢复特性弱的LEmax大。

研究表明：混沌产生源于气流运动，压气室中气流运动使触头分离过程中产生湍流与激波等现象，由于气流受到流路中喷口及触头等结构型面的限制，使得气流在流路中的运动并非单纯的层流，而出现湍流。湍流本身是耗散系统，因流体流动过程中，为克服内摩擦力，不断将机械能转变为热能而散失，造成流体能量损失，因此湍流粘性是造成气流流量损失的根本原因。开断容性小电流时，气流湍动且在没有电弧作用下的开断过程中存在混沌特性。相比于无缩放结构，有缩放结构速度参数LEmax大，有效利用气流运动特性来提高气流利用率，有利于介质恢复。

5 结论

断路器开断过程中，气流运动存在混沌；改变对喷口结构可改变气流流路，调控气流运动行为，以抑制介质恢复特性的混沌干扰项。不同喷口结构下气流参数混沌特征量分析表明：

（1）各采样点气流参数混沌特性分析表明：相比于无缩放结构，有缩放结构压力、密度和温度参数的LEmax较小，而马赫数相对较大。

（2）击穿电压混沌特性分析表明：开断过程中存在湍流，气流并非层流运动，有效提高气流利用率，有利于开断；对比不同喷口结构下压力参数混沌特性，三级缩放结构介质恢复特性混沌特性最低。

（3）可通过对喷口结构型面参数的调节，改变气流流路，增强气流利用率，减小开断过程中混沌影响以提高介质恢复能力。

[1] 王尔智. 高压 SF6断路器介质恢复特性的数值模拟[M]. 北京: 科学出版社, 2012.

[2] 关盛楠, 王尔智, 刘海峰, 等. 喷口型面及尺寸对SF6高压断路器介质强度恢复特性的影响[J]. 中国电机工程学报, 2008, 28(3): 6-11.

Guan Shengnan, Wang Erzhi, Liu Haifeng, et al.Turbulent flow and its influence on dielectric recovery property in arc nozzle of SF6high voltage circuit breaker[J]. Proceedings of CSEE, 2007, 27(36): 31-35.

[3] 王尔智, 刘晓明, 曹云东. 考虑湍流影响的高压 SF6断路器喷口优化设计[J]. 电工技术学报, 2009, 24(6):30-34.

Wang Erzhi, Liu Xiaoming, Cao Yundong. Optimization design for arc nozzle of High voltage SF6circuit breaker considering turbulent influence[J]. Transactions of China Electrotechnical Society, 2009, 24(6): 30-34.

[4] Meier R, Kneubuhl F K, Coccioni R, et al. Investigations of nozzle materials in SF6circuit breakers[J].IEEE Transactions on Plasma Science, 1986, 14(4):390-394.

[5] 贾继钧, 赵长征, 朱鸣海. SF6断路器喷口形状尺寸对烧蚀的影响及喷口设计方法探讨[J]. 高压电器,1991, 27(4): 28-32.

Jia Jijun, Zhao Changzheng, Zhu Minghai. The nozzle shape and structure effect on the ablation in SF6circuit breaker and the design method of nozzle structure[J]. High Voltage Apparatus, 1991, 27(4):28-32.

[6] Wang Weizong, Yan Jiudun, Rong Mingzhe, et al.Investigation of SF6arc characteristics under shock condition in a supersonic nozzle with hollow contact[J]. IEEE Transactions on Plasma Science, 2013, 41(4):915-928.

[7] Osawa N, Yoshioka Y. Analysis of nozzle ablation characteristics of gas circuit breaker[J]. IEEE Transactions on Power Delivery, 2010, 25(2): 755-761.

[8] Christen Thomas. Radiation and nozzle-ablation models for CFD simulations of gas circuit breakers[C]. 1st International Conference on Electric Power Equipment-Switching Technology, 2011: 471-474.

[9] Park S H, Kim H K, et al. Evaluation on short line fault breaking performance of SF6gas circuit breaker considering effects of ablated nozzle vapor[J]. IEEE Transactions on Magnetics, 2009, 45(3): 1836-1839.

[10] 刘晓明, 冷雪, 曹云东, 等. 550kV SF6断路器气流与电弧相互作用混沌研究[J]. 电工技术学报, 2012,27(6): 46-52.

Liu Xiaoming, Leng Xue, Cao Yundong, et al. Chaotic characteristic analysis of the interaction between arc and the gas flow of 550kV SF6circuit breaker[J]. Transactions of China Electrotechnical Society, 2012, 27(6):46-52.

[11] 刘晓明, 韩颖, 王尔智, 等. 基于多物理场耦合的高压SF6断路器混沌电弧模型[J]. 电工技术学报, 2013,28(1): 165-172.

Liu Xiaoming, Han Ying, Wang Erzhi, et al. Chaos of arc model for SF6circuit breaker based on coupled multiple-physical field simulation[J]. Transactions of China Electrotechnical Society, 2013, 28(1): 165-172.

[12] 吕金虎, 陆君安, 陈士华. 混沌时间序列分析及其应用[M]. 武汉: 武汉大学出版社, 2002.

[13] 黄润生, 黄浩. 混沌及其应用[M]. 武汉: 武汉大学出版社, 2005.

[14] 吕涛, 唐巍, 所丽. 基于混沌相空间重构理论的风电场短期风速预测[J]. 电力系统保护与控制, 2010,38(21): 113-117.

Lü Tao, Tang Wei, Suo Li. Prediction of short-term wind speed in wind farm based on chaotic phase space reconstruction theory[J]. Power System Protection and Control, 2010, 38(21): 113-117.

[15] 陈敏, 李泽军, 黎昂. 基于混沌理论的城市用电量预测研究[J]. 电力系统保护与控制, 2009, 37(16):41-45.

Chen Min, Li Zejun, Li Ang. Forecast research of urban electricity consumption based on chaos theory[J].Power System Protection and Control, 2009, 37(16):41-45.

[16] 修春波, 刘新婷, 张欣, 等. 基于混沌特性分析的风速序列混合预测方法[J]. 电力系统保护与控制,2013, 41(1): 14-20.

Xiu Chunbo, Liu Xinting, Zhang Xin, et al. Hybrid prediction method of wind speed based on chaotic characteristic[J]. Power System Protection and Control,2013, 41(1): 14-20.

[17] Alan Wolf, Jack B Swift, Harry L Swinney, et al.Determining Lyapunov exponents from a time series[J].Physica D: Nonlinear Phenomena, 1985, 16(3): 285-317.[18] John A. An exploration of chaos[M]. Amsterdam: North-Holland, 1994.