一种基于耦合电感的模块化多电平变流器控制

袁义生 朱本玉

（华东交通大学电气学院 南昌 330013）

1 引言

作为新一代直流输电技术，柔性直流输电突破了全控型电力电子器件、电压源换流器和脉宽调制三大技术特点，解决了常规直流输电技术的诸多固有瓶颈[1,2]。传统的直流输电主要基于晶闸管电流源换流器，具有容易发生换向失败、谐波次数低、需要大量无功补偿装置等缺陷，随着电力电子的飞速发展，GTO、IGBT的出现，促使了电压源换流器型直流输电（VSC-HVDC）。目前常见的电压源型多电平变换器拓扑大致可以分为钳位型和单元级联型两大类。前者随着电平数的增加，所需半导体器件的数量急剧增加，且电容电压不容易平衡，使得其在实际应用中有一定的限制[3]。后者对于需要实现有功能量处理的场合，高功率单元需要独立的直流供电电源，极大增加了系统的复杂程度和成本[4,5]。传统的两电平电压源变换器（Voltage Source Converter，VSC）应用于直流输电领域中，存在功率开关器件耐压问题，通常通过工频变压器接入高压电网，笨重的工频变压器大大增加了电力电子变换器装置的体积和成本，并限制了系统效率[6]。模块化多电平变换器直流输电（MMC-HVDC）的产生，成为直流输电技术的一次重大变革。模块化多电平变换器拓扑（Modular Multilevel Converter，MMC）由德国教授Marquard提出，作为一种新型的拓扑结构，具有输出电压谐波含量低、开关损耗小、可拓展性强、易于实现冗余控制等优点，且通过低压子模块的叠加可方便地输出高电压，因此MMC在高压直流输电领域的应用成为近来研究的热点[7]。

近几年研究MMC-HVDC的学者愈加增多，相关文献纷纷涌现，主要集中于对电路数学建模、脉宽调制方案、电容电压平衡、环流抑制、电网不平衡条件运行、低频运行等方面的研究。文献[8-10]提出了MMC新型拓扑结构，文献[8]提出了带中间单元的新型结构，中间单元的加入，使模块选择更灵活，有助于减小电容电压纹波；文献[9]提出了一种双系统桥臂六边形结构，该结构在低频条件下的风力涡轮机中有优越的运行性能；文献[10]提出了一种限制直流短路电流的新型拓扑，该结构有利于正常运行、瞬态、故障情况下直流侧的控制，但带来变流器器件过多的负担。文献[11,12]对电网不平衡时电路的运行进行了分析，并提出相应的策略使系统能在不平衡的电网条件下也能较好的运行,但均未设计到环流抑制问题。文献[13,14]基于最近电平法，由换流器交、直流侧瞬时功率平衡推导出直流环流电流的计算公式，进而分别求得上、下桥臂子模块电容电压的参考值，呈周期性变化，使得子模块电容电压不均衡度明显降低，但阶梯波调制下输出谐波含量大。文献[15,16]提出的特定谐波消除法，消除了输出电压中主要高次谐波，THD减小，但需要求解超越方程组，且随着电平数增加，计算量增大，不适用于在线计算。文献[17-19]将载波层叠法运用于MMC中，此种方法实现简单，但电压利用率低，同时没有很好的考虑中点电压的控制问题，且各开关频率不一致导致损耗不一，不利于变流器的长期运行。文献[20-22]采用载波移相脉宽调制的子模块电容电压平衡控制策略，输出电流波形畸变小，环流也有较好的抑制效果，但该调制法要求每个子模块需要控制器输出对应的调制波来平衡该模块内的电容电压，这样随着子模块的增加需要的控制器也相应增加，这无疑增加了系统的复杂性。文献[23]提出一种新型全桥 VSC-HVDC变流器拓扑，具备直流侧故障处理能力，但全桥结构增加了IGBT的数量以及相应的器件损耗，随着电平数的增加，成本较高。文献[24]将子模块统一脉宽调制法（SUPWM）成功应用在MMC中，该方法使得每相只需一个载波，相比载波移相脉宽调制，载波数大大减少了，而且也达到了增加输出电压等效开关频率的效果。

本文以桥臂电感耦合的模块化多电平逆变器电路为研究对象，该结构可降低桥臂电感电压，减小环流波动，结合排序法、脉宽统一调制方法，建立该变换器结构的数学模型，搭建了仿真模型验证了该方案的有效性，同时对排序法进行了改进，仿真结果进一步验证了改进后方案的有效性。

2 采用耦合电感的MMC拓扑结构与运行原理

2.1 拓扑结构

图1为三相模块化多电平变换器。三相具有严格的对称性，以A相为例，A相由2N个结构完全一样的子模块、耦合电感（异名端相连）以及桥臂等效电阻Rs串联而成，耦合电感中心抽头经滤波电抗器Lf与 A相负载相连。桥臂耦合电感cn在直流侧短路故障下可以用于限制短路电流上升的速度，由于采用的是异名端相连的耦合结构，流过同向电流时等效电感量互相增加，其抑制短路电流上升的效果比传统MMC中使用独立电感的效果更好。在正常运行时则可以用于抑制环流，同样，抑制效果比传统结构要好。MMC的子模块采用半桥结构，由两个IGBT、两个二极管以及一个直流电容组成。

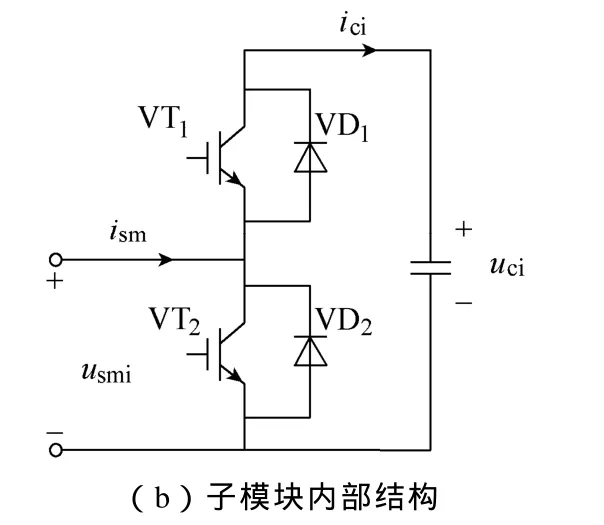
图1 采用耦合电感的三相MMC基本结构和子模块内部结构Fig.1 The basic structures of MMC with coupled inductors and sub-modules

上、下两个开关管不同的开关状态对应于模块不同的输出电压及电容充放电状态见表。通过控制子模块的投入与切除即可叠加出拟合正弦波形的多电平阶梯波。

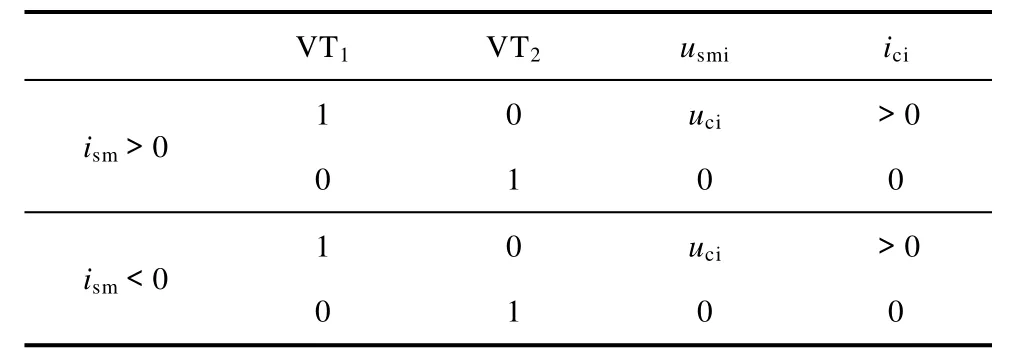
表 电容状态与开关信号的关系Tab. Relationship between capacitor status and signals

2.2 工作原理

各电气量的正方向规定如图 1a所示。假定理想情况下电感为全耦合，互感M=Lp=Ln，以A相为例。

由KCL定律有

式（1）+ 式（2）得

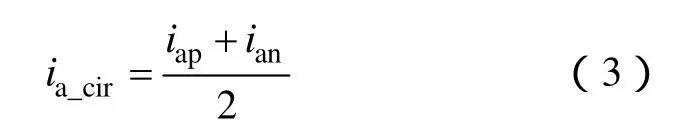
式中，ia_cir为桥臂环流，由直流分量id/3、二次谐波电流以及其他高次谐波电流组成，电路稳定时，环流以前两者为主，不考虑桥臂电流中二次以上的谐波电流，则环流又可表示为

由KVL有

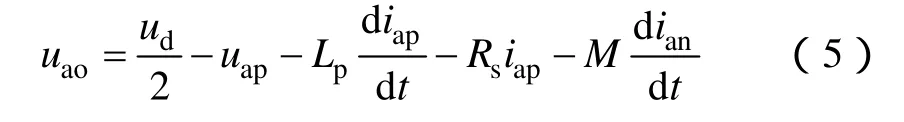
令M=Lp=Ln=L，将式（1）、式（2）代入式（5）、式（6），式（5）+式（6）有

传统MMC结构中

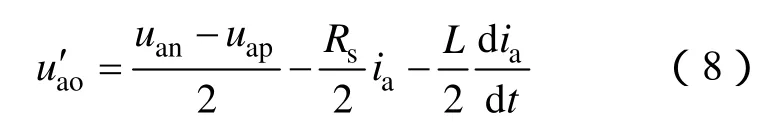
由式（5）、式（6）得

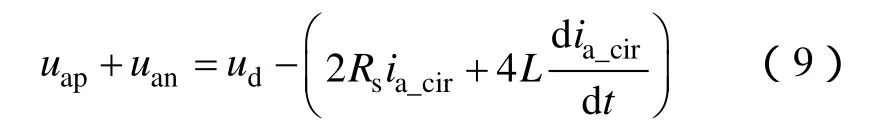
实际电路中桥臂等效电阻Rs很小，Rs<<ω1L为基波角频率，因此相对于(uan-uap)/2，Rsia/2可忽略不计，式（7）与式（8）比较，采用独立电感的传统结构中uao的数学表达式等式右边少了一项-Ldia/(2dt)，这使得输出相电压uao与给定相电压的相位差减小，几乎同相。

对于三相有

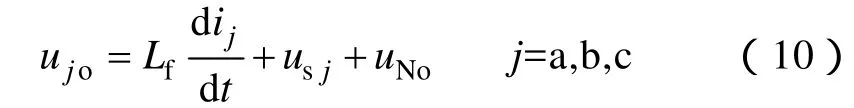
系统稳定工作时，三相对称电流ij和三相电压usj有

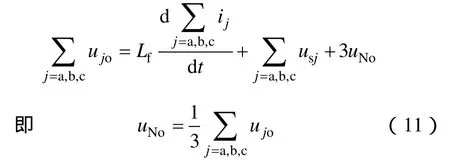
耦合电感的耦合形式有两种：一种同名端相连，一种异名端相连。经过仿真验证，同名端相连的优势在于对于单个桥臂而言，耦合电感上总电压可获得一更小的值，电容电压纹波也因此更小，但在其他方面，如耦合电感分电感上的电压、环流、输出电压电流波形，其效果均差于耦合电感异名端相连的结构。因此，选择耦合电感异名端相连接形式，故上、下桥臂中的基波电流在每个电感上产生相互抵消的电压，分析A相上桥臂电感上的电压如下。

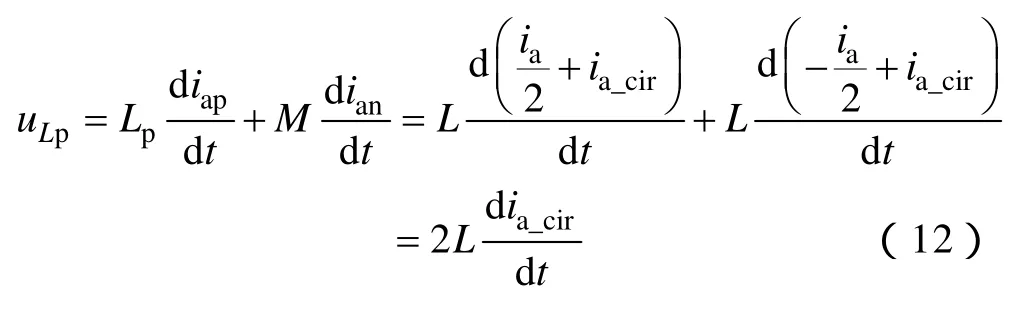
传统MMC结构中

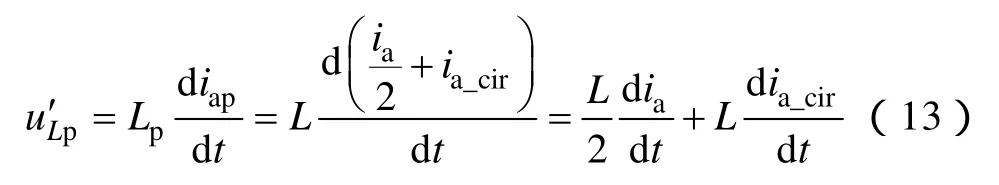
桥臂电流以基波电流为主要成分，环流量相对较少，因此，与传统MMC结构相比，采用耦合电感结构后，电感上的压降大幅度减少了，从而使得单相投入模块电压总和更加趋近直流侧电压，下桥臂电感上的电压与上桥臂相同，控制环流进一步增加换流器的稳态性能。

3 子模块电容均压策略

3.1 调制策略

从式（7）可知，通过控制上、下桥臂电压可得出所需要的输出电压。采用基于子模块电容电压排序的脉宽统一调制法能获得较好的输出电压电流波形。MMC桥臂子模块数一般会达到几十甚至上百个，这样的条件下，输出电压 THD几乎都有较小的值，虽然上、下桥臂载波同相调制法能使输出电压电平数增加几乎一倍的优势，但该调制法会导致桥臂电感上的压降大大增加，进而引起不必要的环流增量，对桥臂电感和开关管提出较高要求。因此，采用上、下桥臂载波反相调制法。对于上、下PWM模块而言，通过给定上、下桥臂参考波形所得到的上、下桥臂PWM调制波反相，为了说明同相与反相PWM调制，PWM模块调制波取正弦波形分析，如图2所示。

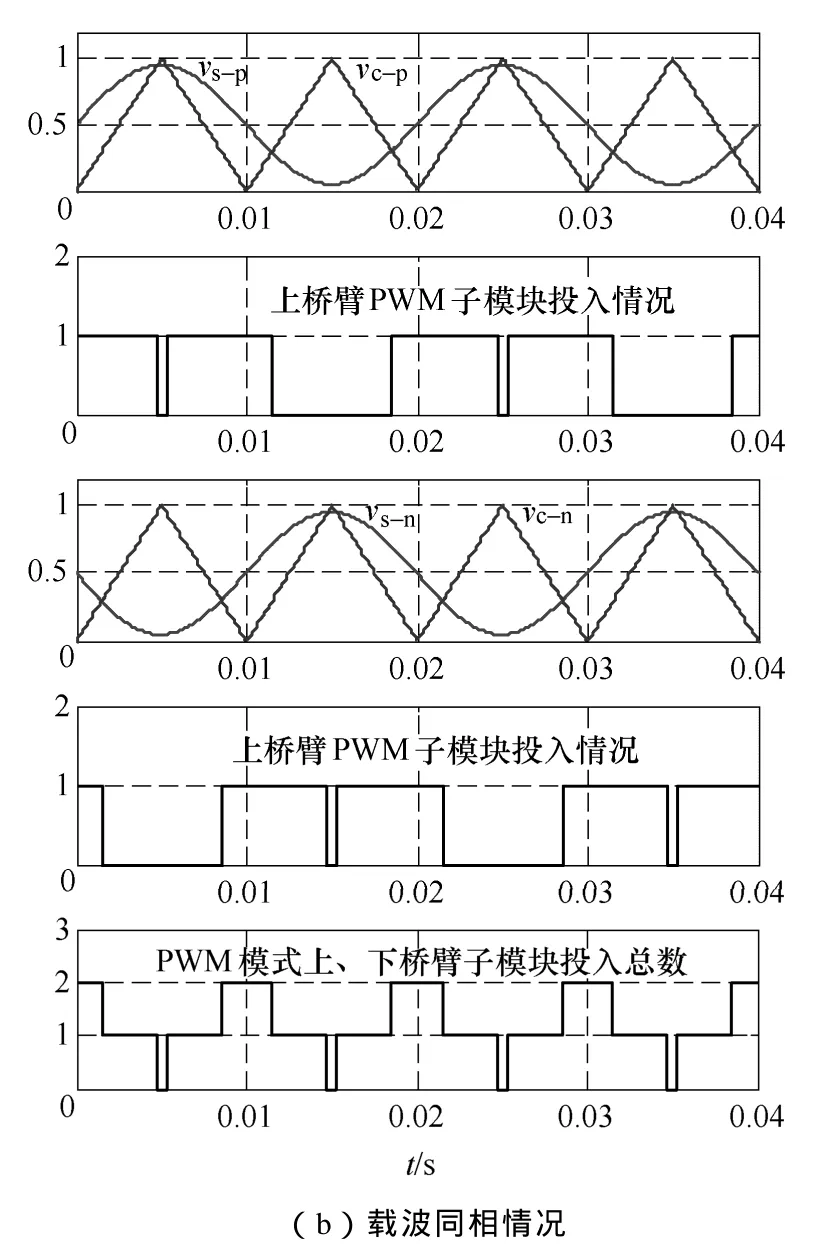
图2 载波反相与载波同相条件下上、下桥臂投入模块数产生图Fig.2 Producing diagrams of the number of inserted-submodules in the bridge, on the conditions of carrier inverting and carrier phase

图2中，vs-n代表下桥臂通过给定电压计算出的PWM模块的调制波，vc-n为下桥臂PWM模块的载波；同样，vs-p代表上桥臂通过给定电压计算出的PWM模块的调制波，vc-p为上桥臂PWM模块的载波，且调制系数取m=0.9。

载波同相条件下，上、下桥臂 PWM输出波形不互补，使得始终 PWM模式的上、下桥臂投入模块总数在 0～2之间变化，即式（21）中na不再为一常数N，而是出现N-1，N，N+1这三个值，这也是造成单桥臂上电感电压较大的根本原因，若忽略Rsia/2，由uao=(uan-uap)/2知，对于uan、uap其中某个量的单一变动必然会引起uao电平增加；反相载波条件下，上、下桥臂 PWM输出波形互补，这使得PWM模式下上、下桥臂子模块投入总数一直为1，因而单相子模块投入总数恒定，如式（21），在电容电压波动小的情况下，有助于环流的减小。

以A相为例，设交流端输出电压为

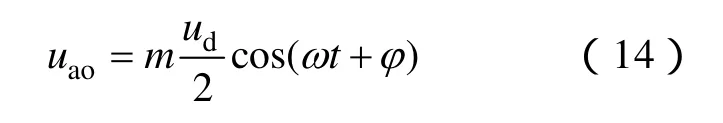
式中m——调制比；

φ——交流电压初相角。

上、下桥臂参考电压为

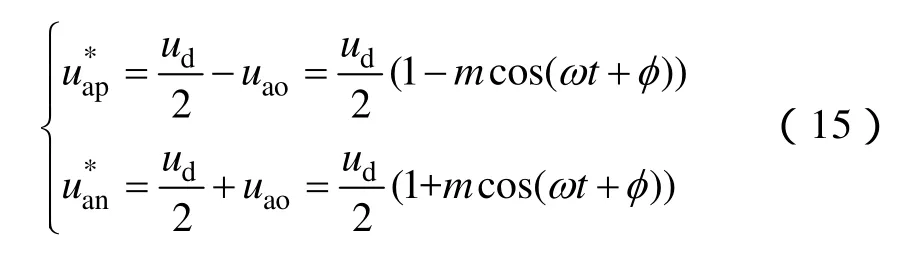
由给定的参考桥臂电压计算桥臂需要投入的子模块数，对于A相上桥臂，子模块数由两部分组成：在整个开关周期内投切状态不变的子模块数ncons和处于PWM状态的子模块数npwm。

式中，floor(x)为对x向下取整。

令

式中，mode(x)为x小数部分；Tc为三角载波。

由以上可知，任意时刻A相上桥臂投入的子模块数为

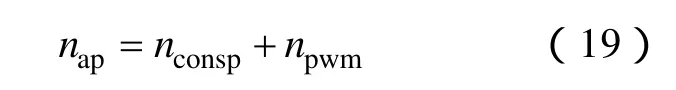
同样可得下桥臂投入的子模块数为

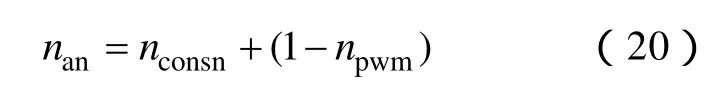
故A相投入子模块总数为

3.2 排序原理及改进策略

对于已计算出的桥臂子模块数，需要对桥臂所有电容电压排序来确定所要投入的子模块。传统的排序法以桥臂电流为参考，以A相上桥臂为例：当桥臂电流iap＞0时，对上桥臂电容电压进行升序排列，选择前nconsp个子模块投入（开关周期内一直处于导通状态），第nconsp+1个子模块处于PWM状态，其余N-nconsp-1个子模块切除，桥臂电流对投入的子模块电容充电；iap＜0时，对上桥臂电容电压进行降序排列，选择前nconsp个子模块投入，第nconsp+1个子模块处于PWM状态，其余N-nconsp-1个子模块切除，桥臂电流对投入的子模块电容放电。下桥臂亦如此。这样的选择投切机制能使子模块电容电压稳定在期望值附近。传统的排序法以iap、ian为参考，实际上，iap、ian上均有一个正的直流分量id/3，这样导致电流大于0的部分比小于0的部分要大，对单个桥臂而言充电时间大于放电时间，如图3所示，传统排序法中，一个周期内t1～t6，t2～t5为上桥臂电容充电时间段，t1～t2以及t5～t6为上桥臂电容放电时间段。充、放电时间不均衡。

图3 A相上桥臂电流iap和输出电流iaFig.3 Upper bridge arm currentsiapand output currentsiain phase A

针对以上问题，对传统排序法进行改进，不选择桥臂电流而选择输出电流ia为参考，同样以A相为例：当ia＞0时，上桥臂子模块电容电压升序排列，选择前nconsp个子模块投入，第nconsp+1个子模块处于PWM状态，与此同时，下桥臂子模块电容电压降序排列，选择前nconsn个子模块投入，第nconsn+1个子模块处于PWM状态，投入的子模块数；ia＜0时，反之。忽略环流，ia与iap变化一致，且ia相对于iap来说少了直流分量，再者，经过滤波电感，输出电流THD较小，接近标准余弦波形，如图3所示，t1～t3以及t4～t6为上桥臂电容放电时间段，t3～t4为上桥臂电容充电时间段，理想情况下(t3-t1)+(t6-t4)=t4-t3，因此能更好的平衡桥臂电容充放电时间，更加有利于电容排序时对子模块的平衡选择，并且使直流端电流能更快稳定，仿真实验验证了这一结论。

4 仿真分析

为验证上述耦合结构的优越性以及改进排序法的有效性，本文利用 Matlab/Simulink软件搭建立了MMC的变流器仿真模型，对传统的三相MMC变流器电路、加入耦合电感的三相MMC变流器电路分别进行了仿真对比分析，仿真均采用统一脉宽 PWM调制法，改进控制方法后，再进行了仿真分析，对比分析了改进前后对直流侧电流的影响。仿真模型中，每相单个桥臂子模块数为N=5，直流侧电压Ud=5 000V，桥臂子模块电容C=11.2mF，桥臂耦合电感L=3mH（理想情况下为全耦合状态），输出滤波电感Lf=3mH，负载呈阻感性质，Lo=3mH，Ro=10Ω，调制系数m=0.9。

从图4可知，两种结构输出电流波形相当，耦合电感结构输出电流波形 THD略微减小。比较图5a、5b波形可知，和传统结构相比，采用耦合电感结构后，环流波动减小了近一半。图6中ucap为上桥臂子模块电容电压，ucan为下桥臂子模块电容电压，由图6a、6b比较知，耦合电感结构中，上、下桥臂子模块电容电压相对比较平衡，因此，电容电压的平衡性更好。图7中波形表明，采用耦合电感结构后，桥臂电感上电压幅值由 300V降低为30V，变化相当大，且桥臂电感上电压的谐波含量大量减少，主要谐波为二次谐波，其他高次谐波含量很少，而传统结构中电感电压高次谐波含量丰富。图8a、8b比较表明耦合电感结构还使得直流侧电流波动有所减小，由25A波动幅值降低为10A。图8b与图9是对排序法进行改进前后所得到的直流侧电流，显然，后者的电流波动较前者小，由前者 10A的波动值减小为 4A。这些无疑更有利于电路的运行，降低了电路设计要求。仿真结果符合理论分析，提出的改进策略降低了直流侧的电流波动。

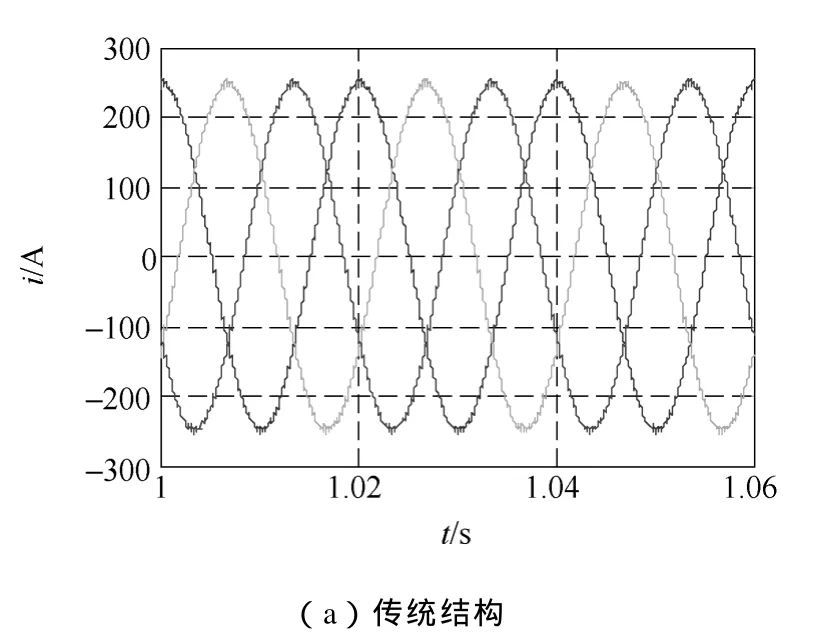
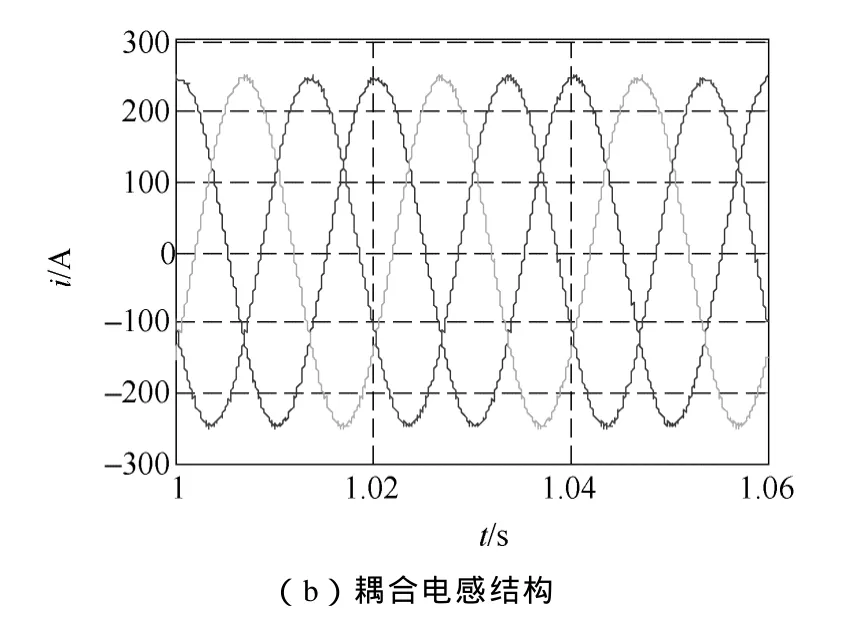
图4 传统结构输出电流与耦合电感结构输出电流Fig.4 Output currents from the traditional MMC converter and the converter with coupled inductors

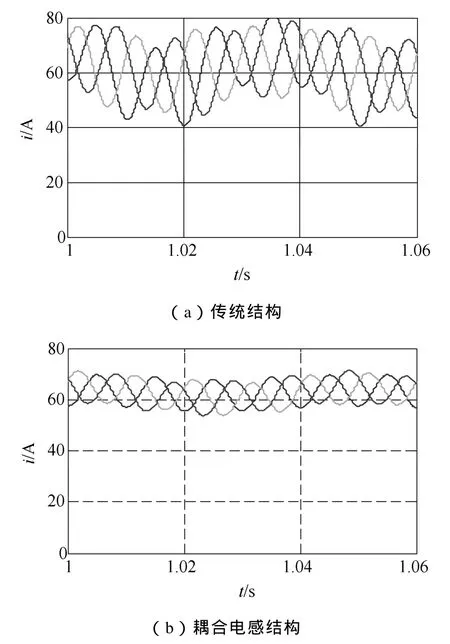
图5 传统结构环流与耦合电感结构环流Fig.5 Circulating currents from the traditional MMC converter and the converter with coupled inductors

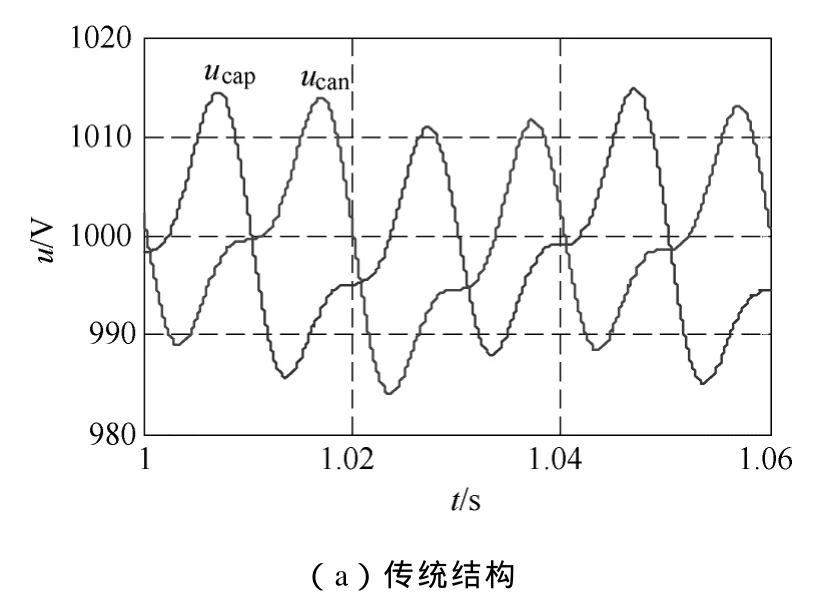
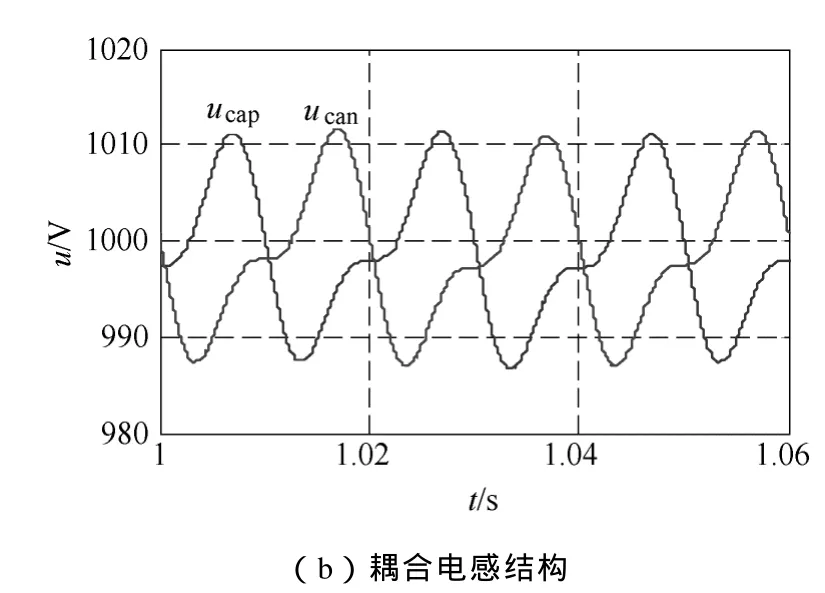
图6 传统结构桥臂电容电压与耦合电感结构桥臂电容电压Fig.6 Voltages of capacitors from the traditional MMC converter and the converter with coupled inductors

图7 传统结构与耦合电感结构桥臂电感电压Fig.7 Voltages on the bridge inductors from the traditional MMC converter and the converter with coupled inductors

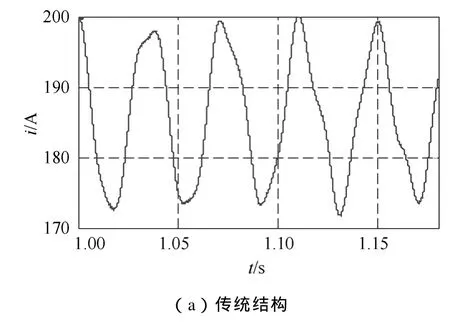
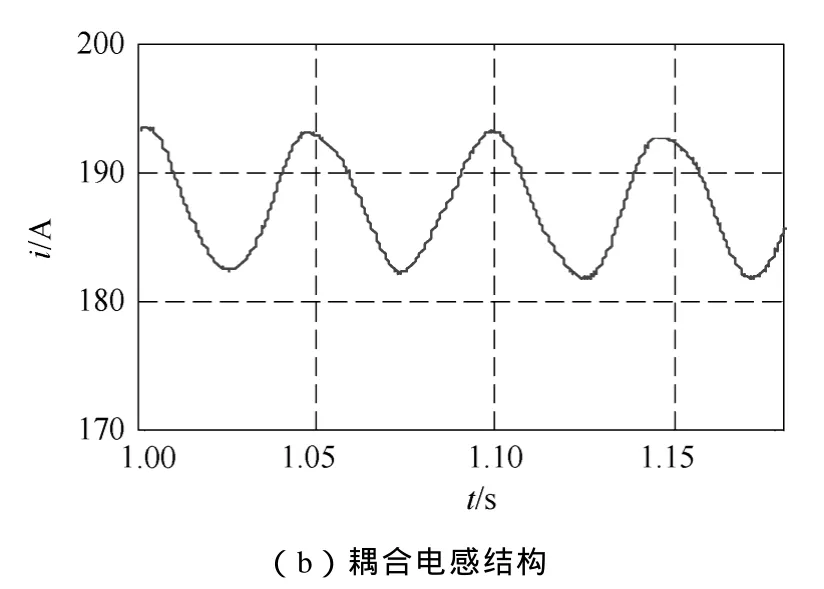
图8 传统结构直流侧电流与耦合电感结构直流侧电流Fig.8 DC currents from the traditional MMC converter and the converter with coupled inductors

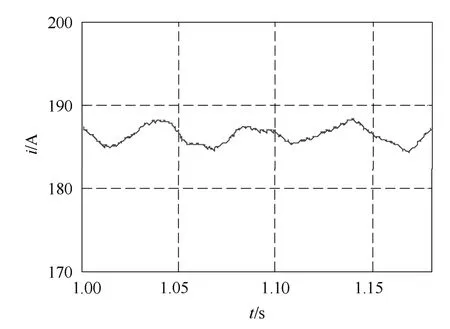
图9 基于耦合电感结构改进排序法后的直流侧电流Fig.9 DC currents from the MMC converter with coupled inductors based on an improved sorting method

5 结论

本文针对模块化多电平变流器进行了深入研究，分析了桥臂采用耦合电感结构的MMC变流器的基本原理，建立了逆变器的数学模型，分析了桥臂电感电压、桥臂环流等量，针对MMC输出电平数高的特点，提出了适用于MMC的PWM方法，在排序法的基础上对同相、反相载波调制做了相关分析，对传统排序法中出现的问题提出了改进策略。为了验证所述电路结构和提出的改进措施的有效性，在Matlab/Simulink环境下搭建了6电平MMCHVDC仿真模型，环流得到进一步抑制，电感电压仿真结果符合理论分析，直流侧电流的波动减小，证明了本文所述结构的有效性以及改进策略的正确性，为MMC—HVDC实际工程提供了理论依据。

[1] 徐政, 陈海荣. 电压源换流器型直流输电技术综述[J]. 高电压技术分析, 2007, 33(1): 1-10.

Xu Zheng, Chen Hairong. Review and applications of VSC HVDC[J]. High Voltage Engineering, 2007,33(1): 1-10.

[2] Dietmar Retzmann, Karl Uecker. Benefits of HVDC& FACTS for sustainability and security of power supply[C]. Power Africa Conference and Exposition,2007: 55-60.

[3] Rodriguez, Lai Jihsheng, Peng F Z. Multilevel inverters:a survey of topologies, controls, and applications[J].IEEE Transactions on Industrial Electronics, 2002,49(4): 724-738.

[4] Wang Kui, Li Yongdong, Zheng Zedong. A new transformerless cascaded multilevel converter topology[C]. IEEE Energy Conversion Congress and Exposition,California, USA, 2009: 3124-3129.

[5] Peng Fangzheng, Lai Jisheng, McKeever J W, et al. A multilevel voltage-source inverter with seperate DC sources for static var generation[J]. IEEE Transactions on Industry Applications, 1996, 32(5): 1130-1138.

[6] Ichikawa F, Suzuki K, Nakajima T, et al. Development of self-commutated SVC for power system[C].Record of the IEEE Power Conversion Conference,Yokohama, 1993: 609-614.

[7] 刘隽, 贺之渊, 何维国, 等. 基于模块化多电平变流器的柔性直流输电技术[J]. 电力与能源, 2011,1(1) : 33-38.

Liu Jun, He Zhiyuan, He Weiguo, et al. The introduction of technology of HVDC based on modular multi-level converter[J]. Power & Energy, 2011, 1(1): 33-38.

[8] Wang K, Li Y, Zheng Z, et al. Voltage fluctuation suppression method of floating capacitors in a new modular multilevel converter[C]. Conf. Rec. of IEEE ECCE, 2011: 2072 -2078.

[9] Baruschka L, Mertens A. A new 3-phase direct modular multilevel converter[C]. Proc. 14th Eur. Conf. Power Electron. Appl, 2011: 1-10.

[10] Marquardt R. Modular multilevel converter topologies with DC-Short circuit current limitation[C]. IEEE 8th International Conference on Power Electronics and ECCE Asia-ICPE ECCE , 2011: 1425 -1431.

[11] Guan M, Xu Z. Modeling and control of a modular multilevel converter-based HVDC system under unbalanced grid conditions[J]. IEEE Transactions on Power Electronics, 2012, 27(12): 4858-4867.

[12] Song H S, Nam K. Dual current control scheme for PWM converter under unbalanced input voltage conditions[J]. IEEE Transactions on Industrial Electronics,1999, 46(5) : 953-959.

[13] 王鹏伍, 崔翔. MMC-HVDC三相解耦二次谐波环流抑制算法[J]. 电力系统自动化, 2013, 37(15): 47-50.

Wang Pengwu, Cui Xiang. Three phases decoupled second harmonic circulation suppression algorithm for MMC-HVDC[J]. Automation of Electric Power Systems, 2013, 37(15): 47-50.

[14] 赵成勇, 胡静, 翟晓萌, 等. 模块化多电平换流器桥臂电抗器参数设计方法[J]. 电力系统自动化,2013, 21(35): 89-93.

Zhao Chengyong, Hu Jing, Zhai Xiaomeng, et al. A parameter design method of bridge arm reactor in modular multilevel converter[J]. Automation of Electric Power Systems, 2013, 21(35): 89-93.

[15] 丁冠军, 汤广福, 丁明, 等. 新型多电平电压源换流器模块化的拓扑机制与调制策略[J]. 中国电机工程学报, 2009, 29(36): 1-6.

Ding Guanjun, Tang Guanfu, Ding Ming, et al.Topology mechanism and modulation scheme of a new multilevel voltage source converter modular[J].Proceedings of the CSEE, 2009, 29(36): 1-6.

[16] Konstantinou G S, Ciobotaru M, Agelidis V G. Operation of a modular multilevel converter with selective harmonic elimination PWM[C]. Proc. IEEE 8th ICPE ECCE, 2011: 999 -1004.

[17] Kui W, Li Yongdong, Zheng Zedong. Voltage balancing control and experiments of a novel modular multilevel converter[C]. IEEE Energy Conversion Congress and Exposition (ECCE), 2010: 3691-3696.

[18] Zhang Yushu, Adam G P, Lim T C, et al. Analysis and experiment validation of a three-level modular multilevel converters[C]. IEEE 8th International Conference on Power Electronics and ECCE Asia (ICPE& ECCE), 2011: 983-990.

[19] Adam G P, Finney S, Williams B. Analysis of modular multilevel converter capacitor voltage balancing based on phase voltage redundant states[J]. IET Power Electronics J., 2012, 5(6): 726-738.

[20] 李笑倩, 宋强, 刘文华, 等. 采用载波移相调制的模块化多电平换流器电容电压平衡控制[J]. 中国电机工程学报, 2012, 32(9): 49-55.

Li Xiaoqian, Song Qiang, Liu Wenhua, et al. Capacitor voltage balancing control by using carrier phase-shift modulation of modular multilevel converters[J]. Proceedings of the CSEE, 2012, 32(9): 49-55.

[21] Hagiwara M, Nishimura K, Akagi H. A medium voltage motor drive with a modular multilevel PWM inverter[J]. IEEE Transactions on Power Electronics,2010, 25(7): 1786-1799.

[22] Li X Q, Song Q, Li J G, et al. Capacitor voltage balancing control based on CPS-PWM of modular multilevel converter[C]. Proc. IEEE Energy Conversion Congress and Exposition, 2011: 4029-4034.

[23] 朱晋, 韦统振, 霍群海. 一种新型全桥变桥臂型VSC-HVDC变流拓扑[J]. 中国电机工程学报, 2013,33(3): 52-59.

Zhu Jin, Wei Tongzhen, Huo Qunhai. A new fullbridge alternative arm based VSC-HVDC converter[J].Proceedings of the CSEE, 2013, 33(3): 52-59.

[24] Rohner S, Bernet S, Hiller M, et al. Modulation,losses, and semiconductor requirements of modular multilevel converters[J]. IEEE Transactions on Industrial Electronics, 2010, 57(8): 2633-2642.