二极管中点钳位型三电平逆变器—交流电机调速系统的高精度建模与分析

梅 杨 孙 凯 黄 震

（1. 北方工业大学电力电子与电力传动北京市工程中心 北京 100144 2. 清华大学电机系电力系统及发电设备控制和仿真国家重点实验室 北京 100084）

1 引言

近年来，采用三电平逆变器驱动的交流电机调速系统，包括异步电机调速系统和同步电机调速系统，已被广泛应用于机车牵引、轧钢设备、矿井提升、油气管道、风力发电等工业和交通领域，取得了良好的应用效果和经济效益[1-4]。这主要是由于三电平逆变器具有输出容量大、输出电压较高、谐波含量小等优点，驱动交流电机运行时可以通过电机的优化设计进一步减小功率损耗以及转矩脉动引起的轴振动[1]。

在各类三电平逆变器拓扑中，经典的二极管中点钳位式（neutral）拓扑在硬件成本、控制难度和可靠性等诸多方面具有明显的比较优势，因此特别适用于驱动高电压、大容量的交流电机调速系统，且已有比较成熟的产品应用，包括异步电机调速系统、电励磁同步电机调速系统和永磁同步电机调速系统等[1,2,5]。但是，对于三电平逆变器—交流电机调速系统实际产品的设计和开发者来讲，在系统设计阶段对其中电气特性和传动特性进行精确的模拟和仿真，始终是一个非常重要但同时又具有很高难度的工作任务[4-7]。

近年来，国内外学者针对三电平逆变器—交流电机调速系统的仿真和模拟开展了大量的研究工作，包括电路与控制环节的仿真建模、动态负荷特性建模、半实物（硬件在环）的仿真实验方法以及故障状态的分析等，取得了一定的成果[3,4,6-9]。但是，目前两种主要的仿真模拟手段均在不同程度上存在不足：

（1）基于 Matlab/Simulink等仿真软件实现的建模仿真只能在基本波形和趋势上模拟系统的电气特性和调速特性，仅能作为实验验证的参考，既往研究中尤其缺乏对仿真结果和实验结果之间模拟精度的定量分析，因而不能作为精确分析三电平逆变器—交流电机调速系统的辅助设计工具。

（2）半实物（硬件在环）的仿真实验方法虽然可以更为精确地模拟调速系统的动静态特性，但是其硬件成本和实现难度均比较高，不适于在三电平交流调速产品设计阶段作为辅助分析工具使用。

本文针对以往仿真建模研究中的不足，深入地分析了二极管中点钳位型三电平逆变器—异步电机调速系统的运行机理、调制方式和控制策略，充分考虑了影响仿真模拟精度的关键要素，建立了完整的三电平调速系统仿真模型，并与实验样机上的测试数据进行了对比。

图1 三电平二极管中点钳位型逆变器—交流电机调速系统Fig.1 Three-level NPC inverter fed AC motor drive system

2 三电平逆变器—交流电机调速系统的仿真建模精度分析

三电平逆变器—交流电机调速系统的仿真工作主要包括三部分内容：①逆变器主电路的建模；②电机及负载的建模；③控制环节的建模。而考察仿真模型对实际系统的模拟精度可以发现，其误差主要来源于以下三方面：

（1）主电路中 IGBT开关过程的仿真建模。在以往的三电平逆变器仿真研究中，主要是为了验证控制策略，因此 IGBT的模型往往被简化为理想开关器件。但实际上 IGBT的开通、关断过程对三电平逆变器的输出性能（电压、电流谐波含量）有明显的影响，同时逆变器输出电压、电流中含有的谐波成分会在交流电机中产生相应的谐波转矩，从而引起电机轴的振动。因此，为了更加真实的反映三电平逆变器的输出特性，需要在系统的仿真建模中采用较为详细的IGBT模型。

（2）考虑死区时间设定的三电平逆变器空间矢量脉宽调制过程仿真建模。空间矢量脉宽调制是三电平逆变器的基本控制方法，逆变器的运行过程中共涉及27个空间矢量，整个调制过程比较复杂[10,11]。而在以往的仿真研究中，对空间矢量的选择与排列已有成熟的建模分析方法，但是死区时间的设定往往被忽略。在实际系统中，死区时间对三电平逆变器的输出谐波含量有显著的影响。因此，为了获得高精度仿真分析模型，需要在仿真建模中设置死区时间模块。

（3）交流电机的空载转矩仿真建模。在交流电机调速系统的仿真建模过程中，负载转矩的大小是可以准确确定的，但实际运行中存在的空载转矩虽然与额定负载转矩相比绝对值和占比均不大，但在电机轻载运行时若忽略空载转矩仍将严重影响电机调速性能的计算精度。因此，在三电平逆变器—交流电机调速系统的高精度仿真建模中，准确地模拟空载转矩的数值也是必须完成的关键任务之一。

3 基于Simulink的三电平逆变器—异步电动机调速系统的精确仿真分析模型

本文所研究的三电平逆变器—异步电机调速系统仿真分析模型是基于Matlab/Simulink的SimPower Systems模块集建立的。如第 2节所述，整个系统仿真分析模型包括三部分：主电路模型、电机及负载模型和控制器模型。

3.1 主电路模型

本文所研究系统中主电路采用的是经典的二极管中点钳位型三电平拓扑。为了完成完整的系统仿真分析，主电路模型由四部分组成（见图2）：①三相可编程交流电压源，用以模拟电网；②三相二极管不控整流桥，用以将三相交流电整流为直流电；③直流母线滤波电容，用以平滑直流电压；④基于12组 IGBT开关器件的二极管中点钳位型（NPC）逆变电路。

图2 主电路模型Fig.2 Model of the main circuit

在主电路模型中，开关器件 IGBT的模型是最为关键的环节。为了克服以往研究中采用理想开关模型模拟 IGBT器件开关过程带来的偏差，本文中采用了SimPowerSystems中详细的IGBT模型以及反并联二极管的模型。模型中可以设定并调整的关键参数包括 IGBT的等效内阻、正向导通压降、电流下降时间、电流拖尾时间、缓冲吸收电阻等以及二极管的等效内阻、正向导通压降、缓冲吸收电阻等。上述参数可以通过所采用功率器件的数据手册获取。所研究系统采用的 IGBT型号为 Fairchild FGL40N60UFD，二极管型号为Microsemi APT60—D60BG。因此，模型中设定的参数见表1。

表1 功率器件参数设置Tab.1 Parameter setting of power devices

3.2 电机及负载模型

在三电平逆变器—异步电机调速系统中，为了模拟不同的负载转矩特性，通常采用直流发电机与异步电机同轴连接组成对拖实验系统。异步电机工作在电动机模式驱动直流发电机，而直流发电机产生的电能最终通过连接在电枢绕组上的电阻消耗掉。

在本文所建立的三电平逆变器—异步电机调速系统仿真模型中，以Simulink中的异步电机和直流电机的标准模型为基础，对其中的关键参数设置进行了优化和处理，以期达到高模拟精度的目标。

对于异步电机，其额定功率、额定电压、额定频率以及极对数等主要参数可以直接从电机铭牌获取，而其他电机参数则需要通过空载试验和堵转试验等手段量测获取，如定转子电阻、定转子电感。但是，转动惯量参数的获取则需采用另外一种量测计算方法。第1步，使直流电机工作在电动机模式以额定电压运行，并驱动异步电机旋转；第2步，记录不同转速下的电枢电流；第3步，通过线性拟合的方法确定电机转速与电枢电流之间的关系，可以用下式表示

因此，电机运行时的空载转矩可通过下式得到

式中，KT为转矩常数；a为摩擦系数；b为空载转矩。

第4步，使异步电机工作在高转速以驱动直流发电机空载运行，逐步降低电机转速。由于电磁转矩为0，则此减速过程可通过下式描述

为了求解式（3），转速变化规律可如下得到

式（4）可以转换为另一种形式

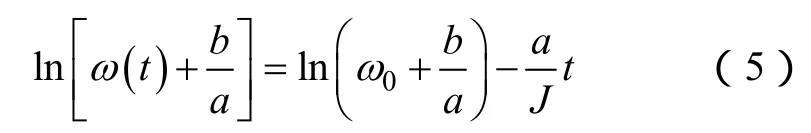
式中，a/J以及转动惯量系数可以通过线性拟合方法得到。

此外，在建模过程中电机的杂散损耗也需考虑。根据经验值，在实际负载转矩值基础上提高 5%以模拟杂散损耗带来的转矩增加。

对于直流发电机，电枢绕组的电阻、电感和励磁绕组的电阻、电感均可以通过直接测量获得。而电枢绕组与励磁绕组之间的互感则需要通过如下步骤得到：第一步，使直流电机在额定励磁电压下空载运行；第二步，在不同转速下测量励磁绕组电流和电枢绕组电压；第三步，根据电枢绕组电压和转速的测量数据利用线性拟合方法得到电压常数KE；第4步，由励磁绕组电流除以KE可以得到电枢绕组与励磁绕组之间的互感值。

3.3 控制器模型

三电平逆变器—交流电机调速系统的控制器通常包括逆变器脉宽调制（如常用的空间矢量脉宽调制）和电机控制（如常用的矢量控制或直接转矩控制）两个环节。异步电机、永磁同步电机等交流电机的高性能控制方法已有完整的仿真建模，在此不赘述[12]。本文将详细介绍三电平逆变器空间矢量脉宽调制策略（SVPWM）的仿真建模过程。

由于可使交流电机实现圆形磁链轨迹及较好的调速性能，空间矢量脉宽调制策略已被广泛应用于交流电机变频调速系统中。在三电平逆变器的调制过程中，共有 27个开关状态相对应的电压空间矢量。利用式（6）可构成空间矢量六边形，如图3所示。

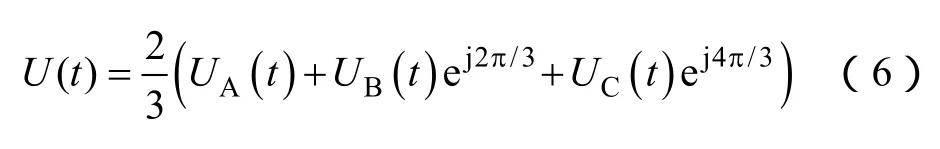
式中，UA、UB、UC分别代表三相桥臂中点与中性点O之间的电压。

如图3所示，空间矢量六边形被27个基本电压矢量分成24个三角形区域。这27个基本电压矢量可被分为四类：6个长矢量的顶点分别位于大六边形的 6个顶点；6个中矢量的顶点分别位于大六边形的6个边上；12个小矢量（包括6个正小矢量和6个负小矢量）的顶点分别位于内部小六边形的 6个顶点上；3个零矢量位于六边形的原点。

当参考电压矢量Vref旋转至空间中某一小三角形区域内时，可利用该小三角形3个顶点上的基本电压矢量合成参考电压矢量。调制过程中采用了七段式模式，即每个开关周期包括7个开关状态对应的基本电压矢量。而且，为了将少基本电压矢量切换时带来的电压跳变，每个开关周期中的第一个基本电压矢量均为负小矢量。

图3 三电平逆变器的电压空间矢量Fig.3 Voltage space vector diagram of three-level inverters

本文基于Simulink构建了详细完整的SVPWM模型，从给定参考电压矢量到的第12个开关器件的驱动信号，整个仿真建模分5步完成。

第 1步（Step1），根据参考电压矢量Vref的幅值和频率计算Vα和Vβ。

第 2步（Step2），确定参考电压矢量Vref顶点所处的大扇区。整个大空间矢量六边形根据相角共分为6个大扇区。在本文的工作中，这一任务由Matlab中的用户定义嵌入性功能模块“Outer_ Sector_Judge”来实现。该功能模块的输入量为Vα和Vβ，而输出量为参考电压矢量所处的大扇区号（1～6）。

第 3步（Step3），确定参考电压矢量Vref顶点所处的小三角形区域。每个大扇区可以被划分为 4个小三角形区域。参考电压矢量Vref顶点所处的具体位置可由Vα和Vβ的相对几何关系计算得到。在本文的工作中，这一任务由 Matlab中的用户定义嵌入性功能模块“Inner_Sector_Judge”来实现。该功能模块的输入量为参考电压矢量所处的大扇区号和Vα、Vβ，而输出量为参考电压矢量所处的小三角形区域号（1～24）。

第 4步（Step4），确定每个开关周期中各个基本电压矢量的作用时间及顺序。为了缩短仿真过程中的计算时间，可以预先根据Vα、Vβ计算好相应的电压矢量作用时间以及作用顺序，存入数据表格中，在仿真程序运行时采用查表的方式获得当前开关周期的作用时间及顺序数据。这一任务也是由Matlab中的用户定义嵌入性功能模块“Time_Calculate”来实现的。该功能模块的输入量为参考电压矢量所处的小三角形区域号和Vα、Vβ，而输出量为开关器件的调制信号波（S1,S3和S2,S4）。其中“-1”表示100%Ts而“1”表示 0%Ts。

第 5步（Step5），将调制信号波转换为所有开关器件的驱动信号。这一任务由Simulink中的比较模块实现。该模块的输入量为调制波和载波，而输出为开关器件的驱动信号。为了准确地描述实际系统中的死区效应，在此设置了一个死区时间模块（死区时间 2.0μs）。此外，处于上升沿和处于下降沿的死区时间并不相同，可以分别设定在仿真建模中，系统的开关频率设为5kHz，而离散系统的全局采样时间设为2.0μs。

4 仿真模型的实验验证

4.1 实验平台

为了充分验证所建立仿真模型的准确性，本文专门搭建了一套二极管中点钳位型三电平逆变器—异步电机调速系统实验平台，并将实验测试结果与基于仿真模型的仿真结果进行了全面细致的比较，重点考察了调速系统的稳态特性、动态特性和谐波特性。

实验平台的构成与图2所示主电路结构相同，主要包括交流电源、二极管整流桥、直流母线、二极管中点钳位型三电平逆变器、异步电机和直流电机负载。在实验和仿真对比中，实验平台的关键参数和仿真模型中设置的参数完全一致，见表2。实验平台照片如图4所示。

图4 实验平台照片Fig.4 Photo of the experimental platform

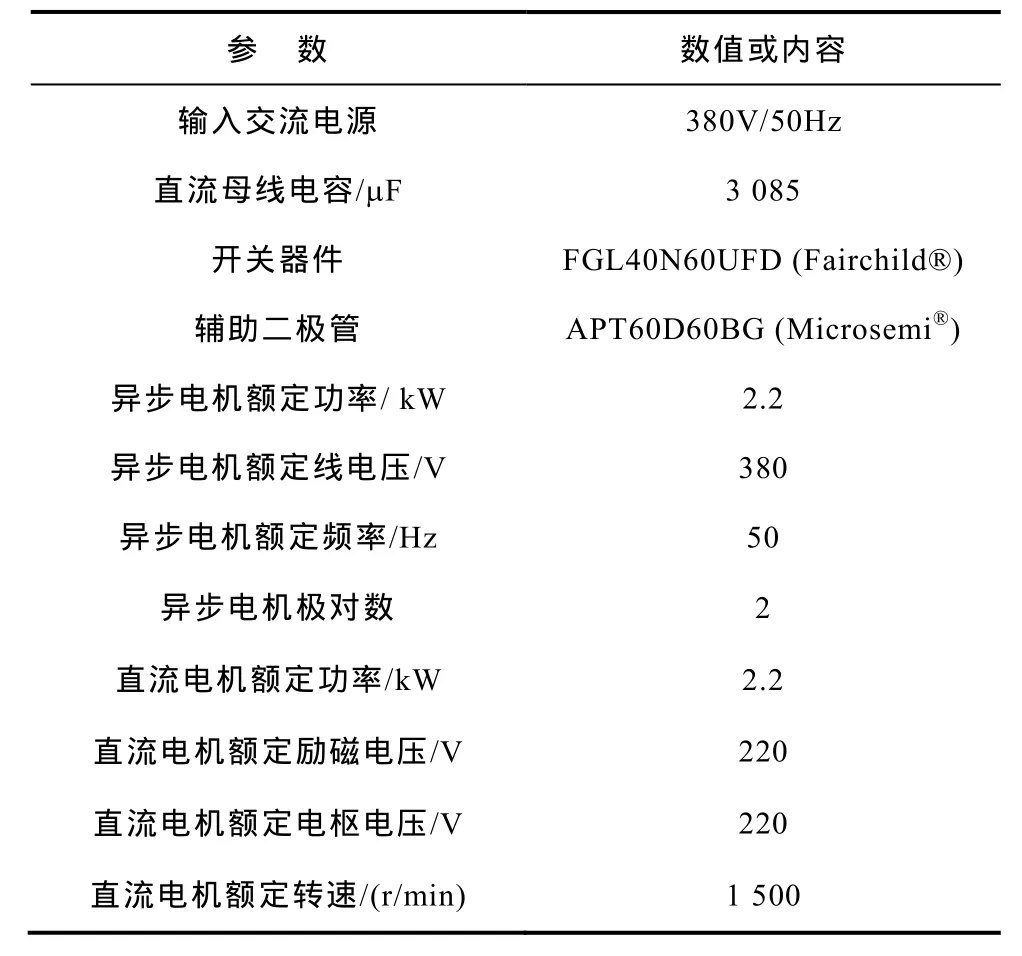
表2 仿真模型和实验平台中的关键参数Tab.2 Key parameters in the simulation model and the experimental platform

4.2 稳态特性的比较验证

稳态特性的比较工况包括3个不同的异步电机定子频率值（50Hz、25Hz、5Hz）。每一工况下包含3个工作点，分别为100%、75%和50%额定负载转矩。比较结果见表3～表5。

表3 稳态特性的比较结果（50Hz）Tab.3 Comparison results on steady-state characteristics(50Hz)

表4 稳态特性的比较结果（25Hz）Tab.4 Comparison results on steady-state characteristics(25Hz)

图5给出了系统在额定工况稳态运行时的仿真和实验波形比较，包括三电平逆变器输出的三相线电压和三相线电流波形。

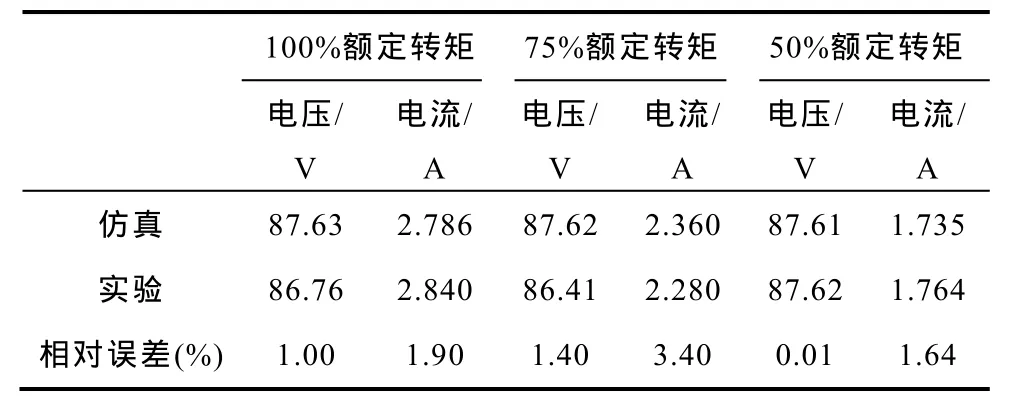
表5 稳态特性的比较结果（5Hz）Tab.5 Comparison results on steady-state characteristics(5Hz)

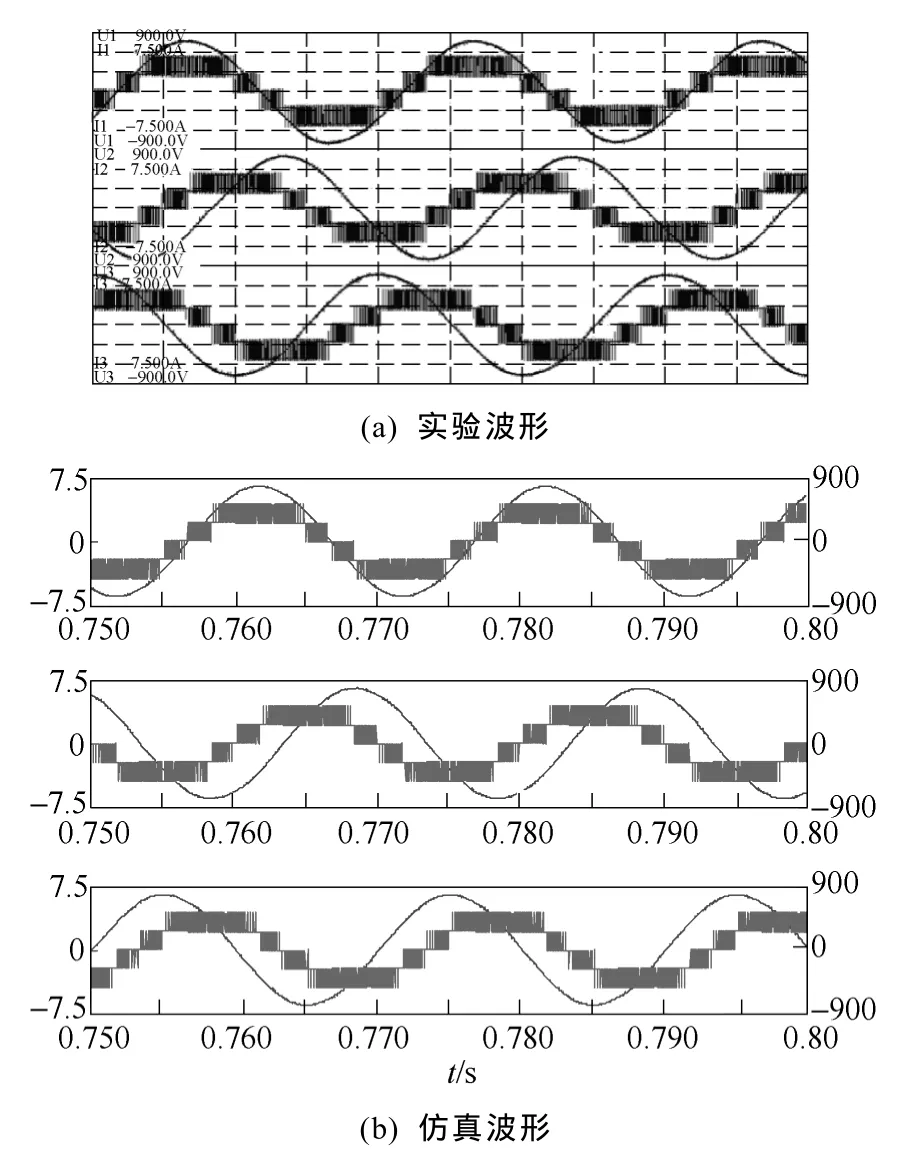
图5 额定工况下逆变器输出线电压、线电流的波形比较Fig.5 Comparison of the output line-line voltages and phase currents at the rated condition

从以上的比较结果可以看出，本文所建立的三电平逆变器—异步电机调速系统仿真模型在稳态运行工况下具有非常高的模拟精度。与实测结果相比，三电平逆变器输出电压、电流（即异步电机定子电压、电流）的相对模拟误差全部小于4%。

4.3 动态特性的比较验证

动态特性的比较工况也包括3个不同的异步电机定子频率值（50Hz、25Hz、15Hz）。为了更好的评估系统仿真模型在动态条件下的模拟精度，本文采用了负载转矩突变情况下电机电流幅值整定时间这一评估指标，即负载转矩从额定值跳变为空载和从50%额定值跳变为空载时电机电流幅值的整定时间（从转矩突变时刻开始至重新进入稳态的时间）。电机电流幅值的计算公式为

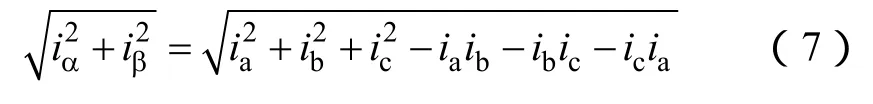
为了滤除噪声信号的影响，在 Matlab中对仿真数据和实验数据均采用了相同参数的 Butterworth低通滤波器进行处理。图6给出了当负载转矩从额定值跳变为零时的波形比较，电机定子频率为 25Hz。

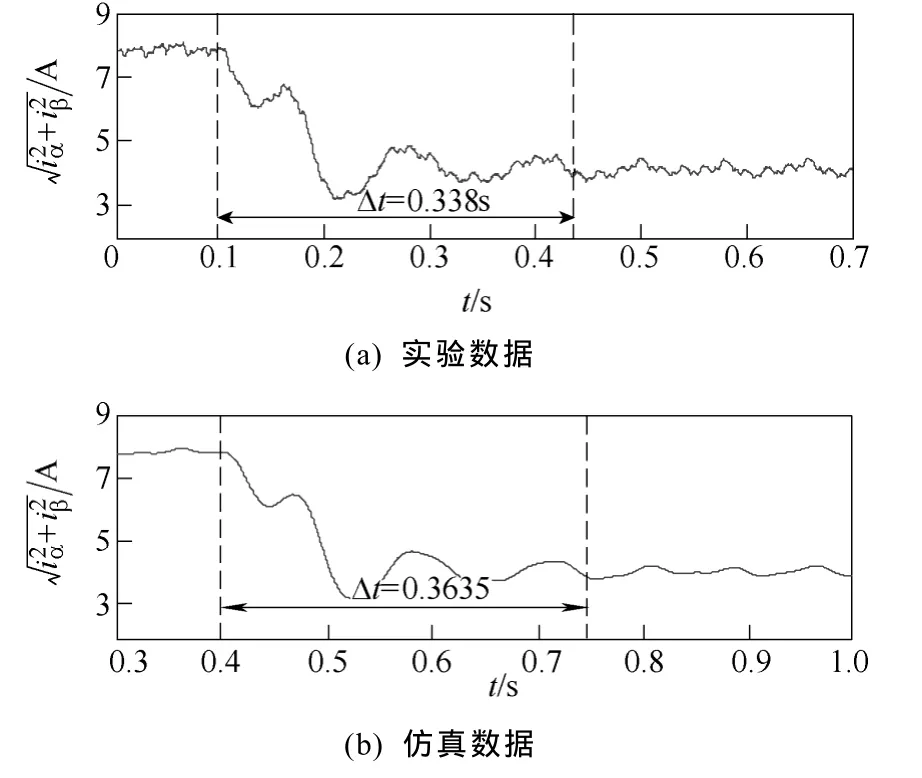
图6 负载转矩突变情况下（100%→0%）电机电流幅值动态变化波形比较（25Hz）Fig.6 Comparison of the dynamic waveforms of the motor current amplitude when load torque changes from 100% to 0% at the frequency 25Hz

图7 负载转矩突变情况下（0%→100%）电机电流幅值动态变化波形比较（15Hz）Fig.7 Comparison of the dynamic waveforms of the motor current amplitude when load torque changes from 0% to 100% at the frequency 15Hz

不同工况下详细的动态特性比较结果见表 6。从表中可以看出，本文所建立的三电平逆变器—异步电机调速系统仿真模型在动态运行工况下亦具有非常高的模拟精度。与实测结果相比，三电平逆变器输出电流（即异步电机定子电流）整定时间的相对模拟误差全部小于9%。

表6 动态特性的比较结果Tab.6 Comparison results on dynamic characteristics

4.4 谐波特性的比较验证

谐波特性的比较验证是在额定工况下进行的。在仿真和实验中分别采集了逆变器输出电流（即电机定子电流）的数据，并利用快速傅立叶变换（FFT）计算出总谐波畸变率（THD）。

图8中给出了分别由实测数据和仿真数据计算得到的谐波频谱（放大后）。实验中电机定子电流的THD为1.02%，而仿真中电机定子电流的 THD为0.91%，二者的相对误差仅为 10.78%。从上述结果可以看出，本文所建立的三电平逆变器—异步电机调速系统仿真模型在谐波特性模拟方面也具有非常高的精度。

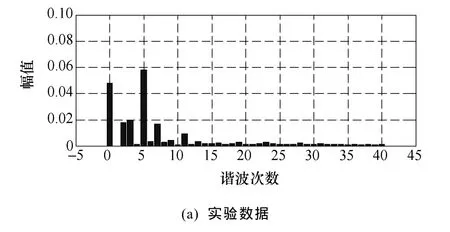
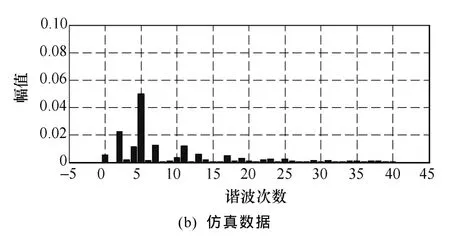
图8 谐波频谱比较Fig.8 Harmonic spectrum contrast

5 结论

本文基于 Matlab/Simulink建立了一个二极管中点钳位型三电平逆变器—异步电机调速系统的仿真分析模型。根据该模型得到的仿真结果与实验样机上测得的实验结果进行了全面的比较验证，考察了稳态特性、动态特性和谐波特性。

比较结果表明，本文所建立的仿真分析模型具有非常高的模拟精度，可以用作三电平逆变器—交流电机调速系统的设计工具。在产品的设计阶段，即可以对该调速系统进行优化设计，以获得良好的动静态性能。

[1] 李永东, 肖曦, 高跃. 大容量多电平变换器——原理·控制·应用[M]. 北京: 科学出版社, 2005.

[2] 谭国俊, 吴轩钦, 李浩, 等. Back-to-Back 双三电平电励磁同步电机矢量控制系统[J]. 电工技术学报,2011, 26(3): 36-43.

Tan Guojun, Wu Xuanqin, Li Hao, et al. Vector control system of electrically excited synchronous motor fed by Back-to-Back dual three-level converter[J]. Transactions of China Electrotechnical Society, 2011, 26(3):36-43.

[3] 周京华, 贾斌, 章小卫, 等. 混合式三电平中点电位平衡策略[J]. 中国电机工程学报, 2013, 33(24): 82-89.

Zhou Jinghua, Jia Bin, Zhang Xiaowei, et al. A hybrid three-level neutral-point balance control strategy[J].Proceedings of the CSEE, 2013, 33(24): 82-89.

[4] 韩坤, 冯晓云, 葛兴来, 等. 动车组牵引电动机全速域控制的研究与仿真[J]. 电工技术学报, 2011,26(S1): 297-302.

Han Kun, Feng Xiaoyun, Ge Xinglai, et al. Research and simulation on full speed range control of EMU traction motor[J]. Transactions of China Electrotechnical Society, 2011, 26(S1): 297-302.

[5] Nabae A, Takahashi I, Akagi H. A new neutral-pointclamped PWM inverter[J]. IEEE Transactions on Industry Applications, 1981, 17(5): 518-523.

[6] 苏天诺, 邹明轩, 彭光强, 等. 基于统计综合法和三电平特性的高速动车组暂态负荷建模[J]. 电工技术学报, 2014, 29(6): 257-262.

Su Tiannuo, Zou Mingxuan, Peng Guangqiang, et al.Transient load modeling of high speed multiple units based on the statistical syntheses method and threelevel characteristics[J]. Transactions of China Electrotechnical Society, 2014, 29(6): 257-262.

[7] 宋文胜, 冯晓云, 侯黎明, 等. 电力牵引传动系统的三电平直接转矩控制算法的半实物实验研究[J].电工技术学报, 2012, 27(2): 165-172.

Song Wensheng, Feng Xiaoyun, Hou Liming, et al.Hardware-in-loop research of three-level direct torque control scheme for electric traction drive system[J].Transactions of China Electrotechnical Society, 2012,27(2): 165-172.

[8] 陈丹江, 叶银忠, 华容. 基于波形实时分析的动车组三电平逆变器故障诊断技术[J]. 电工技术学报,2014, 29(6): 106-113.

Chen Danjiang, Ye Yinzhong, Hua Rong. Fault diagnosis for three-level inverter of CRH based on realtime waveform analysis[J]. Transactions of China Electrotechnical Society, 2014, 29(6): 106-113.

[9] Bor Ren Lin. Analysis and implementation of a threelevel PWM rectifier/inverter[J]. IEEE Transactions on Aerospace and Electronic Systems, 2000, 36(3): 948-956.

[10] Mondal S K, Bose B K, Oleschuk V, et al. Space vector pulse width modulation of three-level inverter extending operation into overmodulation region[J].IEEE Transactions on Power Electronics, 2003, 18(2):604-611.

[11] Kocalmis A, Sunter S. Simulation of a space vector PWM controller for a three-level voltage-fed inverter motor drive[J]. Proceedings of IEEE IECON, 2006:1915-1920.

[12] 李永东. 交流电机数字控制系统[M]. 2版.北京: 机械工业出版社, 2012.