两相静止坐标系下消除不对称和谐波影响的同步信号提取方法

杜 雄 王国宁 孙鹏菊 周雒维

（重庆大学输配电装备及系统安全与新技术国家重点实验室 重庆 400030）

1 引言

三相并网变流器在新能源发电和电能质量治理领域中得到了广泛的应用[1-3]。三相并网变流器可以在两相旋转坐标系下进行控制，如单通道dq坐标系和双通道dq坐标系下采用比例积分（PI）调节器进行电流调节[4-6]；也可在三相和两相静止坐标系下采用PI或比例谐振（PR）调节器进行控制[6,7]，在三相三线制系统中，两相静止坐标系下的控制相比三相静止坐标系更加简单。无论是两相旋转坐标系，还是两相静止坐标系下的控制，为了实现并网电流的谐波抑制，有功无功功率的控制，都需要能够快速准确地检测出电网电压的同步信号，即基波电网电压正负序分量的幅值和相位信息[8-11]。

电网电压的同步信号检测方法包括基于瞬时对称分量分解的延时信号检测法，同步参考坐标系锁相环，自适应陷波器，卡尔曼滤波器等方法[12-17]。其中基于同步参考坐标系锁相环和基于自适应陷波器锁相环的两类方法是比较有代表性的方法[14,16]。基于同步参考坐标系变换的锁相环（SRF-PLL）将三相电压转换到两相同步旋转dq坐标系，通过引入q轴分量的反馈实时调节相位信息，可以得到直流dq轴分量[14]，检测结果适合于旋转坐标系下的三相并网变流器的控制。基于自适应陷波器（ANF）和二阶广义积分器（SOGI）的这一类同步信号提取方法在三相静止坐标系或两相静止坐标系下通过二阶陷波器得到基波分量，该方法得到的是在静止坐标下的正弦同步信号[16,18]，适合于静止坐标下的三相变流器的控制。

在同步信号提取中，在三相电源电压对称且无谐波的情况下，相对容易得到同步信号。但实际工况中，电网电压均含有谐波分量以及不同程度的不对称，特别在电网故障情况下，不对称程度更加严重。为了消除不对称的影响，同步旋转坐标系锁相环可以采用解耦双通道 dq旋转坐标系来实现正负序分量分离[19]，采用多通道 dq旋转坐标系来消除谐波的影响[20]，但该类方法需要经过三角函数运算，其计算相对复杂。自适应陷波器方法通过在两相静止坐标系下分别采用二阶陷波器来得到基波分量，为了得到正负序分量，还需利用瞬时对称分量法来进行正负序的分离；为了消除谐波分量的影响，在每个谐波通道均需增加两个二阶陷波器，这也较大地增加了系统的阶数和复杂性[16,18]。另外同步信号的提取还需考虑电源频率变化的影响[8]。

本文主要针对在两相静止坐标下的同步信号提取方法进行研究，通过采用正弦幅值积分器来直接得到正序和负序分量，无需解耦和正负序分离。为了消除某次谐波的影响，只需增加一个正弦幅值积分器，系统阶数只增加二阶，可以更加简单地实现同步信号提取。文中通过采用多通道正弦幅值积分器，消除了电网电压不对称和谐波的影响，构造了电源频率自适应算法来消除电源频率变化的影响。文中讨论的同步信号检测结果可直接应用于静止坐标系下的三相变流器的控制，如需用于旋转坐标系下的控制，可经过简单的算术运算得到正负序 dq轴直流分量，无需进行三角函数运算。

2 基于多通道正弦幅值积分器的同步信号检测方法

2.1 正弦幅值积分器

正 弦 信 号 对 时 间 的 积 分 ， 如 ∫Acos(ωt)dt=，实际上实现的是正弦信号幅值和相位的变换，并没有实现类似直流信号对时间的积分的数学关系，如∫Cdt=Ct。如果能够实现对正弦信号的幅值进行时间的积分，如输入为xin=Ac os(ωt)，输出为yin=Ac os(ωt)t，则可通过该幅值积分器来实现对正弦信号的零误差跟踪，实现这一关系的积分器称为正弦幅值积分器（Sinusoidal Amplitude Integrator，SAI）[21,22]。当两个输入信号存在正交关系时，可以用图1所示的电路来构造正弦幅值积分器。

图1 正弦幅值积分器Fig.1 The sinusoidal amplitude integrator（SAI）

图1中输入输出满足关系

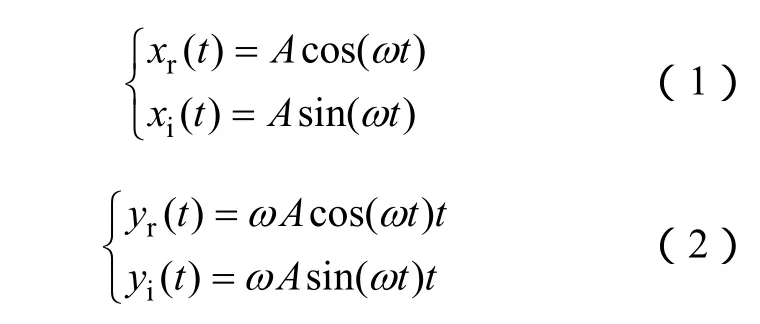
从上式可以看出，图1实现了对输入正弦信号幅值的积分。为了简化分析，可以将输入输出写成如下复数形式

对图1所示的输入和输出关系进行Laplace变换，可以应用复系数传递函数来进行描述[22]

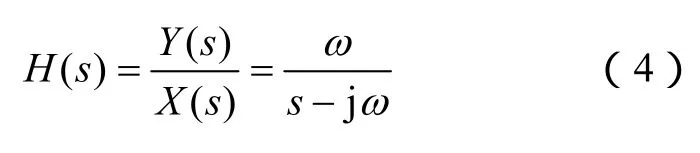
相对应还可以构造负频率的正弦幅值积分器，其传递函数可描述为

式（4）和式（5）可以看出正弦幅值积分器具有正负频率选择特性，可以用于三相电压在不对称和含有谐波等畸变条件下的同步信号提取。从前述分析可以看出，应用SAI的两个关键之处是：①输入信号具有式（1）的正交关系；②能够准确地得到输入信号的频率。

2.2 电网电压在含有谐波和不对称时的矢量描述

为了能够将三相电网电压转换为具有正交关系的数学表述，可以对其进行三相静止坐标系到两相静止坐标系的坐标变换，然后构造电压矢量。

三相电压不对称，且含有谐波时，忽略零序分量时，三相电压可表示为

式中，V+1、V-1分别为正、负序基波分量的幅值；φ-1为负序分量的相位，当h＜-1时，Vh和φh为负序谐波分量的幅值和相位，当h＞1时，Vh和φh为正序谐波分量的幅值和相位。

将三相电压变换到两相αβ坐标系，可得

从式（7）可以看出，三相电压变换到两相静止坐标系中，αβ分量具有正交关系，满足应用 SAI的条件（1）。

虽然理论上电压含有从-∞到+∞的无穷次谐波分量，但在实际电网电压中，电网电压一般除基波正负序分量外，还含有 6k±1次的谐波分量，其中在实际的电网内，6k-1次谐波分量一般为负序分量，6k+1次谐波一般为正序分量。

2.3 基于多通道SAI的同步信号检测

由于实际电网电压中高次谐波分量含量一般较小，因此一般可只考虑低次谐波的影响，文中主要考虑了-5、+7次谐波的影响，如果根据实际需要还可加入其他谐波的影响。为了消除谐波的影响，文中构造的基于多通道SAI的同步信号检测方法如图2所示。

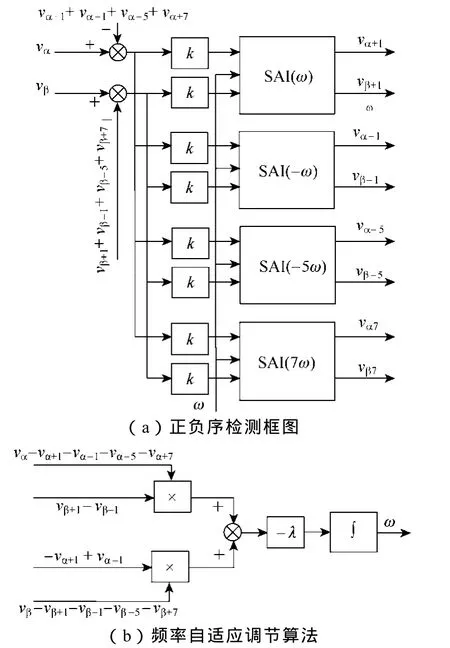
图2 采用SAI的同步信号检测框图Fig.2 The block diagram of grid synchronization signal detection based on SAI

图中三相电压经过 3-2变换后得到αβ分量(vα,vβ)，作为同步检测单元的输入，包括四个SAI单元，分别是正序 SAI(ω)，负序 SAI(-ω)，5 次 SAI(-5ω)单元和7次单元 SAI(7ω)。四个SAI单元的输出分别为提取的正序分量，负序分量，5次谐波分量，7 次谐波分量的αβ 轴分量(vα+1,vβ+1)，(vα-1,vβ-1)，(vα-5,vβ-5)，(vα+7,vβ+7)，其中k为同步信号提取的调节参数，为正实数，ω为频率自适应调节单元输出的角频率信号，用于实时调节SAI的中心频率。如果不考虑谐波分量，则可将5次SAI(-5ω)单元和7次单元SAI(7ω)去掉。

频率自适应调节算法的框图如图2b所示，根据输入输出信号经过简单的算术运算，通过一个积分环节得到频率信息，其中λ为频率调节参数。在下一节中将通过建立数学模型对同步信号提取的机理和参数选取进行分析。

3 数学模型与机理分析

3.1 正负序分量检测机理

在考虑系统达到稳态的情况下，近似认为该系统为一时不变系统，可以采用线性系统理论对其进行近似分析。定义图2对应的复频域复向量分别为

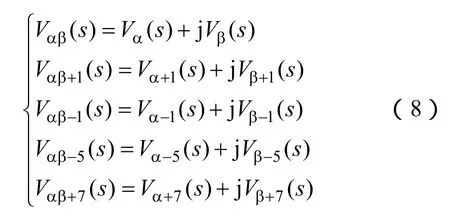
图 2中 SAI(ω)、SAI(-ω)、SAI(-5ω)和 SAI(7ω)的传递函数分别为Tf+1(s)、Tf-1(s)、Tf-5(s)和Tf+7(s)

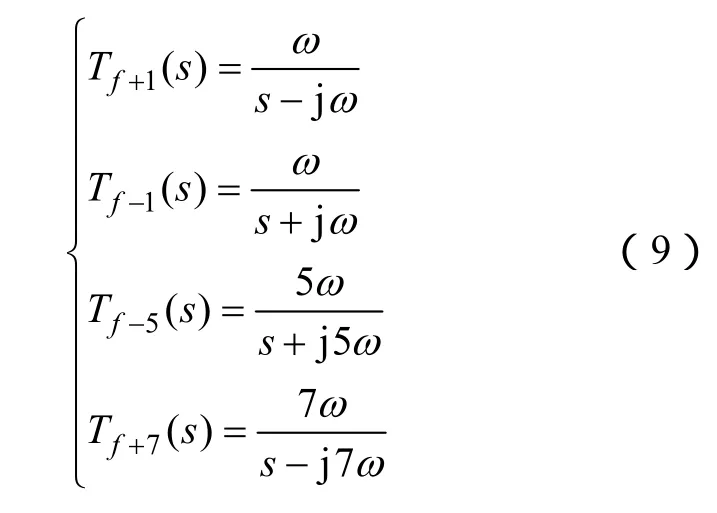
根据图2所示的同步信号检测框图可以通过上述复向量来建立频率模型

可以得到每个通道的输入输出传递函数为

虽然上式仅考虑-5、7次谐波的影响，还可考虑更多次数的谐波分量，比如考虑±1、-5、7、-11、+13次谐波影响，的基波正序分量传递函数的频域特性如图3所示。

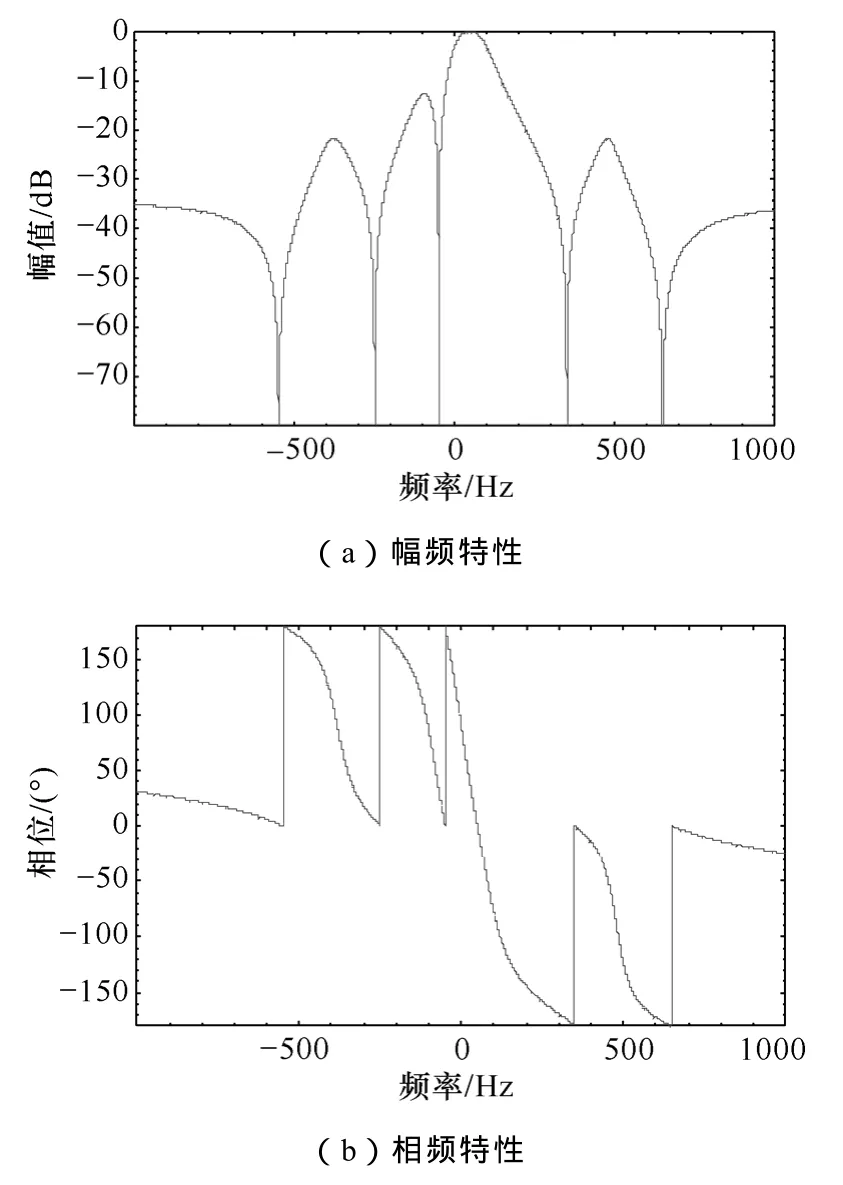
图3 正序基波分量的频率响应Fig.3 The frequency response of the positive –sequence fundamental component

从图3可以看出，除+50Hz幅值增益为 0外，在-50Hz，-5、7、-11、13谐波出的增益均为-∞，说明该方法可以无衰减的检测出正序分量，而对其他分量则可以实现全衰减，且在特征频率处的相位为 0，说明基波正序分量的检测没有相位差。可以得到相类似的负序基波分量的频域特性。因此在稳态情况下，可以准确的提取出正序和负序分量的αβ分量，利用αβ分量可以得到正序分量和负序分量的幅值和相位信息。

为了对同步信号检测参数进行设计，对图3的频率特性和只含有正、负两个通道的频率特性进行了对比，如图4所示。

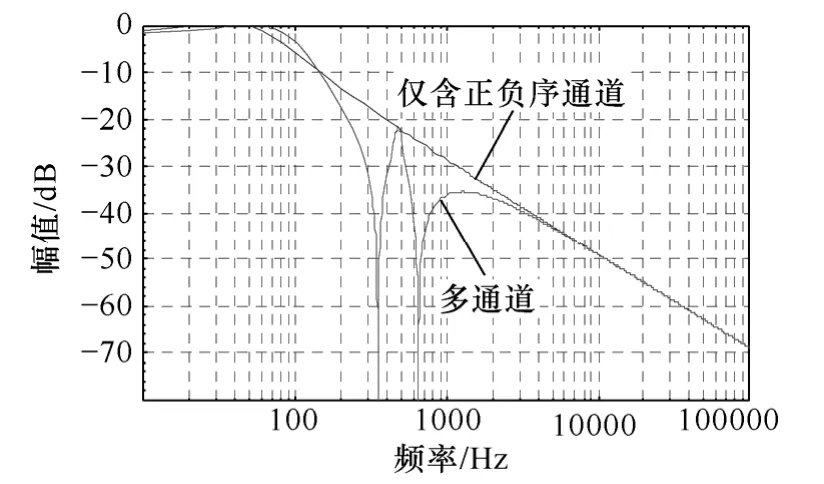
图4 频率响应对比Fig.4 The comparison of frequency responses

从图4可以看出，多通道方法除在特定次数的谐振频率点之外，具有和二阶系统相类似的频域特性，可参考二阶系统的频率特性来设计。仅含正负序通道的二阶传递函数为

综合二阶系统的响应速度和超调量，k取比较合适，因此在本文中k便取该值。

3.2 频率自适应机理

为了根据输入输出情况实时调节图 2a中的中心频率，设计了频率自适应算法，如图2b。vα、vβ为SAI的同步信号提取单元的电网电压输入信号，vα+1、vβ+1、vα-1、vβ-1、vα-5、vβ-5、vα+7、vβ+7分别为SAI单元的输出信号，λ为频率自适应调节参数。图2b中的自适应算法可描述为

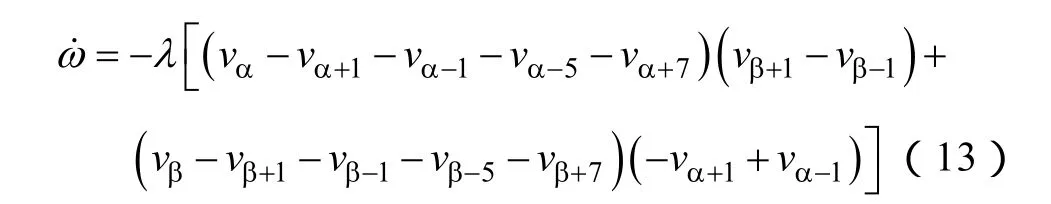
为了简化分析，令输入频率为ω'，忽略谐波分量和负序分量，输入电压可描述为

根据式（15）对式（13）进行化简，即得

式中，G和∠P分别为式（12）中传递函数的幅值和相位增益

式中，m=ωω，在ω'≈ω，即m≈1的情况下，根据式（17），对式（16）可进一步简化为

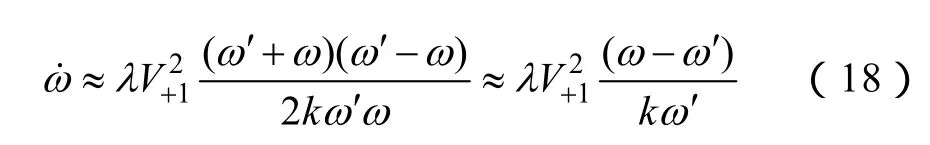
从式（18）可以看出，频率调节过程近似为一个一阶负反馈系统，可以实现频率的自适应动态调节。其时间常数近似为。一般取时间常数τ与电源周期相当，具体的参数选取见下一节实验验证。

4 实验验证

为了验证本文提出的多通道SAI的同步信号检测方法的性能，采用dSPACE PX10实现信号采样和数据处理，数字实现的离散算法为ode1算法，采样频率为 20kHz，输入电源电压信号由可编程三相交流电源61703提供。实验中，输入平衡三相电压幅值为Vp=100V，频率为 50Hz的三相交流电。k取0.707，λ取值为2。

其中，电源中所注入的谐波含量为，5、7次谐波各为10%，11、13次谐波各为 5%。所得的实验波形主要包括，输入电压波形，三相基波电压正负序幅值和基波正负序的相位。

4.1 含谐波的单相电压跌落实验

单相电压跌落时的实验结果如图5所示。图5a为含谐波单相电压跌落时的三相输入电压波形，其中，C相电压幅值跌落50%。图5b显示的是只含正负序双通道SAI结构时提取出的基波正负序分量的幅值和相位，从图中可以看出，提取的幅值和相位分量中中含有部分波动分量，说明谐波对单通道的同步信号检测有一定的影响。在采用多通道SAI方法后，检测结果如图5c所示，此时能够消除谐波的影响，准确地提取出正负序电压幅值和相位信息，响应时间在一个工频周期左右。

图5 含谐波单相电压跌落工况下单通道与多通道SAI同步信号检测比较Fig.5 Comparison on synchronization signal detection of single-channel and multi-channel SAI under single phase drop conditions and containing harmonics

4.2 含谐波的两相电压跌落实验

当电源电压输入含谐波且 B、C两相电压各跌落50%时，其输入波形和经过多通道SAI同步信号的实验结果如图6所示。图6a为含谐波两相电压跌落时的三相输入电压波形，图 6b为提取出的基波正负序分量的幅值和相位。

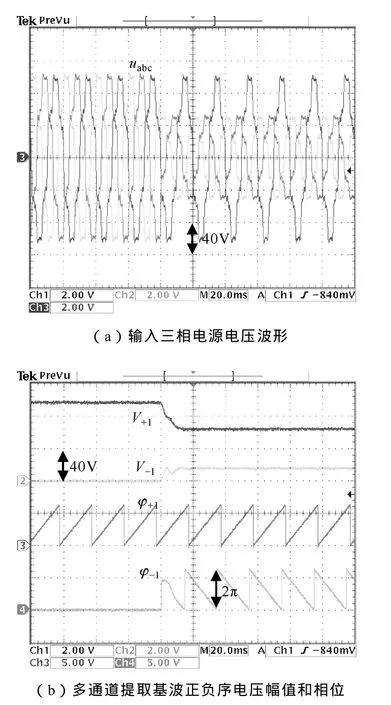
图6 含谐波两相电压跌落工况下同步信号检测结果Fig.6 Synchronization signal detection results under two phases drop conditions including harmonics

从图 6b中可以看出，多通道 SAI同步信号检测方法可以准确的在含谐波且不对称的电源电压中提取出基波的正负序幅值和相位，且响应时间在一个工频周期左右。

4.3 含谐波的电网不对称工况下频率跳变实验

图 7为输入电源电压在含谐波且不平衡工况下，频率从 50Hz上升到 55Hz时的实验波形。图7a中可以看出，输入电压含谐波，且B、C两相电压跌落50%，频率上升5Hz时，可以检测出频率信息，且响应速度在5τ左右，与第3节中的理论分析相吻合。从图7b可以看出，在频率跳变时，正负序电压分量变化较小，仍能够准确快速地提取出基波正负序分量的幅值与相位。

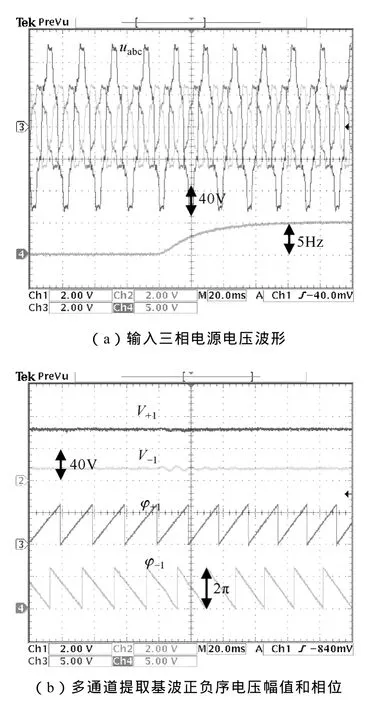
图7 含谐波不平衡工况下频率升高5Hz的实验结果Fig.7 Experimental results when frequency jumps 5Hz under unbalance condition and containing harmonic

5 结论

为了能够获得不对称和含有谐波情况下输入电压的基波正负序幅值和相位信息，本文提出一种在两相静止坐标系，采用基于多通道的正弦幅值积分器的同步信号检测方法。该方法不仅消除了谐波分量，还可以在不对称的情况下，无需进行正负序分离就可以直接得到正序分量和负序分量的幅值和相位信息。本文提供的实验结果表明所提出的同步信号提取方法可以在电源频率变化、不对称以及含有谐波的情况下快速准确出提取出正负序分量的幅值和相位信号。

[1] 涂春鸣, 李慧, 唐杰, 等, 电网电压不对称对D-STATCOM 的影响分析及抑制[J]. 电工技术学报, 2009, 24(8): 114-121.

Tu Chunming, Li Hui, Tang Jie, et al. Analysis and suppression of influence on D-STATCOM under unbalanced voltage of power system[J]. Transactions of China Electrotechnical Society, 2009, 24(8):114-121.

[2] Geng Hua, Yang Geng, Xu Dewei, et al. Unified power control for PMSG-based WECS operating under different grid conditions[J]. IEEE Transactions on Energy Conversion, 2011, 26(3): 822-830.

[3] Li Shuhui, HaskewT A, Williams K A, et al. Control of DFIG wind turbine with direct-current vector control configuration[J]. IEEE Transactions on Sustainable Energy, 2012, 3(1): 1-11.

[4] Moran L, Ziogas P D, Joos D. Design aspects of synchronous PWM rectifier-inverter systems under unbalanced input voltage conditions[J]. IEEE Transactions on Industry Applications, 1992, 28(6): 1286-1293.

[5] Song H S, Nam K. Dual current control scheme for PWM converter under unbalanced input voltage conditions[J]. IEEE Transactions on Industrial Electronics,1999, 46(5): 953-959.

[6] Zmood D N, Holmes D J. Stationary frame current regulation of PWM inverters with zero steady-state error[J]. IEEE Transaction Power Electronics, 2003,18(3): 814-822.

[7] Li Zixin, Li Yaohua, Wang Ping, et al. Control of three-phase Boost-type PWM rectifier in stationary frame under unbalanced input voltage[J]. IEEE Transactions Power Electronics, 2010, 25(10): 2521-2530.

[8] Blaabjerg F, Teodorescuk R, Liserre M, et al. Overview of control and grid synchronization for distributed power generation systems[J]. IEEE Transactions on Industry Electronics, 2006, 53(5): 1398-1409.

[9] Tsili M, Papathanassiou S. A review of grid code technical requirements for wind farms[J]. IET Renewable Power Generation, 2009, 3(3): 308-332.

[10] Geng H, Xu D, Wu B. A novel hardware-based alldigital phase-locked loop applied to grid-connected power converters[J]. IEEE Transactions on Industry Electronics, 2011, 58(5): 1737-1745.

[11] 张桂斌, 徐政, 王广柱. 基于空间矢量的基波正序、负序分量及谐波分量的实时检测方法[J]. 中国电机工程学报, 2001, 21(10): 1-5.

Zhang Guibin, Xu Zheng, Wang Guangzhu. Study and simulation of real-time detecting method for fundamental positive sequence, negative sequence components and harmonic components based on space vector[J].Proceedings of the CSEE, 2001, 21(10): 1-5.

[12] 袁旭峰, 程时杰, 文劲宇. 改进瞬时对称分量法及其在正负序电量检测中的应用[J]. 中国电机工程学报, 2008, 28(1): 52-58.

Yuan Xufeng, Cheng Shijie, Wen Jinyu. An improved method of instantaneous symmetrical components and its detection for positive and negative sequence current[J]. Proceedings of the CSEE, 2008, 28(1): 52-58.

[13] Souza H, Bradaschia F, Neves F, et al. A method for extracting the fundamental-frequency positive-sequence voltage vector based on simple mathematical transformations[J]. IEEE Transactions Power Electronics,2009, 56(5): 1539-1547.

[14] Kaur V, Blasco V. Operation of a phase locked loop system under distorted utility conditions[J]. IEEE Transactions on Industry Applications, 1997, 33(1):58-63.

[15] Guo X, Wu W, Chen Z. Multiple-complex coefficientfilter-based phase-locked loop and synchronization technique for three-phase grid-interfaced converters in distributed utility networks[J]. IEEE Transactions on Industry Electronics, 2011, 58(4): 1194-1204.

[16] Yazdani D, Bakhshai A, Joos G, et al. A nonlinear adaptive synchronization technique for grid-connected distributed energy sources[J]. IEEE Transactions Power Electronics, 2008, 23(4): 2181-2186.

[17] Routray A, Pradhan A K, Rao K P. A novel Kalman filter for frequency estimation of distorted signals in power systems[J]. IEEE Transactions on Instrumentation and Measurement, 2002, 51(3): 469-479.

[18] Rodr´ıguez P, Luna A, Mu˜noz-Aguilar R S, et al. A stationary reference frame grid synchronization system for three-phase grid-connected power converters under adverse grid conditions[J]. IEEE Transactions Power Electronics, 2012, 27(1): 99-112.

[19] Rodriguez P, Pou J, Bergas J, et al. Decoupled double synchronous reference frame PLL for power converters control[J]. IEEE Transactions Power Electronics, 2007,22(2): 584-592.

[20] 李珊瑚, 杜雄, 王丽萍, 等, 解耦多同步参考坐标系电网电压同步信号检测方法[J]. 电工技术学报,2011, 26(12): 183-189.

Li Shanhu, Du Xiong, Wang Liping, et al. A grid voltage synchronizaiton method based on decoupled multiple synchronous reference frame[J]. Transactions of China Electrotechnical Society, 2011, 26(12):183-189.

[21] Yuan X, Merk W, Stemmler H, et al. Stationary frame generalized integrators for current control of active power filters with zero steady-state error for current harmonics of concern under unbalanced and distorted operating conditions[J]. IEEE Transactions Power Electronics, 2002, 38(2): 523-532.

[22] Martin K. Complex signal processing is not complex[J]. IEEE Transactions Circuits and System I: Regular Papers, 2004, 51(9): 1823-1836.