不确定充电习惯对电动汽车充电负荷需求及充电负荷调节的影响

杨 冰 王丽芳 廖承林 吉 莉 董凤宇

（1. 中国科学院电力电子与电气驱动重点实验室 电工研究所 北京 100190 2. 中国科学院大学 北京 100049 3. 国网北京市电力公司 北京 100031）

1 引言

随着化石燃料的消耗殆尽以及环境的恶化，电动汽车的使用将成为一种趋势，而规模化电动汽车的使用必将给电网运行带来不容忽视的影响[1-5]。这些影响可能会由电动汽车充电过程中的不确定性因素引起，因此有必要研究不确定性因素对充电需求及充电负荷调节的影响。

充电负荷需求的计算是电动汽车充电设施规划、未来用户充电行为引导和电动汽车充电负荷调节的基础[4]。电动汽车充电负荷需求类似于其他形式的电力负荷，有着很大程度的不确定性和规律性[6,7]：不确定性是指由于个体电动汽车用户充电时间和充电功率的随机性而引起的充电负荷需求在各时刻的随机波动；规律性是指规模化电动汽车充电负荷需求的整体变化趋势。而用户充电习惯的不确定性和充电功率的不确定性会带来充电负荷需求曲线变化趋势的改变，进而给负荷调节带来一定的影响。现有充电负荷调节的研究中仅考虑了确定性的充电需求及其充电负荷调节策略，包括延迟充电和智能充电等方法[9-14]，这些研究均是考虑如何降低充电负荷对电网影响，却很少有研究充电习惯不确定时充电负荷调节策略，并且很少考虑用户充电能量需求的满足程度，文献[15]中考虑了用户充电能量需求的满足率，但是却认为所有用户的充电能量需求相同。

本论文以充电概率的方法描述电动汽车用户充电习惯的不确定性，建立了考虑不确定性因素的电动汽车充电负荷计算模型，分析了不确定性因素对充电负荷需求和充电负荷调节的影响；提出以充电起始时间和充电功率为控制变量的充电负荷优化调节计算模型。

2 不确定充电习惯建模及充电需求计算方法

2.1 充电习惯不确定性建模

电动汽车用户充电习惯的主观性很强，但是对于单个用户的充电行为，只有两种状态：“行驶结束后即充电”和“不能满足行驶需求时充电”。对于规模化电动汽车集群，充电习惯则呈现出不确定的情况，介于“所有用户行驶结束后充电”和“所有用户行驶结束后且不能满足行驶需求时充电”两种状态之间。将“行驶结束后即充电”用“1”表示，将“不能满足行驶需求时充电”用“0”表示，因此单个用户每天的充电行为服从（0-1）分布。假设用户之间充电行为互不影响，数量为n的电动汽车集群充电习惯将近似服从参数为n、p的二项分布，记为 charge_set～b（n，p），其中p为充电的概率，由于p的取值在区间[0, 1]范围内，因此可认为电动汽车集群的充电概率服从U（0, 1）均匀分布。

电动汽车充电负荷需求计算考虑的是规模化电动汽车集群的充电行为，而对于个体充电行为，可以通过如下的两步进行确定：

（1）设定集群充电概率为p，p∈[0, 1]；

（2）对于第i台电动汽车，随机生成服从U（0,1）的随机数Rand，当Rand＞p时，电动汽车在行驶结束后进行充电，当Rand＞p时，电动汽车在不能满足行驶需求时进行充电。

2.2 充电需求计算方法

由于目前尚没有规模化的电动汽车运行，无法直接研究规模化电动汽车的充电负荷，因此大多数研究均是假设电动汽车的使用不改变用户的行驶规律，以传统燃油车的行驶规律概率特性为基础，采用蒙特卡洛模拟的方法计算得到充电负荷，计算方步骤如下：

（1）根据传统燃油汽车的行驶规律的概率分布，采用蒙特卡洛模拟技术得到数量为N的电动汽车用户的行驶里程、充电开始时间、和充电结束限制时间的随机数。

（2）设定电动汽车集群的充电概率为p，充电功率为Pc。

（3）模拟电动汽车行驶，更新动力电池荷电状态（State of Charge，SOC）。单台电动汽车行驶前后动力电池SOC的变化情况按照式（1）进行计算

式中，SOCi表示电动汽车动力电池的 SOC值；di和Di分别表示第i辆电动汽车的日行驶里程和续航里程；tti_1和tti_2分别表示电动汽车行驶起始和终止时间。

（4）生成随机数 Rand，判断动力电池剩余SOC，满足充电条件时，模拟电动汽车充电，得到各个时刻电动汽车的充电功率。单台电动汽车的充电功率可由表达式（2）表示，充电过程中电池SOC变化的过程可由表达式（3）计算

式中，pi(t)表示第i辆电动汽车在t时刻的充电功率；Pc表示恒定充电功率；tci_1和tci_2分别表示电动汽车充电起始和终止时间，并认为tti_2=tci_1；Ci表示第i台电动汽车的电池容量，kW·h。

（5）通过叠加得到规模化电动汽车的充电负荷P(t)，由表达式（4）计算。

3 不确定因素对充电负荷需求及配电网负荷影响

3.1 行驶规律特性及车辆参数

以北京市居民的行驶特性为依据，见表1所示，假设电动汽车的规模为500辆，考虑几种表2所示比较典型的车型参数，分析不确定充电概率、充电延时及充电功率对充电负荷需求和配电网负荷的影响，该城市典型负荷曲线如图1所示。

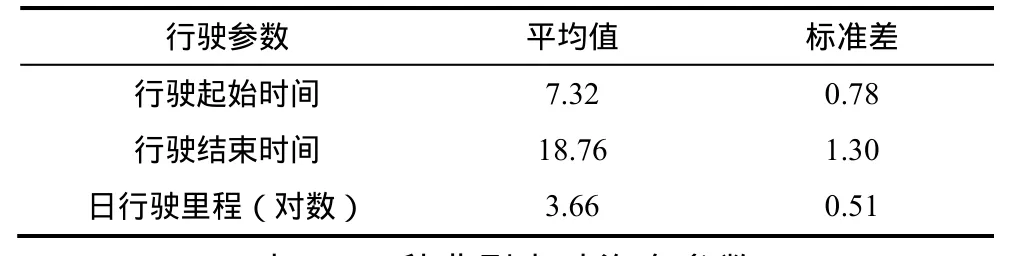
表1 用户行驶规律参数Tab.1 Parameters of the users’ drive habit

表2 5种典型电动汽车参数Tab.2 Parameters of five kinds classical EVs

图1 配电网负荷曲线Fig.1 Load profile of distribution power system

3.2 不确定充电习惯对充电需求的影响

假设电动汽车用户仅在居住地进行充电，按照表1所示的行驶特性数据，设充电功率Pc=3.3kW，计算出500辆电动汽车在不同充电概率情况下的充电需求曲线，如图2a所示，图中线下面积表示充电能量需求，可以验证不同充电概率时电动汽车集群充电能量需求基本相同。将充电需求叠加到电网负荷曲线上，得到不同集群充电概率下电网的负荷曲线，如图2b所示。

图2 不同充电概率时充电负荷需求和配电网负荷曲线Fig.2 Profiles of charging load demand and power load under different charging probabilities

从图2中可以看出，随着充电概率减小充电负荷需求曲线的峰值降低，而充电持续时间增长，同时对配电网负荷峰谷差的影响也降低；但是由于充电持续时间增长，充电负荷调节的时间裕度降低，不利于负荷调节，如果只追求配电网负荷的优化指标，可能会导致电动汽车用户充电能量需求得不到满足。

3.3 不确定充电起始时间对充电需求的影响

充电起始时间的不确定性也会引起充电负荷需求曲线的变化，和上述相同，假设充电概率p=0.5，充电功率Pc=3.3kW，通过仿真计算得到充电起始延时时间分别为 0h、0～2h和 0～4h三种情况下电动汽车集群的充电负荷需求曲线及对应的电网负荷曲线，如图3所示。

从图3中可以看出，随着充电起始时间延时的增大，电动汽车集群的充电负荷需求峰值减小，并且向后推移，对电网负荷峰谷差的影响也相应减小，因此可通过不同的充电起始时间延时进行充电负荷调节，而电动汽车的充电能量需求却可能受到影响。

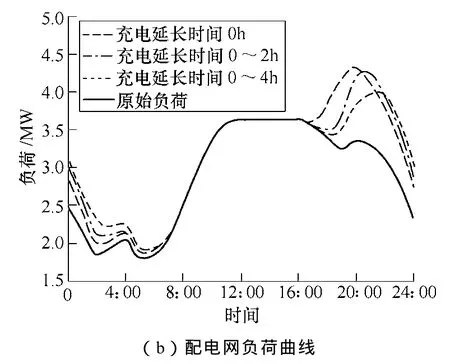
图3 不同充电延时时充电负荷需求和配电网负荷曲线Fig.3 Profiles of charging load demand and power load under different charging time delay

3.4 不确定充电功率对充电需求的影响

与上节相似，设定充电概率p=0.5，计算得到充电功率Pc分别为3.3kW、5.0kW和6.6kW三种情况下电动汽车集群的充电需求曲线，如图4a所示，以及含有充电负荷的电网负荷曲线，如图4b所示。

图4 不同充电功率时充电负荷需求和配电网负荷曲线Fig.4 Profiles of charging load demand and power load under different charging power

从图4中可以看出，随着充电功率增大，充电负荷需求的峰值及对配电网负荷峰谷差的影响均增大，然而相应充电持续时间的减小却有利于充电负荷的调节，与上述充电概率降低时充电负荷的变化恰好相反；因此，当充电概率比较小时，可通过增大充电功率进行充电负荷调节，在提高配电网负荷指标的同时也能满足电动汽车用户的充电需求。

4 充电负荷调节模型及求解

4.1 充电负荷调节模型

基于上述对充电习惯、充电延时和充电功率不确定性对充电需求的影响，在电动汽车充电习惯不确定的情况下，可通过充电延时和充电功率协调控制，在满足电动汽车充电能量需求和配电网运行约束的条件下，实现充电负荷的优化调节。对于充电负荷优化调节问题，一般以减小电网负荷方差、减小电网损耗或者提高电网负荷率为目标，文献[12]中论证了这三种目标具有等价性，因此，这里以电动汽车充电起始时间和充电功率为控制变量，以电网负荷方差最小为目标函数的优化模型。

目标函数为

式中，D(·)表示电网负荷方差；T表示电动汽车充电起始时间向量；pli表示第i时段配电网负荷；H表示负荷调节的时间段数量；pev_i表示电动汽车集群在第i时段的充电功率需求；Pav为含有充电负荷的平均电网负荷。

如上所述，充电负荷调节要在不影响用户充电能量需求的前提下进行，另外充电功率不能超过充电机的输出功率范围，因此，可建立如下约束条件。

（1）充电时间约束

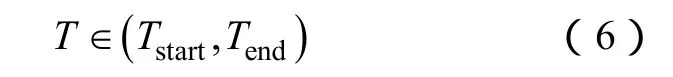
式中，Tstart、Tend是随机生成的两组数据，表示电动汽车能够充电的起始和终止时间向量，分别与行驶结束时间和行驶开始时间对应。

（2）充电功率约束

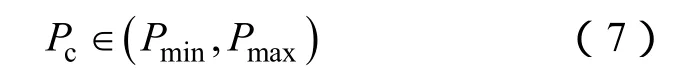
式中，Pmax和Pmin分别表示电动汽车充电机的最大、最小充电功率。

（3）充电能量需求约束

式中，xevi表示第i辆电动汽车充电能量满足状态，当满足时xevi=1，不满足时xevi=0；η表示电动汽车集群充电能量满足率。

4.2 优化模型最优解求解方法

由于上述优化模型的两个控制变量之间存在一定的相关性，即充电功率变化会引起充电延时范围（充电起始时间调节范围）的变化，因此属于动态规划问题。另外，考虑到目标函数的非线性、控制变量的解空间大等问题，这里选择粒子群优化算法（Particle Swarm Optimization, PSO）进行求解。对电动汽车充电起始时间构造种群规模为m的N维粒子XT，对充电功率构造一维粒子XP，分别称为时间粒子和功率粒子，其中第i个粒子如式（9）和式（10）所示。

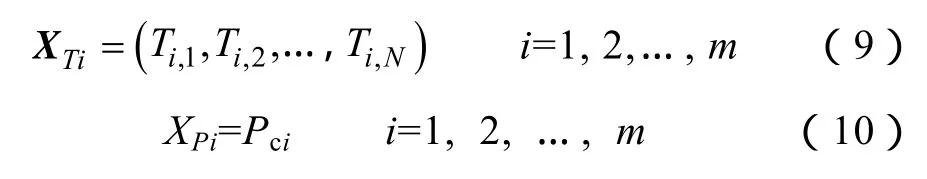
PSO的适应度函数由式（5）表示，粒子的更新采用表达式（11）和式（12）计算。

式中，ωmax、ωmin表示权重因子的最大、最小值；k表示当前迭代次数；K表示最大迭代次数。

由于充电功率和充电时长之间的相关性，在功率粒子更新后，时间粒子的最大值会发生变化，粒子群迭代过程中做如下处理

（1）更新计算充电时长

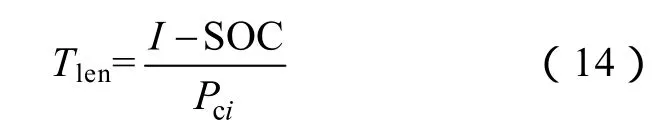
式中，Tlen表示电动汽车集群的充电时长向量；I表示SOC的充电目标值。

（2）更新充电调节时间范围

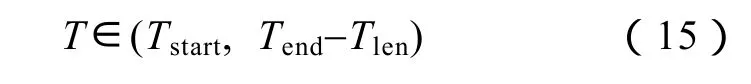
5 充电负荷调节仿真计算

5.1 PSO参数设置及收敛性分析

时间粒子的种群规模为m=20，粒子长度为电动汽车规模N=500，学习因子c1=c2=1.49，ωmax=0.95，ωmin=0.4，时间粒子速度的最大、最小分别为 5和-5，功率粒子速度分别为3和-3，负荷调节的时间段数H=240，最大迭代次数设定为300。

PSO计算时，迭代次数设置太小会导致收敛不到最优值，设置太大会导致计算时间过长，图 5所示是某一次计算时适应度值的收敛曲线，从图中可以看出，当粒子群迭代至200次时基本收敛到最优值。

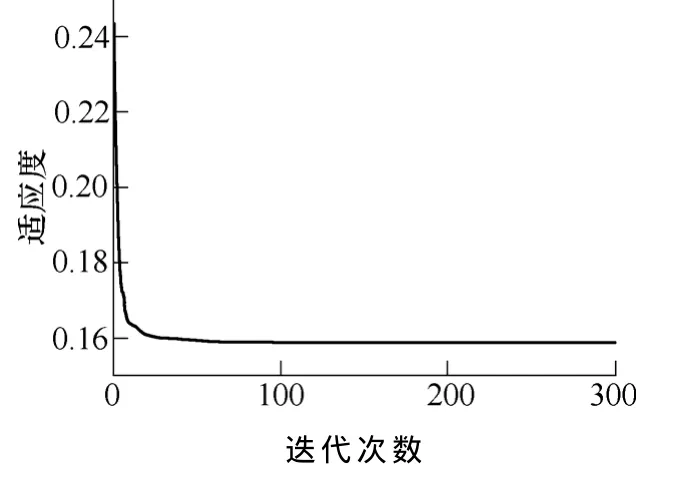
图5 PSO算法适应度值收敛曲线Fig.5 Convergence curve of PSO algorithm fitness value

5.2 电动汽车充电负荷调节

5.2.1充电负荷调节分析

按照上述参数求解充电负荷调节优化模型，设定功率粒子的最大、最小值为 6.6kW 和 3.3kW，N=500，得到充电起始时间调节和充电起始时间、充电功率同时调节两种优化模型的优化结果，如图6所示。图中为充电概率p=0.0时，按照两种调节方式的调节后的配电网负荷曲线。从图中可以看出，增加充电功率调节时，由于充电起始时间的调节范围变大，在 24时之前的充电功率降低，而在电网负荷低谷的地方却有相对较大的增长，也能更好地平滑原始负荷低谷期的波动，因此降低了电网负荷方差。

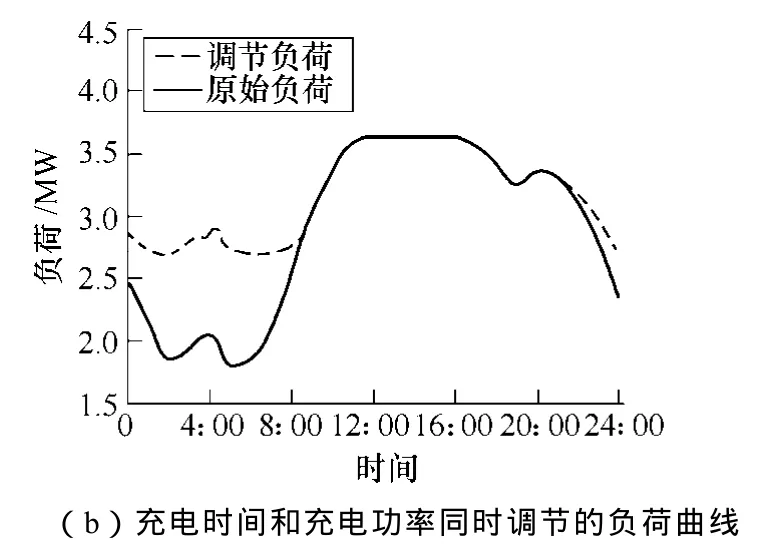
图6 充电负荷调节后的配电网负荷曲线Fig.6 Profiles of distribution power load after regulating

表3所示是在不同充电概率情况下，两种充电负荷调节的评价指标对比。从表中可以看出，当充电概率比较低时，仅仅采用充电起始时间控制（方法1），很难满足用户的充电能量需求，而增加充电功率调节（方法 2）后，提高了充电能量需求满足率指标，并且进一步减小了电网的负荷方差。由于电动汽车充电需求的随机性，每次计算的结果会有一定的差别，以下数据均为多次计算得到的平均值。

表3 充电负荷调节的评价指标Tab.3 Evaluation of the charging load regulation

5.2.2充电概率与最佳充电功率

按照第 3.4节中的分析，当充电概率减小时为了满足充电能量需求，需要适当提高电动汽车的充电功率，而充电功率过大又会引起负荷方差增大。这里以p=0.5，N=500为例，分析充电概率与充电功率之间的关系，计算得到图7所示曲线，从图中可以看出，在满足充电能量需求时需要进一步增加充电功率才能达到最小负荷方差，并定义负荷方差达到最小时对应的充电功率为最佳充电功率Pbest，p=0.5时的最佳充电功率为8.73kW。

图7 充电功率与充电能量需求满足率及负荷方差的关系Fig.7 Relationship among charging power, charging energy meet rate and load variance

表4所示为不同充电概率时的最佳充电功率。从表中可以看出，不同充电概率时最佳充电功率均不同，而最佳负荷方差基本相同，因此在进行充电负荷调节时需要根据不同的充电概率选择最优的充电功率。

5.2.3电动汽车集群规模与最佳充电功率

电动汽车的规模不同时，由于能够调节的充电能量需求不同，对应的最佳充电功率也会不同。表5所示为充电概率p=1.0，Pmax=20kW时，5种不同规模电动汽车集群的充电负荷调节数据，从表中可以看出，随着电动汽车规模增大，最佳充电功率会增加，对应最小负荷方差减小，因此，在不同规模电动汽车并入电网时，要选择合适的充电功率调节范围。

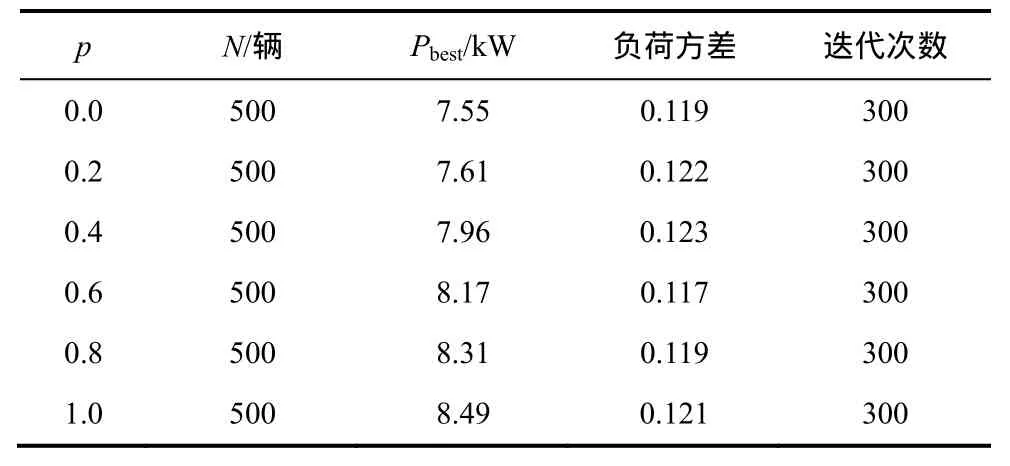
表4 充电概率与最佳充电功率关系Tab.4 Relationship between charging probabilities and charging power

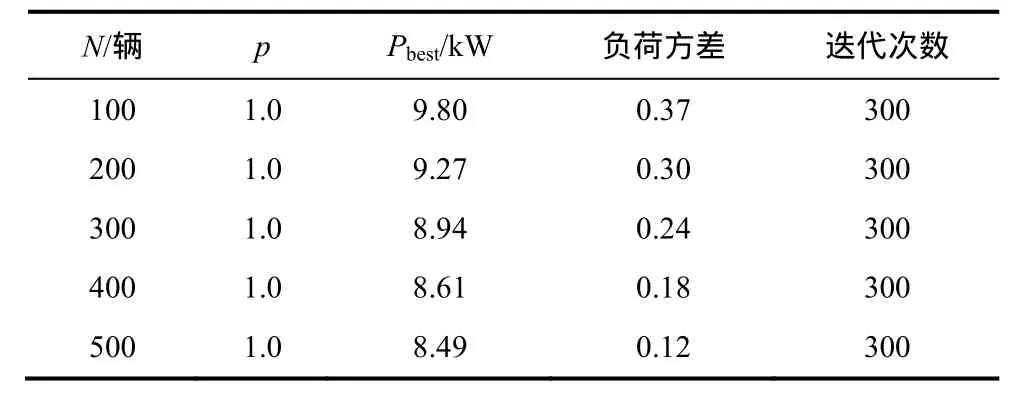
表5 电动汽车数量与最佳充电功率关系Tab.5 Relationship between EV’s number and charging power

6 结论

本文通过采用充电概率的方法对电动汽车不确定性充电习惯建模，分析了不同充电概率、不同充电延时和充电功率对充电负荷需求及其对配电网负荷的影响，研究发现通过采用充电延时和充电功率结合进行充电负荷调节能够在满足用户充电能量的前提下降低对电网的影响，因此提出了一种基于充电起始时间和充电功率控制的充电负荷调节策略，并构造双粒子群进行求解。通过仿真计算，验证了本文所提出的充电负荷调节策略的优越性。

[1] Robert C. Green, Wang Lingfeng, Mansoor Alam. The impact of plug-in hybrid electric vehicles on distribution networks: a review and outlook[J]. Renewable and Sustainable Energy Reviews. 2011, 1(15): 544-553.

[2] Hubner M, Zhao L, Mirbach T, et al. Impact of large-scale electric vehicle application on the power supply[C]. IEEE Electrical Power & Energy Conference,Montreal, 2009.

[3] Taylor J, Aaitra A, Alexander M, et al. Evaluation of the impact of plug-in electric vehicle loading on distribution system operations[C]. IEEE Power &Energy Society General Meeting, Calgary, Canada,2009.

[4] 胡泽春, 宋永华, 徐智威, 等. 电动汽车接入电网的影响与利用[J]. 中国电机工程学报, 2012, 32(4):1-11.

Hu Zechun, Song Yonghua, Xu Zhiwei, et al. Impacts and utilization of electric vehicles integration into power systems[J]. Proceedings of the CSEE, 2012,32(4): 1-11.

[5] Clement K, Haesen E, Driesen J. The impact of charging plug-in hybrid electric vehicles on a residential distribution grid[J]. IEEE Transactions on Power Systems, 2010, 25(1): 371-380.

[6] 罗卓伟, 胡泽春, 宋永华, 等. 电动汽车充电负荷计算方法[J]. 电力系统自动化, 2011, 35(14): 36-42.

Luo Zhuowei, Hu Zechun, Song Yonghua, et al. Study on plug-in electric vehicles charging load calculating[J]. Automation of Electric Power Systems, 2011,35(14): 36-42.

[7] 杨冰, 王丽芳, 廖承林. 大规模电动汽车充电需求及影响因素[J]. 电工技术学报, 2013, 28(2): 22-27.

Yang Bing, Wang Lifang, Liao Chenglin. Research on power charging demand of large-scale electric vehicles and its impacting factors[J]. Transactions of China Electrotechnical Society, 2013, 28(2): 22-27.

[8] Clement K, Haesen E, Driesen J. The impact of charging plug-in hybrid electric vehicles on a residential distribution grid [J]. IEEE Transactions on Power Systems, 2010, 25(1): 371-380.

[9] Qian Kejun, Zhou Chengke, Allan Malcolm, et al.Load model for prediction of electric vehicle charging demand[C]. IEEE International Conference on Power System Technology, Hangzhou, 2010.

[10] Acha S, Green T C, Shah N. Effects of optimized plug-in hybrid vehicle charging strategies on electric distribution network losses[C]. IEEE Transmission and Distribution Conference and Exposition, Los Angeles, 2010.

[11] Rotering N, Ilic M. Optimal charge control of plug-in hybrid electric vehicles in deregulated electricity markets [J]. IEEE Transactions on Power Systems,2011, 26 (3): 1021-1029.

[12] Sortomme Eric, Hindi Mohammad M, MacPherson S D James, et al. Coordinated charging of plug-in hybrid electric vehicles to minimize distribution system losses[J]. IEEE Transactions on Smart Grid, 2011, 2(1):198-205.

[13] Ikegami T, Ogimoto K, Yano H. et al. Balancing power supply-demand by controlled charging of numerous electric vehicles[C]. IEEE Electric Vehicle Conference, Singapore, 2012.

[14] Yano Hitoshi, Kudo Koji, Ikegami Takashi, et al. A novel charging-time control method for numerous EVs based on a period weighted prescheduling for power supply and demand balancing[C]. IEEE PES Innovative Smart Grid Technologies(ISGT), Washington,DC, 2012.

[15] Shrestha G B, Ang S G. A study of electric vehicle battery charging demand in the context of Singapore[C]. The 8th International Power Engineering Conference, 2007.