基于出行链的电动汽车充电负荷预测模型

陈丽丹 聂涌泉 钟 庆

（1. 华南理工大学电力学院 广州 510640 2. 华南理工大学广州学院电气工程学院 广州 510800 3. 香港理工大学电机工程学系 香港 999077）

1 引言

电动汽车是新能源汽车的主要发展方向，近年成为国内外汽车产业发展的热点，国家政策导向明显，发展速度日益加快，将逐步迈入产业化阶段[1]。但由于电动汽车用户需求和行为的不确定性与相互差异，未来大规模电动汽车充电负荷具有时间和空间上的随机性、间歇性和波动性等不确定特点[2,3]，将给电网的安全运行和优化调度带来困难[4,5]，要求建立有效的电动汽车充电负荷预测模型，为分析电动汽车充电负荷带来的影响和电动汽车广泛接入电网的调控策略制订打下基础，提供理论支持。

国内外针对电动汽车充电负荷建模研究主要集中在基于电动汽车使用出行需求的蒙特卡洛模拟法[6-9]，采用排队理论分析抵达充电站的电动汽车充电功率的概率分析方法[10,11]及物理分析法[12]。其中，文献[6]建立了电动汽车功率需求的统计学模型，用蒙特卡洛仿真方法求得单台电动汽车功率需求的期望和标准差，进而给出多台电动汽车总体功率需求的计算方法，考虑了充电起始时间和日行驶里程两个影响因素，但假设认为车辆最后一次返家时刻即为充电起始时间，这将充电频率限制在了一天一充模式，文献同时假设每百公里耗电量为固定值，然而电动汽车实际使用中一天可能会出现多次充电情况，电动汽车每百公里耗电也会随着气温、路况等因素发生变化，而非固定值。文献[7]针对公交车、公务车、出租车和家用车等四种电动汽车类型建立其充电负荷计算模型，但作者建模是以对各类型电动汽车设定固定的充电模式为前提，充电时间按车辆类型不同设定为服从均匀分布、直角梯形分布和正态分布等，其考虑的另一主要随机因素起始荷电状态（State Of Charge，SOC）同样基于主观假设为简单服从正态分布，这需要对电动汽车用户驾驶行为的进一步调研与深入分析。文献[8]假设日行程里程满足对数正态分布，并更为合理地给出了充电起始SOC的表达式，充电起始时间则结合英国通勤者与其他人士车辆用途不一设为服从均匀分布。文献[9]和文献[6]一样基于日行驶里程数据，但考虑不同电池容量类型的电动汽车，假设充电起始时间为车辆最后一次返家时刻，文中考虑了不同充电功率水平的充电负荷模型。文献[10,11]均以排队论为理论基础，假设电动汽车抵达充电站的时间服从泊松分布，其中前者从充电汽车电池的初始荷电状态和车辆到达充电站时间的随机分布为出发点，提出二阶段泊松分布电动汽车充电站集聚模型进行充电站集聚特性的模拟，将小区停车场视为一个充电站展开分析，而后者考虑的是高速公路路段进出车流量的统计，分析高速公路边充电站负荷，模型较为适用于集中停车场、充电站的负荷建模，对大量电动汽车接入配网充电进行整体分析时有一定局限性。文献[12]在探究大量电动汽车并网充电动态物理过程的基础上，通过建立描述该动态物理过程的数学方程来计算充电负荷，但作者对于电动汽车并网时的起始 SOC也仅是简单假设为服从正态分布。

总结上述文献在研究电动汽车充电负荷建模时只是简单给定了建模条件的电动汽车规模、起始SOC、起始充电时间和日行驶里程等几方面简单因素，与实际情况相差较大，研究大都忽视了充电负荷在时空上的随机性，对于电动汽车的出行分布预测、充电频率和充电场所多样性等方面考虑不够细致，预测方法还不成熟。

本文提出一种基于出行链的电动汽车负荷预测方法，能统筹兼顾电动汽车数量、电池容量、充电功率水平、充电频率、充电场所、起始荷电状态和起始充电时间等因素，给出电动汽车充电负荷的时间和空间分布。

2 基于出行链电动汽车充电负荷建模思路

由于家庭用汽车（简称私家车）运行方式比较随机、灵活，本文着重于私家电动汽车充电负荷的建模分析。另考虑到由于目前电动汽车处于试运行和逐步推广阶段，电动汽车用户出行特征相关的、可靠的历史数据较为缺乏，因此，本文假设电动汽车具有与传统燃油汽车相似的出行特征。

首先，按居民出行调查数据将车辆出行目的地充电场所分为五大类，采用三参数威布尔概率函数和对数正态概率函数拟合各段行程行驶结束时间和行驶距离。其次，基于家为起讫点以马尔科夫理论一次状态转移概率构建车辆出行简单链和复杂链模型。然后，考虑地区天气温度、交通路况对于电动汽车耗电量的影响，采用模糊算法计算车辆不同状况下每公里的耗电量。再根据是否充电的条件结合不同充电场所的充电功率水平计算出充电持续时间，建立充电负荷预测模型，使用蒙特卡洛方法模拟各类型出行链电动汽车的行程结束时间、行驶距离和充电等，最终得到不同场所的电动汽车充电负荷的时间分布。本文预测电动汽车充电负荷的整体建模思路如图1所示。

3 车辆出行时空模型

3.1 行程结束时间和行驶距离

根据我国传统居民出行调查一般将出行目的分为上班、上学、公务、购物、文娱体育、探亲访友、看病、回程和其他九大类[13]。按国外活动类型的归类，将上述出行目的分为五大类：回家（Home，H）、工作（Work，W）、购物吃饭（Shopping& Eating，SE）、社交休闲（Social& Recreational，SR）和其他事务（Other Family/Personal Errands，O）。

图1 建模思路Fig.1 Overview of proposed model

在一个区域内，车辆可以认为在这五大类行程目的地之间行驶，充电行为可能发生在这五大目的地，其每段行程结束的时间和行驶距离是随机的。

（1）行程结束时间分布。因为威布尔（Weibull）函数[14]拟合随机数据时有很大的灵活性和适应性，本文采用式（1）描述的三参数Weibull概率函数对每段行程结束时间进行拟合，即

式中，x为随机变量，k为形状参数，c为尺度参数，γ为位置参数。k、c两个参数控制Weibull分布曲线的形状，k表示分布曲线的峰值情况，无量纲；c与行程结束时间的平均值有关，min。

（2）行程行驶距离分布。对美国家庭交通出行调查数据（NHTS）[15]进行统计，每段行程行驶里程d可近似为对数正态分布，其概率密度函数为

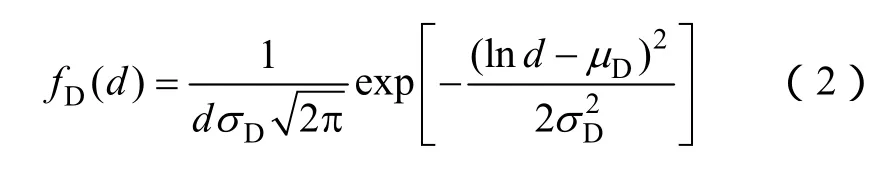
式中，μD为行程行驶距离期望值；σD为标准差，km。

（3）拟合效果检验。为检验每段行程结束时间和行驶距离的拟合效果，本文采用 Kolmogorov-Smirnov（K-S）检验方法[16]，即

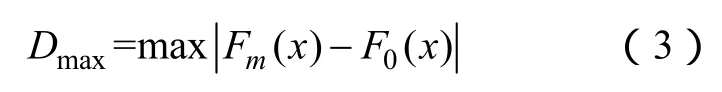
式中，Fm(x)代表实际观察到m个随机样本在变量x上的累积概率；而F0(x)表示预先假设的理论分布（如上述 Weibull分布、对数正态分布）的累积概率；Dmax表示两者间的差距大小绝对值中的最大值。当Dmax＜Dα时，即Dmax小于显著性水平下的临界值Dα时，就认为样本数据服从假设的 Weibull分布，其中Dα为 K-S检验显著性水平临界值，可查文献[17]中临界值表获得，本文α默认为0.05，则Dα=1.36，m为样本大小。

3.2 出行链结构

为分析私家车辆一天中行程时空分布情况，本文以家为车辆一天往返行程的起讫点；其次，根据文献[15]数据统计，私家车平均出行链长度 3.02，行程大于3的出行链大部分是因中途含有接送某人时等短暂停留的行程，如上班途中送孩子上学，送达学校时的停留。在行程链中这些极短暂的停留目的地视为不可能充电是合理的。故本文忽略次要的出行目的，考虑最长含3个行驶目的地的主要出行链结构，其结构可分为两种模式：①活动目的单一的出行链（称为简单链），共4种，如图2a所示；②多种类型的活动构成复杂出行链（称为复杂链），共12种，如图2b所示。

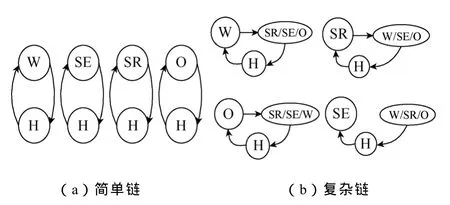
图2 基于家为起讫点的典型出行链结构Fig.2 The typical structure of trip chains based on home

3.3 车辆时空分布

3.3.1车辆空间转移概率

马尔科夫过程[18]是用于描述具有无后效性的随机过程：若每次状态的转移只与前一时刻的状态有关而与过去的状态无关，离散马尔科夫过程称为马尔科夫链。记当前时刻的状态为Ei，下一时刻的状态为Ej，则马尔科夫链可用条件概率表示

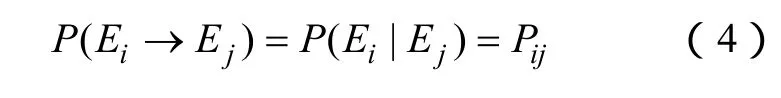
若将每个行驶目的地视为一个状态，根据马尔科夫理论，车辆下一个状态（目的地）即由当前状态决定。记pij为从状态Ei转为状态Ej的状态转移概率，则其一步状态转移概率可写成矩阵形式为

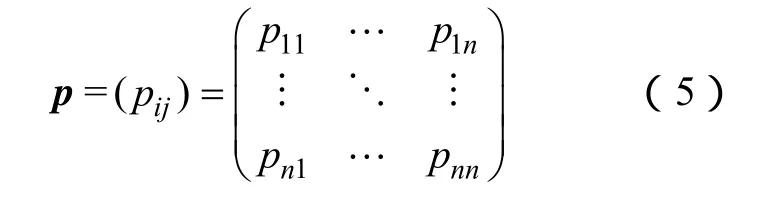
假定车辆目前处于E1，那么在下一时刻，它可能由状态E1转向E1,E2,… ,En中的任一个状态。所以pij满足条件

针对本文研究的5大场所（H、W、SE、SR和O），即可能状态E1,E2, … ,E5，上述式（5）和式（6）只需将n改为 5，即表示电动汽车从一个目的地行驶到另一个目的地的一步转移概率为

式中，pij可根据当地居民出行调研数据统计确定。

3.3.2行程结束时间关系

图2a所示的简单链的结构中，车辆出行途中仅有一个停留可能充电地点，其起始充电时间（行程结束时间）可由 Weibull分布函数直接拟合得到。但对于图2b中所示的复杂链结构，两段行程结束时间之间存在一定关系和约束，此处采用线性相关系数[19]分析，即

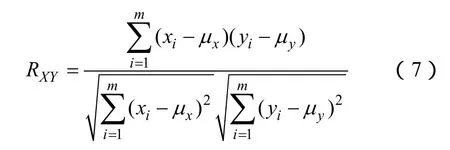
式中，RXY表示相关系数，xi、yi为行程结束时间矩阵X、Y中的元素，μx、μy为两段行程结束时间X、Y的平均值，m为样本大小。

当RXY≥0.7时，认为X、Y存在较强的线性关系，两者之间可由关系可表示为

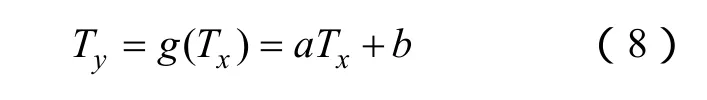
式中，Tx、Ty分别表示两段行程结束的时间，以一天1 440min表示；a、b为线性系数。

当RXY＜0.7时，两段行程结束时间线性关系不强，此种情况下，由 Weibull三参数的调整来描述各个行程结束时间的约束关系为

其中

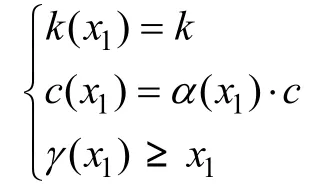
即当前行程结束时间的分布曲线形状k不变，和原来相同；尺度参数c根据上一行程结束时间做相应修正，1()xα为(0,1)之间的随机数；位置参数大于上一行程结束时间，即当前行程结束的时间不能早于上一程的结束时间。

仿真计算时，针对简单链行程，两段行程结束时间由各自的Weibull分布函数抽取；针对复杂链，若其中两段行程存在较强线性关系，则先抽取前一行程结束时间，再由式（8）确定当前行程结束时间；若线性关系不强，则当前行程结束时间的 Weibull分布参数通过式（9）进行调整后再抽取确定。

4 电动汽车充电负荷计算

4.1 每公里耗电量

电动汽车充电负荷与其每公里耗电量ω相关，文献[6]视其为固定值，这对预测结果带来一定误差。每公里耗电量ω的精确获得是极其困难的，其值一般在 0.15～0.30kW·h/km，具体受电池使用年限、交通路况、温度和电池能量管理系统效率等因素影响[20]。本文计算ω时重点考虑交通路况和温度这两个随机因素[21,22]，因无法用准确的数学表达式表示，本文采用模糊数学理论进行计算。首先，将一天当中各时刻的交通路况从顺畅到拥堵归一化到[0,1]，以三角形状呈现；其次，天气过冷、过热时需要开起空调，此处将温度归一化为

式中，Zt为归一化后的温度，无量纲；zt为实时温度；zmin为最低温度；zmax为最高温度，℃；p为比例系数；Matlab/Simulink模糊计算的过程如图 3所示。

图3 每公里耗电量模糊计算过程Fig.3 Fuzzy calculating process of power consumption per km

4.2 车辆充电频率

现有文献考虑较多的为一天一充[6]，或是设定固定的充电模式[5,7]。但用户行驶到某个目的地时是否会充电往往取决于电动汽车电池现有剩余电量是否足以完成下一段行程的行驶，另为确保安全还需考虑30%的剩余电量[23]，本文假设电动汽车行驶到目的地n时的充电条件如下

式中，Sn为车辆抵达目的地n时的电池荷电状态；C为电池容量，kW·h；ωn为行驶至n的车辆每公里耗电量；ln表示行驶至n行程的行驶距离；n+1为下一行程。

式（11）、式（12）表示车辆行驶至n时，判断电池剩余电量，若不能满足在抵达n+1时电池将仍有不少于30%的余量，则在n地需充电，反之不充。

4.3 车辆充电时长

电动汽车充电持续时间由电池容量、起始荷电状态和充电功率水平等因素共同决定。车辆若需在目的地n充电，则其充电时长可估计为

4.4 充电负荷计算及仿真流程

基于上述方法可获得每辆电动汽车的行驶时空分布、充电等情况，进而可以得到其在每个目的地的充电负荷。采用蒙特卡洛模拟方法计算电动汽车充电负荷，其仿真计算流程如图4所示。

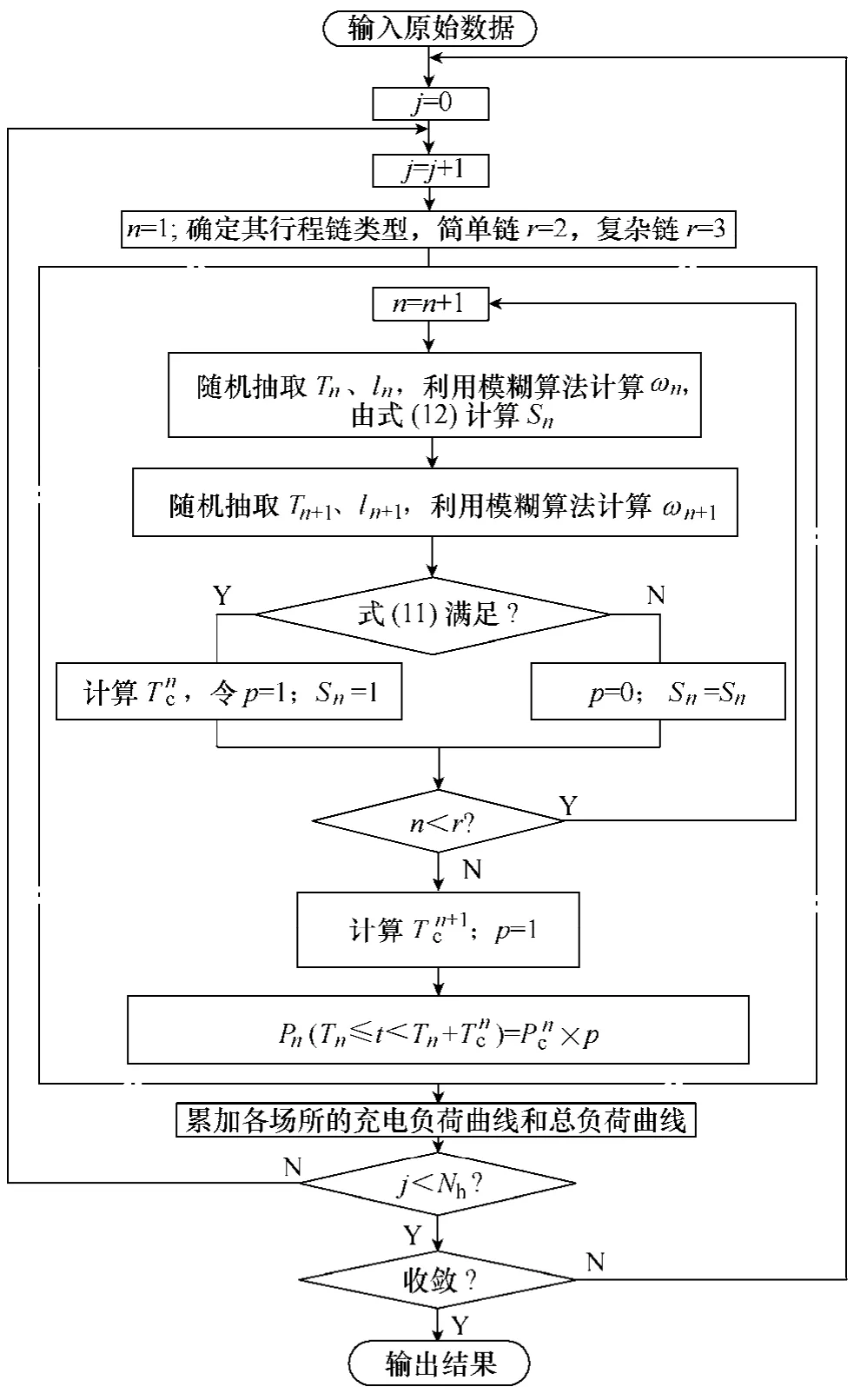
图4 基于Monte Carlo模拟的充电负荷计算流程图Fig.4 Flow chart of charging power calculating based on Monte Carlo simulation

系统的输入信息包括：①电动汽车总数量，及该区域每类行程链的比例；②车辆电池容量，每个目的地场所的充电功率水平、充电效率；③各类行程链每一行程的起始充电时间和行驶距离的概率分布；④一天当中的气温数据、交通路况数据；⑤起始值：n=1 ，S1=1；⑥仿真次数。

当车辆j抵达某个目的地n时，由式（12）计算得到此地此时的剩余电量，并由式（11）判断它是否满足下一程的行驶要求。若需充电，简单行程链的充电起始时间由式（1）概率函数的抽取确定，复杂链的充电起始时间由式（1）、式（8）和式（9）共同确定，充电时长由式（13）计算。第k辆电动汽车在n处t时刻充电的概率可表示为

式中，Ty为行驶至目的地n时的行程结束时间，为车辆在n处的充电时长。由此，将各个场所每一辆电动汽车充电负荷曲线累加，得到各场所电动汽车一天的充电功率

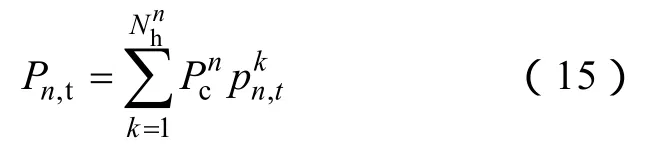
5 仿真结果与分析

5.1 居民出行调研数据

国内外居民出行调查统计数据经过多年调查和积累已较为完善，本文采用较有代表性的NHTS2009[15]，该调查由美国交通部于2008～2009年期间完成，其中 DAYV2PUB.xls数据库为本文算例分析数据来源，该数据库有65 536条行程，记录了被调研家庭ID号，家庭成员ID号，车辆ID号，以及一天当中每一行程的起始、结束时间和每一行程的行驶距离，以及每一行程的目的和行驶日期等信息。

5.2 行程结束时间

5.2.1单个行程结束时间

图5所示为统计NHTS2009数据中W-H、H-SE行程的结束时间概率分布，可以看出单个行程的结束时间并非服从如文献[6,7]所述正态或均匀分布。

图5 单个行程结束时间分布Fig.5 End time distribution of single trip

本文采用式（1）对图5中W-H行程结束时间进行拟合，得到 Weibull三参数为(k,c,γ)=(3.10,420,671)；而 H-SE行程结束时间 Weibull概率拟合分布三参数为(k,c,γ)=( 1.85,341,414)。明显地，W-H行程形状系数k比后者 H-SE行程大得多，前者因与工作相关，上、下班时间一般有约束，后者 H-SE行程表示人们由家出行前去购物吃饭等活动，出行时间相对自由，故其行程结束时间分布比较分散。

5.2.2行程链中行程结束时间关系

按图2出行链结构，根据习惯大部分私家车用户选择在抵达家里或是其他停车场（位）开始充电，其每段行程结束时间：①简单链：以 H-W-H和H-SR-H为例，它们两段行程结束时间的概率分布分别如图6所示；②复杂链：以H-SE-W-H、H-WO-H、H-O-SE-H和H-SR-SE-H为例，其三段行程结束时间的概率统计分布如图7所示。

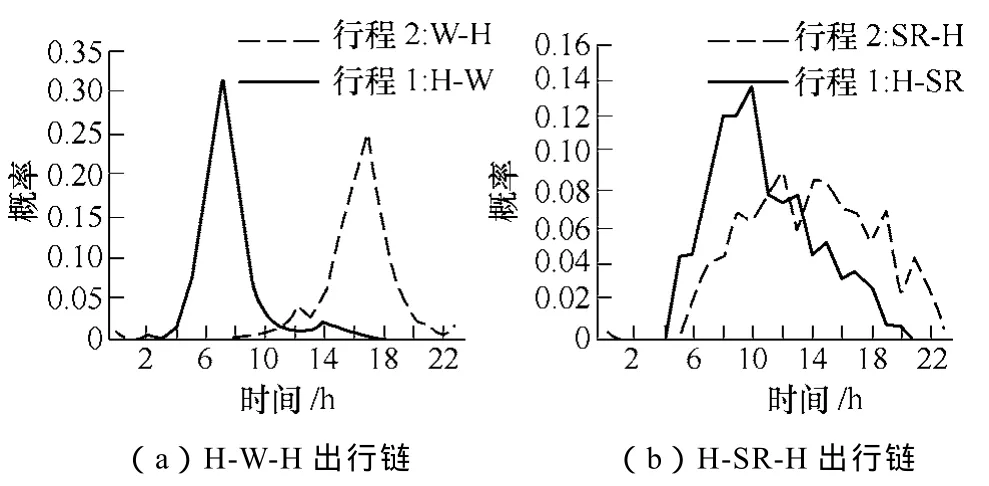
图6 简单链行程结束时间分布Fig.6 End time distribution of simple trip chains

图7 复杂链行程结束时间分布Fig.7 End time distribution of complex trip chains

由图 6、图7可以看出，与工作相关的行程结束时间分布比较集中，早上在8点左右，下午在17点左右。其余行程结束时间则相对分散。采用式（7）分析图7a所示的H-SE-W-H复杂链各段行程结束时间的线性关系，其值为

由式（16）中 (1,2)0.88=R可知，在H-SE-W-H复杂出行链中，第2段行程SE-W和第1段行程HSE的结束时间线性关系较强，表明人们在上班 W前还进行了 SE活动，且若其出行时间早，则抵达上班单位时间也早，反之亦然。两段行程结束时间的线性关系表示为

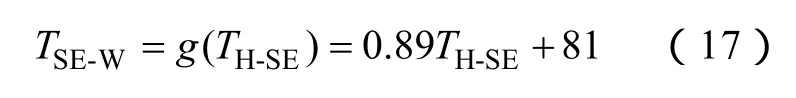
对此类复杂链，仿真时先抽取第1段行程H-SE的结束时间和行驶距离，并判断 SE处是否充电；第2段行程SE-W结束时间由式（17）确定，抽取第2段行驶距离，判断W处是否充电；第3段行程W-H结束时间单独抽取。

图7b所示H-W-O-H复杂链三段行程结束时间的线性关系不强，其值为

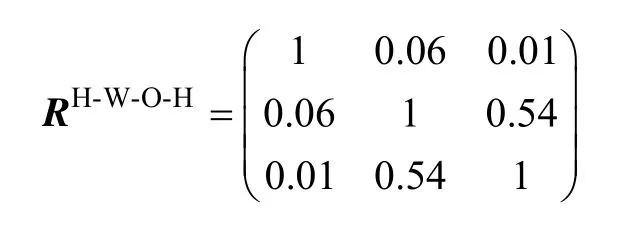
该情况下，仿真时先抽取第1段行程结束时间TH-W，再抽取第2段行程结束时间TW-O，第3段的行程结束时间TO-H抽取前先对其Weibull三参数进行修正，其中分布曲线形状k不变，尺度参数修正为c'=rand(1)c；位置参数修正为γ=TW-SR，如此确保抽取的第3段行程结束的时间不早于第2段行程的结束时间。

5.3 行程行驶距离

以NHTS2009统计H-W行程为例，图8所示为其行驶里程的概率分布。

图8 H-W行程行驶里程概率分布Fig.8 Driving distance distribution of H-W trip

其行驶里程满足对数正态分布，采用式（2）拟合得：μD=2 .78，σD=0 .82，km；其余行程行驶里程同样可采用对数正态分布拟合得到。

5.4 每公里耗电量计算结果

以 Nissan Leaf电动汽车为例，其电池容量为24kW·h，续航里程在正常气候条件、工况下为160km[23]。但交通、天气状况不同时，续航里程也随之发生变化，见表1所示[24]。

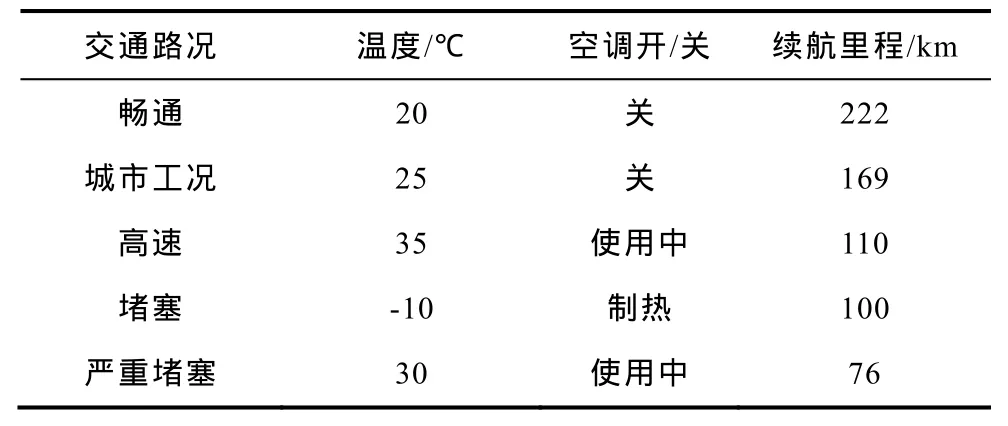
表1 不同工况下测试续航里程数Tab.1 Tested maximum range under different conditions

由表1可得，Nissan Leaf在五种不同状况下的续航里程从76～222km不等，表明不同交通路况、温度对电动汽车耗电量有较大影响。由本文 4.1节所述模糊数学方法，采用的模糊规则由表1五种方案产生，每公里耗电量的计算结果如图9所示。

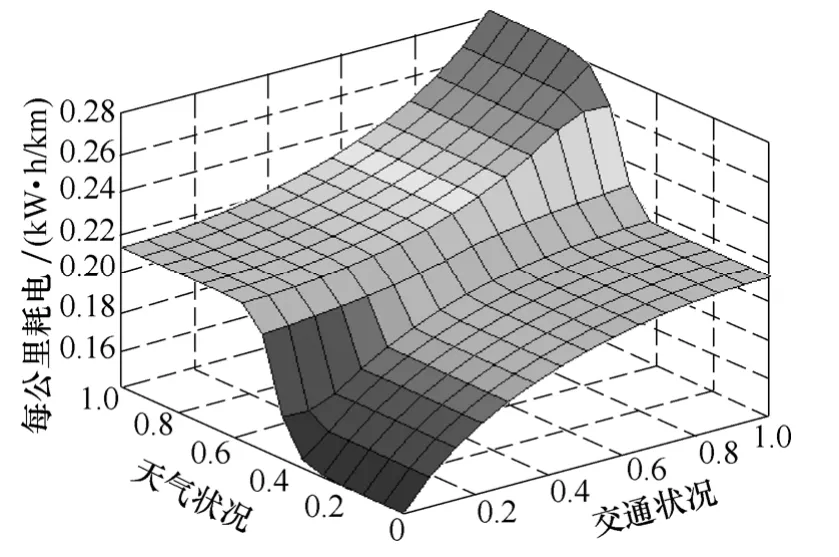
图9 每公里耗电量模糊计算结果Fig.9 The result of energy consumption per km based on fuzzy computing method

5.5 电动汽车充电负荷预测结果

5.5.1仿真参数

考虑Nissan Leaf，家和其他公共场所的充电功率水平根据 SAE J1772标准分别设定为 3.3kW，19.2kW[25]。车辆数参考某市截至2012年5月汽车保有量数据240.5万量的0.1%取整设为2 400辆，以代表某一区域的车辆保有量。区域原始负荷曲线如附图1所示。

由NHTS2009统计分析，选取其中主要含有的出行链来说明本文所建模型和求解方法，各出行链夏冬季、工作日和周末的占比见附表1。算例系统输入的夏、冬季天气温度和交通路况数据见附表2。系统蒙特卡洛仿真次数设为1 000次。

5.5.2仿真结果

（1）情形1：不同渗透率下电动汽车充电负荷

以电动汽车占汽车保有量的比例为渗透率，分析夏季工作日情景下当渗透率变化时充电负荷期望值情况如图10a所示，图10b所示则为该情景模式下电动汽车渗透率变化时充电负荷对原有负荷曲线的影响。

图10 夏季工作日不同渗透率下负荷曲线Fig.10 The load curve of different penetrations under summer work day situation

（2）情形2：夏冬季工作日与周末充电负荷

夏冬季、工作日和周末等不同情景模式下的电动汽车总充电期望负荷曲线如图11所示。

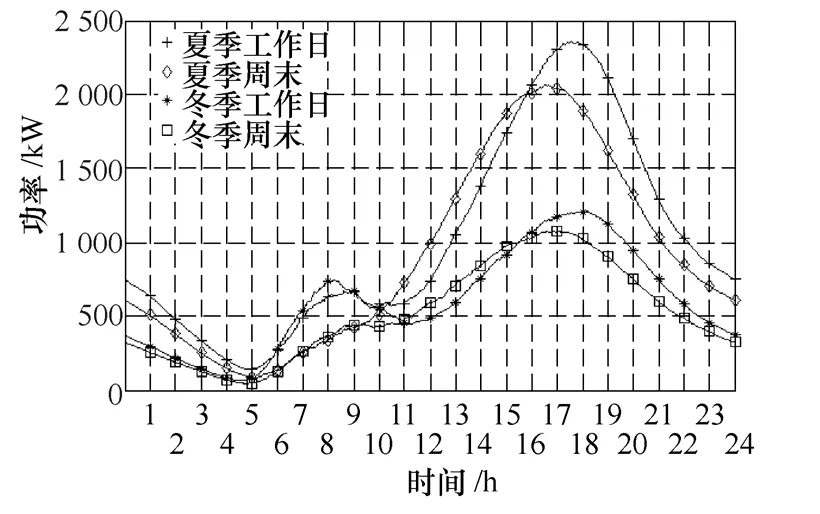
图11 不同情景模式下的电动汽车充电负荷期望Fig.11 The expected charging load of EVs under different conditions

（3）情形3：各场所夏冬季工作日与周末充电负荷

夏冬季工作日与周末H、W、SE、SR、O 5个场所一天内充电期望负荷曲线如图12所示。

图12 5个场所电动汽车充电负荷预测曲线Fig.12 The charging load curves of EVs in five locations

（4）情形4：改变每公里耗电量时充电负荷

本文建模考虑温度、交通路况对电动汽车行驶耗电量的影响，此处在夏季工作日情景下，分别计算了每公里耗电量设为固定值w=0.21kW·h/km和变化时的电动汽车充电负荷对比曲线，如图13所示。从图中可看出，当温度和交通状况如附表1中变化时，w随之变化引起的晚高峰时段充电负荷值较当w设为固定值时大。

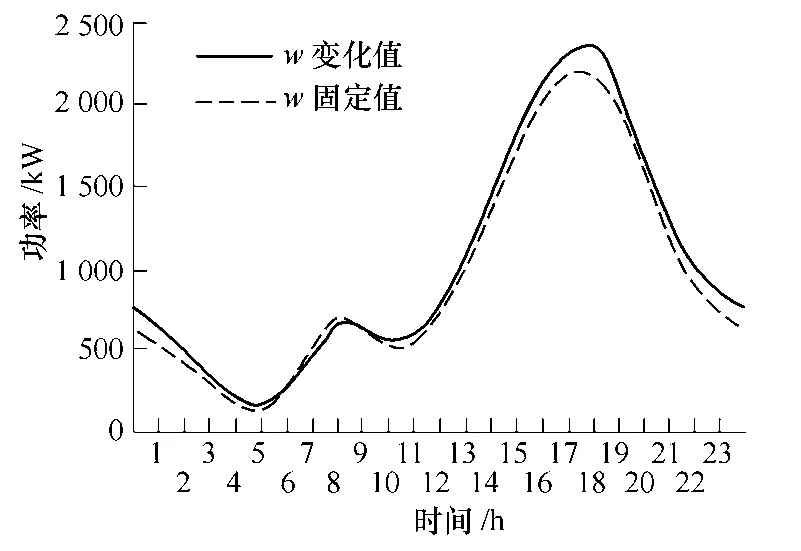
图13 改变每公里耗电量电动汽车充电负荷Fig.13 The charging load when power consumption changes

（5）情形5：与其他方法预测结果的对比

设电动汽车规模同样为 2 400辆，恒充电功率水平3.3kW，一天一充模式，参考文献[6]方法，起始充电时间设服从正态分布（1 7.6,3 .42），日行驶里程服从对数正态分布μD=3 .2，σD=0 .88，每公里耗电量设为固定值w=0.21kW·h/km；参考文献[7]方法，设30%的电动汽车选择在办公地点充电，起始充电时间满足正态分布（9，0. 52），70%电动汽车选择返家后充电，起始充电时间满足正态分布(19,1.52)，起始SOC服从正态分布NSOC（0.6，0.12）分布，采用蒙特卡洛方法计算充电负荷期望，曲线如图14所示。计算各方法日均充电电量，结果如表2所示。

图14 电动汽车充电负荷曲线Fig.14 The charging load curves of EVs

表2 各方法计算结果表Tab.2 Calculating results of different methods

5.5.3结果分析

（1）电动汽车充电负荷具有明显峰谷差，随着电动汽车渗透率提高，整体负荷也逐步加大。

（2）充电负荷具有季节特性，夏季整体充电负荷比冬季大，这是由于人们出行发生变化，冬季简单链比例增加，日平均行驶里程减少，充电负荷随之降低；因周末上班人数少，含工作出行链比例降低，周末的充电负荷相对工作日较低；周末人们返家时刻提前，周末的充电负荷高峰时刻比工作日提前约1h。

（3）由图12反映出各个充电场所在夏冬季、工作日和周末的充电负荷变化情况，可知周末各场所充电负荷相对平时有所降低；居住区配电系统承担最多充电负荷，其他场所充电负荷较居住区相对分散。

（4）电动汽车耗电量w受天气温度、交通路况等影响，从而影响电动汽车充电负荷大小变化。

（5）因本文方法考虑充电场所多样性、一天多充可能性，计算所得的负荷曲线较为平坦，而其他文献方法采用一天一充频率，导致负荷高峰基本集中在车辆结束一天行程返家时刻附近；由本文方法计算得到的日均充电电量与所参考文献方法计算结果接近。

6 结论

电动汽车是未来的发展方向，也是智能电网的重要组成部分，电动汽车充电负荷预测是分析电动汽车与配电系统交互关系、制定协调控制策略的研究基础，其困难在于预测建模因素的随机性、不确定性。本文结合居民出行调研数据，建立了每公里耗电量变化、考虑充电频率、基于出行链结构的电动汽车充电负荷预测模型，具有通用性，适用于地区配网分析。

[1] 中华人民共和国科技部. 电动汽车科技发展“十二五”专项规划[EBOL].[2012-08-07]. http://www.gov.cn/zwgk/2012-04/20/content2118595.

[2] Wu Di, Aliprantis D C, Gkritza K. Electric energy and power consumption by light-duty plug-in electric vehicles[J]. IEEE Transactions on Power Systems,2011, 26(2): 738-746.

[3] Santos A, McGuckin N, Nakamoto H Y, et al.Summary of travel trends: 2009 national household travel survey[R]. 2011.

[4] 高赐威, 张亮. 电动汽车充电对电网影响的综述[J].电网技术, 2011, 32(2): 127-131.

Gao Ciwei, Zhang Liang. A survey of influence of electric vehicle charging on power grid[J]. Power System Technology, 2011, 35(2): 127-131.

[5] Pieltain Ferna X, Ndez L, Go X, et al. Assessment of the impact of plug-in electric vehicles on distribution networks[J]. IEEE Transactions on Power Systems,2011, 26(1): 206-213.

[6] 田立亭, 史双龙, 贾卓, 等. 电动汽车充电需求的统计学建模方法[J]. 电网技术, 2010, 34(11): 126-130.

Tian Liting, Shi Shuanglong, Jia Zhuo. A statistical model for charging power demand of electric vehicles[J]. Power System Technology, 2010, 34(11): 126-130.

[7] 罗卓伟, 胡泽春, 宋永华, 等. 电动汽车充电负荷计算方法[J]. 电力系统自动化, 2011, 35(14): 36-43.

Luo Zhuowei, Hu Zechun, Song Yonghua, et al. Study on plug-in electric vehicles charging load calculating[J]. Automation of Electric Power Systems, 2011,35(14): 36-42.

[8] Qian Kejun, Zhou Chengke, Allan M, et al. Modeling of load demand due to EV battery charging in distribution systems[J]. IEEE Transactions on Power Systems,2011, 26(2): 802-810.

[9] Darabi Z, Ferdowsi M. Aggregated impact of plug-in hybrid electric vehicles on electricity demand profile[J]. IEEE Transactions on Sustainable Energy, 2011,2(4): 501-508.

[10] 郑竞宏, 戴梦婷, 张曼, 等. 住宅区式电动汽车充电站负荷集聚特性及其建模[J]. 中国电机工程学报,2012, 32(22): 32-38.

Zheng Jinghong, Dai Mengting, Zhang Man, et al.Load cluster characteristic and modeling of EV charge station in residential district[J]. Proceedings of the CSEE, 2012, 32(22): 32-38.

[11] Sungwoo Bae, Alexis Kwasinski. Spatial and temporal model of electric vehicle charging demand[J]. IEEE Transactions on Smart Grid, 2012, 3(1): 394-403.

[12] 刘鹏, 刘瑞叶, 白雪峰, 等. 基于扩散理论的电动汽车充电负荷模型[J]. 电力自动化设备, 2012,32(9): 30-34.

Liu Peng, Liu Ruiye, Bai Xuefeng, et al. Charging load model based on diffusion theory for electric vehicles[J]. Electric Power Automation Equipment,2012, 32(9): 30-34.

[13] 杨敏. 基于活动的出行链特征与出行需求分析方法研究[D]. 南京: 东南大学, 2007.

[14] 胡恩平, 罗兴柏, 刘国庆. 三参数Weibull分布几种常用的参数估计方法[J]. 沈阳工业学院学报, 2000,19(3): 89-93.

Hu Enping, Luo Xingbobai, Liu Guoqing. Parameter estimating methods for the three parameters Weibull distribution[J]. Journal of Shenyang University of Technology, 2000, 19(3): 89-93.

[15] U.S. Department of transportation, federal highway administration, 2009 national household travel survey[DB/OL]. URL: http://nhts.ornl.gov.

[16] Frank J, Massey Jr. The kolmogorov-smirnov test for goodness of fit[J]. Journal of the American Statistical Association, 1951, 46(253): 68-78.

[17] Agostino R B D, Stephens M A. Goodness of Fit Techniques[M]. Boca Raton, FL, USA: CRC Press,1986.

[18] Grahn P, Munkhammar J, Widen J, et al. PHEV home charging model based on residential activity patterns[J]. IEEE Transactions on Power Systems, 2013, 28(3):2507-2515.

[19] Alicja L, Dorota K, Georgios P, et al. Stochastic modeling of power demand due to EVs using copula[J]. IEEE Transactions on Power Systems, 2012, 27(4):1960-1968.

[20] Rautiainen A, Repo S, Järventausta P, et al. Statistical charging load modeling of PHEVs in electricity distribution networks using national travel survey data[J]. IEEE Transactions on Smart Grid, 2012, 3(4):1650-1659.

[21] Shaaban M F, Atwa Y M, Saadany E F El. PEVs modeling and impacts mitigation in distribution networks[J]. IEEE Transactions on Power Systems,2011, 28(2): 1122-1131.

[22] Boriboonsomsin K, Barth M. Impacts of road grade on fuel consumption and carbon dioxide emissions evidenced by use of advanced navigation systems[J].Transportation Research Record, 2011, 2139.

[23] http://www. nissanusa. com/electric-cars/leaf/.

[24] Urban dynamometer driving schedule(UDDS) [OL].Available: www.epa.gov.

[25] Yilmaz M, Krein P T. Review of battery charger topologies, charging power levels, and infrastructure for plug-In electric and hybrid vehicles[J]. IEEE Transactions on Power Electronics, 2013, 28(5): 2151-2169.