恢复潮流可行的交直流电力系统切负荷新模型

聂永辉 杜正春 李崇涛 李天云

（1. 东北电力大学教务处 吉林 132012 2. 西安交通大学电气工程学院 西安 710049 3. 东北电力大学电气工程学院 吉林 132012）

1 引言

由于系统的故障使得系统潮流可解域大大收缩，从而导致潮流无解，进一步导致系统失去稳定或电压崩溃， 因此不考虑变压器抽头以及电容器投切等慢动态元件对恢复潮流解的作用，主要采取切负荷措施尽快恢复系统的潮流解，这就是恢复潮流解的控制问题；如果系统在恢复潮流解之后存在越限情况，则需要采取有效措施将系统的平衡点调整到可行域之内，采取的控制措施包括负荷切除、发电机有功出力调整、补偿电容器、调节有载调压变压器抽头等，这就是恢复可行解的控制问题[1-3]。

目前，对电力系统恢复潮流解和可行解问题的研究主要集中在交流系统。针对潮流无解的故障,文献[3]把参数空间中无解的点与最临近可解域边界上点的距离的计算转化为一类非线性优化问题,从而确定了恢复潮流解的最小负荷切除量；文献[4]为恢复故障后的潮流可解性，提出了一种快速恢复潮流解的切负荷算法，进而利用基于灵敏度的线性优化消除恢复潮流解后的系统越限现象，若恢复潮流解后系统不存在越限现象则通过扩展潮流方程减少切负荷量；文献[5]采用内点法解决恢复潮流解问题；文献[6]采用恢复潮流解和恢复可行解的两步法,以最小控制代价为目标, 把恢复系统可行解的控制问题转化为一类非线性规划问题求解，并考虑采用离散变量的原对偶内点法求解。可以看出，利用优化方法对于恢复潮流可行解问题是一定重要手段，如何把优化方法扩展到交直流混合系统的恢复潮流可行解问题，对于电力工作者来说是一个有意义的课题。

目前，非线性预测-校正原对偶内点法（Predictor-Corrector Primal-Dual Interior Point Method，PCPDIPM）因具有计算的数值稳定性和快速的收敛特性等优点而被认为是求解大规模 OPF问题较有效的方法[7-15]。该算法在优化过程中需要计算模型中各个函数对应的海森矩阵，但对于现有的优化模型，其各个函数是优化变量的高阶函数，因此各个函数对应的海森矩阵不是常数，这就需要在优化计算中对其不断进行更新，为此增加了优化总时间。因此如何把高阶优化模型转变成二阶模型，提高优化速度，对内点法来说是一个有意义的课题。文献[11]在直角坐标系中建立了基于非线性内点法的最优潮流问题，但由于有载调压支路模型中电流比变量的存在，该构建格式并不完全是二次的；文献[12]通过在有载调压支路模型中引进虚拟节点，由此在直角坐标系中建立了无功优化问题的二次新模型，模型中各个函数对应的海森矩阵在迭代过程中只需要计算一次，从而减少优化时间，但那只应用于交流系统；文献[16]提出了基于极坐标系的交直流混合系统优化模型，但模型中各个函数对应的海森矩阵随着迭代的进行而变化，这就需要在优化计算中对其不断进行更新，为此增加了优化总时间。

基于上述分析，针对潮流恢复的后一问题，本文通过在交流侧有载可调变压器支路模型中引入虚拟节点，并通过该节点的电压变量来表示有载可调变压器支路功率方程，使其不含有变压器电流比这个变量；对于直流系统，在换流变压器的理想变压器和换流阻抗之间引进一个虚拟节点，虚拟节点电压幅值等一些变量被用来表示换流器支路方程；在此基础上引进切负荷量，由此建立了交直流混合系统恢复潮流可行性问题的二次切负荷新模型。该模型的海森矩阵在迭代过程中是恒常矩阵，只需要计算一次，这样减少了内点法的计算机消耗总时间。

2 交直流系统二次潮流可行性恢复新模型

对于交流侧电力系统，有载调压变压器支路可由理想变压器串联导纳支路组成，如图1所示。其中，i和j分别是有载调压变压器的标准侧节点和非标准侧节点，t为LTC电流比，yt=gt+ jbt是LTC导纳，Vi=ei+ jfi和Vj=ej+jfj是标准侧和非标准侧节点电压，STij=PTij+jQTij和STji=PTji+ jQTji是标准侧和非标准侧节点注入功率。

图1 变压器等效模型Fig.1 Transformer equivalent model

直角坐标系的好处是可以建立二次函数，但由于LTC电流比的存在，导致有载调压变压器支路功率均是电流比和电压的高次函数，其对应的海森矩阵不是常数，因此在基于预测-校正原对偶内点的优化计算中，每次迭代时都需要计算，这增加了整个优化时间。为此，文献[12]在理想变压器和串联导纳之间引进一个虚拟节点，如图1所示，由于理想变压器是无损耗的，则有载调压变压器支路功率方程可表示为[12]

由于理想变压器是无损的，则其两侧电压应满足下列关系

由上可知，通过引进虚拟节点，方程式（1）～（6）是节点电压和变压器电流比的二次函数。

对于和交流节点i(i=1 ,… ,nd)相连的换流器，如图2所示，采用标幺值表示时[17-19]，其平均直流电压为

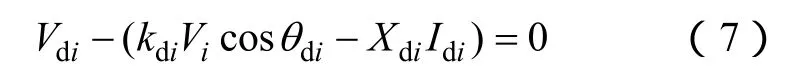
式中，Vi为交流节点i的电压幅值，当交流侧采用直角坐标系时，Vi可表示为，Vdi、Idi、Xdi、kdi、θdi分别是直流电压、直流电压、换流电抗、换流变压器电流比，换流器控制角；nd为换流器个数。

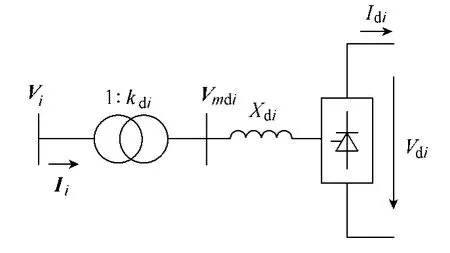
图2 换流器等效模型Fig.2 Converter equivalent model

假设换流器是无损耗的，平均直流电压还可以表示为

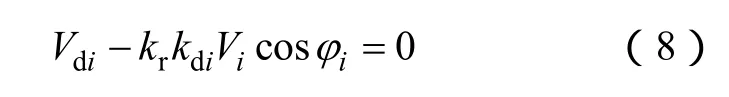
式中，φi为换流器的功率因数角。

忽略换流器的损耗，换流器的有功功率为

换流器从交流侧吸收的无功功率为

式中，φi为功率因数角。

由上述可知，式（7）～式（10）是变量的高阶函数。为了把它们变成二次方程，首先对与换流器相连的交流节点i引入其电压幅值Vi作为直流侧变量；接着引入与换流器相连的交流节点i相对应的电流幅值Ii和其实部、虚部作为直流侧变量（见图2）。其次不直接用θdi而用其余弦 cosθdi作为直流侧变量；最后在换流变压器的换流阻抗和理想变压器之间引入一个虚拟节点，其节点电压幅值变量Vmdi也作为直流侧变量。经过上述处理，可以在极坐标系下建立直流系统的方程，直流系统的方程只与电压幅值变量和电流幅值变量有关，而与相角无关。则上述方程可写成

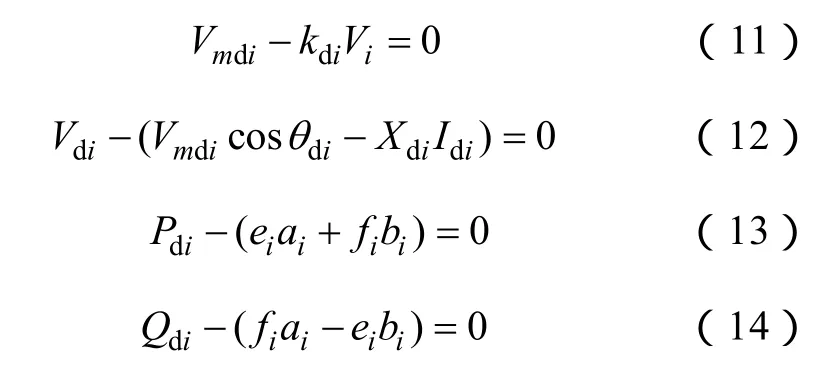
忽略换流器的损耗，直流功率等于交流基波的有功功率

交流电流基波分量的有效值和直流电流的关系为

直流网络方程为

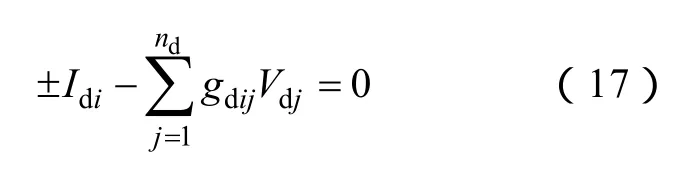
换流器一般有定电压、定电流、定功率、定控制角和定换流变压器电流比五种基本控制方式，其控制方式必须根据交直流混合系统的实际运行需要加以指定。整流器按定功率或定电流控制方式运行；逆变器按照定电压或定控制角控制方式运行，简写为

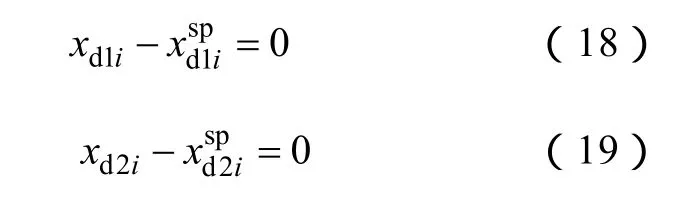
式中，xd1i、xd2i代表直流电压、直流电流、直流功率、换流器变压器电流比和控制角的余弦等变量之一。

引入的电压幅值变量和注入电流幅值变量是极坐标系下的变量，而它们的实部和虚部是直角坐标系下的变量，通过下列关系，把基于直角坐标系下的交流侧方程和基于极坐标系下的直流侧方程耦合到一起，形成一个统一交直流混合系统模型。

可以看出，经过上述处理，直流侧方程式（11）～式（19）和耦合方程式（20）、式（21）都是二次函数。

当节点电压和直流输电能力等限制引起交直流电力系统潮流不可行时，引进切负荷量来恢复潮流可解。按照引入电流ai+ jbi的参考方向，对于节点i(i=1 ,… ,nB)，考虑切负荷量的节点交直流电力系统功率平衡方程为

式中，Ci是节点i的有功切负荷量，按等功率因数削减无功负荷；λ是为了增加负荷水平；SLi为与节点i相连的一般支路集合；STi与节点i相连的有载调压支路集合；nB为系统原有的节点数；Gij和Bij是不包括有载调压支路而形成的导纳矩阵的第i行第j列元素的实部和虚部；PGi和QGi为节点i的发电机有功出力和无功出力；PLi和QLi为节点i的有功负荷和无功负荷；QCi为节点i的并联无功补偿出力；PTij和QTij为LTC支路的有功功率和无功功率，如果节点i为非标准侧节点，PTij和QTij的计算公式为式（1）和式（2），如果节点i为标准侧节点，PTij和QTij的计算公式为式（3）和式（4）。

基于以上推导的LTC支路二次模型、直流系统二次模型、二次坐标耦合方程、交直流混合系统的二次节点切负荷功率平衡方程，本文以各个节点（包括虚拟节点）的实部、虚部、发电机有功出力，发电机无功出力、并联无功补偿出力、有载调压电流比、节点切负荷量作为交流侧优化变量；以和换流器有关的虚拟节点电压幅值、节点电压幅值、电流幅值、电流实部、电流虚部、直流电压、直流电流、换流器控制角的余弦和换流变压器电流比作为直流侧优化变量，以节点切负荷量加权和最小为目标函数，建立以下的二次交直流混合系统的潮流可行解恢复模型。

本文以节点切负荷量加权和最小为目标函数，可表示为

等式约束包括交流 LTC电压转换方程式（5）和式（6）；直流方程式（11）和式（12），式（15）～（19）；坐标耦合方程式（20）和式（21），交直流混合系统的节点切负荷功率平衡方程等。交直流混合系统的节点功率平衡方程是把式（13）和式（14）代入式（22）和式（23）后，消去变量Pdi和Qdi而形成的。

不等式约束包括节点电压幅值、发电机有功出力、发电机无功出力、并联无功补偿出力、切负荷量、LTC电流比、支路传输功率、直流电压、直流电流、直流功率、换流器吸收的无功功率、换流器控制角的余弦和换流变压器电流比等上下限约束，它们表示为

不管是整流器还是逆变器，都从交流系统吸收无功功率，按照图2所示的电流方向，无功功率应大于零；但整流器从交流系统吸收有功功率应大于零，逆变器向交流系统注入有功功率应小于零。

由上可见，所建优化模型是优化变量的二次函数，因此，各个函数的海森矩阵都是恒常矩阵，在PCPDIPM 的整个优化过程中只计算一次，从而加速了整个优化过程；但由于优化变量和等式约束个数的增加，使修正方程的阶数增加，从而增加了修正方程的求解时间。但利用列近似最小度法（Column Approximate Minimum Degree, COLAMD）有效缓解这个问题，和传统模型相比，本文所提模型在形成系数矩阵时所节省的时间大于求解修正方程的增加时间，这在后面的仿真计算将被证实（关于PCPDIPM的介绍详见文献[7-15]，这里将不再赘述）。

3 算例仿真

本文在硬件为奔腾2.1（2GB内存），操作系统为Windows XP环境下，采用Matlab7语言进行编程仿真校验，采用标幺值和平启动方式计算。对于4个测试系统，直流电压的范围取为0.9～1.1(pu)，直流电流的范围取为 0.5～2(pu)；控制角范围取为15°～25°，整流变压器的电流比的范围取为 0.85～1.15(pu)，等效换相电阻取为 0.039(pu)，直流线路电阻0.013(pu)。测试系统情况如下[20]：

（1）系统 1：在 IEEE 14系统中，节点 2和 4之间的交流输电线被直流输电线替代，修改之后的IEEE 14系统是一个包含二端直流输电网络的交直流混合电力系统。

（2）系统2：在IEEE 30系统中，节点2、4、6之间的3条交流输电线被直流输电线替代，修改之后的IEEE 30系统是一个包含三端直流输电网络的交直流混合电力系统。

（3）系统 3：在 IEEE 57系统中，节点 8和 9之间的交流输电线被直流输电线替代，修改之后的IEEE 57系统是一个包含两端直流输电网络的交直流混合电力系统。

（4）系统4：在IEEE 118系统中，节点26、30之间和节点80、77之间的两条交流输电线被直流输电线替代，修改之后的 IEEE 118系统是一个包含两条输电网络的交直流混合电力系统。

表 1所示为新模型（M1）与传统模型（M2）在一次迭代时形成修正方程系数矩阵和求解修正方程所需要的时间、迭代总时间和迭代次数。可以看出，新模型在一次迭代时形成系数矩阵所需要的时间比常规模型少，这是由于所建模型是二次模型，其目标函数，等式约束和不等式约束相对应的各个海森矩阵是恒常矩阵，在整个迭代过程中只需要计算一次，这减少了形成系数矩阵所需要的时间；对于传统模型，由于交流LTC和直流系统的影响，其模型是高阶函数，对应的各个海森矩阵在每一次迭代过程中都需要更新，因此增加了形成修正方程系数矩阵所需要的时间。但在求解修正方程时，新模型所需要的时间比常规模型有所增加，这是因为该模型引入一些优化变量，导致等式约束和拉格朗日乘子均有所增加，从而增加了牛顿方程的阶数，但nT和nd远远小于系统节点数和支路数，利用COLAMD算法有效地减少求解新模型牛顿方程所增加的时间。仿真计算得出，新模型形成修正方程系数矩阵所节省的时间大于求解修正方程所增加的时间，从而使新模型所需要的优化总时间比传统模型少，系统规模愈大，节省的时间愈多。

表1 优化结果比较Tab.1 Optimal comparison between two models

表2所示为电压幅值在不同约束情况下，经本文的恢复潮流可行新模型对IEEE 14交直流系统所计算的优化结果。当电压幅值限制在0.94～1.06(pu)和 0.98～1.02(pu)时，原问题不需要切负荷，经其他控制手段优化后潮流可行，由于限制比较宽松，所以迭代7次和8次就可以收敛；当电压幅值限制在0.99～1.01(pu)和0.995～1.005(pu)时，原问题潮流不可行，需要分别切除负荷0.047 9(pu)和0.167 6(pu)才能使恢复潮流可行，由于限制比较严，所以迭代27次和30次才可以收敛，另外，在这两种情况下，切负荷位置分别是14和12～14节点，这说明这些节点是负荷端，缺少无功电源支撑，所以这些节点容易越下限，只有切除这些节点的部分负荷才能维持电压幅值在所要求的区间内。

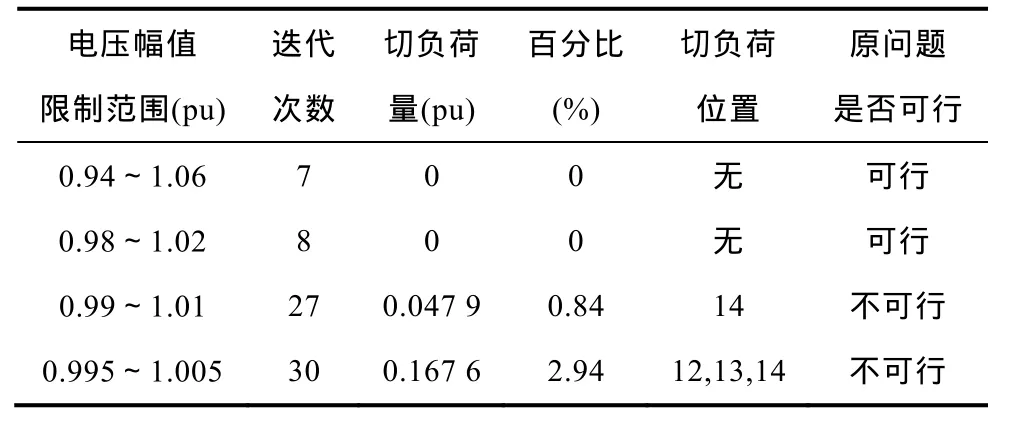
表2 考虑电压约束的优化结果Tab.2 Optimal results considering voltage constraints

表3和表4显示了直流线路电流在不同约束情况下，经本文的恢复潮流可行新模型对 IEEE 14交直流系统所计算的优化结果。当直流电流限制在0.8(pu)和0.6(pu)时，原问题不需要切负荷，经其他控制手段优化后潮流可行，迭代14次和17次就可以收敛；当直流电流限制在 0.4(pu)和 0.3(pu)时，原问题潮流不可行，需要分别切除负荷0.051 1(pu)和0.116 2(pu)才能恢复潮流，由于限制比较严，所以迭代55次和56次才可以收敛，另外，在这两种情况下，切负荷位置分别是10、6、10、14节点。表4显示了直流线路电流在不同约束情况下，经本文的恢复潮流新模型优化后，交流线路 2-3，3-4和4-5所传输电流和功率的优化结果（参考方向从小号节点指向大号节点），随着直流线路电流约束限制的增强，从节点5流向节点4和从节点2流向节点3的电流和有功功率增加，来满足节点3有功负荷需要（该节点所接负荷为总负荷的 16.53%），而从节点4流向节点3的电流和有功功率逐渐减少，这是直流线路输电能力受到约束的结果。

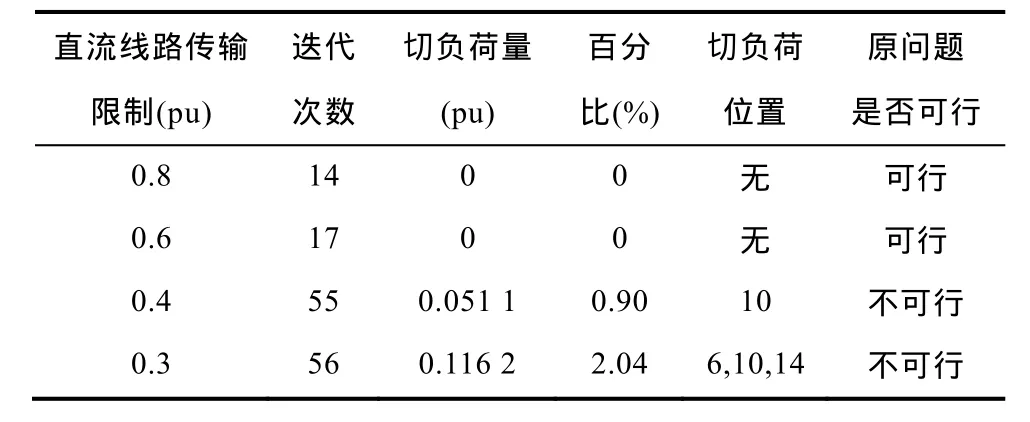
表3 考虑直流线路传输约束的优化结果Tab.3 Optimal results considering DC line transmission constraints

表4 考虑直流线路传输约束的优化结果Tab.4 Optimal results considering DC line transmission constraints

表5所示为交流线路5-4在不同电流幅值约束情况下，经本文的恢复潮流新模型对 IEEE14交直流系统所计算的优化结果。当交流电流幅值限制在0.8(pu)和0.6(pu)时，原问题不需要切负荷，经其他控制手段优化后潮流可行，由于限制比较宽松，所以迭代14次和17次就可以收敛；当电流幅值限制在 0.3(pu)和 0.245(pu)时，原问题潮流不可行，需要分别迭代51次和98次，切除负荷0.430 8(pu)和0.585 8(pu)才能恢复潮流，切负荷位置分别是2、3、6、13和2、3、6、10-14节点，在这种情况下切负荷位置为电源侧和负荷侧，这是由于无功传输的路径受到限制，只有切除电源侧和负荷侧节点所接的部分负荷，才能维持这些节点电压要求，而前面直流线路受到约束限制时，切负荷位置却为负荷侧，无功传输的路径未受到限制，所以无功电源供应比较充足的电源侧节点所接负荷并未切除，只切除无功电源比较缺乏的负荷侧部分负荷，来满足电压约束要求。

表5 考虑交流线路4-5传输约束的优化结果Tab.5 Optimal results considering AC line 4-5 transmission constraints

4 结论

本文通过对有载调压变压器支路和换流器支路的有效处理，引进切负荷量，由此建立了交直流混合系统恢复潮流可行性问题的二次切负荷新模型。当最小切负荷为零时，说明原系统利用其他控制手段就可以恢复潮流可行，当最小切负荷不为零时，说明原系统必须利用最小切负荷等控制手段才能恢复潮流可行，这说明最小切负荷量可以作为测量电力系统不可行程度的一种手段。预测-校正原对偶内点法被用来实现这个最优潮流问题，该模型的海森矩阵是恒常矩阵，在整个优化过程中只需要计算一次，这样减少了内点法的计算机消耗时间；利用COLAMD算法对牛顿方程的系数矩阵进行节点优化排序，以降低求解修正方程所需要的时间。仿真计算结果验证了所建模型正确性和有效性。

[1] 余贻鑫, 李鹏. 基于混合法的潮流可行域边界计算[J]. 电力系统自动化, 2004, 28(13): 18-24.

Yu Yixin, Li Peng. Computing the boundary of the power flow feasible region based on the hybrid method[J]. Automation of Electric Power Systems, 2004,28(13): 18-24.

[2] 余贻鑫, 李鹏, 孙强, 等. 电力系统潮流可行域边界拓扑性质及边界算法[J]. 电力系统自动化, 2006,30(10): 6-11.

Yu Yixin, Li Peng, Sun Qiang, et al. Study on topological properties of boundary of power flow feasibility region and algorithm for boundary computation[J]. Automation of Electric Power Systems, 2006,30(10): 6-11.

[3] Thomas J Overbye. A power flow measurement for unsolvable cases[J]. IEEE Transactions on Power Systems, 1994, 9(3): 1359-1365.

[4] 傅旭, 王锡凡. 静态安全分析中的联动切负荷算法[J]. 中国电机工程学报, 2006, 26(9): 82-86.

Fu Xu, Wang Xifan. New approach to load-shedding in static state security analysis of power systems[J].Proceedings of the CSEE, 2006, 26(9): 82-86.

[5] Granville S, Mello J C O, Melo A C G. Application of interior point methods to power flow unsolvability[J].IEEE Transactions on Power System, 1996, 11(2):1096- 1103.

[6] 郭力, 张尧, 胡金磊, 等. 恢复潮流可行解的优化控制策略[J]. 电力系统自动化, 2007, 31(16): 24-28.

Guo Li, Zhang Yao, Hu Jinlei, et al. An optimal control strategy for recovering feasible solution of the power flow[J]. Automation of Electric Power Systems,2007, 31(16): 24-28.

[7] 姚煜, 蔡燕春. 离散粒子群与内点法结合的电力系统无功优化[J]. 电力系统保护与控制, 2010, 38(3):48-52.

Yao Yu, Cai Yanchun. A hybrid strategy based on DPSO and IPM for optimal reactive power flow[J].Power System Protection and Control, 2010, 38(3):48-52.

[8] 程军照, 李澍森, 程强. 一种无功优化预测校正内点算法[J]. 电工技术学报, 2010, 25(2): 152-157.

Cheng Junzhao, Li Shusen, Cheng Qiang. A predictorcorrector interior point method for optimal reactive power[J]. Transactions of China Electrotechnical Society, 2010, 25(2): 152-157.

[9] 熊宁, 张魏, 黄金海, 等. 基于约束松弛变量策略的中心校正内点法[J]. 电力系统保护与控制, 2012,40(14): 20-25.

Xiong Ning, Zhang Wei, Huang Jinhai, et al. Centrality correction interior point method based on constrained slack variables strategy[J]. Power System Protection and Control, 2012, 40(14): 20-25.

[10] 邸弢, 李华强, 范锫. 基于奇异值分解和内点法的交直流系统无功优化[J]. 电工技术学报, 2009,24(2): 158-163.

Di Tao, Li Huaqiang, Fan Pei. Reactive power optimization of AC/DC power system based on singular value decomposition and interior point method[J].Transactions of China Electrotechnical Society, 2009,24(2): 158-163.

[11] Torres G L, Quintana V H. An interior-point method for nonlinear optimal power flow using voltage rectangular coordinates[J]. IEEE Transactions on Power System, 1998, 13(4): 1211-1218.

[12] 余娟, 颜伟, 徐国禹, 等. 基于预测-校正原对偶内点法的无功优化新模型[J]. 中国电机工程学报,2005, 25(11): 146-151.

Yu Juan, Yan Wei, Xu Guoyu, et al. A new model of reactive optimization based on predictor corrector primal dual interior point method[J]. Proceedings of the CSEE, 2005, 25(11): 146-151.

[13] 刘沛津, 谷立臣, 韩行. 基于内点法与改进遗传法的无功规划优化混合算法[J]. 电力系统保护与控制,2008, 36(17): 56-59.

Liu Peijin, Gu Lichen, Han Xing. Reactive power planning based on IPM and improved GA hybrid method[J]. Power System Protection and Control,2008, 36(17): 56-59.

[14] 简金宝, 杨林峰, 全然. 基于改进多中心校正解耦内点法的动态最优潮流并行算法[J]. 电工技术学报,2012, 27(6): 232-241.

Jian Jinbao, Yang Linfeng, Quan Ran. Parallel algorithm of dynamic optimal power flow based on improved multiple centrality corrections decoupling interior point method[J]. Transactions of China Electrotechnical Society, 2012, 27(6): 232-241.

[15] Granville S. Optimal reactive dispatch through interior point methods[J]. IEEE Transactions on Power System,1994, 9(1): 136-146.

[16] Lu C N, Chen S S, Ong C M. The incorporation of HVDC equations in optimal power flow methods using sequential quadratic programming techniques[J]. IEEE Transactions on Power System, 1988, 3(3): 1005-1011.

[17] 李兴源. 高压直流输电系统[M]. 北京: 科学出版社, 2010.

[18] 王锡凡, 方万良, 杜正春. 现代电力系统分析[M].北京: 科学出版社, 2007.

[19] 赵畹君. 高压直流输电工程技术[M]. 北京: 中国电力出版社, 2009.

[20] Yu J, Yan W, Li W Y, et al. Quadratic models of AC–DC power flow and optimal reactive power flow with HVDC and UPFC controls[J]. Electric Power Systems Research, 2008, 78(3): 302-310.