空空导弹侧向射流与气动舵协调控制技术

张公平，段朝阳，2，廖志忠

(1.中国空空导弹研究院，河南 洛阳 471009;2.航空制导武器航空科技重点实验室，河南 洛阳 471009)

0 引 言

侧向反作用射流控制技术在防空/反导导弹领域得到了成功应用。例如，法国的Aster15/30 防空导弹、俄罗斯的9M96E/E2 防空导弹，以及美国的PAC－3 导弹［1－2］。而在空空导弹领域，尚未有该技术成功应用的先例。

随着军事科技的不断进步，战场环境日益复杂。空空导弹的作战对象已不再局限于常规飞机，而需要面对包括隐身飞机、无人机、巡航导弹，甚至是地面防空雷达与弹道导弹等新型威胁，这就要求未来空空导弹采用新型控制技术。

早在1992年，美国McDonald Douglas 公司就开始研究“可替代控制技术”，即反作用射流控制技术。1997年，项目内容扩展，并更名为“空中优势导弹技术”项目。2003年，项目内容继续扩展，从而成为Boeing 公司“双任务空中优势导弹”项目［3］。此外，美国Lockheed Martin 公司也曾计划实施“空射撞击杀伤”项目，实际上就是改进PAC－3导弹，开发空射版，以期拦截弹道导弹与巡航导弹［4］。直到最近，该公司公开Cuda 导弹项目，仍将反作用射流列为优势技术。此外，欧洲MBDA 公司的CAMM 防空导弹，也采用反作用射流技术，并提出了空射版升级计划［5］。

可见，反作用射流控制技术是发达国家为夺取制空权而优先资助的一项关键技术，近年来已逐渐成为一个新的研究热点。但相关研究多集中于可滚转弹体的一次性射流控制理论层面，而对复杂度更高，适用范围更广的可重复性射流控制技术，则少有涉及。

［6］中的弹体模型，深入研究可重复性侧向射流与气动舵的协调控制方法。通过引入射流脉冲等冲量调制技术，构建适于LTI 控制器设计的连续系统模型。并基于Fourier 级数理论，分析弹体对高频射流信号的低通滤波特性，揭示离散脉冲对弹体姿态的连续操纵机理。然后，利用线性二次型技术，为导弹设计最优控制律，并联合有效集算法，对控制量进行二次动态分配，从而实现复合控制系统的综合优化。

1 具有多操纵机构的导弹动态建模

根据小扰动线化理论及通道分离原理，可将导弹非线性系统分别解耦为俯仰、偏航、横滚等三通道动态模型:

其中:Tx，Ty，Tz为产生三通道操纵力矩的离散式侧喷直接力，因此，该模型实质上是一个混杂系统。ld，ly，lz为三通道侧喷直接力的力臂。其他符号定义见文献［6］。

2 高频射流的动态建模与控制

目前，直接针对混杂系统的控制器设计难度较大，可将其转化为连续系统设计问题。首先研究离散脉冲信号经射流装置执行后对弹体的操纵响应。理想信号采用方波脉冲，实际信号以延迟时间表征射流装置的动态特性。

2.1 离散脉冲的Fourier 级数理论

射流装置延迟时间为滞后时间与斜边时间的总和。滞后时间是指从指令信号发出时刻到射流装置开始执行时刻的迟滞时间;而斜边时间指的是从射流装置开始执行时刻算起，到首次达到幅值的迟滞时间，如图1 所示。

图1 侧向射流装置响应过程示意图

图1 中，T 为脉冲周期;ta为指令信号起始时刻;tb为脉冲宽度;τ0为滞后时间;τ 为斜边时间。在一个脉冲周期内，响应过程可用Euler 公式近似为Fourier 级数:

2.2 弹体对高频射流的滤波特性

在脉冲直接力作用下，弹体呈现明显的低通滤波特性。以某弹体俯仰通道为例，飞行高度6 km，速度2Ma，R4喷口推力2 kN，滞后时间与斜边时间均为2 ms，理想脉冲信号占空比50%，则弹体对不同阶近似信号的响应过程如图2 ～3 所示。

图2 导弹对直接力信号的过载响应

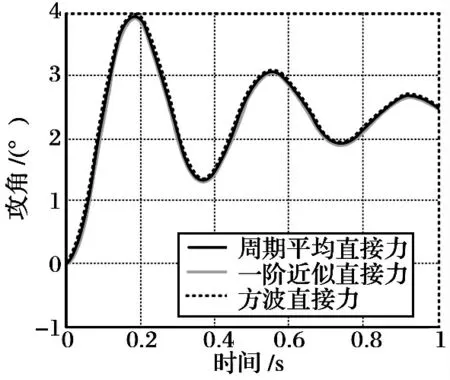
图3 导弹对直接力信号的攻角响应

可见，尽管采用不同近似项得到的等效推力幅值差异明显，但其对弹体的操纵响应却基本一致，这说明，对弹体这一低通环节而言，可以通过调节高频脉冲的占空比来实现不同的控制效果。当然，也正是由于弹体的这种低通滤波特性，才能把按脉冲调宽方式工作的控制系统看作是一个等效的比例式控制系统，即可以用等效的周期平均推力来代替离散脉冲推力，这样就能够运用传统的线性方法来分析弹体环节对指令的响应以及系统闭环的稳定性和制导误差等。

2.3 高频射流装置的连续性建模

为适用线性控制技术，需要对离散式高频射流装置连续性建模。直接力装置具有开关离散特性，根据前文结论，可将其等效为一阶连续环节:

式中:时间常数Tt包含滞后时间与斜边时间在内的所有延迟特性。

3 线性二次型协调控制器设计

LQR 问题按目标函数的形式不同可以分为三类:最优状态调节器问题、最优输出调节器问题、最优跟踪器问题。理论上可以证明:后两个最优问题均可以转化为状态调节器问题。

3.1 线性二次型最优控制技术

为使其标准化为易于LQR 方法处理的形式，同时考虑过载跟踪误差与舵机快速性限制，给定跟踪器问题的性能指标为

进一步剔除不可观状态量及其所在的状态方程，采用图4 所示的改进三回路控制结构，则对应的最优状态调节器问题性能指标可取为

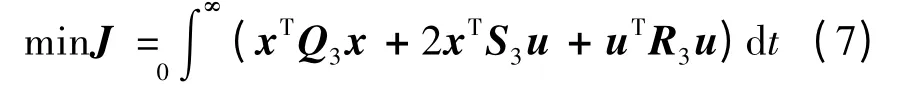
图4 所示最优跟踪器问题的输出反馈增益矩阵为

式中:Kopt3是对应于式(7)状态调节器问题的增益矩阵，可由扩展LQR 方法求得。

图4 改进的三回路控制结构

至此，由标准LQR 问题出发，经过一系列数学变换，便得到了扩展LQR 跟踪器问题的反馈增益矩阵。

3.2 控制量动态分配算法

为实现虚拟控制量到实际控制量的映射，不妨取虚拟控制量为v =［δMz］，实际控制量为u =［δzf］T，它们之间依然满足如下关系式:

式中:

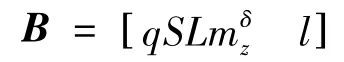
当考虑执行机构饱和约束时，问题可以描述为

该问题可采用求解线性不等式约束线性最小二乘问题的有效集算法来解决。

令δ = x－x(k)，bk= b－Ax(k)，可以把问题改写为寻优步骤如下:

步骤1:确定一个初始可行点x(1)及相应的有效集I，置k = 1;

步骤2:求优化问题的解δ(k);

步骤3:如果x(k)+δ(k)不可行，转到步骤6;

步骤4:置x(k +1)= x(k)+δ(k)，计算λk+1及λ(k+1)q;

步骤5:如果λ(k+1)q≥0，停止迭代;否则置Ik+1= {q}，并转步骤8;

步骤6:确定步长αk及指标p;

步骤7:置x(k +1)= x(k)+ αkδ(k);

步骤8:置k = k +1 后转步骤2。

4 仿真结果与分析

为验证带动态分配的控制效果，针对俯仰通道设计LQR 控制器，并采用有效集算法对虚拟控制量进行动态分配。同时，考虑气动舵偏角的位置约束为±30°，速率约束为±300(°)/s，角频率为120 rad/s，阻尼比为0.7。直接力装置的位置约束为±1，时间常数为0.02。则弹体对某弹道点的10g 与30g 过载指令跟踪及控制量分配情况，分别如图5 ～8 所示。

图5 小过载响应对比

图6 小过载控制量对比

由图5 ～6 可知，在响应小过载指令时，无论是否采用动态分配，控制量都能满足稳定跟踪要求。不同的是，考虑动态分配时，系统响应时间较快，超调量较小。然而，由图7 ～8 可知，在响应大过载指令时，考虑动态分配的控制系统能更好地跟踪过载指令，而未考虑动态分配的控制系统将开始发散，控制用量也趋于饱和。这说明，小过载指令对单一控制量需求较小，单纯气动舵或单纯直接力均能实现稳定跟踪。而大过载指令很容易使任一单一的控制量趋于饱和，必须采用动态分配协调两套操纵机构并行工作，从而实现全弹闭环系统品质最优。

图7 大过载响应对比

图8 大过载控制量对比

5 结 论

(1)姿控式直接力产生机动过载的机理与气动舵相同，都有赖于攻角的建立。故在大动压条件下，气动舵效率较高，直接力仅起到增效气动控制的作用。而在小动压条件下，直接力/气动力复合控制具有显著的快速性及稳定跟踪优势。

(2)线性二次型最优控制方法能够应对直接力/气动力复合控制导弹这类含有前馈项的非标准对象模型问题，所设计出的控制器能使导弹动态品质优良的同时兼顾跟踪误差及执行机构能耗等多项指标。

(3)加权矩阵对LQR 控制器品质影响明显，若选择不当，易遭遇执行机构饱和问题。而考虑动态分配的LQR 控制器能够有效缓 解加权矩阵选择时对人为经验的依赖，能够充分利用不同执行机构的动态特性差异，使之协调工作，从而实现控制分配的在线优化，保证整体控制效果良好。

参考文献:

［1］Roger R P. The Aerodynamics of Jet Thruster Control for Supersonic/Hypersonic Endo-Interceptors:Lessons Learned［C］∥The 37th Aerospace Sciences Meeting and Exhibit. Reno，1999.

［2］Kennedy K，Walker B，Mikkelsen C. Jet Interaction Effects on a Missile with Aero-Dynamic Control Surfaces［R］. AIAA 1999－0807，1999:1－3.

［3］Ridgely D B，Lee Yung，Fanciullo T. Dual Aero/Propulsive Missile Control-Optimal Control and Control Allocation［C］. AIAA Guidance，Navigation，and Control Conference and Exhibit，2006.

［4］Schroeder W K，Mansfield. Dual-Control Scheme for Improved Missile Maneuverability［P］. Patent Number:US RE37331，2001:1－5.

［5］Ridgely D B，Drake D，Triplett L，et al. Dynamic Control Allocation of a Missile with Tails and Reaction Jets［C］∥AIAA Guidance，Navigation，and Control Conference and Exhibit，Hilton Head，South Carolina，2007.

［6］钱杏芳，林瑞雄，赵亚男.导弹飞行力学［M］.北京:北京理工大学出版社，2000:175－233.