一种捷联惯性/GPS/陆基容错复合导航方案设计

王 勋，王新龙，车 欢

(1. 北京航空航天大学 宇航学院，北京 100191;2. 航天恒星科技有限公司，北京 100086)

0 引 言

捷联惯导具有自主性强、动态性高、隐蔽性好以及短时精度高等优点，但误差随时间积累［1－4］。而GPS 定位精度高、误差不随时间积累，且具有全球性、全天候的特点，但其动态性和抗干扰能力较差［5］。相比于GPS 系统，陆基导航系统在工作区内信号强度大且动态性要求低［6］，但定位精度相对较差，与GPS 系统有很强的互补性。因而，将SINS、GPS 和陆基导航系统进行优化组合配置，合理分配系统间的信息流程，对各子系统信息进行实时故障诊断与有效隔离，能够实现系统性能优势互补及保证冗余信息的有效利用。

基于此，本文设计一种SINS、GPS 以及陆基相结合的融合容错导航方案。采用具有两级结构的分散化联邦滤波方法，对信息分配系数进行自适应调节，以抑制环境和GPS、陆基导航子系统精度差异对滤波的动态扰动;采用双状态χ2检验法，利用两个状态递推器交替进行滤波校正与故障检测，在避免故障污染的同时，又可对故障子系统进行实时修复与隔离，从而构成了一种高精度的捷联惯性/GPS/陆基容错复合导航系统。

1 复合导航系统滤波模型

1.1 复合导航系统状态方程

1.1.1 捷联惯导系统误差模型

选择地理坐标系作为SINS 导航解算的基本坐标系，则SINS 系统误差模型如下所示:

式中:φn为失准角;δVn为速度误差;δλ 和δL 为经纬度误差;εb为陀螺仪漂移;εr为一阶马尔科夫过程;T 为相关时间;wr为白噪声;Δb为加速度计零偏;Re为地球半径。

将式(1)写成矩阵形式为

式中:

其中:FN为对应于SINS 的9个误差参数(3个姿态误差，3个速度误差，3个位置误差)的系统动态矩阵，为9 ×9 阶的方阵;FI阵的元素可参考文献［7］的附录。

1.1.2 GPS 导航系统误差模型

在GPS 定位测量误差源中，接收机钟差是造成GPS 定位的主要误差源，即使采用差分工作方式亦无法消除这一误差源［8］。在建立误差方程时，考虑到载体的高动态特性，加速度会造成钟频偏移。因而选取状态变量δt，δf，δfa分别为接收机钟偏、钟偏漂移和钟偏加速度漂移率，则可得GPS 误差方程为

结合捷联惯性导航系统的误差模型以及GPS导航系统的误差模型，可得SINS/GPS 子滤波器1的状态方程如下所示:

式中:

1.1.3 陆基导航系统误差模型

陆基导航系统中VOR(Very High Frequency Omnidirectional Radio Range)和 DME (Distance Measuring Equipment)的误差包含两个分量［9］:一个分量具有长的相关时间，其模型可建立为随机偏置;另一个分量具有短的相关时间，其模型可建立为白噪声。这些误差分量的均值事实上均为零。取bV，eV分别表示有长相关时间及短相关时间的VOR 误差分量，其数学模型可写为

取两个陆基地面站，并综合捷联惯性导航系统的误差模型以及陆基导航系统的误差模型，可得SINS/陆基子滤波器2 的状态方程如下所示:

式中:

1.2 复合导航系统量测方程

1.2.1 子滤波器1 量测方程

取SINS 与GPS 输出的速度和位置之差作为量测，定义位置量测方程为

定义速度测量方程为

式中:

联立位置和速度量测方程，得到子滤波器1 的量测方程为

1.2.2 子滤波器2 量测方程

取两个陆基地面站，设矢量R1，R2，R12分别用东向、北向及天向表示(x1，y1，h1)，(x2，y2，h2)，(x12，y12，h12)，其中取V1和D1，V2和D2分别表示从地面站1 和地面站2 得到的测量值。由此可得

将上式在标称飞行轨迹附近展开成泰勒级数，并取一阶项，可得如下量测方程:

式中:

点 评：小作者以一双自由的的眼睛上天、入地、下海、遨游太空，展现了他渴求知识、探寻未知，肩负家国，心怀世界的胸襟，是一篇难得的想象诗。

2 复合导航系统的容错性滤波方案设计

单状态χ2检验法是复合导航系统故障检测常用的方法［10］，但直接将其应用于复合导航系统的故障检测会存在以下问题［11］:由于在状态递推器中没有量测更新，模型误差、系统噪声与滤波初值误差会导致状态递推值偏离真实值，使状态检测函数不能实时跟踪故障变化，其直接结果是降低了检测灵敏性，而周期性地用滤波结果来重置状态递推器又会使其受到故障污染。双状态χ2检验法是在单状态χ2检验法的基础上发展起来的一种新的故障检验方法［12］，它是利用两个状态递推器，交替地用子滤波器信息重置和故障检测。并采用对状态元素进行单独检测的方法，以获得故障对某一状态的影响程度大小。

2.1 双状态χ2 检验法

式中:β(k)服从高斯分布，且均值为零，设其方差为B(k)。

当子系统发生故障时，通过检验β(k)均值即可确定系统是否发生了故障。对β(k)作如下的二元假设:

H0:系统无故障

H1:系统有故障

根据β(k)及其方差B(k)，构建故障检测函数:

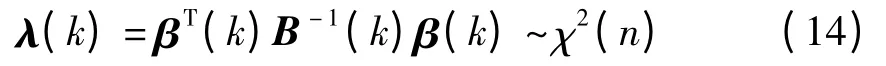
式中:B(k)表达式为

为了获取故障对某一状态的影响程度，考虑对β(k)中的元素进行单独检测，则对于β(k)中第i个元素，有

式中:Bi，i(k)为方差矩阵B(k)中对角线上的元素。

若定义变量ζβi如下:

则可采用如下判定准则进行故障检测:

式中:εβi为检测门限，由预先给定的误警率依据奈曼－皮尔逊准则得到。

采用上述判定准则，即可对不同状态进行检测，受故障污染最严重的状态将首先被检测出来。图1 为基于双状态χ2检验法的故障检测实现结构框图。

图1 基于双状态χ2 检验法的故障检测原理

图1 中，子滤波器和双状态递推器同步执行，子滤波器由传感器量测数据驱动，输出包含有量测更新的状态估计及其方差Pz(k)。设在ti(i=1，2，…，n)时刻，利用状态估计)对任一个状态器进行重新赋值，其他时刻ti≤k ＜ti+1(i =1，2，…，n)工作于故障检测状态。当k=t2i－1(i=1，2，…，n)时，开关K1处于1 处，重置状态递推器I;当t2i－1≤k ＜t2i时，开关K2处于2 处，此时状态递推器Ⅱ进行故障检验。当k =t2i(i =1，2，…，n)时，开关K1处于2 处，重置状态递推器Ⅱ。当t2i≤k ＜t2i－1时，开关K2处于1 处，此时状态递推器I 处于故障检验状态。故障检验采用状态χ2检验法，通过给定的误警率得到检测门限，以获取系统故障状况。

2.2 故障隔离策略

系统检测出故障状态后，就需要及时隔离故障子系统，采取如下故障隔离准则:

(1)若子系统SINS/陆基或SINS/GPS 其中一个发生故障，认为局部估计或失效，则不将其输入主滤波器。此时，系统误差状态的整体估计为

(2)若两个子系统同时发生故障，主滤波器将直接输出惯导系统的状态:

根据上述故障隔离策略，只利用未失效的量测驱动子滤波器进行状态估计，同时对失效的子系统进行故障修复。当失效的子系统重构完毕，则相应子滤波器又可提供正确的局部状态估计值，将其输入主滤波器，使该组合导航系统重新为系统提供连续、精确的导航信息。

2.3 基于双状态χ2 检验法的容错融合方案

采用两级数据融合形式的联邦滤波器，先分散处理，再全局融合，它具有设计灵活、计算量小、容错性能好等优点［13］，是提高复合导航系统的精度和可靠性的行之有效的融合方法。所设计的捷联惯性/GPS/陆基容错导航系统的信息融合流程框图如图2 所示。

图2 捷联惯性/GPS/陆基容错导航系统信息流程框图

图2 中，两个子系统SINS/GPS、SINS/陆基经过两个子滤波器后，送入相应的故障检测单元，利用双状态χ2检验法检测故障状态，并判别子滤波器输出是否可用，仅将可用的估计值送入主滤波器，以给出可靠的全局最优误差状态估计值同时，将全局最优估计及其相应的协方差β－1iPg反馈到子滤波器，以重置子滤波器的估值。

由于各子滤波器之间彼此相关，需要采用信息分配原理实现联邦滤波解算。而对于动态较高的载体，动态模型误差偏差较大，同时GPS、陆基系统的定位精度差异，环境因素引发的各种输出误差或异常，均可能使滤波系统产生扰动。考虑到滤波误差协方差阵P 能够反映导航传感器精度差异与环境干扰的综合性能。因而，联邦滤波信息分配系数如下形式:

式中:tr(Pi)为矩阵Pi的迹;其值越小，则第i个子滤波器的估计精度越高，对全局估计的利用权重就越大。

需要指出的是，主滤波器根据环境扰动与实际传感器精度动态调整信息分配系数βi，控制GPS和陆基导航子系统的信息融合等级，并将主滤波信息反馈到子滤波器进行校正，这实际上间接地利用高精度GPS 信息来提高陆基定位精度，从而提高整体估计精度。

3 仿真验证

3.1 仿真条件设定

仿真时间为600 s，SINS 解算周期为0.01 s，子滤波器和主滤波器滤波周期均为1.0 s。仿真中，设置两种类型的故障:硬故障(突变故障)和软故障(缓变故障)，具体如表l 所示。

表1 故障检测方案的故障设置

仿真条件分别设定无故障、硬故障(突变)和软故障(缓变)三种不同情况，其中，无故障设定SINS、陆基以及GPS 均正常工作;硬故障设定GPS和陆基分别在100 ～150 s 和350 ～450 s 时间段，突变大小分别为0.08'和0.10';软故障设定GPS和陆基分别在200 ～250 s 和500 ～550 s 时间段，GPS 在三个方向上的位置误差每秒均增大0.001'，陆基在三个方向上的位置误差每秒均增大0.001 5'，缓慢变化后均即时恢复正常状态。

3.2 仿真结果及分析

3.2.1 故障检测性能仿真与验证

针对无故障、硬故障(突变)和软故障(缓变)三种不同仿真条件，采用双状态χ2检验法对三种不同形式的工作状态进行检测。

(1)无故障情况

图3 ～4 为陆基和GPS 子系统的故障检测函数计算值与告警输出曲线，根据给定的误警率0.1%设置检测门限为10.83，发生故障时即检测函数值高于检测门限则告警输出为“50”，否则输出为“0”。可以看出，无故障时两个子系统均正常工作，告警输出始终为“0”，没有误警发生。

图3 陆基子系统故障检测与告警输出

图4 GPS 子系统故障检测与告警输出

(2)硬故障(突变)情况

图5 ～6 为设置硬故障时，陆基和GPS 子系统输出的位置误差曲线。

图5 陆基子系统输出的位置误差曲线

图6 GPS 子系统输出的位置误差曲线

图7 ～8 为设置某时段突变故障条件下，陆基和GPS 子系统的故障检测函数计算值与告警输出曲线。其中，陆基和GPS 子系统故障检测单元分别在351.3 s 和100.3 s 时刻出现告警，判定系统开始发生故障，告警结束时刻分别为401. 8 s 和154.2 s，系统恢复正常。可见，两个子系统的告警开始与结束时刻均有一定的延迟，这与检测周期及每个故障检测周期内故障判定次数的选取有关，判定次数越大，检测灵敏度越高但计算量也随之增大。

图7 陆基子系统故障检测与告警输出

图8 GPS 子系统故障检测与告警输出

(3)软故障(缓变)情况

图9 ～10 为设置软故障时，陆基和GPS 子系统输出的位置误差曲线。

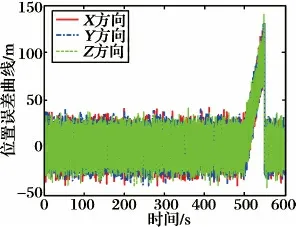
图9 陆基子系统输出的位置误差曲线

图10 GPS 子系统输出的位置误差曲线

图11 ～12 为设置某时段软故障条件下，陆基和GPS 子系统的故障检测函数计算值与告警输出曲线。从图中可以看出，故障检测单元检测出的故障时刻为506.8 s 和205.2 s，实际故障的发生时间是500 s 和200 s，检测出故障的时间分别比实际故障时间延迟6.8 s 和5.2 s，这是由于缓变故障开始的一段时间内，故障很小，检测函数值也很小，而随着故障增大，检测函数值逐渐增大，当超过检测门限时，故障出现告警。需要指出的是，缓变故障在被检测出之前，其对导航精度的影响较小。

图11 陆基子系统故障检测与告警输出

图12 GPS 子系统故障检测与告警输出

从对上述三种故障情况的检测结果可以看出，故障检验单元能够有效判别故障与否，并可以检验出突变故障和缓变故障，且具有较高的检测灵敏度。

3.2.2 故障隔离性能仿真与验证

利用600 s 仿真数据进行仿真，两个状态递推器交替检测时间间隔为2.0 s。为了验证算法对任一子系统发生故障后进行隔离与修复的有效性，使用表1 的故障设置条件，故障隔离后的滤波结果如图13 ～14 所示。

图13 故障隔离后滤波位置误差

图14 故障隔离后滤波速度误差

从图13 ～14 可以看出，故障隔离后的位置误差限制在5 m 以内，速度误差在0.2 m/s 以内，故障隔离后的滤波精度较高。这是由于故障检测单元在检测出子系统发生故障后，快速隔离故障子系统，使其子系统输出值不进入主滤波器。此外，由于主滤波器不断地对两子滤波器进行重置，利用各子系统的误差协方差阵，对信息分配系数进行自适应调节，有效抑制了环境干扰和GPS、陆基子系统精度差异对滤波的扰动，从而使精度相对较低的陆基系统子滤波器能够不断地得到主滤波器的滤波反馈信息来提高精度，充分保证了主滤波器输出的准确性和实时性。

4 结 论

设计了一种基于双状态χ2检验法的捷联惯性/GPS/陆基容错复合导航方案，利用导航子系统误差协方差阵对信息分配系数进行动态调节，能够适应环境与传感器精度的实际变化;设计的基于双状态χ2检验法的故障诊断方案和容错策略，能够有效诊断并隔离GPS 和陆基导航子系统的突变、缓变故障，具有较高的工程应用价值。

［1］于洁，王新龙. SINS/GPS 紧密组合导航系统仿真研究［J］.航空兵器，2008(6):8－13.

［2］李佩娟，徐晓苏，王立辉，等. 水下无源组合导航系统智能容错方法设计［J］. 中国惯性技术学报，2013(2).

［3］王龙，张拥军，张文山，等. 地面系下的GPS/SINS 组合导航算法设计［J］. 航空兵器，2010(3):15－17.

［4］李鹏，赵兴锋，郑志强. SINS/TACAN/ADS/OES 机载组合导航设计与仿真［J］. 航空兵器，2008 (5):21－24.

［5］任建辉，苏祥荣，王文辉，等. 容错捷联惯性/星光/卫星组合导航技术研究［J］. 战术导弹控制技术，2010，27(2):1－5.

［6］方凌. 民航陆基近距无线电建模与机载综合导航可靠融合技术［D］. 南京:南京航空航天大学，2012.

［7］董绪荣. GPS/INS 组合导航定位及其应用［M］. 长沙:国防科技大学出版社，1998.

［8］申功勋，孙建峰. 信息融合理论在惯性/天文/GPS 组合导航系统中的应用［M］. 北京:国防工业出版社，1998.

［9］李正强，王宏力，杨益强，等. 信息融合技术在组合导航系统中的应用［J］. 飞行力学，2006，24(1):89－92.

［10］Brumback B，Srinath M D. A Fault－Tolerant Multisensor Navigation System Design［J］. IEEE Transactions on，Aerospace ＆ Electronic Systems 1987，23(6):738－756.

［11］Da Ren，Lin Chingfang. Failure Detection and Isolation Structure for Global Positioning System Autonomous Integrity Monitoring［J］. Journal of Guidance Control and Dynamics，2012，18(2):291－297.

［12］Da Ren. Failure Detection of Dynamical Systems with the State Chi-square Test［J］. Journal of Guidance Control and Dynamics，1994，17(2):271－277.

［13］贺元军，董鹏. 多模复合制导中多传感器分布式融合技术研究［J］. 航空兵器，2010(3):9－14.