基于改进引力搜索算法的稀布同心圆环阵优化

袁建涛，杨 晖，梁 静，张闻涛，稂华清，2

(1.中国空空导弹研究院，河南 洛阳471009;2.航空制导武器航空科技重点实验室，河南 洛阳471009)

0 引 言

圆口径天线阵能在上半空间范围形成任意方向的波束，同时圆结构口面的对称性使波束形状和天线增益基本保持不变。这些优点使圆面阵在雷达、声呐、卫星通信等领域得到日益广泛的应用。但由于均匀圆面阵方向图具有较高的旁瓣电平，使其在应用中受到限制。降低旁瓣电平的方法有多种，包括激励幅值优化、相位优化及阵元位置优化等。具有最小阵元间隔约束的同心圆环阵可以采用稀疏和稀布两种优化方案在减少一定数量单元数的同时来降低旁瓣电平，但稀布优化比稀疏优化有着更大的优化自由度，可以得到更低的旁瓣电平，且国内外鲜有研究。

稀布天线阵列优化设计是一个复杂的非线性优化过程，随机性和鲁棒性强，在对搜索空间没有特殊要求的智能算法稀布阵或稀疏阵综合中得到广泛的应用，并取得了良好的结果。引力搜索算法(Gravitational Search Algorithm，GSA)［1－5］是近几年提出的一种新的智能优化算法，它基于牛顿万有引力定律，依靠群体中粒子间的相互作用力产生群体智能，进而指导种群的优化搜索方向，现已成功应用于数字滤波器的设计、天线阵列综合、无人机航迹规划等。文献［6］通过算法性能对比，证明GSA 与遗传算法(Genetic Algorithm，GA)［7］和粒子群算法(Particle Swarm Optimization，PSO)［8］相比收敛性能更优，但同样存在早熟收敛问题。

为了解决标准引力搜索算法早熟收敛问题，提出一种改进的GSA(IGSA)，用于具有阵元间隔约束的同心圆环阵阵元数目和阵元分布联合优化。通过对粒子惯性质量进行基于适应度值的线性加权，强化优性能粒子，弱化劣性能粒子，加快算法的收敛速度;引入遗传算法的变异算子，通过大概率的基因变异，改善GSA 的种群多样性及局部搜索能力，解决算法早熟收敛问题。仿真结果证明，IGSA 收敛性能优于标准GSA。

1 引力搜索算法

自然界中，万有引力无处不在且不可躲避，粒子会在万有引力作用下相互吸引，如图1 所示。

图1 万有引力作用

和粒子群算法一样，引力搜索算法首先对粒子的位置和速度进行初始化。设种群中有N个粒子，搜索空间为D 维，则第i个粒子定义为

式中:Maj(t)和Mpi(t)分别为粒子j 和粒子i 的惯性质量;ε 为一个很小的常数;Rij(t)为第i 和第j个粒子之间的欧氏距离;G(t)为t 时刻的引力常数。Rij(t)和G(t)的表达式分别为

式中:G0为引力常数的初始值;α 为衰减速率;T为最大迭代次数;本文G0取10，α 取5。

式中:randj为［0，1］之间的随机数;Mi(t)为第i个粒子的惯性质量。

粒子的速度和位置在迭代过程中的更新为

在GSA 中，粒子的惯性质量与适应度值的大小有关，惯性质量的更新如下:

式中:fiti(t)为t 时刻第i个粒子的适应度值。对于求适应度最小值，worst(t)和best(t)定义为

2 改进后的引力搜索算法

在GSA 中，粒子的惯性质量正相关于其适应度值。惯性质量线性加权是指在每次迭代过程中，根据计算得到的适应度值，对每个粒子的惯性质量Mi(t)乘以相应的比例因子，使惯性质量大的粒子惯性质量更大，惯性质量小的粒子惯性质量更小，以加快算法收敛速度。该比例因子β 定义为

式中:M'i(t)为更新质量;wmax为最大权值，取值0.7;wmin为最小权值，取0.1;avg(t)为第t 代的平均适应度值。

为保持种群多样性，引入遗传算法变异算子，采用自适应变异概率，定义为

式中:pmmax和pmmin分别为最大和最小变异概率，取pmmax= 0.2，pmmin= 0.1［9］。

假设阵元i 对应的随机数pi产生变异，则变异后的随机数为

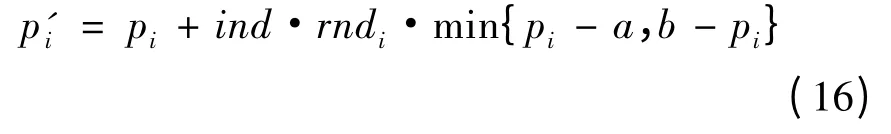
式中:p'i和pi均为实数;ind 为系数，文中取值0.3;rndi∈［－1，1］;a 和b 分别为规定的随机数的下限和上限。

3 算法步骤

改进引力搜索算法的具体执行步骤如下:

(1)粒子位置和速度的初始化;

(2)计算粒子适应值，并保留最佳个体;

(3)更新引力系数G(t)、最优适应度值best(t)、平均适应度值avg(t)、最坏适应度值worst(t)及各个粒子的惯性质量Mi(t);

(4)由式(2)计算粒子各方向所受作用力;

(5)由式(5)～(6)更新粒子加速度和速度;

(6)根据式(7)更新粒子的位置;

(7)计算各个粒子的自适应变异概率，进行变异操作;

(8)当满足最大迭代次数或精度要求退出循环，否则返回步骤(2)进行循环迭代;

(9)结束循环，输出结果。

4 稀布同心圆环阵的多约束模型

多个阵元沿圆环排列构成圆环阵列，当多个同心圆环阵列的阵元在各圆环上满足最小阵元间隔约束并随机分布时，便构成了稀布同心圆环阵列，阵列模型如图2 所示。

图2 稀布同心圆环阵

图中，极坐标(ρn，φn)表示第n个阵元的位置，其激励为Inexp(jξn)。设所有阵元为全向辐射单元，则天线阵列的辐射方向图表达式为

式中:λ 为工作波长;θ 和φ 分别为俯仰角和方位角，0 ≤θ ≤π/2，0 ≤φ ≤2π。

设同心圆环阵的圆环个数为M，圆环半径为ρ0，ρ1，…，ρM，通过优化各个圆环上阵元的数目和位置，以获得峰值旁瓣电平最低的稀布同心圆环阵。该最优化问题的数学模型为

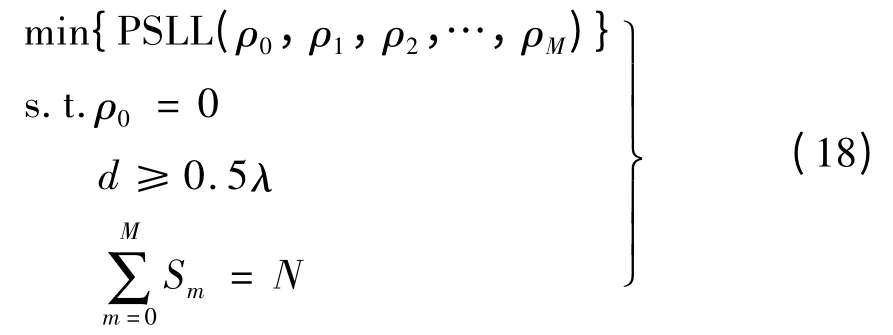
式中:PSLL(ρ0，ρ1，ρ2，…，ρM)=max{| F(θ，φ)/FFmax|}，F(θ，φ)中的θ 和φ 在旁瓣区域内取值，FFmax为主瓣最大值;d 为相邻阵元的弧向间距;Sm为第m个圆环上的总阵元数。

5 同心圆环阵与直线阵之间的相互转换

由M个圆环组成的同心圆环阵从与x 正半轴相交处断开逆时针方向展开并按序号组成一条直线段，该线段长度为

设同心圆环阵稀布率为f，稀布后阵元个数为N，最小阵元间距dc= 0.5λ。为了满足同一圆环起始阵元和末尾阵元间隔约束，每个圆环的最后dc内不能放置阵元，则虚拟直线阵列的有效长度为

按照文献［10］固定起始阵元和末尾阵元进行种群初始化，此时，将线阵上阵元位置映射到同心圆环阵列上的位置分布。当确定第m个圆环上首个阵元在直线阵列上的位置时，其后面2πρm－dc范围内的阵元在同一圆环上，均满足最小间隔约束。设第m－1个圆环首个阵元在直线阵列上的位置为xp，第m个圆环首个阵元在直线阵列上的位置为xn，阵元在直线阵列上的位置为x，当其满足

其对应的圆环半径ρ = ρm，位置角度φ 为

根据式(21)～(22)，直线阵列上位置x 对应同心圆环阵列极坐标(ρ，φ)，根据式(18)计算粒子适应度值。

6 综合结果

设有一均匀同心9 圆环阵列天线，圆心处放置天线单元，阵元总数为279，其阵面分布如图3 所示。阵元均为理想的全向单元，阵元激励为1，相邻圆环径向间距为Δr = λ/2，阵元间距d ≅λ/2，则第m个圆环上的阵元数为

式中:floor 表示向下取整，其PSLL 为－17.40 dB 。

图3 均匀分布的同心9 圆环阵

取稀布率为66%，则阵元数目为185，阵元间距d ≥λ/2，相邻圆环径向间距Δr = λ/2 的约束条件下分别运用GSA 和IGSA 对阵列进行5 次稀布优化，使其PSLL 最低。GSA 和IGSA 基本参数设置为:种群数200，最大迭代次数200。阵列优化结果如图4 ～6 和表1 所示，算法最优收敛曲线如图7所示，收敛性能对比如表2 所示。

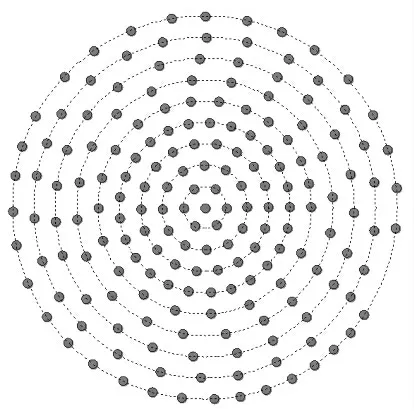
图4 IGSA 优化得到的稀布同心9 圆环阵

图5 优化后的同心圆环阵方向图

图6 两个主截面方向图

图7 GSA 和IGSA 的最优收敛曲线

表1 同心9 圆环阵列的稀布优化结果

表2 GSA 和IGSA 分别优化5 次的收敛性能对比

表1 中，IGSA 的最优PSLL 为－25.10 dB，比均匀同心9 圆环阵的PSLL 降低了7.70 dB;比文献［11］中运用经典遗传算法得到的最优稀疏同心9 圆环阵列的PSLL 值－22.44 dB 降低2.66 dB;比文献［12］中运用修正遗传算法得到的最优稀布同心9 圆环阵的PSLL 值－23.74 dB 降低1.36 dB;比标准GSA 得到的最优稀布同心9 圆环阵的PSLL值－23.85 dB 降低1.25 dB。

通过改进前后引力搜索算法收敛曲线的对比可知，IGSA 的收敛性能和速度均优于GSA，从而证明了改进策略的有效性。文中提出的IGSA 在提高算法收敛速度的同时，改善了最优解的质量，解决了GSA 易早熟收敛的问题。

7 结 论

对GSA 进行改进，通过引入惯性质量加权因子，加快了算法的收敛速度，又引入遗传算法的变异算子，提高了引力搜索算法的局部搜索能力并改善了种群多样性，解决了引力搜索算法易早熟收敛的问题。最后将改进的GSA 成功应用于同心圆环阵稀布优化，并得到良好的旁瓣性能。该算法对搜索空间没有特殊要求，可以满足各种应用要求。

［1］Sarafrazi S，Nezamabadi-Pour H，Saryazdi S. Disruption:a New Operator in Gravitational Search Algorithm［J］.Scientia Iranica，2011，18(3):539－548.

［2］Rashedi E，Nezamabadi-Pour H，Saryazdi S. GSA:A Gravitational Search Algorithm［J］. Information sciences，2009，179(13):2232－2248.

［3］李沛，段海滨. 基于改进万有引力搜索算法的无人机航路规划［J］. 中国科学:技术科学，2012，42(10):1130－1136.

［4］徐遥，王士同. 引力搜索算法的改进［J］. 计算机工程与应用，2011，47(35):188－192.

［5］李春龙，戴娟，潘丰. 引力搜索算法中粒子记忆性改进的研究［J］. 计算机应用，2012，32(10):2732－2735.

［6］Li Chaoshun，Zhou Jianzhong. Parameters Identification of Hydraulic Turbine Governing System Using Improved Gravitational Search Algorithm［J］. Energy Conversion and Management，2011，52(1):374－381.

［7］Haupt R L. Thinned Arrays Using Genetic Algorithms［J］. IEEE Transactions on Antennas and Propagation，1994，42(7):993－999.

［8］Robinson J，Rahmat-Samii Y. Particle Swarm Optimization in Electromagnetics［J］. IEEE Transactions on Antennas and Propagation，2004，52(2):397－407.

［9］韩万林，张幼蒂. 遗传算法的改进［J］.中国矿业大学学报，2000，29(1):102－105.

［10］陈客松，韩春林，何子述. 一种有阵元间距约束的稀布阵天线综合方法［J］. 电波科学学报，2007，22(1):27－32.

［11］Haupt R L. Optimized Element Spacing for Low Sidelobe Concentric Ring Arrays［J］. IEEE Transactions on Antennas and Propagation，2008，1(56):266－268.

［12］于波，陈客松，朱盼，等. 稀布圆阵的降维优化方法［J］. 电子与信息学报，2014，36(2):476－481.