基于改进RBF-NN优化模糊PID控制器的设计方法
王嘉轶,闻 新
(南京航空航天大学 航天学院,南京 210016)
0 引 言
雷达伺服系统通过雷达天线进行实时跟踪,是雷达系统的一个重要组成部分,伺服系统的好坏直接影响到雷达系统的测量精确程度[1]。传统的雷达伺服系统一般采用PID 控制,主要通过调节P(比例)、I(积分)、D(微分)三个参数对控制对象进行控制,表现为对控制偏差的影响以及对控制误差、误差变化和误差累积的计算和调节[2]。常规的PID 控制器因其结构简单、易实现的特点在控制领域被广泛使用。但是,当面对非线性问题以及复杂战场环境并且有干扰因素影响时,常规的PID 控制器需要人工实时调节P,I,D 的参数值,才能够满足系统的需求,这是不现实的。所以,研究如何优化PID 控制器成为关注的重点。
为了提高PID 控制器系统的能力,提出基于遗传算法改进的径向基函数神经网络的模糊PID控制器。该PID 控制器系统融合了神经网络自学习、自组织、自适应的能力,遗传算法的优胜劣汰原则以及模糊控制推理能力强的特点,更适合于解决非线性复杂系统的问题[3-7]。文中对径向基函数神经网络、遗传算法以及T-S 模糊控制进行详细的分析和计算,并通过MATLAB 仿真应用验证了所提方法的正确性和有效性。
1 径向基函数神经网络控制器设计
径向基函数神经网络(RBF 神经网络)是由Moody 和Darken 在20 世纪80年代末提出的一种单隐层的三层前馈神经网络[8],一般包含输入层、隐含层和输出层,如图1 所示。

图1 RBF 神经网络结构图
在RBF 神经网络结构中,输入层由信号源节点构成,是用来接收输入信号的,网络的输入向量为X=[x1,x2,x3,…,xn]T,并且RBF 神经网络对输入样本没有特定要求。隐含层作为RBF 神经网络中最重要的部分,其神经元采用的是径向基函数H=[h1,h2,…,hj,…,hm]T,其中将径向基函数取为高斯函数,即

式中:Cj为第j个节点的中心矢量,Cj=[Cj1,Cj2,…,Cji,…,Cjn]T,i =1,2,…,n;bj为节点j 的宽度参数;m 为隐含层节点数[9]。隐含层到输出层使用的是线性函数,输出层只实现对隐含层节点非线性输出的线性组合。此外,RBF 神经网络具有在线学习和快速收敛的特性。因此,可以用RBF 神经网络来实现对PID 控制器的参数整定并以此来控制系统的误差。
基于RBF 神经网络的自适应PID 控制器的改进算法如下[10-11]:

式中:wj为隐含层节点hj至输出层节点的连接权值;μ 为学习速率;u(k)为控制输入值。PID 的参数Kd,Kp,Ki是通过RBF 神经网络在线算法的自适应整定来控制e(k)的。MATLAB 提供了两个命令newrb 和newrbe 来设计RBF 神经网络,newrb 通过逐渐增加径向基神经元的个数进行长期训练来控制误差的标准;newrbe 通过构建网络来快速控制误差。在RBF 神经网络的学习算法中,先根据输入样本来确定隐含层各节点的中心向量Cj和宽度参数bj,再求出连接权值wj[12]。
2 基于遗传算法的PID 参数整定
遗传算法是基于自然界“适者生存”机制并通过信息交换来获得最优解的估计方案,是解决优化问题的一种高效方法。特别是对于一些非线性模块的函数优化问题,它可以快速方便地达到最佳的函数优化结果。与模拟退火算法等其他优化算法相比,它表现出更好的全局搜索能力,收敛速度快,并且不会陷入局部最优解的问题当中。该算法主要是由染色体编码方法、适应度评价、遗传算子以及基本遗传算法的运行参数构成的。
2.1 遗传算子
在生成初始种群后,遗传算法通过使用复制、交叉和变异算子来产生后代,取代一部分老一代种群,形成优于老一代的新种群。随着群体的不断优化,遗传算法寻找最佳的个体来逐渐接近最优解,最终达到求解最优解问题的目的。遗传算子的设计十分关键,因为这些都是模拟自然界物种的繁衍、杂交以及突变过程,使适应度高的个体被保留下来,组成新的群体,新的群体继承并优于上一代,是非常重要的过程[13]。
2.1.1 复制
在复制过程中,群体中个体的选择是取决于他们的适应度值。适应度越高的个体将有越多的机会繁殖后代,也就是说在下一代中得到更多的生存机会。主要的选择方法有排序选择法、适应值比例选择法和联赛选择法等。本文采用的是联赛选择法,基本思想是从现有群体中通过随机的方式选择一定数量的个体,将其中适应度最大的个体保留下来[14]。通过反复执行这个过程,直到下一代的个体数量能够填满交配池。
2.1.2 交叉
复制操作只是从上一代种群中选择适应度高的个体保留下来,但不能创造出新的染色体个体,而交叉操作可以实现这一过程。遗传算法全局搜索性能主要由交叉算子来决定。交叉算子是指由适应能力强的父辈染色体作为双亲进行繁殖以得到更优秀的下一代。交叉概率范围一般取0.6 ~1。如果父辈染色体位置相互靠近,那么新生成的染色体位置也会更加靠近父辈染色体。因此,搜索将变得更加具有随机性。
2.1.3 变异
变异算子在交叉运算结束后进行,在变异的过程中,新的染色体加入到了种群中。变异是使染色体信息随机发生微小变化的过程,这种过程不是在所有染色体中都会发生的。变异主要是为了改善遗传算子的局部搜索能力,同时也加强群体的多样性。文中采用的主要是均匀变异算子。
2.2 通过遗传算法改进RBF 神经网络
RBF 神经网络是一种性能优良的前馈型神经网络,具有任意精度逼近任意非线性函数的能力,且拓扑结构紧凑、收敛速度快。但由于系统结构复杂性和数据量的增大,RBF 神经网络也不能完全避免陷入局部极小值的问题。特别是隐含层节点中心值和宽度的选取对RBF 神经网络的函数逼近能力具有重要影响[15]。本文利用遗传算法的全局搜索能力对RBF 神经网络中隐含层的中心值和宽度进行优化处理,以保证能够找到权值的最优解。
在RBF 神经网络结构固定的前提下,用遗传算法替代RBF 网络学习算法,从而进行网络权系的训练,优化其权系值。基于遗传算法的RBF 神经网络结构优化步骤如下:
(1)设定网络的种群规模为N,随机产生初始种群并用二进制编码方式对RBF 神经网络中的权值进行编码;
(2)设置GA 参数及自适应调整算法;
(3)译码种群中的每一个个体位串,求得N组网络权系值,得到有相同结构的N个网络;
(4)由输入样本集经前向传播算法,求得N组网络权系值对应的N个网络输出;
(5)设定网络的目标函数,将其转换成适应度值,对N个网络进行评价;
(6)依据适应度值在GA 空间进行复制操作;
(7)依据选定的交叉、变异及有关算法、参数,进行相应的操作,得到新一代种群;
(8)返回步骤(3),直到满足性能要求,得到一组优化的权系值。
2.3 通过遗传算法对PID 进行参数整定
PID 控制器最优参数是通过基于遗传算法优化的RBF 神经网络的整定而获得的。此过程主要包括变量符号的选择和适应度函数的调整。
2.3.1 变量表示
PID 控制器参数整定问题的元素包括比例增益Kp、积分增益Ki和微分增益Kd。这种先将整定变量直接表示的方法大大降低了计算机对种群数量的存储空间。所以,参数值是通过基于遗传算法改进的RBF 神经网络程序来对PID 控制器进行最优整定而获得的。
2.3.2 适应度函数
上述参数表示方法是非负适应度函数最大化的评估结果,而适应度函数值与目标函数值是线性相关的。所以,参数设置的评估可以将目标函数F(Kp,Kd,Ki)作为标准,而适应度函数则由目标函数的相关标准确立。因此,可以将性能标准的极小值问题转化为适应度函数的极大值问题来求解:

式中:k 是常数;ITEA 是时间乘以误差绝对值的积分,即

式(5)的作用是为了增大1/F 的值,使染色体的适应度值可以在一个相对更大的范围内进行。
RBF 神经网络整定的PID 控制器以误差和误差变化率为输入,经过遗传算法优化处理后,得到输出为ΔKp,ΔKd,ΔKi的参数值。为了尽量降低误差,一般会选择适应度较高的种群进行复制、交叉和变异操作。通过遗传算法对隐含层节点中心值、隐含层节点宽度和输出线性权值的优化,保证RBF 神经网络能找到全局最优解。
3 T-S 模糊控制
T-S 模糊控制由日本学者Takagi 和Sugeno 共同提出,其模糊规则为

式中:A 和B 是前件中的模糊集合;x 和y 是输入变量;f(x,y)是后件的精确函数;每个变量的模糊集合是由其对应的隶属函数来表示的。与mamdani 模糊系统模型相比,T-S 模糊控制输出的量非模糊量,而是精确的常量或者线性函数[16]。T-S 模糊系统的核心就是由一组这样的规则而形成的。在精确的输入信号条件下,模糊系统定义好模糊规则,然后计算出两个步骤下的有效输出:首先,求得每个规则下隶属度函数输入ωi的最小值;然后,通过式(7)根据每个规则输出的加权平均来计算出整体输出值:

本文中各种操作条件下的PID 控制器参数都是由S-T 模糊系统来确定的。
4 PID 控制器的设计方法
PID 参数的实时优化通过T-S 模糊控制器完成。其中:误差e 和误差变化率ec 是输入参数;ΔKp,ΔKd,ΔKi为输出值。误差e 和误差变化率ec论域上定义七个模糊子集,分别是{负大(NB),负中(NM),负小(NS),零(ZO),正小(PS),正中(PM),正大(PB)},其隶属度函数选为全交叠的正态型。通过遗传算法改进的RBF 神经网络可以对PID 的输入输出参数进行优化处理,每次优化过程中输入值e 和ec 组合下对应的最优控制参数可作为模糊PID 控制器的控制规则参与PID 控制器最后的参数整定过程。基于e 与ec 的每种组合形式,由遗传算法改进的RBF 神经网络给出了对应的ΔKp,ΔKd,ΔKi最优数值。对于某一雷达伺服系统,根据系统内部机构和变化,可将其等效为以下传递函数:

5 仿真结果
对于模糊逻辑工具箱(FIS)编辑器,将模糊控制的输入定义为误差e 和误差变化率ec,输出经处理后得到PID 的优化参数Kd,Kp,Ki。根据实际情况,规定误差e 的范围是-6 <e <6,ec 的范围是-3 <ec <3,而ΔKd,ΔKp,ΔKi的输出取决于e 和ec 的变化。将误差e 和误差变化率ec 的论域定义为{NB,NM,NS,ZO,PS,PM,PB},其隶属度函数如图2 ~3 所示。

图2 e 的隶属度函数图
经过基于遗传算法的RBF 神经网络操作后,误差e 和误差变化率ec 与对应关系下的ΔKp,ΔKi,ΔKd的值也确定下来,并可将其作为模糊控制器的模糊规则来处理,如表1 ~3 所示。

图3 ec 的隶属度函数图

表1 e 和ec 对应关系下的ΔKp

表2 e 和ec 对应关系下的ΔKi

表3 e 和ec 对应关系下的ΔKd
将模糊控制器输入输出的对应参数值都输入到模糊逻辑编辑器中,得出相应Kp,Kd,Ki输出特性曲面图以及模糊规则观察器,如图4 ~6 所示。
利用simulink 程序对雷达伺服系统的PID 控制模型进行搭建与仿真,为便于比较,将传统PID控制器与本文设计的模糊PID 控制器放在同一程序中进行设计,仿真效果图如图7 所示。

图4 Kp 的输出特性曲面

图5 Ki 的输出特性曲面

图6 Kd 的输出特性曲面

图7 仿真结果
从图7 可以看出,相对于传统PID 控制器而言,改进的模糊PID 控制器在超调量和系统的稳定性方面都有很大改善,且响应时间更短。改进的PID 控制器可以对雷达伺服系统的控制起到良好效果,相对于传统的PID 调节,这种控制方法能够更加快速、稳定地响应伺服系统的设定。
为了更准确反映改进的模糊PID 控制器在更加复杂系统下的效果,在原有仿真模型的基础上分别加入噪声干扰及饱和区的非线性影响因素。
首先,在系统加入了白噪声的干扰因素,如图8 所示。在传统的PID 控制和改进的模糊PID 控制下的输出结果都产生了一定的波动性,但改进的模糊PID 控制器在噪声环境中能更加快速地趋于稳定状态,具有良好的处理复杂环境的能力。

图8 加入噪声后的仿真结果
其次,在系统的输出部分加入了如图9 所示的死区和饱和区的非线性影响因素,从而得到在PID控制和改进的模糊PID 控制下系统的输出信号,如图10 所示。
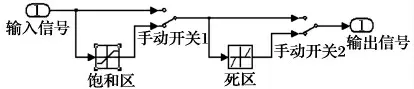
图9 死区和饱和信号
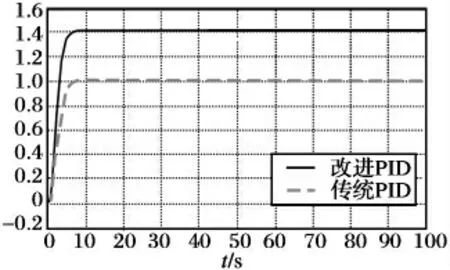
图10 加入饱和区后的仿真结果
由图10 可知,在系统控制输入加入非线性干扰后,改进的模糊PID 控制器能够较好地抑制系统非线性因素,而传统的PID 控制器此时已失真发散,控制性能严重下降。
6 结 论
在雷达伺服系统设计中,传统PID 控制器在解决实际非线性及复杂情况的问题上遇到困难,因此改进的PID 控制器是十分必要的。本文考虑利用遗传算法、S-T 模糊逻辑控制以及径向基函数神经网络相结合的方法来改进PID 控制器的最优参数,并将整定的参数结果运用在雷达伺服系统PID 控制器的设计上。改进的PID 控制器易于实施、稳定性高、收敛性强,计算效率也得以提高,使系统误差接近于零。通过simulink 进行仿真并与传统雷达伺服系统PID 控制器进行比较,实验结果表明,改进的PID 控制器收敛速度更快,计算效率更高,超调误差更小,对非线性因素控制效果更好并且解决了误差难以接近于零的问题。所以改进的雷达伺服系统PID 控制器在实际应用中具有一定的优势,是可行有效的。
[1]俞庭国. 模糊PID 控制技术在雷达伺服系统中的应用研究[D]. 重庆:重庆大学,2005.
[2]吴娟,孙娟萍,刘辉,等.自校正PID 控制在雷达天线控制系统中的应用[J]. 自动化仪表,2009,7:69-71.
[3]曹承志,王楠. 智能技术[M]. 北京:清华大学出版社,2004.
[4]启宏杰,尔联洁,刘强,等.基于神经网络自适应稳定PID 控制方法的研究[J]. 北京航空航天大学学报,2001,27(2):153-156.
[5]Visioli A. A New Design for a PID Plus Feedforward Controller[J]. Journal of Process Control,2004,14(4):457-463.
[6]刘志远,吕剑虹,陈来九. 智能PID 控制器在电厂热工过程控制中的应用前景[J]. 中国电机工程学报,2002,22(8):128-134.
[7]董学平,徐本连. 基于混杂系统的智能PID 控制设计[J]. 合肥工业大学学报(自然科学版),2004,8:960-963.
[8]刘金琨.先进PID 控制MATLAB 仿真[M]. 北京:电子工业出版社,2011.
[9]韦巍,何衍.智能控制基础[M]. 北京:清华大学出版社,2008.
[10]Al Gizi A J H,Mustafa M W,Jebur H H. A Novel Design of High-Sensitive Fuzzy PID Controller[J]. Applied Soft Computing,2014,24:794-805.
[11]刘昆,颜钢锋. 基于模糊RBF 神经网络的函数逼近[J]. 计算机工程,2001,24(2):70-73.
[12]张国忠. 智能控制系统及应用[M]. 北京:中国电力出版社,2007.
[13]朱卫华,陆荣双,杨文龙. 采用遗传算法优化的模糊控制系统[J].兵工自动化,2006,25(8):60-61.
[14]韩瑞峰. 遗传算法原理与应用实例[M]. 北京:兵器工业出版社,2010.
[15]李红利,张晓彤,兰立柱,等.基于遗传算法的RBF神经网络的优化设计方法[J]. 计算机仿真,2003,20(11):67-69.
[16]Liu Yaolun,Tong Chiachang,Jwo Wushun,et al. Design an Intelligent Neural-Fuzzy Controller for Hybrid Motorcycle[C]// Fuzzy Information Processing Society,Annual Meeting of the North American,2007:283-288.

