拦截跳跃式机动目标的制导律设计

惠耀洛，南 英，赵华超

(1. 南京航空航天大学 航天学院，南京 210016;2. 中国空空导弹研究院，河南 洛阳 471009)

0 引 言

随着临近空间［1］概念的提出和临近空间飞行器［2－3］不断取得技术上的突破，未来的战争将是海、陆、空、天一体化的战争。采用助推－滑翔飞行方案的高超声速临近空间飞行器，可大幅节省燃料，同时跳跃式机动弹道能够显著提高突防能力，这种弹道被称为桑格尔弹道［4］。由于采用桑格尔弹道的临近空间飞行器具有高速、大机动特性，给一般拦截弹的拦截提出了挑战。本文针对这种临近空间飞行器设计了轨控式直/气复合拦截弹的三维滑模变结构制导律。

有关拦截弹的制导律研究，文献［5－6］分别引入预测交班点和预测拦截点的概念设计中制导律，由于临近空间飞行器作高速跳跃机动，采用预测制导技术将会造成较大误差，导致拦截失败。文献［7］基于状态相关Riccati 方程设计了最优滑模制导律，在已知目标最大机动加速度的情况下，该制导律能够对机动目标具有良好的鲁棒性。文献［8］采用Takagi-Sugeno 线性模糊模型描述弹－目相对运动方程，并用非线性模糊H∞制导律消除误差和外界干扰的影响，然后采用线性矩阵不等式技术设计了考虑控制约束的H∞最优制导律。文献［9］采用最优控制理论，以最小化控制能量和中末交班时刻速度前置角作为性能指标设计拦截机动目标的中制导律。由于导弹动力学模型的高度非线性，发动机和气动力的存在增加了其复杂度，使得两点边值问题的求解无法在弹上实时完成。文献［10］采用卡尔曼滤波器对蛇形机动目标特性进行在线估计，推导了最优数值制导律。由于卡尔曼滤波技术算法复杂，且需要精确知道系统模型和噪声统计特性，不利于在导弹攻防对抗过程中使用。文献［11］在修正极坐标系中采用滑模变结构控制理论设计了对蛇形机动目标的制导算法。文献［12］在三维最优制导律的基础上，加入与目标加速度成比例的修正项以拦截大机动目标，但在弹－目对抗过程中，不易获得目标加速度。

本文首先建立了视线坐标系中的三维弹－目相对运动方程，设计了随目标跳跃幅度和弹－目距离自适应变化的滑模趋近律，推导了三维滑模制导律，然后采用轨控直接力控制技术，给出了直接力/气动力的分配方案。以某型临近空间飞行器为拦截目标，进行弹－目攻防对抗飞行仿真，大量仿真结果表明，该制导律与控制策略能够使拦截弹精确命中高速、大机动临近空间飞行器等目标。

1 数学模型

图1 所示为视线坐标系与地面坐标系的转换关系，视线坐标系的原点O 取在导弹的瞬时质心上，OXL轴与弹－目视线方向重合，指向目标;OYL轴位于包含弹－目视线的铅垂面内垂直于OXL轴，指向上为正;OZL轴垂直于其他两轴并构成右手坐标系。qε为视线高低角，qβ为视线方位角。

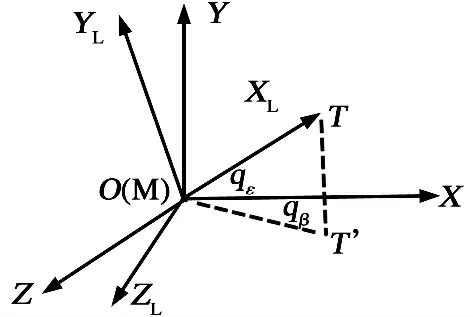
图1 视线坐标系与地面坐标系的转换关系

由地面坐标系OXYZ 到视线坐标系OXLYLZL的转换矩阵L 为

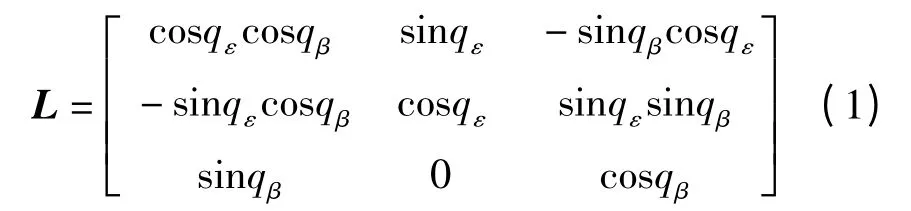
在视线坐标系中，建立弹－目相对运动方程［13］:

式中:

将导弹和目标的三维相对运动解耦为纵向平面内的运动和侧向平面内的运动，取R=Rxy，u=ayL，f=atyL，可得纵向平面内的弹－目相对运动方程;取atzL，可得侧向平面内的弹－目相对运动方程。其中:)和)分别为某一小时间区间Δt 内的视线高低角增量和视线方位角增量;Rxy和Rxz分别为弹－目距离在XOY 面和XOZ 面内的投影;u 为控制量;ayL和azL分别为导弹在OYL和OZL方向上的制导指令加速度;f 为干扰量;atyL和atzL分别为目标在OYL和OZL方向上的机动加速度。

2 拦截跳跃式机动目标的滑模变结构制导律设计

对于临近空间跳跃式机动目标，由于其弹道波动没有规律，不能准确预测其落点位置，不宜采用常规的预测制导律，同时临近空间飞行器的突防机动能力较强，如果在中制导阶段就采用常规比例导引或其他制导律紧密跟踪目标轨迹进行相应机动，会使导弹耗能增加，不能完成中远程拦截任务。综合考虑上述两点约束条件，对临近空间跳跃式机动目标的拦截弹制导律设计，应该保证拦截弹既能跟踪目标机动，不丢失目标，又可控制拦截弹的弹道波动幅度，减小能耗。

为使导弹在末制导阶段以平直弹道拦截目标，要求x→0，即视线角增量为零，同时视线角增量变化率也为零。选择滑模面为

对于跳跃式机动目标，设计好滑模面之后，关键是要选择合适的滑模趋近律。滑模趋近律应该能够保证当目标跳跃幅度变化率较大时，放慢趋近速度，当目标跳跃幅度变化率较小时，加快趋近速度，这样可以在保证稳定跟踪目标的前提下，快速拦截目标。考虑上述条件，以纵向平面内的制导律设计为例，选取自适应滑模趋近律为

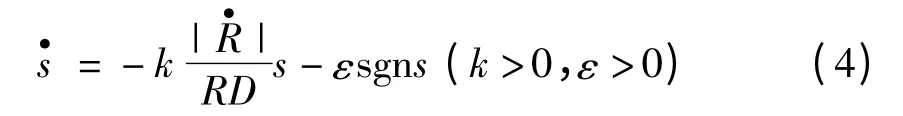
式中:

其中:D 为目标跳跃幅度变化率;τ 为对目标侦查的采样时间;yT1和yT2分别为前后两次侦查采样得到的目标飞行高度。上述滑模制导律的物理意义在于:当弹－目距离较远或者目标跳跃机动幅度较大时，减缓趋近速度;反之，加快趋近速度。

对式(3)求导，并将式(2)带入，得

由式(4)～(5)得到

由于滑模变结构系统自身具有抗干扰特性，可忽略目标机动加速度f，同时为了削弱抖动可以用高增益连续函数代替符号函数，得到

其中:δ 为小正数。

由Lyapunov 稳定性理论知系统渐进稳定。

因此，由式(5)得到导弹在视线坐标系下的制导指令加速度为

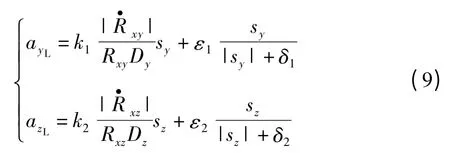
式中:ayL和azL分别为导弹在视线坐标系OYL和OZL方向上的制导指令加速度;sy和sz分别为在纵向和侧向平面内设计的滑模面;Dy和Dz分别为目标在纵向和侧向平面内的跳跃机动幅度变化率。

将视线坐标系下的制导指令转换到地面坐标系，得到

式中:ax，ay，az分别为导弹在地面坐标系三轴方向上的制导指令加速度。

3 轨控式直接力/气动力复合控制分配策略

由于临近空间飞行器在飞行末段仍具有较大的飞行速度和较强的机动能力，因此在拦截末段，需要采用直接力/气动力复合控制技术以提供拦截弹所需过载，提高拦截弹的机动能力和精确制导能力，达到对目标直接动能碰撞杀伤的拦截效果。

采用直接力控制技术的拦截弹主要依靠安装在导弹头尾部的微型姿控发动机或者安装在弹头质心侧面的轨控发动机来产生直接力，通过力矩(姿控方式)或力(轨控方式)的效果改变导弹姿态和轨迹，控制导弹飞行。侧向推力的产生方式一般有两种:一种是有公共燃烧室，通过几个喷管喷出的燃气流产生直接力;另一种是利用多个脉冲发动机产生直接力，脉冲发动机的推力是不可调的。

本文所设计的拦截弹采用具有公共燃烧室的轨控直接力装置。为提高轨控发动机的利用效率，减小拦截弹的能量消耗，仅在末制导阶段采用直接力/气动力复合控制方案，且在升力或侧向力不足以提供导弹所需机动过载时，轨控直接力发动机工作，提供拦截弹额外所需过载。直接力/气动力复合控制框图如图2 所示。

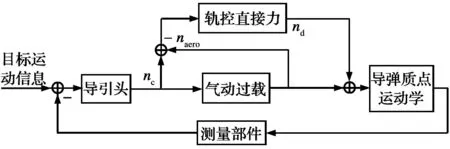
图2 直接力/气动力复合控制框图

当导弹开始进入末制导阶段，即当弹－目距离小于导引头最大探测距离Rd时，开启直接力/气动力复合控制系统。当制导指令nc超过气动力提供的最大过载值nam，由轨控直接力补充提供导弹所需机动过载。naero为导弹产生的气动过载值，naero和nam由气动数据插值得到，nd为采用过载指令分配策略得到轨控直接力需要提供的机动过载值，然后可由nd计算出所需轨控直接力装置提供的推力大小，nd计算公式如式(11)所示，其中nmax为直接力/气动力系统所能提供的最大机动过载值，ndmax为直接力单独作用时所能提供的最大过载值。

同时，为保证拦截弹末段能精确命中目标，使视线角速率快速收敛，因此导弹拦截末段采用经典比例导引，其具体形式可参阅文献［14］。设置导引律切换条件为R=Rd，则拦截导弹制导指令加速度可表示为

4 飞行对抗数值仿真与分析

以某型临近空间飞行器为拦截目标，通过弹道反设计技术得到临近空间飞行器的弹道数据。采用本文的制导与控制方法，进行导弹与目标的攻防对抗飞行仿真。设置导弹初始位置坐标(2 050，10，0)km，初始速度500 m/s，采用二级发动机技术;设置目标初始位置(0，0，0)km，初始速度为0 m/s，假设载机距离临近空间飞行器1 500 km 时开始发射导弹。设置制导律参数:k1=5，k2=0.002，ε1=10，ε2=10，δ1=0.01，δ2=0.01，τ =0.01 s，Rd=50 km，仿真结果如图3 ～15 所示。仿真结果分析:

图3 导弹和目标三维飞行轨迹

图4 导弹和目标飞行轨迹在铅垂面内和水平面内投影

图5 导弹推力与质量随飞行时间的变化

图6 导弹飞行速度

图7 目标飞行速度

图8 目标轨迹倾角和偏航角

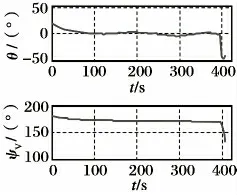
图9 导弹轨迹倾角和偏航角

图10 视线高低角和视线方位角

图11 视线高低角和视线方位角角速率

图12 导弹和目标距离变化率和距离值

图13 导弹法向和侧向过载

图14 导弹气动力过载

图15 导弹轨控直接力

(1)由图3 ～4 知，临近空间飞行器目标在铅垂面内发射后迅速爬升至70 km 高度，之后进入程序制导阶段，在铅垂面内做跳跃机动，同时在水平面内也做机动飞行。导弹捕获目标信息后，跟踪目标轨迹飞行，弹道较为平直，波动起伏小，在目标下压攻击段将其成功拦截，拦截点高度约为10 km。

(2)由图5 ～6 知，拦截弹采用二级发动机技术，一级发动机比冲为315.3 s，工作时间为88 s，二级发动机比冲为238 s，工作时间为23 s，拦截弹经两次加速后达到最大速度约12Ma。

(3)由图7 ～8 知，临近空间飞行器目标同样采用二级发动机技术，最大飞行速度约8Ma，在飞行约400 s 时被导弹捕获，最终在飞行约805 s 后被导弹拦截。目标轨迹倾角在－90°～90°之间变化，其中跳跃机动段轨迹倾角在－20°～20°之间变化。

(4)由图9 ～15 知，导弹在整个飞行过程中法向过载和侧向过载均较小，视线角的变化幅度和变化率也较小，弹道比较平直。仅在飞行末段，由于目标迅速下压机动，导弹所需机动过载迅速增加，视线角和弹道角都有明显变化，在导弹气动力不足以提供导弹所需机动过载时，轨控发动机工作，提供最大的轨控直接力约为20 kN，采用直接力/气动力复合控制技术控制导弹精确命中目标。

5 结 论

基于滑模变结构理论，本文设计了随目标跳跃幅度变化率和弹－目距离自适应变化的滑模趋近律，推导了三维平面内的拦截弹滑模变结构制导律。采用轨控直接力控制技术，给出了直接力/气动力的分配方案。以一高超音速跳跃式机动突防临近空间飞行器为拦截目标，进行弹－目攻防对抗飞行仿真，飞行对抗仿真结果表明，该制导律与控制策略能够使拦截弹精确命中高速、大机动临近空间飞行器等突防目标，同时拦截弹的弹道平缓，需用过载和能量消耗均较小。

［1］Hampton S. Near-Space［J］. Air Force Magazine，2005，88(7):36－40.

［2］McClinton C R，Rausch V L，Shaw R J，et al. Hyper-X:Foundation for Future Hypersonic Launch Vehicles［J］.Acta Astronautica，2005，57(2－8):614－622.

［3］Boudreau A H. Status of the U.S.Air Force HyTech Progam［R］. AIAA 2003－6947，2003.

［4］李建林. 临近空间高超声速飞行器发展研究［M］. 北京:中国宇航出版社，2012.

［5］董朝阳，周雨. 一种交班时刻性能最优的中制导律设计与仿真［J］. 系统仿真学报，2009，21(24):7873－7878.

［6］赵永涛，邱峻，胡云安. 一种利于交班的舰空导弹最优中制导律设计［J］. 海军航空工程学院学报，2013，28(3):246－252.

［7］Moosapour S S，Alizadeh G，Khanmohammadi S，et al. A Novel Nonlinear Robust Guidance Law Design Based on SDRE Technique［J］. International Journal of Aeronautical and Space Sciences，2012，13(3):368－376.

［8］Chen Borsen，Chen Yungyue，Lin Chunliang. Nonlinear Fuzzy H∞Guidance Law with Saturation of Actuators against Maneuvering Targets［J］. IEEE Transactions on Control Systems Technology，2002，10(6):769－779.

［9］周池军，雷虎民，叶继坤. 一种拦截机动目标的最优中制导律设计［J］.弹道学报，2012，24(3):49－53.

［10］刁兆师，李海田，单家元. 拦截蛇形机动目标考虑自动驾驶仪动态特性的最优制导律［J］. 北京理工大学学报，2013，33(3):229－234.

［11］田宏亮，梁晓庚，贾晓洪. 攻击大机动目标的变结构末制导律设计［J］. 计算机仿真，2011，28(10):70－72.

［12］徐鸣，吴庆宪，姜长生. 空空导弹攻击机动目标的三维最优制导律研究［J］.航空兵器，2005(6):7－12.

［13］周荻. 寻的导弹新型导引规律［M］. 北京:国防工业出版社，2002.

［14］钱杏芳，林瑞雄，赵亚男. 导弹飞行力学［M］. 北京:北京理工大学出版社，2000.