用于级联型大功率变流器的多变量组合控制方案

曹剑坤 谢少军

（南京航空航天大学自动化学院 南京 210016）

1 引言

由于受到高压大电流功率器件电压电流应力、发热密度、开关损耗以及性价比的限制，并为降低电磁干扰，大功率变流器常采用多模块级联的拓扑方案和低开关频率的控制方案[1-4]。多模块级联的拓扑方案中各模块的控制相对独立，组合方式灵活[5-8]。以较低的开关频率实现级联型大功率变流器的控制可以提高其效率和工作可靠性，但开关频率的降低会增加输出波形中不易被滤除的低次谐波含量，从而降低了输出波形质量。提高低开关频率工作时的输出波形质量，尤其是减小其中低次谐波含量是级联型大功率变流器的重要研究课题。

已有大量文献研究了可提高输出波形质量的低开关频率变流器方案。一类为间接的低次谐波消除方案，通过提高输出电平数量或等效开关频率以减小输出波形中的低次谐波含量。非对称直流母线电压的变流器[9-11]中各模块直流输入电压幅值按比例递增，在不改变原有电路结构的基础上提高输出电平数量，但输出电压幅值不易调节。载波移相PWM控制方案中输出电压的等效开关频率随逆变模块数量增加而增加，但对低次谐波的消除效果较差。另一类为直接的低次谐波消除方案。文献[12,13]基于谐波消除方案的特定谐波消除脉宽调制（SHEPWM）技术和特定谐波削弱脉宽调制（SHMPWM）技术实现了基波开关频率下多模块变流器输出低次谐波的直接消除，但该方案对低次谐波消除的数量有限并且开关角度的计算较复杂。文献[14]根据谐波抵消原理采用多模块阶梯波合成方案，各模块的输出电压经过合成变压器的移相和比例控制后，合成的输出电压中较多的低次谐波可直接被消除，但笨重的低频合成变压器增大了变流器的体积和损耗。此外，还有一类混合控制方案[15,16]将多模块变流器中用于主功率变换的模块工作于低频，用于提高输出波形质量的模块工作于高频，可得到接近正弦的电压波形输出。但混合控制方案中的高频工作模块开关损耗较大，同时也存在较大的电磁干扰。以上变流器方案在解决低开关频率下输出低次谐波问题时所付出的代价较大，级联型大功率变流器的优化控制需要在借鉴上述方案优势的基础上提出新的思路。

本文基于非对称级联型变流器拓扑，结合谐波抵消原理，提出一种用于级联型大功率变流器的多控制变量组合控制方案。该控制思路是将级联型多模块变流器中的各模块输出电压幅值、移相角度和脉冲宽度进行综合控制，提高低开关频率工作时的输出波形质量。该控制方案无需输出合成变压器即可直接消除较多的输出侧低次谐波，功率器件均可低频工作，控制方案简洁可靠，具有较强的通用性。

2 多变量组合控制方案及其特性分析

2.1 双变量组合控制及其输出电压谐波分析

本节首先分析各逆变模块输出电压幅值和移相角度两个变量的组合控制，即各级联逆变模块的直流母线电压比例和输出电压移相组合控制。

图1a示出了N+1（N为偶数）个级联逆变模块的输出电压波形。每个模块的输出是脉冲宽度固定为θ的准方波或方波，变流器输出相电压由N+1个逆变模块的输出电压移相叠加构成。控制直流母线电压可调节输出方波的幅值，输出电压移相可调节各模块输出电压的相位。图 1b示出了对应各模块输出电压的矢量图，图中第N+1个模块的输出电压矢量位于x轴，其他N个模块的输出电压矢量关于x轴对称。

图1 调幅与移相组合控制方案原理示意图Fig.1 Principal of control scheme

单相输出电压的傅里叶分解表达式为

式中，Udc_q和φq分别为第q个逆变模块的输入直流母线电压和输出电压移相角。

由于模块输出电压关于x轴对称，式（1）可简化为

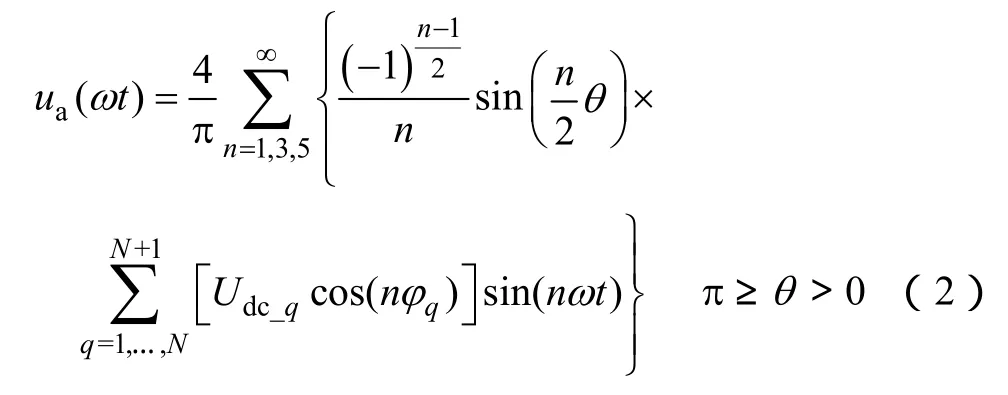
当Udc_q和φq满足式（3）时，可以消除输出电压中的n次谐波。

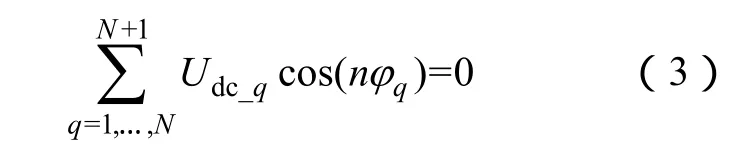
控制变量Udc_q和φq可根据以下 2个条件进行取值：①应用于单相变流器时，被消除的谐波次数应从输出侧中最低次谐波开始选取，如3、5、7、…；应用于三相变流器时，输出线电压中的零序分量可自行抵消，被消除的谐波次数应从输出侧中非零序的最低次谐波开始选取，如5、7、11、…。可消除的谐波数是由逆变模块数量决定的；②由谐波消除方程（式（3））进一步推导得

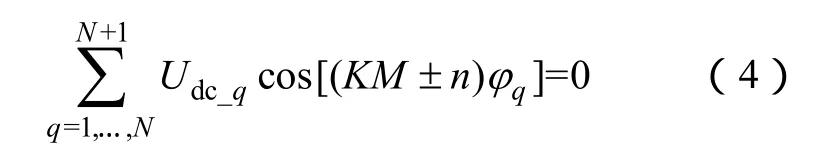
式中，φq是以移相角φ为公差的等差数列；M=2π/φ为输出相电压的阶梯数量；K为正整数。

由此可见，在对各模块输出电压相位施加约束后，除了消除输出侧的n次谐波外，还消除了KM±n次谐波。

以N=2为例，3个逆变模块级联的输出相电压阶梯数M=12，则移相角公差φ=2π/M=30°，控制变量φ1=30°、φ2=-30°、φ3=0°。由于 3个电压矢量的对称关系，所以Udc_1=Udc_2，仅有一个电压比例关系Udc_3:Udc_1需要求解，可消除 5次谐波。根据式（3）解得控制变量Udc_1:Udc_2:Udc_3=1:1:。同时，根据式（4），在消除5次谐波时，12K±5次谐波同时被消除。

下表列出了将该控制方案应用于三相变流器时，主要控制变量取值、输出特性与级联模块数量的关系。通过对直流母线电压Udc_q的比例控制和输出电压移相角φq的相位控制，在功率器件开关频率仅为输出电压基波频率时，输出线电压中仅剩余6(N/2+1)K±1次谐波。输出线电压中剩余的高次谐波可以通过体积重量较小的滤波器滤除。

在保证各模块直流母线电压幅值Udc_q的相对比值不变条件下，对各模块控制变量Udc_q进行等比例调节，可调节基波输出电压幅值。采用此调节方式不影响控制方案中的谐波消除特性。

表 谐波消除控制的主要参数Tab. Main parameters of harmonic eliminate control

该控制方案发挥了多模块级联型变流器控制方式灵活的优势，在大功率场合应用具有以下特点：①全部功率器件均为低开关频率工作，可提高变流器效率；②直接消除输出侧的大量低频谐波，可提高输出波形质量；③无需特殊的低频合成变压器，可减小变流器体积重量。

2.2 结合PWM调制的多变量组合控制特性分析

由式（1）可见，调节各逆变模块统一的脉冲宽度θ可对基波输出电压幅值进行调节。定义单脉冲宽度调制下调制比m为

由式（2）可见，基波输出电压正比于调制比m，改变调制比m不会影响控制方案的谐波消除特性。

为获得比单脉宽调制更加优质的输出波形和更快的系统响应速度，在双变量组合控制的基础上，可加入低频的脉冲宽度调制（PWM）进行脉冲宽度变量控制，形成三控制变量的组合控制方案。需要指出的是，加入低频 PWM调制不得影响双变量组合控制的低次谐波消除特性。下面分别分析以单极性和双极性PWM调制策略作为脉冲宽度变量与之前所述双控制变量的结合控制。

以逆变模块q为例，单极性PWM调制策略和双极性 PWM调制策略下的输出电压波形分别如图2a和图2b所示。图中的调制波为1/4周期对称，θ1～θy为中心对称的脉冲宽度，调制波幅值为Udc_q。

图2 PWM调制下逆变模块q的输出波形Fig.2 Output voltage waveforms of inverter moduleqwith PWM modulation

各逆变模块的单极性 PWM 调制波与图 2a相同，结合图1的双控制变量方案进行模块间的移相角度和幅值比例控制，形成三控制变量的组合控制方案。总输出电压为各逆变模块输出电压的叠加，其傅里叶分解表达式为

式（6）与式（2）的单脉冲波形傅里叶分解表达式相比，仅改变了调制比表达式部分

由于调制比m1与式（6）中谐波消除方程为乘积的关系，各逆变模块统一的单极性 PWM调制策略不影响低次谐波的消除特性。

同理，各逆变模块均为双极性PWM调制时总输出电压的傅里叶分解表达式为

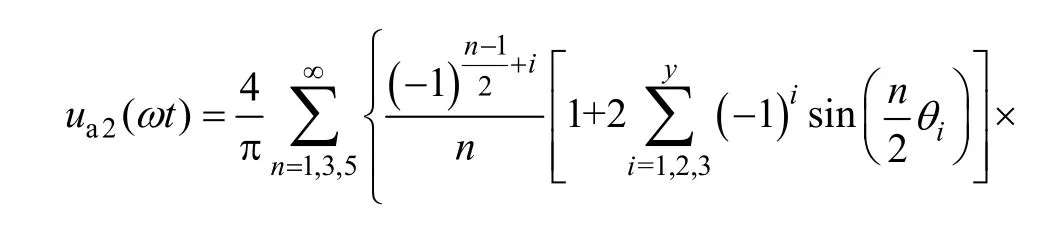
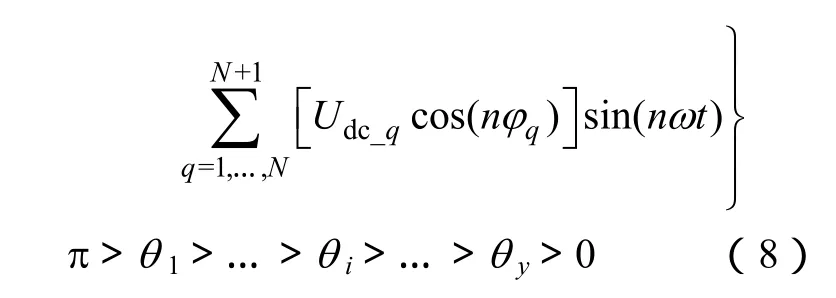
式中，双极性调制下的调制比m2为

各逆变模块统一的双极性PWM调制策略同样不影响低次谐波的消除特性。

理论上，无论是单极性还是双极性 PWM调制波形，均可等效为准方波或方波电压以半波对称方式正负叠加而成。所以，各逆变模块的输出 PWM波形均为半波对称奇函数，统一的 PWM调制策略仅对称地改变输出脉冲宽度的分布，不影响控制方案的低次谐波消除效果。

由以上分析可知，对各变流模块输出电压幅值、移相角度和脉冲宽度等多控制变量进行组合的控制方案可在全部功率器件低开关频率工作条件下实现低次谐波含量较少的输出波形。非对称直流母线电压控制、阶梯波移相角度控制以及单极性或双极性PWM 调制策略的融合，可有效提高级联型多模块变流器的输出特性。

2.3 逆变模块的功率分配

多模块级联型变流器中各逆变模块的输出端串联，其输出电流相同，并且各模块在统一的调制比下工作。假设各逆变模块的传输效率相同，其视在功率比仅与输出电压相关。各逆变模块的有功功率与输出电压幅值和移相角度相关。

假设输出电流为相位滞后输出电压α、有效值为I的正弦波，各逆变模块的传输效率为100%，输出波形如图1a所示。由图1b结合式（2）可得，逆变模块q的视在功率Sq和有功功率Pq分别为

式中，调制比m在单极性PWM调制下为m1，在双极性PWM调制下为m2。

根据式（10），N+1个逆变模块的视在功率比值为Udc_1:…:Udc_N:Udc_N+1，有功功率比值为Udc_1cos(φ1—α):…:Udc_Ncos(φN—α):Udc_N+1cos(φN+1—α)。各逆变模块的视在功率比仅与各自直流输入电压幅值相关，各逆变模块的有功功率比仅与各自直流输入电压幅值和输出电压移相角度相关。虽然各模块功率与调制比相关，但功率比与调制比无关。

2.4 与传统控制策略的对比仿真及分析

在大功率变流器的低开关频率控制方案中，比较常用的两种是多模块的载波移相 PWM控制以及多模块的 SHEPWM控制。下面将多变量组合控制方案与以上两种控制方案进行对比仿真及分析。控制方案的仿真分析中，每相逆变模块数量均为3，功率器件的开关频率为基波频率。滤波器采用 LC型，截止频率为9倍基波频率。

多模块的载波移相PWM控制中，各模块的直流母线电压相同，均采用单极性调制，调制波选用正弦波，载波移相角度为60°。

多模块的 SHEPWM控制中，各模块的直流母线电压相同，均采用 1/4周期对称的单极性调制。每个逆变模块包含1个开关角度变量，可在调节基波电压幅值的同时消除2个低频谐波。由于输出电压为半波对称函数，无偶次谐波，并且三相对称逆变器的输出波形中零序分量可自行抵消，该控制方案消除的特定低次谐波为5次和7次。

在基波开关频率条件下，对比分析本文提出的多变量组合控制方案与以上两种控制。在调制比m=m1=0.8时，三种控制方案下滤波前和滤波后输出线电压前50次的各次谐波含量百分比以及THD对比如图3所示。

图3 三种控制方案对应的输出谐波对比Fig.3 Comparison of output harmonics under three kinds of control schemes

通过对比分析可得：①载波移相PWM控制方案的输出线电压 THD最高，并且谐波分布在低频区域，滤波后低频谐波含量较高；②SHEPWM控制方案中的输出线电压THD最低，最低次谐波为11次，低频谐波含量少且分布较平均，滤波效果显著。但是，其开关角度的求解过程复杂，一般需离线计算，并且所得开关角度数据根据调节精度的增加而线性增加，占用较多的存储空间。各逆变模块的功率分配随调制比变化；③多变量组合控制方案的输出线电压THD较低，最低次谐波同样为11次，输出谐波个数少且频率分布集中，利于滤波器和波形优化方案的设计。与 SHEPWM控制方案相比，该方案无需开关角度的离线计算，通过调节脉冲宽度θ可进行输出电压基波幅值的连续调节，控制方式简洁，无需开关角度存储空间；④多变量组合控制方案的滤波后输出线电压中主要谐波成分为11次和13次谐波。该方案如结合 SHEPWM技术，仅需少量开关角度计算即可显著提高输出电压波形质量。

3 控制方案的通用性分析

前面提出的多控制变量组合控制方案可用于不同的单相多模块级联型变流器拓扑，也可经过移相组合应用于三相多模块级联型变流器。下面分析该控制方案在 3种典型的多模块级联型拓扑中的应用，阐述该控制方案的通用性。

H桥级联型三相变流器拓扑[2]中，每相变流器由N+1个H桥逆变模块级联构成，是最常用的级联型拓扑，具有模块化程度高、可靠性高、易于控制等特点。每个逆变模块均需独立的直流电源。

多变量组合控制方案用于H桥级联型拓扑时，以A相为例，图1b的N+1电压矢量对应该相N+1个逆变模块的输出电压。非对称的直流母线电压各模块独立的输入电压源得到、相位调节以及 PWM调制策略均可通过控制各H桥逆变模块中开关管的开关时序实现。该方案可广泛应用于中频电源、变频传动等领域。

混合非对称型三相变流器拓扑[8,15]中的每个逆变模块可选用不同的变流器拓扑，本文以常用的H桥拓扑与二极管钳位型三电平拓扑结合为例。该结构由N个H桥拓扑和1个共用的二极管钳位型三相三电平拓扑级联构成，与H桥级联型拓扑相比减少了独立的直流电源个数。

多变量组合控制方案用于混合非对称型拓扑时，以A相为例，该相N+1个逆变模块的输出电压可分别对应图1b中N+1个输出电压矢量。多变量的调节方式与应用于H桥级联型拓扑时相同。该方案适用于大功率的变频传动场合。

基于模块化多电平变换器（MMC）方案的三相变流器拓扑[2]中，每相的上桥臂和下桥臂均由N+1个斩波模块构成。

多变量组合控制方案用于基于MMC方案的拓扑时，以A相为例，需从该相上桥臂和下桥臂各选出一个斩波模块构成一对，当两者电容电压幅值相同，输出电压相位相差 180°时，两者可合成图 1b中的一个输出电压矢量。以此类推，N+1对斩波模块可合成N+1个输出电压矢量。控制方案中的每个电压矢量即与每对斩波模块相对应，多控制变量的调节可通过控制每对斩波模块中开关管的开关时序实现。该方案应用于MMC拓扑时的难点在于，实现中低开关频率条件下斩波模块内电容电压的比例控制。该方案模块化程度高，斩波模块内器件少，直流输入侧仅需一个电源，在高压直流输电（HVDC）领域有较好的应用。

4 仿真和实验结果

为验证多变量组合控制方案的可行性，本文搭建了仿真平台和实验平台进行原理验证。

仿真平台采用Matlab/Simulink软件搭建，拓扑选用图5所示的混合非对称级联型结构，其中N=2。三相三电平逆变模块的输入端采用三相电网（380V/50Hz）直接整流滤波后获得，其他6个逆变模块的独立电源经隔离变压器组整流滤波后得到，隔离变压器组的匝比关系由控制方案中输出电压幅值比例关系决定。

将多变量组合控制结合单极性 SHEPWM调制后进行仿真，输出电压基波频率f0=50Hz，功率器件的开关频率为fshe=3f0=150Hz。LC滤波器参数为：Lf=5.4mH、Cf=23μF，负载为R=19Ω。脉冲宽度θ1～θ3由特定谐波消除算法得到，可使输出电压中的11次和13次低频谐波被消除。图 4a为调制比mshe=m1=0.9的滤波前输出线电压以及线电压FFT分析频谱图。如图所示，输出线电压中的5次、12K±5次谐波以及 11次、13次谐波均被消除。在三相对称时，输出线电压中的零序分量相互抵消，仅包含12(K+1)±1次谐波，最低次谐波为23次。图4b为在该调制策略和调制比下滤波后的输出相电压波形及其FFT分析频谱图。由于11和13次低频谐波进一步被消除，滤波器对输出谐波抑制效果较好，滤波后相电压的正弦度很高。频谱图中少量低次谐波的出现是由于采用不控整流电路时，输出的直流母线电压中包含少量低频电压脉动。该低次谐波对输出波形质量以及总谐波失真（THD）的影响很小。

图4 结合SHEPWM调制策略的仿真波形Fig.4 Simulation waveforms with SHEPWM strategy

实验样机的拓扑与仿真所用的相同。各模块输入电压的幅值按比例减小，三相三电平逆变模块的输入侧电压为104V，其他6个逆变模块的输入侧电压均为 30V。实验样机的输出电压基波频率f0=50Hz，输出电压幅值根据调制比可调节。级联型三相变流器的模块数量较多，无法直接由DSP提供驱动信号，可采用DSP与FPGA相结合实现控制和保护。DSP实现数据存储、数据采样、保护以及功率器件开关角度的计算功能；FPGA通过数据锁存和脉冲信号移相得到每个逆变模块功率器件的驱动信号。变流器可以采用三相统一控制，也可以每相采用各自独立的单电压闭环控制。图5所示为各相单独控制时的A相变流器控制框图。

图5 单电压闭环控制实现框图Fig.5 Block diagram of single voltage closed loop control

图 6a为各逆变模块在基波开关频率下采用多变量组合控制，每相逆变模块数量为 3，脉冲宽度θ=130°时，三相输出线电压实验波形以及线电压FFT频谱图。如图所示，输出线电压中的5次、12K±5次谐波均被消除，零序分量也相互抵消。在全部功率器件均以基波开关频率工作时，输出线电压中仅包含12K±1次谐波。

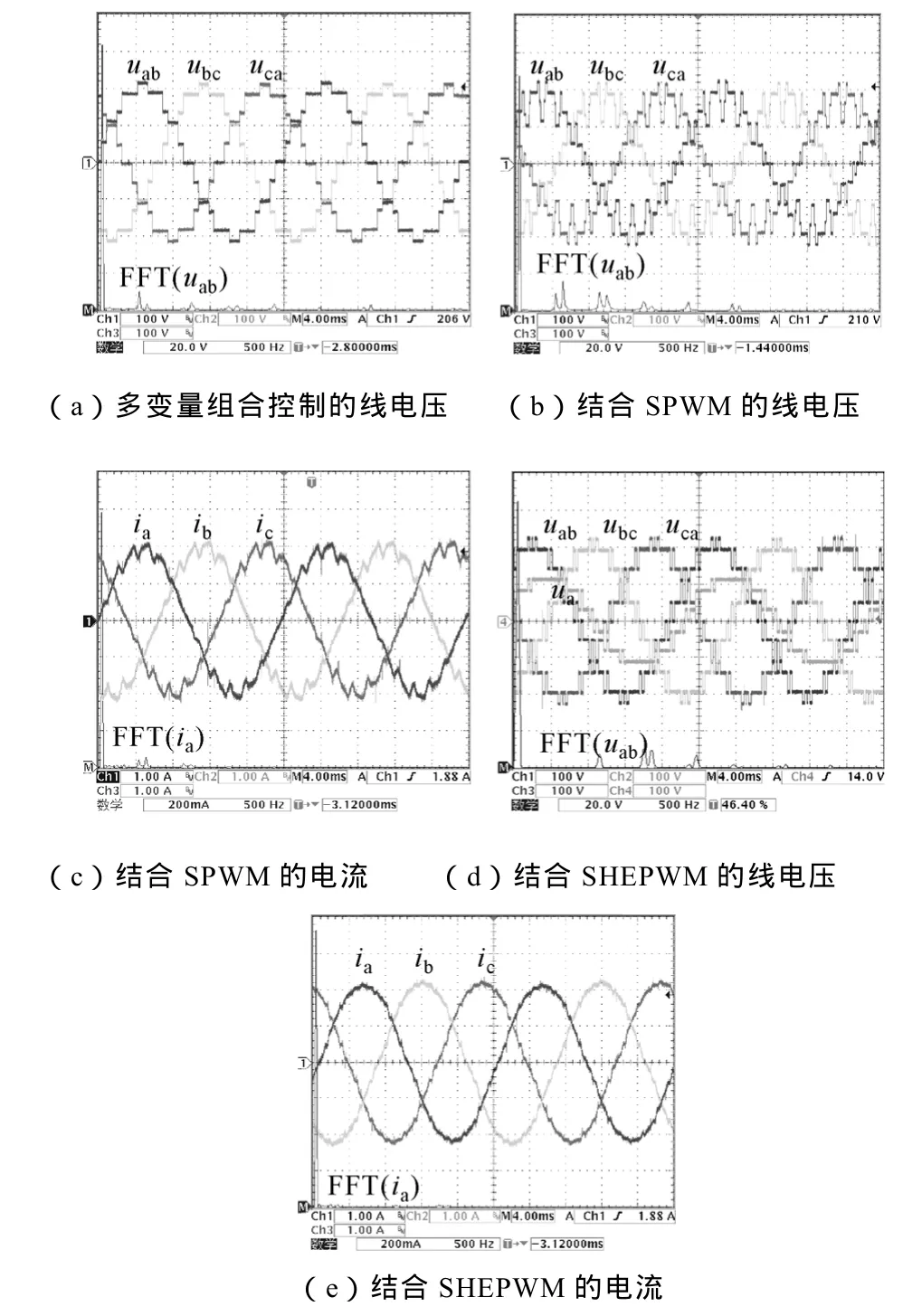
图6 实验波形及FFT分析Fig.6 Experimental waveforms and FFT analysis

将多变量组合控制方案分别结合单极性SPWM策略和SHEPWM策略进行实验，功率器件的开关频率fs=3f0=150Hz。三相负载对称，均为R=50Ω、L=25mH。各模块输出电压波形如图2a所示，图中y=3。结合 SPWM策略的脉冲宽度θ1～θ3由载波交截得到，结合 SHEPWM 策略的脉冲宽度θ1～θ3与仿真分析相同。图6b为结合单极性SPWM策略下调制比ms=4m1/π=1时，三相输出线电压波形以及线电压 FFT频谱图。输出线电压基波幅值可根据ms调节，其波形中仅包含12K±1次谐波。图6c为在该调制策略和调制比下对应三相输出电流波形及其FFT分析频谱图。图6d为结合单极性SHEPWM策略下调制比mshe=m1=0.9的三相输出线电压和A相相电压实验波形以及线电压FFT分析频谱图。与仿真波形的分析相同，三相输出线电压中仅包含12(K+1)±1次谐波，最低次谐波为23次。图6e为在该调制策略和调制比下对应三相输出电流波形及其FFT分析频谱图。两者相比，结合SHEPWM策略的多变量组合控制方案的输出波形中低次谐波含量更少，11次和13次谐波被消除后输出电流波形的正弦度很高。

图7对比了单极性SPWM和SHEPWM作为脉冲宽度调制策略时，宽调制比范围内输出相电压、线电压和电流的THD。在较宽的调制比区间，两者的输出波形 THD均可保持在较低数值，SHEPWM调制策略下的输出波形THD比SPWM调制策略下的更低，输出波形质量更高。

图7 宽调制比下的输出电压和电流THDFig.7 Output voltage and current THDs within wide modulation ratios

5 结论

由于模块化结构的变流器中各模块的控制方式以及输出特性可相对独立控制，各模块输出波形的幅值比例、相位及其脉宽调制策略等均可作为控制变量进行控制。本文根据上述控制思路，提出了一种多变量组合控制方案，基于谐波抵消原理对上述控制变量进行优化组合。

多变量组合控制方案中所有逆变模块的功率器件均工作于低开关频率，具有优越的低频谐波消除和输出调节能力，具有较强的通用性，可应用于多种典型的多模块级联型变流器拓扑，在大功率的独立电源，如大容量中频电源、岸电电源、应急电源（EPS）等场合具有潜在的应用价值，并可以用于中、大功率的变频传动系统。

[1] Haitham Abu-Rub,Joachim Holtz,Jose Rodriguez,et al. Medium-voltage multilevel converters--state of the art,challenges,and requirements in industrial applications[J]. IEEE Transactions on Industrial Electronics,2010,57(8): 2581-2596.

[2] Mariusz Malinowski,K. Gopakumar,Jose Rodriguez,et al. A survey on cascaded multilevel inverters[J].IEEE Transactions on Industrial Electronics,2010,57(7): 2197-2206.

[3] 朱思国,陆佳政,欧阳红林,等. 基于谐波注入法的级联型逆变器谐波消除研究[J]. 电工技术学报,2012,27(8): 194-202.

Zhu Siguo,Lu Jiazheng,Ouyang Honglin,et al.Research of harmonic elimination based on harmonic injection for cascaded inverter[J]. Transactions of China Electrotechnical Society,2012,27(8): 194-202.

[4] 费万民,都小利,居荣,等. 基于等面积法的多电平逆变器 SPWM 方法[J]. 电工技术学报,2010,25(3): 89-96.

Fei Wanmin,Du Xiaoli,Ju Rong,et al. A novel PWM method for multilevel inverters[J]. Transactions of China Electrotechnical Society,2010,25(3): 89-96.

[5] Preethi G,Monika J Gayathri,Jamuna V. Digital Simulation of multicarrier PWM strategy for multilevel inverter[C]. International Conference on Computing,Electronics and Electrical Technologies,2012:509-514.

[6] Ahmad Mohammad,Khan B H. New approaches for harmonics reduction in solar inverters[C]. 2012 Students Conference on Engineering and Systems,2012: 1-6.

[7] 张颖,李崇坚,朱春毅,等. 三电平 H 桥级联型逆变器[J]. 电工技术学报,2011,26(5): 78-82．

Zhang Ying,Li Chongjian,Zhu Chunyi,et al. Threelevel H-bridge cascade type multi-level inverter[J].Transactions of China Electrotechnical Society,2011,26(5): 78-82.

[8] 曹剑坤,谢少军. 移相与 SHEPWM 结合控制的级联型混合非对称三相变流器[J]. 电工技术学报,2013,28(12): 290-296．

Cao Jiankun,Xie Shaojun. Multi-level hybrid asymmetric three-phase inverter with phase shift plus SHEPWM control scheme[J]. Transactions of China Electrotechnical Society,2013,28(12): 290-296.

[9] Samuel C S Kiruba,Ramani K. Multilevel inverter control for wind-photovoltaic generation systems[C].2012 International Conference on Computing,Electronics and Electrical Technologies,2012: 457-462.

[10] Batschauer A L,Mussa S A,Heldwein M L. Threephase hybrid multilevel inverter based on half-bridge modules[J]. IEEE Transactions on Industrial Electronics,2012,59(2): 668-678.

[11] Kiruthika C,Ambika T,Seyezhai R. Implementation of digital control strategy for asymmetric cascaded multilevel inverter[C]. 2012 International Conference on Computing,Electronics and Electrical Technologies,2012: 295-300.

[12] Jeevabharathi T,Padmathilagam V. Harmonic elimination of cascaded multilevel inverters using particle swarm optimization[C]. International Conference on Computing,Electronics and Electrical Technologies,2012: 301-306.

[13] Napoles J,Leon J I,Portillo R,et al. Selective harmonic mitigation technique for high-power converters[J].IEEE Transactions on Industrial Electronics,2010,57(7): 2315-2323.

[14] 陈万,谢少军,李磊,等. 一种PWM结合移相控制的低开关频率逆变器[J]. 中国电机工程学报,2012,32(18): 31-36.

Chen Wan,Xie Shaojun,Li Lei,et al. A low switching frequency inverter with PWM plus phase-shift control scheme[J]. Proceedings of the CSEE,2012,32(18):31-36.

[15] Sepahvand H,Khazraei M,Ferdowsi M,et al. A hybrid multilevel inverter with both staircase and PWM switching schemes[C]. IEEE Energy Conversion Congress and Exposition,2010: 4364-3467.

[16] Sepahvand H,Ferdowsi M,Corzine K A. A sevenlevel converter using a combination of staircase and PWM switching methods[C]. 36th Annual Conference on IEEE Industrial Electronics Society,2010: 2307-2310.