并网接口滤波器拓扑结构推演与分析

许德志 汪 飞 阮 毅 毛华龙 张 巍 杨 影

（上海大学机电工程与自动化学院 上海 200072）

1 引言

相比传统化石燃料发电，可再生能源的分布式发电具有用之不竭、清洁无污染等诸多优点，已经成为电力系统能源的重要组成部分。并网逆变器作为分布式发电系统与电网之间的关键接口设备，其性能好坏直接决定着并网电流质量，已经成为国内外研究的热点[1-4]。为抑制并网逆变器向电网注入高频谐波电流，需要在逆变器和电网之间接入滤波器，以保证入网电流总谐波畸变率和单次谐波含量均满足相关并网标准[5,6]。

由于滤波器的滤波特性与其拓扑结构密切相关，因此，研究滤波器拓扑结构对分析和控制并网逆变器具有重要的指导意义。传统电压源型并网滤波器一般采用单电感滤波，即L型滤波器。L型滤波器结构简单，增大滤波电感值可以减小并网电流谐波含量。然而随着并网逆变系统功率等级的不断增大（考虑到开关损耗，开关频率通常较低），为获得同样的滤波效果，太大的滤波电感值会使滤波器体积庞大和成本提高，而且也会影响系统的动态性能。为克服传统L型滤波器的缺点，有学者提出了LCL型并网滤波器[7]。相比L型滤波器，LCL型属于三阶滤波器，在高频段具有更强的谐波衰减能力，在相同总电感值情况下，LCL型滤波器在滤除高次谐波方面效果要明显好于L型滤波器[8,9]。为进一步降低滤波器的成本（或者在相同滤波器成本情况下实现更好的滤波效果），有学者在LCL型滤波器拓扑结构的基础上，考虑到逆变器脉冲宽度调制（Pulse Width Modulation，PWM）输出波形的频谱特点，提出了一种LLCL型并网滤波器[10]，该滤波器是在 LCL型滤波器电容支路上串联一个比其他两个滤波电感值小得多的电感（因而其成本和体积可以忽略），通过调整电感电容支路参数使支路串联谐振频率等于 PWM开关频率，即构成开关频率陷波器，极大地衰减逆变桥输出高频谐波中幅值最高、影响最大的开关频率次谐波成分，从而有效改善并网电流质量，同时也降低了滤波器成本和体积。

L型滤波器研究已经非常成熟，目前对并网接口滤波器的研究主要集中在LCL型和LLCL型滤波器参数设计和谐振阻尼方面[11-19]，关于不同滤波器拓扑结构对滤波性能影响的对比分析以及在此基础之上的新型拓扑结构探究，目前国内外均没有文献涉及。本文首先从滤波器拓扑结构角度入手，分析现有L型、LCL型及LLCL型滤波器的高频谐波衰减特性及拓扑结构特点。通过对不同拓扑滤波特性的比较和归纳，提出了一种并网接口滤波器统一电路模型。在此基础之上，对五阶以下滤波器结构进行了拓扑推演与特性分析，提出了 LLCCL1型和LLCCL2型两种新型并网接口滤波器拓扑结构。高阶滤波器（包括LLCL型）的使用会增加控制系统的复杂性和降低并网装置的可靠性，然而，与目前处于研究热点的并网滤波器混合无源阻尼技术[14,15]相比，其本质上都是对三阶 LCL滤波器在高频衰减效果、谐振抑制效果、滤波装置体积成本及控制系统稳定性等方面的不断改进，而且本文提出的滤波器统一电路模型从滤波器拓扑角度更加清晰地对上述诸方面的相互制约与性能折中进一步做了归纳和剖析，为新能源并网发电不同应用场合下并网接口滤波器拓扑结构或阻尼技术的选择提供了一定的理论支持。本文将所提滤波器与L型、LCL型及LLCL型滤波器在逆变器侧高频谐波衰减特性、电网侧高频谐波抑制能力、参数设计要求和谐振尖峰无源阻尼等方面做了详尽地分析与对比。最后通过仿真分析验证了本文所提两种新型滤波器结构以及比较研究结论的正确性和有效性，同时也证明了基于滤波器统一电路模型进行拓扑结构推演的合理性。

2 L型、LCL型和LLCL型滤波器特性分析

L型、LCL型和LLCL型滤波器拓扑结构分别如图 1a、图 1b和图 1c所示。图中，Linv为逆变器侧滤波电感，Lg为电网侧滤波电感，uinv为逆变器输出电压，ug为电网电压，iinv为逆变器侧电感电流，ig为并网电流，Cf为滤波电容，Lf为滤波电感，ih为高频谐波电流。为便于分析，L型滤波器在图中表示为Linv和Lg两电感的串联。从图中可以看出，LCL型滤波器相当于是在传统L型滤波器两个滤波电感之间增加了一个滤波电容，利用电容的高频低阻抗特性对谐波进行旁路，从而实现了比L型滤波器更好的滤波效果。而LLCL型滤波器可以认为是LCL型滤波器的改进型，即在电容支路上再串联一个小电感，通过LfCf支路对PWM开关频率次谐波的陷波作用实现更好的高频谐波衰减效果。

图1 L、LCL和LLCL型滤波器结构Fig.1 Structures of L,LCL and LLCL filters

由图1可推导出L型、LCL型和LLCL型滤波器的导纳传递函数，即并网电流ig相对于逆变器输出电压uinv的信号增益，分别如式（1）、式（2）和式（3）所示。

由式（3）可推导出 LLCL型滤波器的LfCf支路串联谐振频率为

根据式（1）、式（2）和式（3）可以绘制出三种滤波器导纳传递函数的幅频特性曲线，如图2所示。图中，横坐标为频率f，纵坐标为幅值M，fres_LCL为LCL型滤波器的固有谐振频率，fres_LLCL为 LLCL型滤波器的固有谐振频率。为便于比较，三种滤波器的Linv和Lg取值相同，LCL型和LLCL型滤波器的Cf取值也相同。

图2 L型、LCL型和LLCL型滤波器的导纳幅频特性Fig.2 Amplitude-frequency admittance characteristics of L,LCL and LLCL filters

从图2可以看出，由于Lf电感值远远小于Linv和Lg，则fres_LCL和fres_LLCL非常接近，即三种滤波器在低频段（低于固有谐振频率）几乎拥有相同的幅频特性，因此不会影响控制系统的环路带宽，保证了并网系统的动态性能和低频谐波抑制能力。而在高频段（高于固有谐振频率），L型滤波器以每10倍频程-20dB的速率衰减，LCL型滤波器以每10倍频程-60dB的速率衰减，LLCL型滤波器以每10倍频程-40dB的速率衰减。虽然在整个高频段LLCL型滤波器比LCL型滤波器的衰减性能要差，但是若调整LfCf支路参数使 PWM 开关频率fsw=fs_LLCL，则LLCL型滤波器能够对逆变器侧高频谐波中最主要的开关频率次谐波得到极大衰减。由此可见，LLCL型滤波器是以适当牺牲整个高频段的衰减速率来换取对某个特定频率谐波的极大衰减，只要参数设计合理，LLCL型滤波器的整体滤波效果会明显优于LCL型滤波器，从而在保证滤波效果相同的情况下大大减小Lg的电感值。

对于 LCL型滤波器，当固有谐振频率fres_LCL取值太小容易引起逆变器侧非线性导致的低次谐波被放大而引起并网电流畸变，而取值太大又会降低滤波器对高频谐波的衰减能力。为保证有效抑制开关频率次谐波同时系统仍具有良好的动态性能，一般取 10fg＜fres_LCL＜0.5fsw，fg为电网基波频率。然而，对于LLCL型滤波器，由于占谐波主要成分的开关频率次谐波被LfCf陷波器旁路，因此滤波器的固有谐振频率fres_LLCL可以取得较高，这不但有利于固有谐振尖峰的阻尼和稳定控制系统的设计，而且能够提高系统带宽，这也是LLCL型相比LCL型滤波器的一个突出优点。

3 基于滤波器统一模型的新型拓扑推演

随着近几年新能源发电所占能源结构比重的不断提高，并网逆变器逐渐向高效率低成本和大功率低损耗方向发展。对于小功率应用场合，希望在同样开关频率的情况下进一步减小并网滤波器电感值（滤波器的体积和成本主要由滤波电感决定）。对于大功率应用场合，由于受到开关损耗限制，功率器件的开关频率选择都比较低，因此希望滤波器在较低开关频率下同样能够实现良好的滤波效果。

通过对现有三种滤波器拓扑结构及特性的分析可知，LCL型和LLCL型滤波器都是在L型拓扑结构的基础上改进而来的，即在逆变器侧滤波电感Linv和网侧电感Lg中间增加一个对高频谐波电压呈低阻抗的支路，使并网电流中的高频谐波成分得到比L型滤波器更好的抑制效果。基于现有滤波器的拓扑结构及滤波特性，本文提出一种并网接口滤波器统一电路模型，如图3所示。与LCL型和LLCL型滤波器的滤波原理一致，通过图中Zh支路的高频旁路作用抑制逆变器侧高频谐波电流注入电网，实现比上述三种滤波器更好的滤波效果，从而进一步减小滤波器成本和体积。

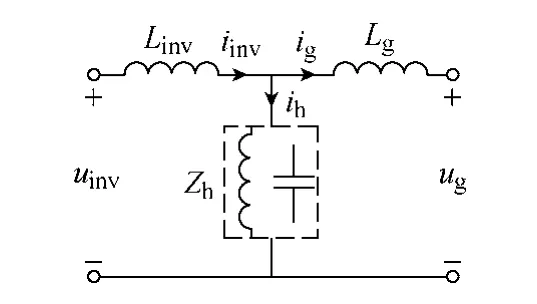
图3 并网接口滤波器统一电路模型Fig.3 Unified circuit model of grid-interfacing filters

忽略电容电感的寄生参数，构成滤波器的基本元件是电容和电感。本文对Zh支路在三阶以下（即不超过3个基本元件）所有可能的拓扑结构进行推演与分析，即构成Zh支路可以是1个、2个或3个基本元件。通过不同个数基本元件的不同串并联组合，可以得到不同拓扑结构的滤波器。采用1个基本元件时，Zh支路为纯电感或者纯电容支路，当该支路为纯电容时即为图1b所示的LCL型滤波器，当该支路为纯电感时如图4a所示。采用2个基本元件时，Zh支路为电感电容串联或并联，当串联时即为LLCL型滤波器（见图1），并联时如图4b所示。同理，采用3个基本元件时，通过电感和电容的不同拓扑组合，可以得到图4c～图4f所示的四种滤波器拓扑结构。

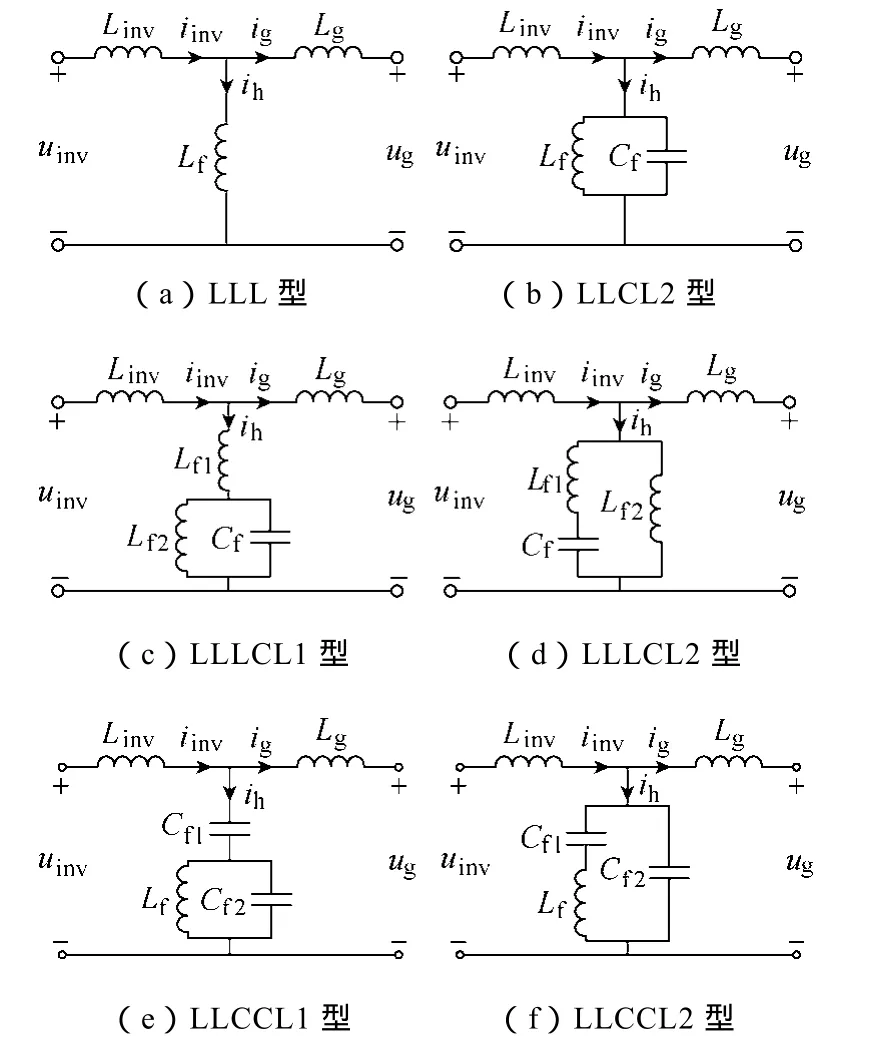
图4 基于不同Zh支路结构的滤波器拓扑Fig.4 Topologies of grid-interfacing filters with different structures of shunt branchZh

通过上述对L型、LCL型和LLCL型滤波器的滤波特性分析发现，一个并网接口滤波器的幅频特性曲线可以以固有谐振频率作为分界点，分为低频段和高频段。在低频段，主要是频率为电网频率fg的基波成分和由于逆变器非线性特性和电网电压畸变而引入的低频谐波成分。对于低频谐波给并网电流质量带来的影响，仅仅依靠滤波器本身结构无法得到有效抑制，主要是通过改进并网控制策略加以抑制。在高频段，主要是PWM开关频率fsw、2倍及多倍开关频率次频谐波成分。因此，从滤波器频率特性角度看，分析滤波器低频特性时主要关心的频率是fg，而分析高频特性时主要关心的频率是fsw和2fsw。

并网接口滤波器是逆变器与电网的接口，其主要功能是将逆变桥输出 PWM电压中占主导地位的基波电压通过滤波器转化为电网基波电流输送给公共电网，同时对 PWM电压中的高频谐波进行有效抑制。因此，Zh支路在低频段应呈高阻抗，以保证能将逆变器输出电压中的基波成分传递到电网，而在高频段应呈低阻抗，以保证良好的高频谐波旁路作用。换句话说，希望Zh支路低频时是电容，高频时仍是电容，即具有 LCL型滤波器的拓扑结构特点。而且，如果希望对特定频率的谐波成分实现陷波效果，如占主导地位的开关频率次谐波成分，则可以通过调整Zh支路参数使该支路在该特定频率处发生串联谐振而呈现接近零阻抗特性，即具有LLCL型滤波器的拓扑结构特点。

从图4中的六种新型滤波器拓扑结构发现，其中图 4a～4d四种拓扑结构中均包含有Zh支路两端之间的直接电感连接，由于电感在基频时阻抗非常小，因此会造成基波成分的严重分流，从而大大降低并网逆变系统的功率传输效率，而且对于图4a～图4d三种拓扑结构，由于电感在高频时阻抗非常大，也不利于高频谐波衰减。因此，上述四种滤波器均不适合作为并网接口滤波器使用。图4e和图4f两种拓扑结构均包含有Zh支路两端之间的直接电容连接，因为电容的低频高阻抗特性能够保证基波成分传递到电网及其高频低阻抗特性能够对高频谐波成分有效衰减，因此这两种拓扑结构显然能够用来作为并网接口滤波器使用，本文定义图 4e的拓扑为LLCCL1型滤波器，定义图4f的拓扑为LLCCL2型滤波器。

4 新型/现有滤波器特性分析与比较

4.1 导纳特性分析与比较

由LLCCL1型和LLCCL2型滤波器的拓扑结构可推导出并网电流ig相对于逆变器输出电压uinv的导纳传递函数，分别如式（5）和式（6）所示。由式（5）和式（6）可推导出两种新型滤波器的Zh支路串联谐振频率，分别为

为保证L型、LCL型、LLCL型、LLCCL1型和LLCCL2型滤波器在相同体积和成本情况下进行分析与比较，取Cf1+Cf2=Cf，另外考虑到实际逆变器系统中对电容器配置与安装的方便性，可以取Cf1=Cf2。由式（4）、式（7）和式（8）可知，为实现LLCL型、LLCCL1型和LLCCL2型滤波器对开关频率次谐波的陷波效果，可调整Zh支路参数使Zh支路串联谐振频率完全相同。虽然电容对滤波器体积和成本影响不大，但太大的滤波电容会导致系统功率因数过低而影响并网性能，而Zh支路的滤波电感相比Linv和Lg在体积和成本上可以忽略，因此本文通过调整Lf的电感值实现滤波器对开关频率次谐波的陷波作用。五种滤波器导纳传递函数的幅频特性曲线如图5所示。图中，fres_LLCCL1和fres_LLCCL2分别为LLCCL1型和LLCCL2型滤波器的固有谐振频率，fp_LLCCL1和fp_LLCCL2分别为 LLCCL1型和LLCCL2型滤波器的高频谐振频率。

从图 5a可以发现，LLCCL2型滤波器与 LCL型及 LLCL型滤波器的低频特性基本一致，而LLCCL1型滤波器的低频特性要优于其他几种滤波器。在高频段，LLCCL1型和LLCCL2型滤波器不但同LLCL型滤波器一样能够对开关频率次谐波起到陷波作用，而且在整个高频段还具有LCL型滤波器每 10倍频程接近-60dB速率衰减高频谐波的优点。因此，在相同参数下两种新型拓扑结构的滤波器会实现比现有滤波器更好的高频谐波衰减效果。通过图 5b所示导纳幅频特性曲线的局部放大图可以进一步看出，LCL型滤波器的高频衰减速率要略优于LLCCL1型和LLCCL2型，这主要是因为LCL型的Zh支路是纯电容，而两种新型滤波器的Zh支路都包含了滤波电感。另外，从图5还可以看到，两种新型滤波器除了存在一个固有谐振尖峰外，在高频段还存在一个高频谐振尖峰，因此在进行有源或无源阻尼时需要比现有滤波器考虑更多的因素，但这并不影响两种新型滤波器对并网电流谐波具有更好衰减特性的优点。

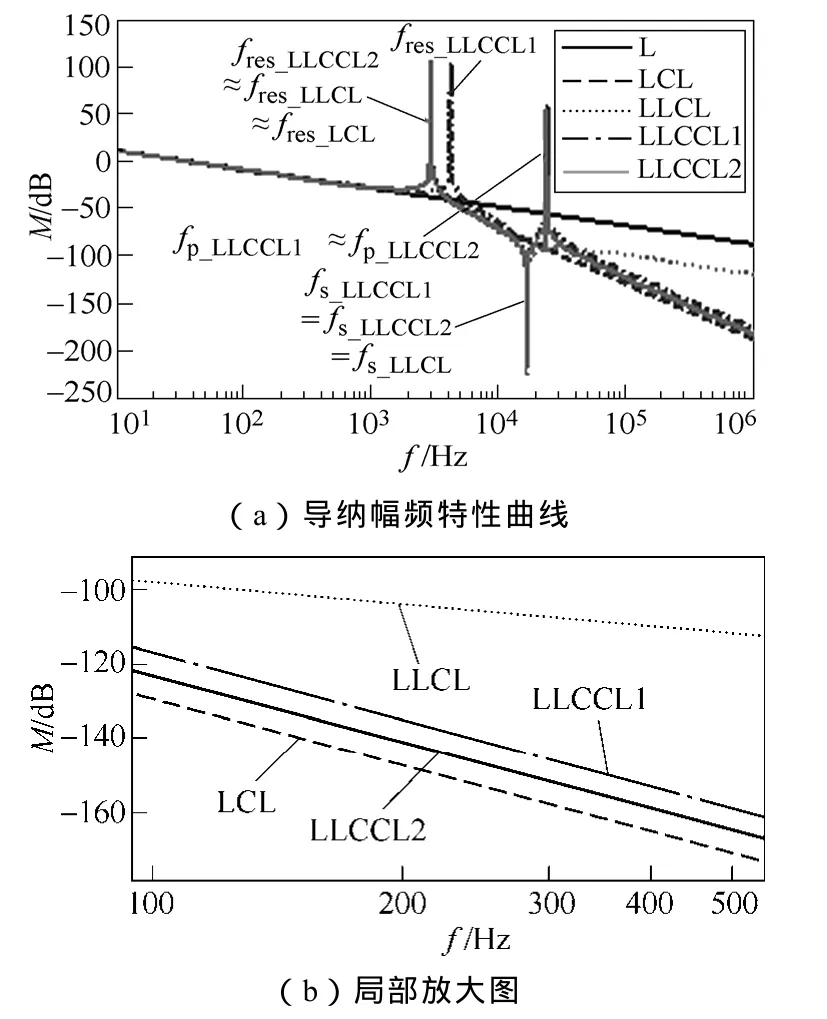
图5 五种滤波器的导纳幅频特性Fig.5 Amplitude-frequency admittance characteristics of the five filters

4.2 阻抗特性分析与比较

在实际电网中，大量基于电力电子变流技术的变频电源和开关电源等设备都不同程度地对电网造成谐波污染，导致电网电压中除了含有基波和低频谐波外，有时还包含有高频成分。并网接口滤波器在抑制逆变器高频谐波进入电网的同时，若滤波器本身能对网侧高频谐波也具有一定的抑制能力，阻止电网高频谐波进入逆变器，则有利于并网逆变器的可靠运行和高性能并网，而且在一定程度上也能够降低电磁干扰滤波器的成本，从而降低并网逆变器整机成本。若将一个并网接口滤波器看成两端口电路网络，则既不希望逆变器PWM调制产生的高频成分通过滤波器向电网注入，也不希望电网中高频谐波反过来干扰并网逆变器正常运行，同时还必须保证将 PWM输出波形中基波成分以尽量少的损耗从分布式发电装置输送到电网。因此，希望接口滤波器能够对低频（主要指基波分量，对于低频谐波的影响主要通过并网电流控制手段加以抑制）分量呈低阻抗，对高频谐波分量呈高阻抗。也就是说，希望并网逆变器低频时是电感，高频时仍是电感。

由拓扑结构图可推导出 L型、LCL型、LLCL型、LLCCL1型和LLCCL2型滤波器的阻抗传递函数，即电网电压ug相对于并网电流ig的信号增益，如表1所示。显然，一个并网接口滤波器在高频段的阻抗传递函数幅值越高，则滤波器对电网高频谐波的抑制能力越强，因而并网逆变器的抗干扰能力也越强。五种滤波器阻抗传递函数的幅频特性曲线如图6所示。

表1 五种滤波器的阻抗传递函数Tab.1 Impedance transfer functions of the five filters

图6 五种滤波器的阻抗幅频特性Fig.6 Amplitude-frequency impedance characteristics of the five filters

从图 6a可以看出，相同参数下传统 L型滤波器对电网高频谐波的抗干扰能力反而越强，这是因为其他四种滤波器的Zh支路在对逆变器侧高频谐波进行有效旁路以满足并网电流质量要求的同时，也降低了滤波器对电网高频谐波的抑制能力。通过图 6b所示阻抗幅频特性曲线的局部放大图可以进一步看出，LCL型、LLCCL1型和LLCCL2型滤波器对电网高频谐波的抗干扰能力都远不如L型滤波器。LLCL型滤波器因其Zh支路中串联的电感Lf在高频时呈现高阻特性，使其抗干扰效果仅次于L型滤波器。当然，由于Lf电感值远小于逆变器侧电感Linv，而加大Lf电感值又与降低滤波器成本和体积相矛盾，因此其抗干扰能力也有限，但这不失为LLCL型滤波器的一个优点。

4.3 滤波器参数设计

关于LCL型和LLCL型滤波器的参数设计要求和约束条件，文献[12～15]已经进行过详细的研究，归纳起来主要有以下几点：

（1）在直流侧母线电压和电网电压一定的情况下，滤波器总电感Linv+Lg数值越大，并网电流纹波越小，滤波效果也就越好。但电感值的增加会减小电感电流变化率，影响系统动态性能。由于基频时电容相当于开路，因此结合传统L型滤波器设计经验，通常使Linv+Lg所产生的阻抗压降小于额定电网电压的10%。

（2）逆变器侧电感电流iinv的纹波限值决定着滤波电感Linv的大小。通常取流过Linv的电流纹波小于额定电流峰值的25%。

（3）网侧电感电流ig的纹波限值决定着滤波电感Lg的大小。以标准IEEE Std 1547—2003为例，除规定分布式电源系统并网电流的总谐波畸变率（Total Harmonic Distortion，THD）必须小于5%之外，还要求3～9次谐波小于4%，11～15次谐波小于2%，17～21次谐波小于1.5%，23～33次谐波小于0.6%，33次以上谐波小于0.3%，偶次谐波应小于相对较低奇次谐波限值的25%。逆变器PWM开关频率通常在10kHz以上，产生的谐波都远远高于33次，而滤波器的高频谐波衰减特性随着频率的增大而增强，因此只要保证开关频率及其边带次谐波含量小于0.3%，则其他高频谐波均能满足并网电流谐波要求。以单相全桥并网逆变器为例，根据式2Udc|Jmax(mπ)|·|G(j2πfh)|/(πIref)＜0.3%可以设计Lg的参数范围，其中Udc为直流母线电压，Jmax为第一类贝塞尔函数，|G(j2πfh)|为滤波器导纳传递函数在频率fh处的幅值绝对值，Iref为并网电流给定值，m为调制比。对于LCL型滤波器，可以按照fh=fsw设计Lg参数。对于LLCL型滤波器，可以按照fh=2fsw设计Lg参数，通常Lg是LCL型滤波器情况时的1/6左右[10]。

（4）总电感Linv+Lg数值和滤波电容Cf一定的情况下，Linv/Lg=1时滤波器的高频衰减效果达到最好，但此时固有谐振频率也最低，因此不利于控制系统的设计。对于 LCL型滤波器，通常可以取Linv/Lg=1～3，对于 LLCL型滤波器，通常可以取Linv/Lg=5～7。

（5）滤波电容Cf数值越大，对高频开关谐波的衰减能力越强，滤波效果也越好。虽然电容对滤波器体积重量和成本影响不大，增大电容一定程度上可以减小滤波电感值，但同时也会吸收更多的无功功率，导致逆变器功率因数过低而整机效率下降。通常要求滤波电容Cf吸收的无功功率小于系统额定功率的5%。

（6）滤波器的滤波原理可以理解为滤波电容Zh支路和网侧电感Lg支路构成并联电路对高频谐波进行分流。因此，对于LCL型和LLCL型滤波器都存在Cf越大或者Lg越大，滤波效果也越好，但电容太大会导致并网逆变器功率因数下降，而电感太大会导致Linv+Lg阻抗压降太大和滤波器体积成本增加。通常要求滤波电容容抗Zf为网侧电感感抗Zg的0.1～0.2倍。

（7）固有谐振频率越大，滤波器低频特性越好，越有利于并网电流控制器设计，但太大的谐振频率会导致滤波器高频衰减性能变差，影响整体滤波效果。因此，为兼顾高频特性和低频特性，通常使固有谐振频率大于电网频率fg的 10倍，而小于开关频率fsw的0.5倍。

（8）对于LLCL型滤波器，还必须保证开关频率fsw等于LfCf支路串联谐振频率，即满足式（4）。

对于 LLCCL1型和LLCCL2型两种新型滤波器，约束条件（8）需要分别修改为Zh支路满足式（7）和式（8）。另外，对于约束条件（3），还需要保证高频谐振频率fp_LLCCL1和fp_LLCCL2附近的并网电流谐波成分幅值仍然小于0.3%。其余6条约束条件与LCL型和LLCL型滤波器完全相同。此外，考虑到一个并网接口滤波器的体积和成本都主要由滤波电感决定，因此在满足上述约束条件的基础上可以尽量使电感参数取值小一些。取系统参数如下：电网电压有效值Ug=220V/50Hz，并网电流有效值Ig=7.07A，直流母线电压Udc=400V，开关频率fsw=16kHz。根据上述滤波器参数设计要求和系统参数，本文设计出L型、LCL型、LLCL型、LLCCL1型和LLCCL2型滤波器的一组参数见表2。

表2 五种滤波器的参数Tab.2 Parameters of the five filters

4.4 谐振阻尼分析

除L型滤波器外，其余四种都属于高阶滤波器，导纳传递函数在虚轴上存在的共轭极点会导致其幅频特性曲线存在谐振尖峰，降低滤波器在该频率点处的阻抗特性，影响并网电流质量或引起系统不稳定。为保证并网系统安全稳定运行，需要通过有源阻尼或无源阻尼策略来抑制滤波器的谐振现象。有源阻尼是通过控制算法来实现谐振尖峰抑制，因此不会增加系统损耗，但复杂的控制算法和额外增加的电压或电流传感器会使整个并网逆变器成本增加，系统可靠性和鲁棒性也降低。无源阻尼因其实现简单、成本低廉等优点而在工业中被广泛应用[17,18]。无源阻尼又分为电容支路串联电阻和电容支路并联电阻两种，考虑到无源阻尼最大缺点是增加系统功率损耗，而当出现滤波电容两端或者Zh支路两端直接电阻并联的情况时会带来较大的低频（基波）功率损耗，因此本文采用的无源阻尼方案都是在保证Zh支路不出现上述低频低阻抗通路的基础上进行谐振尖峰阻尼分析。

对于 LCL型滤波器，Cf串联电阻可以阻尼固有谐振尖峰，电阻越大阻尼效果越好，但高频谐波衰减特性也会下降。对于LLCL型滤波器，同样是Cf串联电阻来阻尼固有谐振尖峰，电阻越大阻尼效果越好，但同时也导致LfCf支路对开关频率次谐波的陷波效果下降，这是该滤波器的不足之处。太大的阻尼电阻会导致丢失滤波器对开关频率次谐波的陷波作用这个优点，而太小的阻尼电阻又会降低系统控制带宽，不利于系统稳定运行。对于LLCCL1型滤波器，当Cf1串联电阻时只能阻尼固有谐振尖峰，当Cf2串联电阻只能阻尼高频谐振尖峰，只有当Cf1和Cf2都串电阻时才可同时阻尼两个谐振尖峰。由于这3种阻尼方案在抑制谐振尖峰的同时，也都会抑制Zh支路对开关频率次谐波的陷波效果，因此对于LLCCL1型滤波器，最恰当的阻尼方案显然是Cf1和Cf2均串联电阻，而且阻尼电阻的大小取值需要在系统稳定性和开关频率次谐波陷波作用之间折中处理。对于 LLCCL2型滤波器，当Cf1串联电阻时既可以阻尼固有谐振尖峰也可以阻尼高频谐振尖峰，当Cf2串联电阻时同样可以实现同时阻尼两个谐振尖峰的作用。而从LLCCL2型滤波器的拓扑结构可以看出，Cf2串联电阻时在阻尼谐振尖峰的同时不会影响LfCf支路对开关频率次谐波的陷波作用。当然，Cf2串联电阻时滤波器开关频率次谐波之外的高频衰减特性要比Cf1串联电阻时差些，此处采用Cf2串联阻尼电阻，以保证滤波器对开关频率次谐波具有良好的陷波作用。

加入无源阻尼后四种滤波器的拓扑结构如图 7所示，根据表2参数可绘制出对应的导纳传递函数幅频特性曲线，如图8a所示。当所有滤波器的阻尼电阻都取Rd=8Ω时，对应的幅频特性曲线如图 8b所示。从图8可以看出，随着阻尼程度的加深，谐振尖峰被越来越好地抑制，也越来越有利于并网系统的稳定运行。然而LLCL型和LLCCL1型滤波器对开关频率次谐波陷波这个优点逐渐失去，按照表2参数取值已经达不到LCL型滤波器的滤波效果，而要提高滤波效果只能增大网侧电感值。对于LLCCL2型滤波器，其陷波作用没有得到任何影响，并且与无阻尼情况相比，其固有谐振尖峰也被抑制到足够满足控制环路带宽要求，因此相对来说滤波效果最好。

图7 四种滤波器的无源阻尼结构Fig.7 Structures of the four filters with passive damping resistors

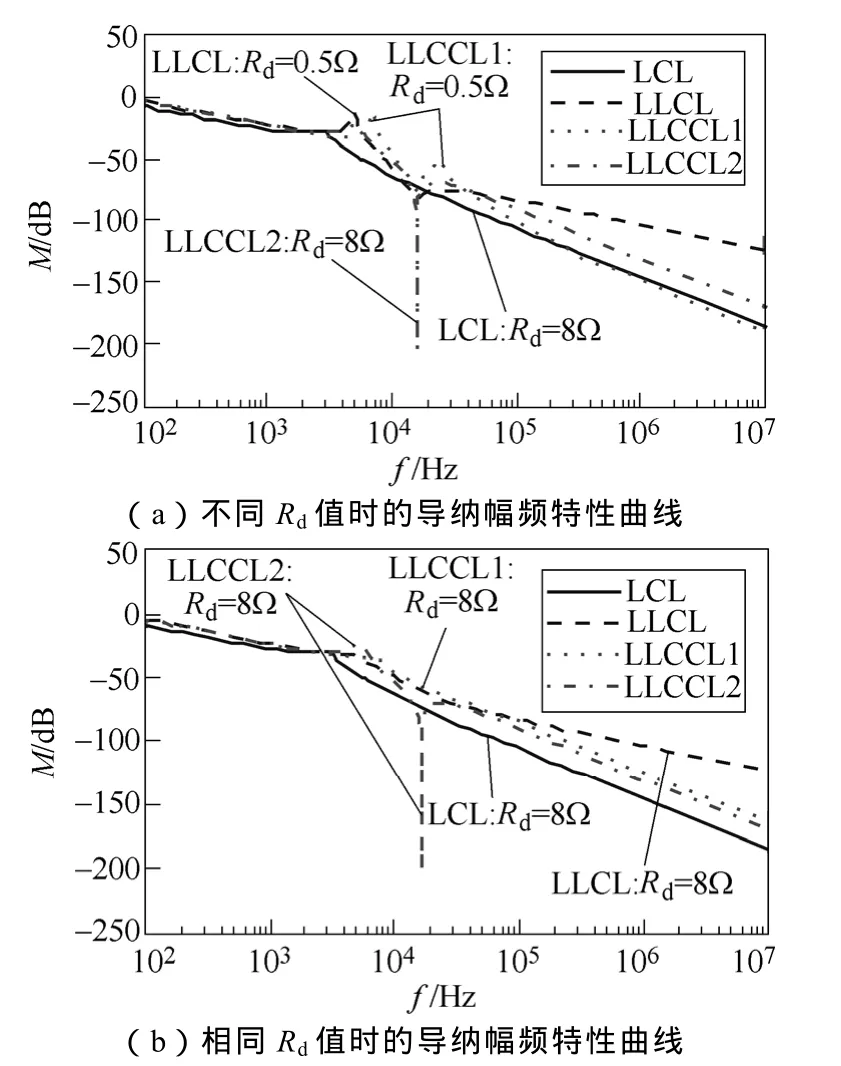
图8 无源电阻阻尼时四种滤波器的导纳幅频特性Fig.8 Amplitude-frequency admittance characteristics of the four filters with passive damping resistors

综上所述，从并网接口滤波器对逆变器侧高频谐波的衰减特性以及对开关频率次谐波的陷波效果角度看，LLCCL2型滤波器要略好于LLCCL1型，其余依次是LLCL型、LCL型和L型。从滤波器对电网侧高频谐波的抗干扰能力角度看，L型滤波器要远好于其他四种滤波器，其余依次是LLCL型、LCL型、LLCCL2型和LLCCL1型，当然LLCL型的抑制能力相对而言要明显优于另外三种滤波器。从是否有利于并网电流控制器设计角度看，由于LLCL型、LLCCL1型和LLCCL2型要比LCL型滤波器能够设置更高的固有谐振频率，特别是LLCCL1型滤波器在相同参数下低频特性要相对更好。然而，为保证并网逆变器稳定可靠运行，在实际中必须对滤波器的固有谐振尖峰和高频谐振尖峰进行有效阻尼。而对于LLCL型和LLCCL1型滤波器，随着阻尼效果的增强，滤波器对开关频率次谐波的陷波作用这个优点会逐渐变弱。此外，LLCCL2型滤波器对开关频率次谐波的陷波作用并没有因阻尼而减弱，因此其整体滤波效果通常会明显优于其他滤波器，这是该滤波器的一个突出优点。从滤波性能、装置体积成本及系统稳定性等角度综合比较五种滤波器，本文推荐使用LLCCL2型。当然，在实际并网逆变系统中，结合滤波器的逆变器侧谐波衰减特性和网侧谐波抑制特性，可根据具体情况折中选择最适合实际情况的滤波器拓扑结构类型。

5 仿真研究

为验证LLCCL1型和LLCCL2型滤波器的正确性和可行性，以及与现有滤波器的特性对比，在PSIM 环境下搭建了单相全桥并网逆变器，系统结构如图9所示。图中，VT1～VT4为开关管，VD1～VD4为反并联二极管，Cdc为直流母线电容。采用双极性 SPWM调制技术，因此逆变桥输出高频谐波中最主要成分为开关频率次谐波，开关频率为16kHz。

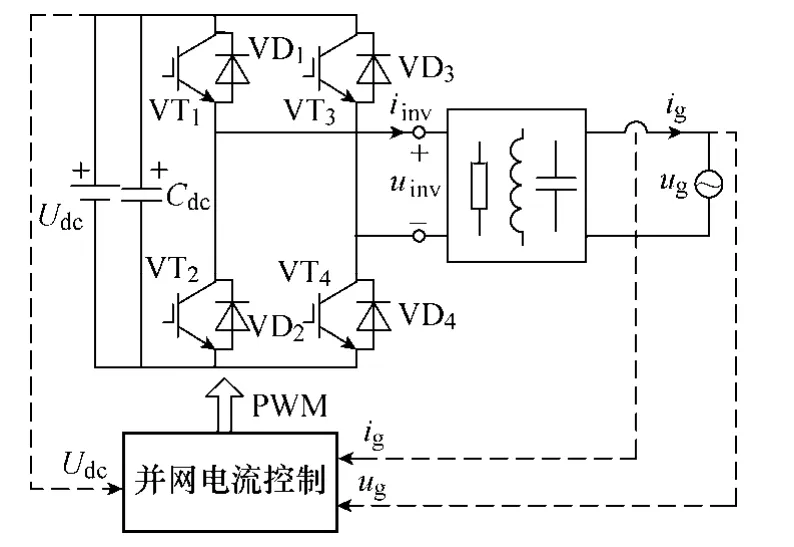
图9 单相并网逆变器系统结构Fig.9 Single-phase grid-connected inverter system

由于滤波器的固有谐振尖峰和高频谐振尖峰采用无源阻尼抑制，因此控制系统采用直接并网电流单环反馈控制。为更好地比较不同滤波器的滤波效果，系统参数和滤波器参数与 4.3节相同，阻尼电阻与图 8a相同，并网控制均采用经典的比例积分调节器，而且所取参数也完全相同，比例系数KP=0.05，积分系数KI=5 000s-1。四种滤波器的系统开环传递函数波特图如图10所示。采用LCL型、LLCL型、LLCCL1型和LLCCL2型滤波器时的并网电流分别表示为ig_LCL、ig_LLCL、ig_LLCCL1和ig_LLCCL2，仿真波形如图11所示，对应并网电流的THD见表3。

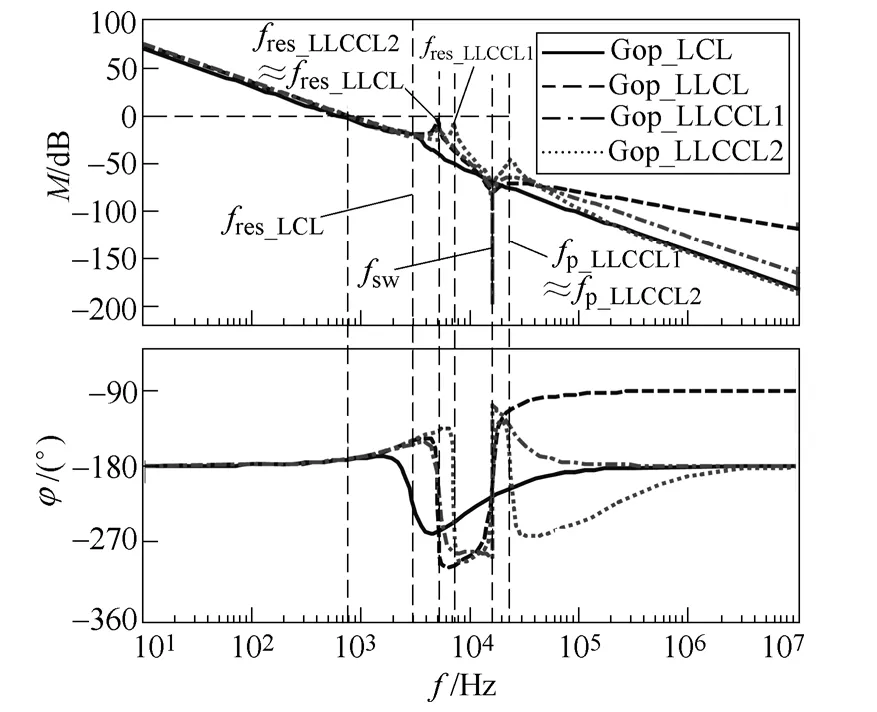
图10 四种滤波器的系统开环传递函数伯德图Fig.10 Bode diagrams of open-loop transfer functions of inverter system with the four filters

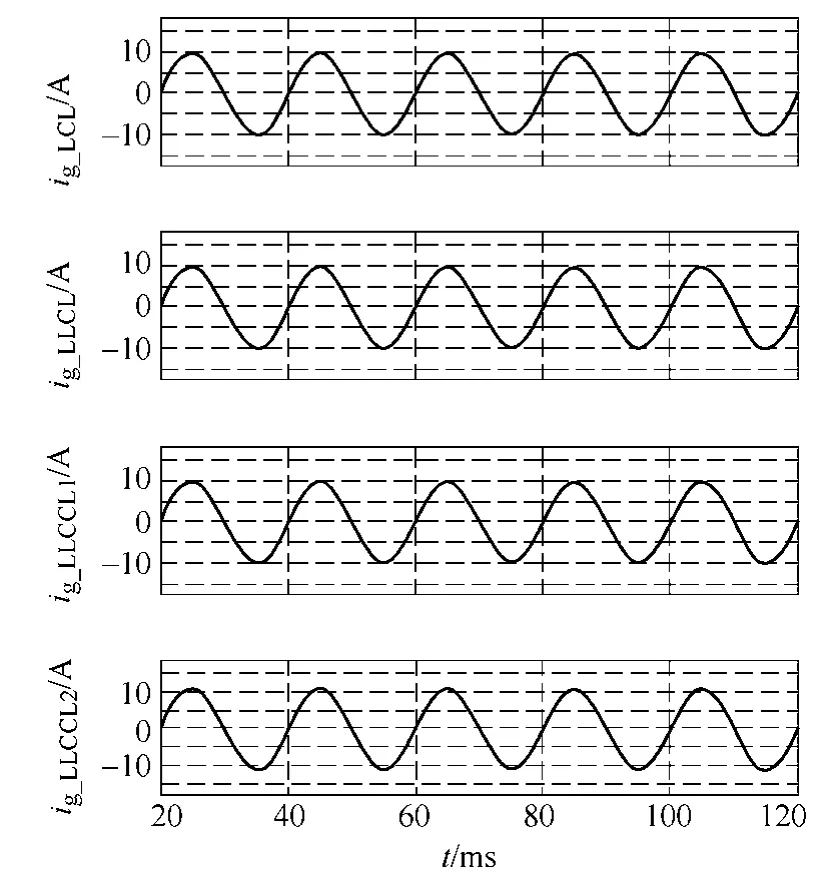
图11 四种滤波器的并网电流比较Fig.11 Grid current comparisons of the four filters

表3 4种滤波器的并网电流谐波畸变率Tab.3 THD of grid currents of the four filters

从表中可以看出，LLCL型、LLCCL1型和LLCCL2型滤波器在网侧滤波电感Lg比LCL型小6倍左右的情况下仍然能够获得非常好的并网滤波效果。

并网电流在特定频率处的谐波频谱如图12所示。从图12a可以看出，LLCCL2型滤波器对开关频率（16kHz）次谐波的抑制效果要明显好于其他三种滤波器，与 4.4小节理论分析完全一致，且从表3中也可以看出采用该滤波器时并网电流的THD最小。注意到由于阻尼电阻降低了滤波器的高频衰减能力，导致LCL型和LLCCL1型滤波器在开关频率处的谐波电流幅值超过了 0.3%（30mA），因此需要减小阻尼电阻并降低控制带宽来满足单次谐波要求。从图12b可以看出，虽然LLCL型和LLCCL1型在固有谐振频率（分别为 4.8kHz和5.9kHz）附近的谐波电流幅值小于0.3%，但相比另外两种滤波器要偏高。从图12c可以看出，由于LLCCL1型的高频谐振尖峰阻尼程度较弱，在高频谐振频率（24kHz）附近的谐波被放大。当然，该频率已远高于开关频率，在设计中只要加以适当阻尼并且避开两倍开关频率点，就容易满足单次谐波要求。

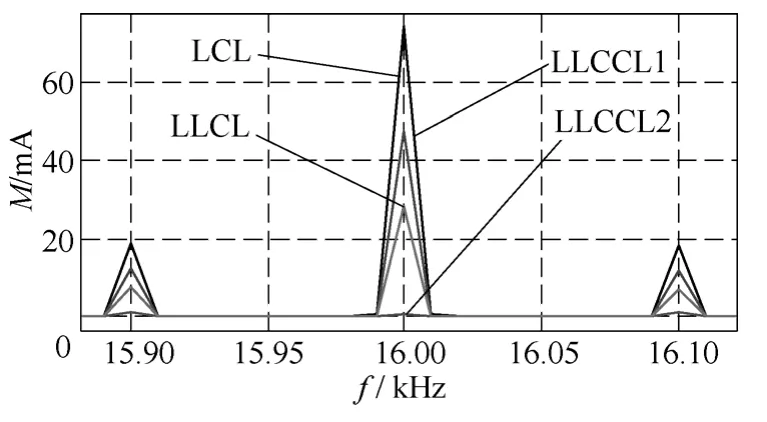
（a）开关频率附近的电流谐波幅值

图12 四种滤波器在特定频率处的电流谐波幅值比较Fig.12 Magnitude comparisons of grid harmonic currents of the four filters at the special frequency

综上分析，所推演出的LLCCL2型滤波器作为不同于现有三种滤波器的第四种新型并网接口滤波器，具有较好的滤波效果，值得关注和进一步的实验研究。

6 结论

在深入分析L型、LCL型及LLCL型并网接口滤波器高频谐波衰减性能和拓扑结构特点的基础上，提出了一种并网接口滤波器统一电路模型，并推演出两种新型滤波器，LLCCL1型和LLCCL2型。通过对新型和现有滤波器在滤波特性、阻抗特性、参数设计及谐振尖峰阻尼等方面的详细对比研究发现，LLCL型及两种新型滤波器由于能够实现对PWM 调制中最主要的开关频率次谐波起到陷波作用，因此在满足相同并网要求的情况下能够在LCL型的基础上进一步减少滤波器的体积和成本，并且在相同参数下LLCCL2型滤波器的高频衰减性能要明显好于其他滤波器。此外，LCL型、LLCL型和LLCCL1型滤波器在采用无源阻尼抑制固有谐振尖峰或高频谐振尖峰的同时，也会降低滤波器高频谐波的衰减能力和开关频率次谐波的陷波作用，而LLCCL2型滤波器对开关频率次谐波的陷波作用几乎可以不受谐振尖峰阻尼效果的影响，因此在实际工程中会实现更好的并网谐波抑制效果。

[1] Wang F,Duarte J L,Hendrix M A M,et al. Modeling and analysis of grid harmonic distortion impact of aggregated DG inverters[J]. IEEE Transactions on Power Electronics,2011,26(3): 786-797.

[2] Castilla M,Miret J,Matas J,et al. Control design guidelines for single-phase grid-connected photovoltaic inverters with damped resonant harmonic compensators[J]. IEEE Transactions on Industrial Electronics,2009,56(11): 4492-4501.

[3] Liserre M,Teodorescu R,Blaabjerg F. Stability of photovoltaic and wind turbine grid-connected inverters for a large set of grid impedance values[J]. IEEE Transactions on Power Electronics,2006,21(1): 263-272.

[4] 王学华,阮新波,刘尚伟. 抑制电网背景谐波影响的并网逆变器控制策略[J]. 中国电机工程学报,2011,31(6): 7-14.

Wang Xuehua,Ruan Xinbo,Liu Shangwei. Control strategy for grid-connected inverter to suppress current distortion effected by background harmonics in grid voltage[J]. Proceedings of the CSEE,2011,31(6): 7-14.

[5] Gabe I J,Montagner V F,Pinheiro H. Design and implementation of a robust current controller for VSI connected to the grid through an LCL filter[J]. IEEE Transactions on Power Electronics,2009,24(6): 1444-1452.

[6] Khajehoddin S A,Ghartemani M K,Jain P K,et al. A control design approach for three-phase grid-connected renewable energy resources[J]. IEEE Transactions on Sustainable Energy,2011,2(4): 423-432.

[7] Lindgren M,Svensson J. Connecting fast switching voltage-source converters to the grid-harmonic distortion and its reduction[C]. Strock Power Tech. Conference,Stockholm: IEEE,1995: 191-195.

[8] 王斯然,吕征宇. LCL型并网逆变器中重复控制方法研究[J]. 中国电机工程学报,2010,30(27): 69-75.

Wang Siran,Lü Zhengyu. Research on repetitive control method applied to grid-connected inverter with LCL filter[J]. Proceedings of the CSEE,2010,30(27): 69-75.

[9] 胡雪峰,龚春英,陈新,等. 三相 T型滤波并网逆变电源的网侧电流直接控制技术[J]. 电工技术学报,2012,27(1): 9-16.

Hu Xuefeng,Gong Chunying,Chen Xin,et al. Direct grid current control of the three-phase grid-connected inverter through T filter[J]. Transactions of China Electrotechnical Society,2012,27(1): 9-16.

[10] Wu W,Blaabjerg F. An LLCL power filter for singlephase grid-tied inverter[J]. IEEE Transactions on Power Electronics,2012,27(2): 782-789.

[11] Liserre M,Blaabjerg F,Hansen S. Design and control of an LCL filter-based three-phase active rectifier[J].IEEE Transactions on Industrial Applications,2005,41(5): 1281-1291.

[12] 刘飞,查晓明,段善旭. 三相并网逆变器 LCL滤波器的参数设计与研究[J]. 电工技术学报,2010,25(3): 110-116.

Liu Fei,Zha Xiaoming,Duan Shanxu. Design and research on parameter of LCL filter in three-phase grid-connected inverter[J]. Transactions of China Electrotechnical Society,2010,25(3): 110-116.

[13] Jalili K,Bernet S. Design of filters of active-front-end two-level voltage-source converters[J]. IEEE Transactions on Industrial Electronics,2009,56(5): 1674-1689.

[14] Wu Weimin,Huang Min,Sun Yunjie,et al. A composite passive damping method of the LLCL-filter based gridtied inverter[C]. IEEE International Symposium on Power Electronics for Distributed Generation Systems,Aalborg,2012: 759-766.

[15] Pena-Alzola R,Liserre M,Blaabjerg F,et al. Analysis of the passive damping losses in LCL-filter-based grid converters[J]. IEEE Transactions on Power Electronics,2013,28(6): 2642-2646.

[16] 张宪平,李亚西,许洪华. 新型拓扑滤波器的双馈风电网侧变流器阻尼策略[J]. 中国电机工程学报,2009,29(21): 1-7.

Zhang Xianping,Li Yaxi,Xu Honghua. Damping strategy of grid-side converter with new topology filter in doubly-fed wind power system[J]. Proceedings of the CSEE,2009,29(21): 1-7.

[17] 伍小杰,孙蔚,戴鹏,等. 一种虚拟电阻并联电容有源阻尼法[J]. 电工技术学报,2010,25(10): 122-128.

Wu Xiaojie,Sun Wei,Dai Peng,et al. An active damping method of virtual resistor[J]. Transactions of China Electrotechnical Society,2010,25(10): 122-128.

[18] 王要强,吴凤江,孙力,等. 阻尼损耗最小化的LCL滤波器参数优化设计[J]. 中国电机工程学报,2010,30(27): 90-95.

Wang Yaoqiang,Wu Fengjiang,Sun Li,et al. Optimized design of LCL filter for minimal damping power loss[J]. Proceedings of the CSEE,2010,30(27): 90-95.

[19] 许津铭,谢少军,肖华锋. LCL滤波器有源阻尼控制机制研究[J]. 中国电机工程学报,2012,32(9):27-33.

Xu Jinming,Xie Shaojun,Xiao Huafeng. Research on control mechanism of active damping for LCL filters[J]. Proceedings of the CSEE,2012,32(9): 27-33.