基于Crowbar的双馈机组风电场等值模型与并网仿真分析

王振树 刘 岩 雷 鸣 卞绍润 石云鹏

（1. 山东大学电气工程学院 济南 250061 2. 国网青岛供电公司 青岛 266100 3. 国家电网山东电力公司调度控制中心 济南 250001 4. 国网历城供电公司 250100）

1 引言

随着风电场并入电网不断增加，风电场对电网稳定性的影响正逐渐显现[1,2]。特别是目前采用较多的 DFIG风电场并网，由于其与电网直接连接，一般情况下在电网故障时并网处电压跌落，当 DFIG不能承受并网处的电压跌落时，将会对 DFIG进行切机，电压跌落严重时DFIG风电场从并网处断开，进一步恶化电网的稳定性；因此，要求在电网故障时 DFIG风电场能够承受一定的电压跌落，并在故障后快速恢复电压，即DFIG风电场的低电压穿越[3]。

为了实现 DFIG的低电压穿越，常用的方法有增加变流器容量、改进变流器控制策略或者改进DFIG拓扑结构等[4,5]，或者在电网故障时在转子侧投入Crowbar使变流器闭锁[6,7]，同时防止转子过电流损坏变流器。投入Crowbar后DFIG运行于异步状态，DFIG风电场的特性发生变化。文献[2]对大规模风电连锁脱网事故进行了分析，指出电网故障时对风机转子侧使用Crowbar的重要性；但在DFIG风电场并网分析中没有考虑Crowbar的问题。

在风电场并网的研究中，常用一台或多台风电机组对风电场进行等值[8-14]。文献[8]利用集总参数将DFIG组成的80MW风电场等效为一台机组。文献[13]以发电机的转速为机群分类指标对异步定速风电场进行多机等值；文献[15]采用DFIG多机模型考虑不同运行状态风机的动态，但仍然无法反应各发电机的暂态变化。本文对电网故障时 DFIG的机理进行分析，根据 DFIG转子电流阈值，建立基于 Crowbar的 DFIG风电场双机等值模型，通过仿真验证了模型的准确性，在电网故障时采用快速无功补偿提高了DFIG风电场并网低压穿越能力。

2 基于Crowbar的DFIG风电场等值方法

2.1 DFIG的工作原理

DFIG模型由空气动力学模型、风力机轴系模型以及发电机模型三部分组成。

风速v下的机械功率为

式中，ρ为空气密度；v为风速；A为叶片扫掠面积；CP为风机的效率因子；λ为叶尖速比；β为桨距角。

二质块轴系模型的方程为

式中，HM、HG分别为风力机、发电机的惯性时间常数；TM、TE分别为风力机的机械转矩、发电机的电磁转矩；FM、FG分别为风力机和发电机的阻尼系数；ωM、ωG分别为风力机的叶轮、发电机的转子转速；ω0为发电机的同步转速；θS为质块间相对角位移。

发电机在dq坐标系下的电压方程表达式为

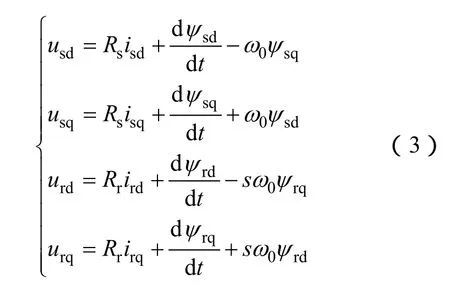
式中，usd、usq为发电机机端电压；isd、isq为定子电流；ψsd、ψsq为定子磁链；ird、irq为折算到定子侧的转子电流；ψrd、ψrq为转子磁链；Rs、Rr分别为定、转子电阻。

磁链方程

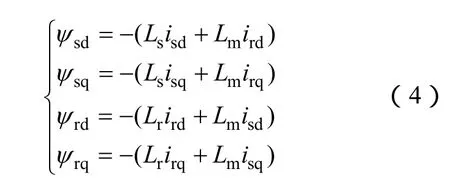
式中，Ls、Lr分别为定、转子电感；Lm为定、转子之间的互感。

电磁转矩方程

2.2 电网故障时DFIG转子侧电流大小的定量分析

对于DFIG，在电网故障时电网电压跌落瞬间，定子端电压急剧下降，此时定子磁链不突变，在定子中产生直流分量[16]，结果导致转子加速旋转、转子绕组过电流；此过电流会引起变流器的直流母线产生过电压损坏变流器。在电网故障发生时如果根据转子侧电流的阈值投入 Crowbar，即在转子侧投入Crowbar闭锁变流器，就会减小转子侧的电流。为了通过数学方法求解 DFIG的转子电流来决定是否投入 Crowbar，需要对 DFIG转子侧电流大小进行定量分析。

DFIG等效电路[17]如图1所示。

图1 DFIG等效电路Fig.1 The equivalent circuit of the DFIG

由图1可知转子侧电压的表达式

式中，ω1=ω0-ωr为转差角频率。

转子磁链表达式

式中，σ=1 -(LrLs)为漏磁系数。

将式（7）代入式（6）得

由式（8）可知，转子电压Ur的等式右边由两部分组成；前半部分只与定子磁链有关，后半部分只与转子电流有关。定义前半部分为

根据式（8）和式（9）将转子侧等效为如图 2所示电路。

图2 DFIG转子侧等效电路Fig.2 The equivalent circuit of DFIG rotor side

电网发生故障后机组端电压下降，设定子端电压由故障前US1降为US2。此时定子磁链不能突变[16,17]。

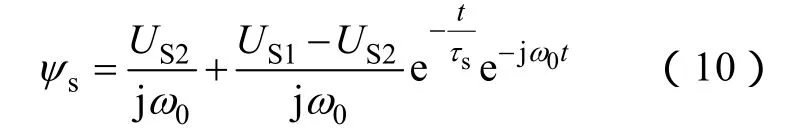
式中，τs=LsRs为定子时间常数。

代入式（9）得到

忽略定子电阻时有

对于转子侧变流器，假设能够按照控制策略跟踪控制转子电压，此时转子侧变流器的输出[17]

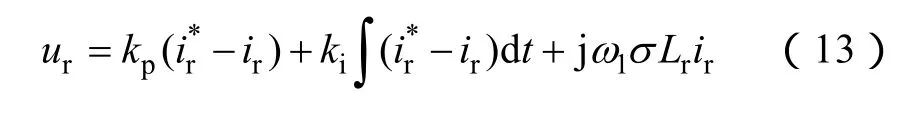
将式（13）、式（9）代入式（8）得到关于转子电流的微分方程为

当采用定子磁链定向控制时[18]，定子功率与转子电流关系为

定子磁链大小为

由最大功率追踪确定功率；DFIG以功率因数为 1运行时，Qs=0，风机的效率因子CP取典型值0.28，端电压跌落到US2得到DFIG转子电流有效值

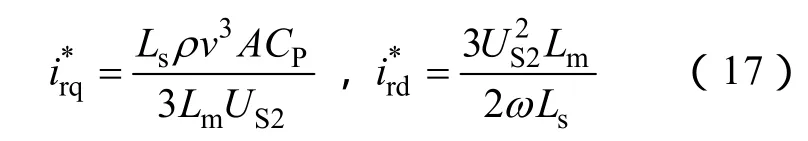
解微分方程式（14）得到转子电流表达式

由式（18）可知，转子侧电流的大小与电网故障前后电压都有关系，即电网故障电压以及 DFIG的运行状态有关。

2.3 DFIG风电场双机等值模型

当电网出现故障时，风电场并网处的各 DFIG端电压降低。在工程实践中一般采用硬件结构测量转子电流；当转子瞬态电流幅值超过其额定电流值的2倍时[19]，投入Crowbar保护DFIG中的变流器。风电场中的一部分DFIG投入Crowbar保护后就会使风电场整体特性发生变化。显然，直接有效的办法是对已投入、没有投入Crowbar的DFIG风电场分为两组分别进行等值。利用电网故障时风电场各机端的电压值求解 DFIG的转子电流；当求解的转子电流幅值超过额定值的2倍时，相应的DFIG划归到投入 Crowbar的一组，而未投入 Crowbar的DFIG划归为另一组，由此确定两组DFIG的数量。

根据确定的两组 DFIG，分别按照容量加权的方法进行等值，求得等值风机的电量及参数，建立DFIG风电场双机等值模型。容量加权等值方法是将多台风电机组等值为单台风电机组，机组的容量为所有容量之和；等值风电机组的电气量及参数的计算方法[20]如下

式中，下标eq代表等值符号；Si、Pi分别为第i台发电机视在功率和有功功率；Ci为第i台风机效率因子；Hi、Ki、Fi为第i台轴系参数；ZG为发电机的阻抗；vi第i台为风速；m为风电机组的台数。

在暂态分析中一般不考虑风速的变化，但 DFIG风电场等值应该反映风速在各个风电机组的分布情况，因此风速模型采用计及尾流效应的 Jensen模型[21]。

3 DFIG风电场双机等值模型并网仿真分析

3.1 DFIG风电场双机等值模型算例分析

在 WSCC9节点系统中接入 DFIG风电场，如图3所示。其中风电场为 5排5列的DFIG，排列整齐并以电缆相连，汇总到升压变压器母线，经过升压变压器升到 220kV，并经过 20km传输线连接到WSCC9节点系统的Bus5上。单台风机容量为2MW，额定电压690V，发电机的参数：Rs=0.001 64Ω，Ls=0.096mH，Rr=0.002Ω，Lr=0.095 5mH，Lm=2.87mH。

图3 WSCC9节点系统接入DFIG风电场Fig.3 WSCC 9-bus system with DFIG wind farm integration

稳态情况下求解各DFIG的端电压值US1；通过风电场外部潮流计算，得到风电场并网点端电压；进行风电场潮流计算得到各机端电压。在如图4中所示的风向下，风速为 12m/s，根据尾流效应的Jensen模型[21]，取机械功率转换效率为0.94，计算得到各DFIG的端电压值，见表1。

表1 正常运行DFIG端电压US1Tab.1 DFIG normal operation voltageUS1

图4 风电场DFIG排列Fig.4 Layout of the DFIG wind farm

在Line2靠近Bus5的22%处发生三相短路故障时，经过短路计算得到电网故障时各 DFIG电压跌落值US2，见表2。

表2 电网故障时DFIG电压跌落值US2Tab.2 Voltage dipUS2of DFIG during grid fault

将表1和表2电压代入2.2节中的DFIG转子电流表达式（18），得到电网故障时各DFIG的转子电流值。其中W25的转子电流波形如图5所示。

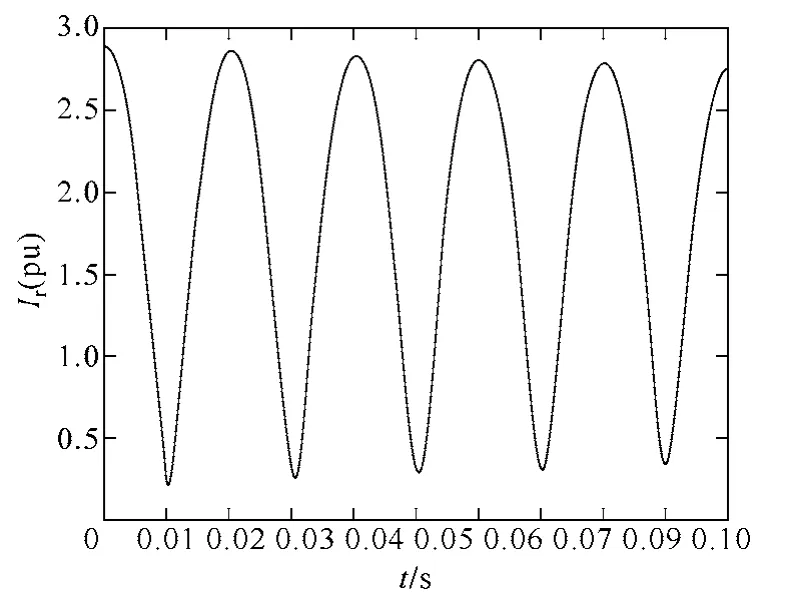
图5 电网故障时W25转子电流波形Fig.5 Calculated rotor current waveform of W25during grid fault

根据2.3节的要求，求出投入Crowbar的DFIG数量和位置；投入 Crowbar的分别是 w15、w23、w24、w25、w31、w32、w33、w34、w35、w43、w44、w45和w55共13台。

按照投入Crowbar情况将DFIG分成两组；每组采用各自的平均风速得到风电场双机等值模型，其容量分别为 26MW 机组和24MW 机组；其中26MW机组在电网故障过程中投入了Crowbar。

相应 DFIG风电场等值机组的电量及参数采用式（19）进行求解。本例采用完全相同的风机类型，各DFIG等值参数的标幺值不变。其中投入crowbar等值风机的风速为 11.34m/s，另一等值风机的风速为 11.42m/s。

3.2 DFIG风电场双机等值模型并网分析

采用仿真工具 PSCAD/EMTDC4.2.1 Professional，分别对DFIG风电场的单机等值模型和双机等值模型接入 WSCC9节点系统进行仿真，如图 6所示。

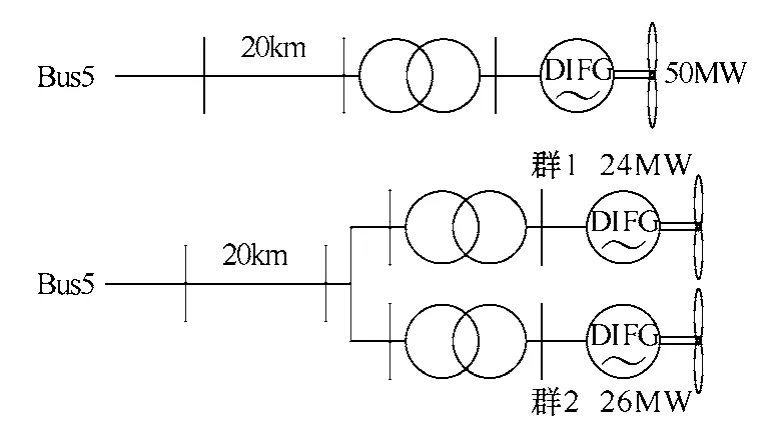
图6 仿真系统图Fig.6 Diagrams of the simulation system

若距离母线Bus5的22%处发生三相短路故障，仿真得到风电场电压的波形、无功功率和有功功率的波形曲线，分别如图7、图8和图9所示。

图7 DFIG风电场单机等值、双机等值并网点电压Fig.7 Voltage of DFIG wind farm one machine and two machine model to the grid at the connection during grid fault

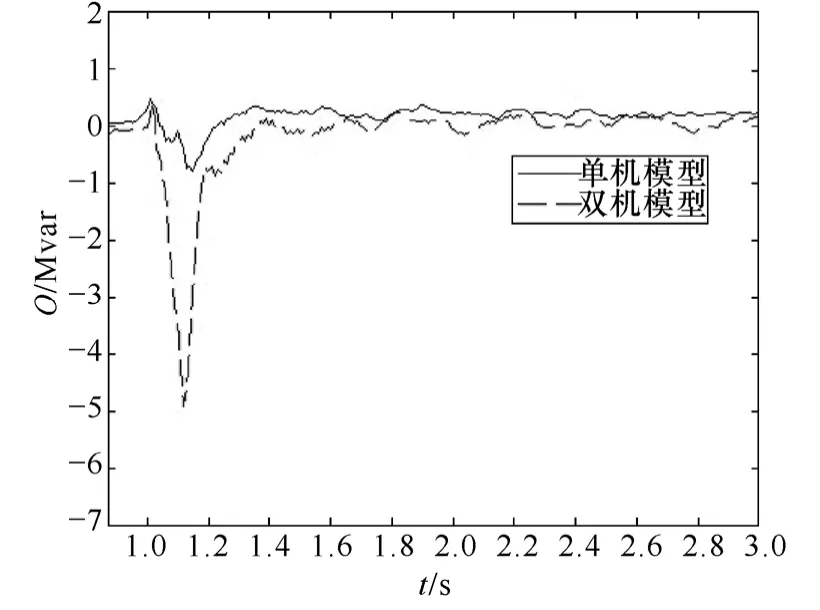
图8 DFIG风电场单机等值、双机等值无功功率Fig.8 Reactive power of DFIG wind farm one machine and two machine model during grid fault

图9 DFIG风电场单机等值、双机等值有功功率Fig.9 Active power of DFIG wind farm one machine and two machine model during grid fault

由仿真结果可知，双机等值模型能够更准确地反应电网故障时风电场的特性；单机模型与双机模型的并网点电压下降差距不大，主要原因是风电场容量相对于系统容量较小。双机模型在电网故障时的无功功率出现下降，这是因为风电场中的部分DFIG在电网故障时投入 Crowbar，在短暂时间内DFIG运行在异步状态，从系统中吸收无功功率，风电场双机等值模型准确地反映了这种变化。

4 提高风电场的低电压穿越能力

投入 Crowbar后转子侧变流器闭锁，DFIG运行在异步状态，从系统吸收无功功率，需要考虑在投入 Crowbar时进行无功功率的补偿，满足整个DFIG风电场的低电压穿越的要求，实现风电场在电网故障时持续并网。

文献[19]介绍了在暂态电压支撑方面 STATCOM与SVC相比具有响应速度快、不受并网点电压的限制等优点，选择STATCOM对风电场进行无功补偿。

图10 接有STATCOM的系统仿真示意图Fig.10 The diagram of simulation system with STATCOM

在风电场双机等值模型并网点接入 20MW 的STATCOM后进行仿真，接入与未接入STATCOM的电压波形如图11所示。接入STATCOM后的电压降落值为 0.497，并且电压恢复速度加快，接入STATCOM起到了较好的电压支撑作用。

图11 接入STATCOM前后DFIG风电场并网点电压Fig.11 Voltage comparison of DFIG wind farm with and without STATCOM

图12为接入和未接入STATCOM的风电场输出无功功率。由图 12可知，在电网故障时依靠STATCOM 的快速动态补偿，风电场能够向系统供给一定的无功功率。

综合上述分析，通过配置STATCOM，DFIG风电场的低电压穿越能力得到提高。

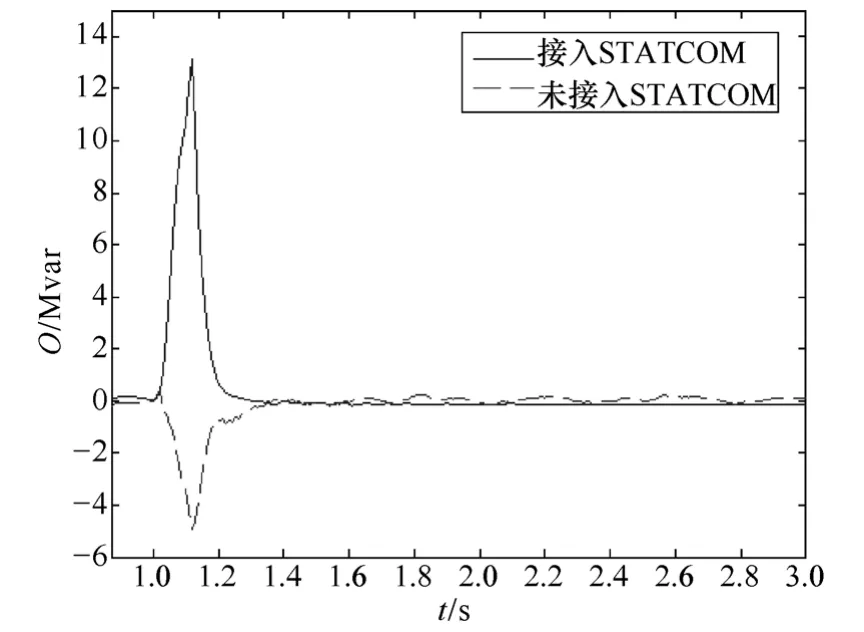
图12 接入STATCOM前后DFIG风电场输出无功功率Fig.12 Reactive power comparison of DFIG wind farm with and without STATCOM

5 结论

通过对电网故障时 DFIG转子电流特性进行机理分析，以 DFIG转子侧电流的阈值判断投入Crowbar，将DFIG风电场分为两组，建立了DFIG风电场双机等值模型。算例仿真，验证了提出方法的有效性；DFIG风电场双机等值模型能够较准确地反映电网故障时风电场的特性，特别是电网故障期间部分风机投入 Crowbar所引起的风电场的变化。采用快速无功补偿提高了 DFIG风电场的低电压穿越能力。

[1] Ullah N R,Thiringer T,Karlsson D. Voltage and transient stability support by wind farms complying with the E. ON Netz grid code[J]. IEEE Transactions on Power Systems,2007,22(4): 1647-1656.

[2] 叶希,鲁宗相,乔颖,等. 大规模风电机组连锁脱网事故机理初探[J]. 电力系统自动化,2012,36(8):11-17.

Ye Xi,Lu Zongxiang,Qiao Ying,et al. A primary analysis on mechanism of large scale cascading tripoff of wind turbine generators[J]. Automation of Electric Power Systems,2012,36(8): 11-17.

[3] 贺益康,周鹏. 变速恒频双馈异步风力发电系统低电压穿越技术综述[J]. 电工技术学报,2009,24(9):141-146.

He Yikang,Zhou Peng. Overview of the low voltage ride-through technology for variable speed constant frequency doubly fed wind power generation systems[J]. Transactions of China Electrotechnical Society,2009,24(9): 141-146.

[4] 李建林,许洪华. 风力发电系统低电压运行技术[M]. 北京: 机械工业出版社,2008.

[5] Sheng Hu,Xinchun Lin,Yong Kang,et al. An improved low-voltage ride-through control strategy of doubly fed induction generator during grid faults[J].IEEE Transactions on Power Electronics,2011,26(12):3653-3665.

[6] Vidal J,Abad G,Arza J,et al. Single-phase DC Crowbar topologies for low voltage ride through fulfillment of high-power doubly fed induction generator-based wind turbines[J]. IEEE Transactions on Energy Conversion,2013,28(3): 768-781.

[7] Sulla F,Svensson J,Samuelsson O. Short-circuit analysis of a doubly fed induction generator wind turbine with direct current chopper protection[J]. Wind Energy,2013,16(1): 37-49.

[8] Li Wang,Chia-Tien Hsiung. Dynamic stability improvement of an integrated grid-connected offshore wind farm and marine-current farm using a STATCOM[J].IEEE Transactions on Power Systems,2011,26(2):690-698.

[9] Shafiu A,Anaya-Lara O,Bathurst G. Aggregated wind turbine models for power system dynamic studies[J].Wind Engineering,2006,30(3): 171-186.

[10] Trudnowski D J,Gentile A,Khan J M. Fixed-speed wind-generator and wind-park modeling for transient stability studies[J]. IEEE Transactions on Power Systems,2004,19(4): 1911-1917.

[11] 孙建锋,焦连伟,吴俊玲,等. 风电场发电机动态等值问题的研究[J]. 电网技术,2004,28(7): 58-61.

Sun Jianfeng,Jiao Lianwei,Wu Junling,et al. Research on multi-machine dynamic aggregation in wind farm[J]. Power System Technology,2004,28(7): 58-61.

[12] Li H,Yang C,Zhao B,et al. Aggregated models and transient performances of a mixed wind farm with different wind turbine generator systems[J]. Electric Power Systems Research,2012,92(11): 1-10.

[13] 米增强,苏勋文,杨奇逊,等. 风电场动态等值模型的多机表征方法[J]. 电工技术学报,2010,25(5):162-169.

Mi Zengqinag,Sun Xunwen,Yang Qijun. Multimachine representation method for dynamic equivalent model of wind farms[J]. Transactions of China Electrotechnical Society,2010,25(5): 162-169.

[14] Vladislav Akhmatov,Hans Knudsen. An aggregate model of a grid-connected,large-scale,offshore wind farm for power stability investigations—importance of windmill mechanical system[J]. International Journal of Electrical Power & Energy Systems,2002,24(9):709-717.

[15] 米增强,苏勋文,余洋,等. 双馈机组风电场动态等效模型研究[J]. 电力系统自动化,2010,34(17):72-76.

Mi Zengqinag,Sun Xunwen,Yu Yang. Study on dynamic equivalence model of wind farms with turbine driven doubly fed induction generator[J]. Automation of Electric Power Systems,2010,34(17): 72-76.

[16] Mohsen Rahimi,Mostafa Parniani. Grid-fault ridethrough analysis and control of wind turbines with doubly fed induction generators[J]. Electric Power Systems Research,2010,80(2): 184-195.

[17] Lopez J,Sanchis P,Roboam X,et al. Dynamic behavior of the doubly fed induction generator during three-phase voltage dips[J]. IEEE Transactions on Energy Conversion,2007,22(3): 709-717.

[18] 贺益康,胡家兵,徐烈. 并网双馈异步风力发电机运行控制[M]. 北京: 中国电力出版社,2011.

[19] 迟永宁. 大型风电场接入电网的稳定性问题研究[D]. 北京: 中国电力科学研究院,2006.

[20] Shafiu A,Anaya-Lara O,Bathurst G. Aggregated wind turbine models for power system dynamic studies[J].Wind Engineering,2006,30(3): 171-186.

[21] Hagkwen Kim,Chanan Singh,Alex Sprintson. Simulation and estimation of reliability in a wind farm considering the wake effect[J]. IEEE Transactions on Sustainable Energy,2012,3(2): 274-282.