改善微电网频率稳定性的分布式逆变电源控制策略

孟建辉 石新春 王 毅 付 超 李 鹏

（华北电力大学新能源电力系统国家重点实验室 保定 071003）

1 引言

近年来，基于电力电子逆变接口的分布式能源（Distributed Energy Resources，DER）在电力系统中所占比重增长迅速，许多国家和地区均制定了各自的分布式能源发展计划[1,2]。其大量接入会对整个电力系统的动态响应及稳定性造成影响[3]，为了降低其给系统带来的不利影响，最大程度上提高DER的利用率，将 DER接入微电网独立运行或继而接入配电网运行，是提高DER利用率的有效方式之一[4-6]。

微电网通常是由柴油发电机、DER、储能装置、负荷、变流器及监控保护装置等共同组成的小型发配电系统[7,8]。其中，柴油发电机可以作为整个系统的平衡节点，以支撑系统的电压和频率。但是由于整个微电网系统的转动惯量较小，是一弱电网系统，当微电网系统独立运行且 DER接入较多时其频率稳定性能较差，因为转动惯量反映了系统阻止频率突变的能力，是保证系统频率稳定的重要因素之一。所有的同步发电机（Synchronous Generator，SG）组及部分电动机负荷可以对系统的转动惯量提供支持，而DER是无旋转的静止元件，通过变流器并网，无旋转惯量[9,10]。针对该问题，国内外的学者提出通过改变DER逆变电源的控制策略，向系统注入虚拟的转动惯量，使DER逆变电源模拟出类似同步发电机所具有的旋转惯性和阻尼特性，即虚拟同步发电机（Virtual Synchronous Generator，VSG）控制方法[11]，有望成为 DER逆变电源接入系统的主流技术。

文献[11]首次提出了虚拟同步发电机的概念，该方案通过同步发电机的模型来控制逆变电源的输出电流，将其等效为受控电流源，对孤立微电网的适应性不强。文献[12]利用SG的数学模型，在有功功率和无功功率外环控制中加入频率调节器和电压调节器，实现了分布式逆变电源的电流型 VSG控制，但该算法中频率调节器使用一节延迟环节，并不能准确地反映出 SG的转子运动特性。文献[13]提出了能够运行在并网和自治两种模式的电压型VSG控制方法，该方法模拟了SG的转子和一次调频特性，提高了系统频率的稳定性，但该算法并未考虑 SG无功环节的延迟特性，且底层电压电流为非解耦控制，并网时控制参数不易设计，谐波较大。文献[14]根据SG的电磁方程、一次调频及调压控制特性提出的电压型 VSG控制算法，较好地模拟了SG的外特性，取得了良好的控制效果。此外，文献[15-19]针对 VSG算法的参数选择及相关应用进行了研究，均在不同程度上仿真验证了其相比于传统控制算法的优势。

本文在上述文献的基础上，首先通过理论分析及相关公式的推导阐明了 VSG控制在微电网系统中的重要作用。其次，针对DER逆变电源的控制策略，提出将 SG的转子运动方程、一次调频特性及无功调节延迟特性引入到逆变电源的上层控制中，底层控制则根据同步发电机并网矢量关系得到。最后为了验证所提 VSG控制策略对微电网系统频率稳定性的支持作用，搭建了简单微电网系统的Matlab/Simulink仿真模型，并根据实验室已有条件，设计了微电网的实验平台，对理论分析进行了仿真及物理实验验证。

2 微电网与VSG控制

2.1 含VSG控制的微电网结构

VSG通常由能量存储单元、逆变装置及相应的控制算法组成，本文在研究中假设系统配备有足够的储能装置，且自身的荷电状态能够满足系统对其的输出要求，研究重点放在 DER逆变电源本身的VSG控制策略上。含 VSG单元的简单微电网拓扑结构如图1所示，其中，T1～T4为交流变压器，KM表示静态开关。

蓄电池组及光伏阵列经直流升压装置升压后汇集到直流母线上，再经含 VSG控制的逆变单元及隔离变压器变换为交流电，从而与同步发电机及负载单元组成简单的微电网系统。该微电网拓扑结构可通过变压器与主电网相连，也可独立运行，本文重点考虑其不与主电网相连时的弱电网情况，系统的频率及电压依然由实际的同步发电机组来支撑，但DER在整个微电网系统中的穿透功率水平较高，以便测试系统发生频率波动时所提控制策略的作用及效果。

含 VSG控制的逆变单元连接在直流母线与交流母线之间，对于这样含大量DER的微电网系统有着极其重要的作用。因为该微电网结构下，系统的惯性较小，任何负荷的突然变化都会导致微电网系统的供需不平衡，从而改变同步发电机组的转速变化，进而影响到系统频率的稳定。然而，利用具备快速响应特性的 VSG装置可以减小由于负荷突变而造成的频率偏差，从而改善微电网的频率稳定性并提升DER自身的穿透功率水平。

2.2 VSG控制与频率稳定性

在传统电力系统中，当系统输出的功率与负荷消耗的功率不平衡时，便会产生功率差，此时同步发电机组转子机械部分存储的旋转动能会补偿这一偏差，从而造成同步发电机组转速下降，而系统的频率又是由 SG的转速决定的，则系统的频率会偏离原先的额定值。由于DER逆变电源本身不具有旋转动能，其穿透功率水平的提高必然会加大频率偏差的范围，因此有必要对VSG控制与系统频率稳定性的关系进行理论推导分析。

对于常规同步发电机组，其输出的功率与消耗的功率不平衡时，旋转动能Ek便会补偿这一偏差，其中偏差值ΔEk[20]可表示为

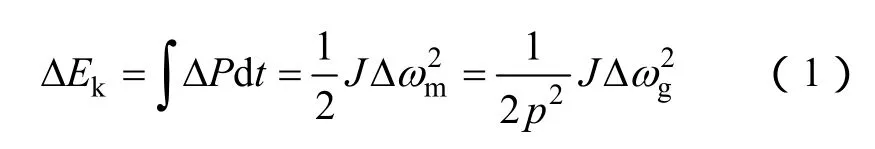
式中，ΔP为输出与消耗的功率差；ωm、ωg分别为SG的机械角频率和电角频率；J为转动惯量；p表示同步发电机的极对数，设极对数为1。由式（1）可得

假设该系统中有n个SG，则式（2）可变为

式中，Jt为系统总的转动惯量。

为了使DER逆变电源模拟出类似SG所具有的旋转惯量，可将其输出的有功功率与系统的频率变化建立一定的函数关系，从而使得DER逆变电源具有相应的虚拟惯量。而具有n个SG及m个VSG单元的有功功率与惯量（包括实际的转动惯量与虚拟惯量）之间的关系可表示为

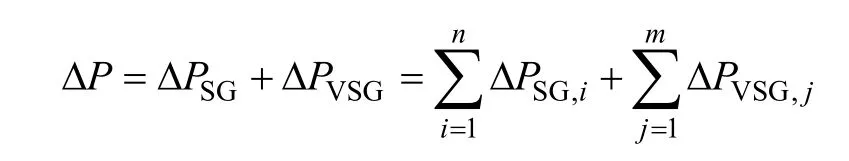
此时，系统总的惯量为

从式（5）可以看出，在包含SG与VSG单元的电力系统中，总的旋转惯量是由两者共同决定的。当DER大量接入到电力系统中时，SG总的旋转惯量相对减小，如果此时接入的DER逆变电源不具有旋转惯量，则系统总的旋转惯量减小，系统频率稳定性变差，进而影响到 DER自身接入到电力系统的穿透功率水平。然而，通过相应的控制策略及方法，使得大量接入的DER逆变电源转变为VSG单元，即包含虚拟的旋转惯量，则可以相对增加系统总的旋转惯量，提高系统的频率稳定性，进而也可提高DER接入电网的穿透功率水平。

3 DER逆变电源的VSG控制策略

3.1 SG矢量关系原理

为了能够使 DER逆变电源具有 SG的相似特性，首先对SG的相关原理进行说明。SG并网发电时的等效电路及电压电流相量关系如图2所示。图中，Us为 SG的内部电动势；R、jX分别为等效电阻及电抗；Ug为端电压，联网运行时也即并网电压；Ig为输出电流；φ为相位角。此处，设定旋转坐标系直轴 d的方向与网端电压Ug同相，交轴 q与 d轴垂直。

图2 SG并网等效电路及矢量关系图Fig.2 Grid-connected equivalent circuit and vector diagram of the SG

将图2中相关矢量分别在d轴及q轴上分解，可以得出输出电流在直轴和交轴上参考值的表达式为

其中，导纳Y及Usd、Usq分别为

相位角φ表示转子角速度ω与系统角速度ωg差值的积分，即

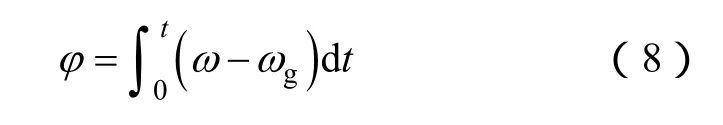
实际SG中，其转子角速度ω是由调速器决定的，与有功功率及角频率设定值有关；内部电动势Us是由励磁系统决定的，与无功功率及电压设定值相关。根据 SG相关原理，可以将其调速器模型及励磁系统模型融入到DER逆变电源的控制中，从而使其具有与SG相似的响应特性。

3.2 VSG控制算法

因同步发电机转子具备一定惯性，其频率在较短时间内不会发生突变，根据其转子运动方程[20,21]，将虚拟惯性控制引入到分布式逆变电源的控制算法中，从而模拟出同步发电机的转子运动特性，可得分布式逆变电源的有功频率控制方程为

式中，H为虚拟惯性时间常数，与转动惯量J相对应，是按照发电机额定基准规格化后的量，采用H表示较简便，详情参见文献[21]；Pin、Pout分别为逆变电源的输入和输出功率；ω、ωg分别为逆变电源及公共母线的角频率；Kd为阻尼系数。

当 DER逆变电源工作在并网模式且电网为强电网时，其频率ωg被钳位，无需DER逆变电源进行调频。但当 DER逆变电源工作在微电网这样的弱电网中时，需要分布式逆变电源具备一定的调频能力，以支持微电网系统的稳定。因此提出增加有功-频率下垂控制环节，构成调频控制器。即

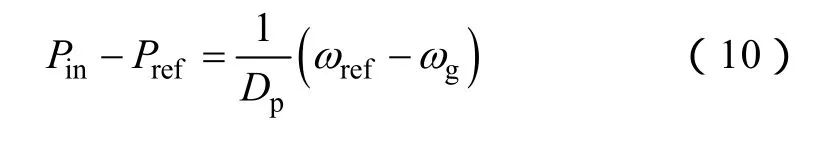
式中，Pref为有功功率输入设定值；Dp为有功功率的下垂系数；ωref为角频率的参考值。

此外，下垂系数Dp在选择时与传统控制算法相似，太小了会影响有功功率的调节精度，太大了会对系统的稳定性产生不利影响。因此在Dp的选择上既要考虑有功功率调节的精度，又要考虑微电网系统的稳定性，设计时可以采用小信号分析的方法。

联立式（9）和式（10）可得 DER逆变电源的“调速器”模型，即有功-频率控制器的传递函数为

则有功-频率控制框图如图3所示。

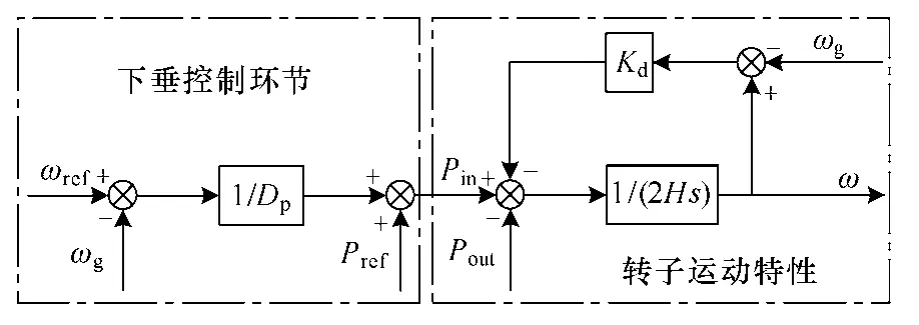
图3 有功-频率控制框图Fig.3 Active power-frequency control diagram

所设计的调频控制器可以在微电网频率波动时提供附加的功率，减小系统频率的波动。此外，阻尼控制模块Kd(ω-ωg)可以保证分布式逆变电源频率与微电网系统频率一致。

同样，与同步发电机励磁系统相似，设计DER逆变电源的无功-电压控制器如图 4所示。其中，Qref为无功功率输入设定值；Dq为无功功率的下垂系数；Ta为延迟环节的时间常数；Uset为DER逆变电源端压参考值；Ug为DER逆变电源的输出电压，并网运行时与系统母线电压一致；kp、ki为比例积分系数。

图4 无功-电压控制框图Fig.4 Reactive power-voltage control diagram

DER逆变电源的参考电压表达式为

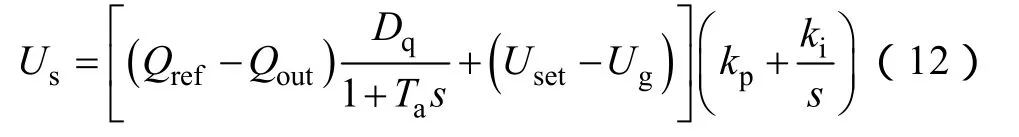
式中，下垂系数Dq决定了系统的无功-电压下垂特性；增加的一阶延迟环节，模拟了同步发电机励磁系统的调节过程，可使无功功率缓慢地过渡到新的稳态值，减小特定情况下其对系统的冲击；而 PI控制器用以保证输出电压的稳定。

此外，针对配有储能装置的分布式电源常采用的下垂控制策略[22]，其虽然模拟了SG的一次调频及部分励磁调节特性，但是并未模拟出 SG的转子运动特性，当其接入系统时频率稳定性能相对较差。这是由于转子具有惯性，当功率缺额时，转速将缓慢降低以释放动能，并在调速器的作用下达到新的稳态，因此其频率具有一定的抗扰动能力。而仅采用下垂控制策略时，逆变器的响应速度较快，扰动情况下频率变化迅速，对系统的频率稳定性不利。

3.3 DER逆变电源整体控制策略

提出的基于 VSG控制的分布式逆变电源整体控制策略如图5所示，为了更好地研究DER逆变单元的控制方法，忽略储能及分布式能源自身的动态响应特性，将其用直流电压源来代替。

图5 整体控制框图Fig.5 Overall control diagram

图5中，Udc为等效直流电压源；S1～S6为IGBT开关管；R、L、C分别为滤波电感内阻、滤波电感及滤波电容；Iabc表示输出的三相电流；Uabc为滤波电容三相电压，也即公共母线端电压；PLL（phase locked loop）为锁相环。

DER逆变电源在提出的基于 VSG控制策略下工作时，系统会首先根据中央控制器的指令得到有功功率及无功功率的参考值，经有功-频率及无功-电压控制模型后分别输出角频率及电压参考值，再根据同步发电机的矢量关系得到输出电流分别在旋转坐标系d轴和q轴分量上的参考值，分别与实际测量值比较后经 PI控制器及坐标反变换后驱动PWM发生器产生脉冲来控制开关管的通断。此外，实际电压角频率及相角的测量是通过PLL得到的。

据以上理论推导及分析可得，通过 SG转子运动方程、无功电压特性及相关的相量关系原理，将DER逆变电源的输出功率与频率、无功功率与电压建立了一定的函数关系，使得DER逆变电源具备了虚拟的转动惯量，这种控制策略下的DER逆变电源再接入到微电网系统时便可以增加系统总的旋转惯量，从而为改善微电网系统频率的稳定性做出贡献。

4 仿真分析

4.1 仿真系统概述

为了验证所提出的 VSG控制策略，本文利用Matlab/Simulink仿真软件搭建了如图1所示的微电网仿真系统平台，其中实际的同步发电机组包含G1和G2两个，其容量大小分别为16kV·A、8.1kV·A，G1作为系统的平衡节点，来支撑整个微电网系统的电压和频率，且具备二次调频能力。G2有功输出一定，不承担系统的调频任务。DER逆变电源额定容量为5kV·A，负载Ld为恒定有功负荷，容量为10kW。其中，系统的仿真参数详见附录。

仿真时，将采用传统解耦控制算法[23]及本文所提VSG控制算法下的DER逆变电源分别接入所搭建的微电网系统进行对比分析。仿真过程设置如下：初始时刻，光伏电源运行在最大功率跟踪状态，其光照强度为470kW/m2，G1、G2及DER逆变电源的输出功率分别为 3.5kW、2kW 及 2kW，负载Ld为7.5kW，系统稳定运行，5s时通过增减负载Ld的大小来观测整个微电网系统的动态响应。

4.2 负载突增下的仿真分析

图 6和图 7所示为负载Ld在 5s时突增1.5kW情况下的频率响应及功率响应对比结果。

图6 负载Ld突增1.5kW时系统的频率响应对比Fig.6 Comparison of the network frequency response during loadLdsudden increasing of 1.5kW

图6中，负载由7.5kW突增至9kW，DER逆变电源采用VSG控制算法时，微电网系统的频率变化得到了明显减缓，频率的最小值由传统控制算法下的 49.28Hz上升为 49.60Hz，频率的幅值变化减少了44.4%，基于VSG控制算法下的DER逆变电源在频率变化的动态过程中对整个微电网系统起到了显著的惯性支持作用。

图7 负载Ld突增1.5kW时DER逆变电源、G1及G2的有功功率响应对比Fig.7 Comparison of the active power response of DER inverter、G1and G2duringLdsudden increasing of 1.5kW

图 7对比了 DER逆变电源采用传统控制及VSG控制组网时系统中各个微源的功率响应特性。

在DER逆变电源采用传统控制时，其本身不具备旋转惯性，频率变化基本不会影响到其功率的输出值。同步发电机 G1作为整个微电网系统的平衡节点，负荷Ld的突增导致 G1的有功功率输出快速增加，因原动机的功率调节速度较慢，导致同步发电机的功率不平衡，转速下降，进而系统的频率减小。此时，G2的有功功率输出在频率变化瞬间波动较大。而当DER逆变电源采用所提VSG控制算法时，其本身具备了一定的虚拟惯性，在微电网中负荷的功率突变时，会对系统突变的功率有一定的分担，进而缓解 G1的功率不平衡情况，从而降低了系统频率的变化幅值。此外，从G2的有功功率响应对比曲线可以看出，VSG控制时，其功率输出波动的幅值较小，且进入稳定状态的速度更快。

4.3 负载突减下的仿真分析

图 8和图 9所示为负载 Ld在 5s时突减 1.5kW情况下的频率响应及功率响应对比结果。

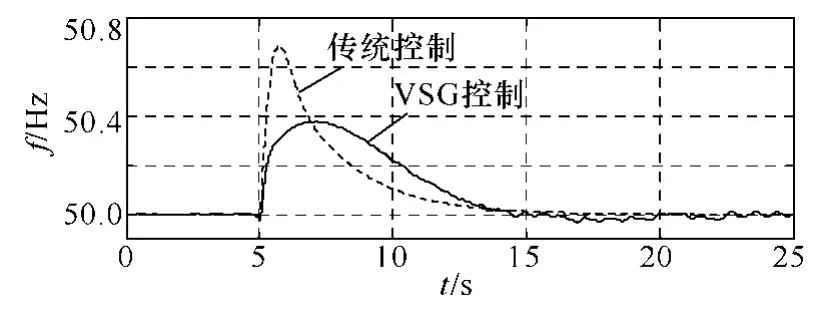
图8 负载Ld突减1.5kW时系统的频率响应对比Fig.8 Comparison of the network frequency response during loadLdsudden decreasing of 1.5kW

图9 负载Ld突减1.5kW时DER逆变电源、G1及G2的有功功率响应对比Fig.9 Comparison of the active power response of DER inverter、G1and G2duringLdsudden decreasing of 1.5kW

图8中，负载由7.5kW突减至6kW，DER逆变电源采用VSG控制后，微电网系统频率的最大值由 50.68Hz减小为 50.37Hz，频率的变化幅值减少了45.5%，从而改善了系统频率的动态响应。

图9为DER逆变电源、同步机发电机G1和G2的功率响应对比，可以看出，DER逆变电源采用所提 VSG控制时，G1有功功率输出的变化率明显减小，从而在很大程度上缓解了微电网系统频率的变化，提高了系统频率的稳定性。此外，G2的有功功率输出波动减小，且快速地达到稳定。

4.4 不同惯性时间常数下的对比分析

图10对比了不同惯性时间常数H下微电网系统在负载Ld突增1.5kW时的动态响应特性。

图10H变化下负载Ld突增1.5kW时系统的动态响应Fig.10 Dynamic response during loadLdsudden increasing of 1.5kW with the change ofH

可以看出，针对DER逆变电源采用VSG控制策略后，均可以在不同程度上减小系统频率的变化范围。虚拟惯性时间常数H取值不同，在频率动态调节的过程中DER逆变电源将表现出不同的惯性，即DER逆变电源虚拟出的惯性越大，对微电网系统频率的支持作用越明显。但是随着H的增加，DER逆变系统的动态响应缓慢，超调量变大，逐渐会产生一定的振荡。因此，在惯性时间常数H的选择上，应综合微电网系统的整体要求及每个微源自身的响应特性，并考虑DER逆变电源的动态响应时间、超调量及达到稳定所需时间等。此外，在DER容量适当的情况下，通过改变不同的惯性时间常数可以虚拟不同的惯性大小，展现了其相比于实际同步发电机灵活多变的优势。

4.5 三种控制策略的对比分析

图11对比了针对DER逆变电源采用传统控制、下垂控制及VSG控制下负载Ld在5s时突增1.5kW情况下的频率响应特性。

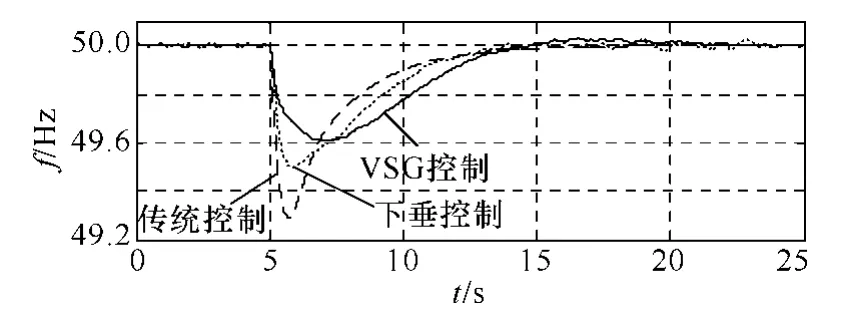
图11 三种控制策略下系统频率响应对比Fig.11 Comparison of the network frequency response under three control strategies

从图11可以看出：负载突增后，相比于传统控制，采用下垂控制及VSG控制均能在一定程度上减小频率下降的幅值；下垂控制时，系统频率的下降速度较快，响应迅速，而VSG控制下，频率则缓慢下降，这是由于虚拟的转子惯性延缓了频率的下降速度，一段时间后，系统频率才由平衡节点G1调节至额定频率，因此相比于传统控制及下垂控制，VSG控制提高了系统频率的稳定性。

5 实验验证

为了充分验证所提 VSG控制策略对微电网系统稳定性的支持作用，根据图1所示拓扑结构，搭建了简单微电网实验平台。该实验平台主要包含两台通过异步电动机拖动的额定容量为6.8kV·A的同步发电机、10kW的交流可调负载以及5kW的DER逆变电源等。其中同步发电机的特性模拟是通过西门子S7—200型PLC控制ACS550变频器，进而控制异步电动机拖动同步发电机来实现的，包含单晶光伏及铅酸储能的 DER逆变电源是通过切换盘及并机装置并入网微电网系统中的。

DER逆变电源的核心控制器采用 TI公司的TMS320F28335，功率开关管IGBT采用Infineon公司的FF450R12ME4，其驱动模块采用Concept公司的 2SC018T2A0—17，实验波形及数据的采集使用Yokogawa公司的 DL850示波记录仪及 NI公司的cRIO—9025控制器及相关数据分析采集卡。此外，为了缩短VSG控制算法的实验验证时间，最大程度上保证仿真算法和实际应用的一致性，根据已经搭建的Matlab/Simulink仿真控制模型，利用eZdsp配置好DSP的资源及端口，实现了对仿真模型的快速控制程序代码的自动生成。

考虑到实际装置的容量及整个微电网系统的安全性，设定稳态运行时负荷为 5kW，同步发电机G1和G2各承担2kW，DER逆变电源输出1kW，某一时刻突增负荷 1kW，分别测试 DER逆变电源采用传统控制及 VSG控制时整个微电网系统的动态响应，其结果如图12和图13所示。

图12a和图13a为两种控制算法下的电压电流波形，均为相电压、相电流，共记录了20s的波形。图 12b、图 13b为不同控制算法下微电网的系统频率及各微源的功率波形，可以看出，采用VSG控制时，系统的频率幅值变化明显减缓，这是由于系统突增负荷的瞬间，DER逆变电源对突增的功率有所分担，从而减缓了同步发电机 G1输出功率的变化率，使得频率变化幅值的最小值有所降低，从而提高了整个微电网系统频率的稳定性。

图13 VSG控制下负荷突增1kW时系统的动态响应Fig.13 System dynamic response during load L sudden increasing of 1kW under the VSG control

此外，同仿真分析结果一样，VSG控制下，同步发电机 G2的功率波动范围减小，且恢复稳定时间缩短。突减负荷下的实验同样可以得出相似的结论，限于篇幅，不再给出。

以上实验充分验证了本文所提出的 VSG控制策略应用在DER逆变电源上，可以提高微电网系统的动态稳定性，是提高DER在微电网乃至整个电力系统穿透功率水平的重要方法之一。

6 结论

本文在理论上推导并分析了虚拟同步发电机控制与微电网频率稳定性的关系，研究了一种基于虚拟同步发电机的分布式逆变电源整体控制策略，通过数字仿真及物理实验平台验证，得出如下结论：

（1）随着分布式能源在微电网乃至整个电力系统中穿透率的不断上升，系统的转动惯量不断下降，导致系统的动态频率响应及暂态稳定性不断恶化。

（2）利用 SG的转子运动方程、一次调频特性及无功电压调节、无功延迟特性构造的VSG控制策略，较好地模拟了同步发电机的特性，将微电网系统的频率变化和DER逆变电源的输出功率变化联系起来，使得系统总的惯量增加，提高了微电网的频率稳定性。

（3）通过搭建的简单微电网物理实验平台，对含基于VSG控制的DER逆变电源的微电网系统进行的实验验证，更好地说明了其实际应用价值。

（4）对于未来大规模分布式能源接入整个大的电力系统提供了一种解决方案。

附录 仿真系统参数

附表1 DER逆变电源参数App. Tab.1 Parameters of the DER inverter

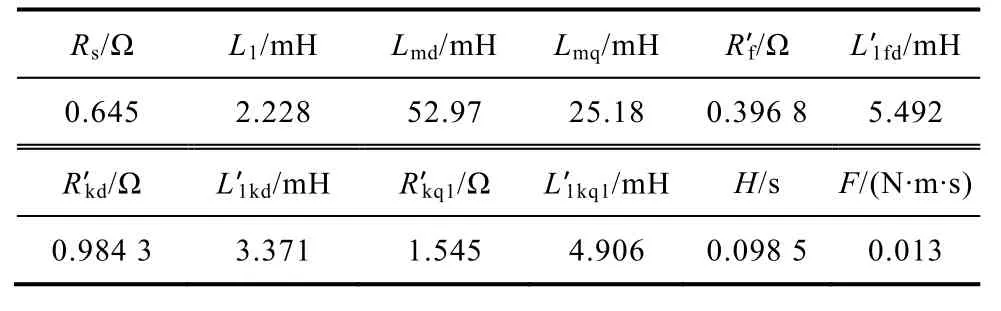
附表2 同步发电机G1参数App. Tab.2 Parameters of the G1

附表3 同步发电机G2参数App. Tab.3 Parameters of the G2

[1] Solangi K H,Islam M R,Saidur R,et al. A review on global solar energy policy[J]. Renewable and Sustainable Energy Reviews,2011,15(4): 2149-2163.

[2] Tan W S,Hassan M Y,Majid M S,et al. Optimal distributed renewable generation planning: A review of different approaches[J]. Renewable and Sustainable Energy Reviews,2013,18: 626-645.

[3] 李霞林,郭力,王成山. 微网主从控制模式下的稳定性分析[J]. 电工技术学报,2014,29(2): 24-34.

Li Xialin,Guo Li,Wang Chengshan. Stability analysis in a master-slave control based microgrid[J]. Transactions of China Electrotechnical Society,2014,29(2):24-34.

[4] 王成山,武震,李鹏. 微电网关键技术研究[J]. 电工技术学报,2014,29(2): 1-12.

Wang Chengshan,Wu Zhen,Li Peng. Research on key technologies of microgrid[J]. Transactions of China Electrotechnical Society,2014,29(2): 1-12.

[5] 沈沉,吴翔宇,王志文,等. 微电网实践与发展思考[J]. 电力系统保护与控制,2014,42(5): 1-11.

Shen Chen,Wu Xiangyu,Wang Zhiwen,et al. Practice and rethinking of microgrids[J]. Power System Protection and Control,2014,42(5): 1-11.

[6] 周林,黄勇,郭珂,等. 微电网储能技术研究综述[J]. 电力系统保护与控制,2011,39(7): 147-152.

Zhou Lin,Huang Yong,Guo Ke,et al. A survey of energy storage technology for micro grid[J]. Power System Protection and Control,2011,39(7): 147-152.

[7] Hatziargyriou N,Asano H,Iravani R,et al. Microgrids[J]. IEEE Power and Energy Magazine,2007,5(4): 78-94.

[8] 张建华,于雷,刘念,等. 含风/光/柴/蓄及海水淡化负荷的微电网容量优化配置[J]. 电工技术学报,2014,29(2): 102-112.

Zhang Jianhua,Yu Lei,Liu Nian,et al. Capacity configuration optimization for island microgrid with wind/photovoltaic/diesel/storage and seawater desalination load[J]. Transactions of China Electrotechnical Society,2014,29(2): 102-112.

[9] 曾正,赵荣祥,汤胜清,等. 可再生能源分散接入用先进并网逆变器研究综述[J]. 中国电机工程学报,2013,33(24): 1-12.

Zeng Zheng,Zhao Rongxiang,Tang Shengqing,et al.An overview on advanced grid-connected inverters used for decentralized renewable energy resources[J].Proceedings of the CSEE,2013,33(24): 1-12.

[10] 丁明,王伟胜,王秀丽,等. 大规模光伏发电对电力系统影响综述[J]. 中国电机工程学报,2014,34(1): 1-14.

Ding Ming,Wang Weisheng,Wang Xiuli,et al. A review on the effect of large-scale PV generation on power systems[J]. Proceedings of the CSEE,2014,34(1): 1-14.

[11] Beck H P,Hesse R. Virtual synchronous machine[C].9th International Conference on Electrical Power Quality and Utilisation. Barcelona,Spain: IEEE,2007:1-6.

[12] Hirase Y,Abe K,Sugimoto K,et al. A grid connected inverter with virtual synchronous generator model of algebraic type[J]. IEEJ Transactions on Power and Energy,2012,132(4): 371-380.

[13] Gao F,Iravani M R. A control strategy for a distributed generation unit in grid-connected and autonomous modes of operation[J]. IEEE Transactions on Power Delivery,2008,23(2): 850-859.

[14] Zhong Q C,Weiss G. Synchronverters: Inverters that mimic synchronous generators[J]. IEEE Transactions on Industrial Electronics,2011,58(4): 1259-1267.

[15] 吕志鹏,罗安,蒋雯倩,等. 多逆变器环境微网环流控制新方法[J]. 电工技术学报,2012,27(1): 40-47.

Lü Zhipeng,Luo An,Jiang Wenqian,et al. New circulation control method for micro-grid with multiinverter micro-sources[J]. Transactions of China Electrotechnical Society,2012,27(1): 40-47.

[16] 杜威,姜齐荣,陈蛟瑞. 微电网电源的虚拟惯性频率控制策略[J]. 电力系统自动化,2011,35(23):26-31.

Du Wei,Jiang Qirong,Chen Jiaorui. Frequency control strategy of distributed generations based on virtual inertia in a microgrid[J]. Automation of Electric Power Systems,2011,35(23): 26-31.

[17] 王思耕,葛宝明,毕大强. 基于虚拟同步发电机的风电场并网控制研究[J]. 电力系统保护与控制,2011,39(21): 49-54.

Wang Sigeng,Ge Baoming,Bi Daqiang. Control strategies of grid-connected wind farm based on virtual synchronous generator[J]. Power System Protection and Control,2011,39(21): 49-54.

[18] Sakimoto K,Miura Y,Ise T. Stabilization of a power system with a distributed generator by a virtual synchronous generator function[C]. IEEE 8th International Conference on Power Electronics and ECCE Asia,The Shilla Jeju,Korea,2011: 1498-1505.

[19] Linn Z,Miura Y,Ise T. Power system stabilization control by HVDC with SMES using virtual synchronous generator[J]. IEEJ Journal of Industry Applications,2012,1(2): 102-110.

[20] 倪以信,陈寿孙,张宝霖. 动态电力系统的理论和分析[M]. 北京: 清华大学出版社,2002.

[21] Anderson P M,Fouad A A. 电力系统控制与稳定[M]. 王奔,译. 北京: 电子工业出版社,2012.

[22] 王成山. 微电网分析与仿真理论[M]. 北京: 科学出版社,2013.

[23] Vladimir Blasko,Vikram Kaura. A new mathematical model and control of a three-phase AC-DC voltage source converter[J]. IEEE Transaction on Power Electronics,1997,12(1): 116-123.