电压型PWM整流器无差拍预测直接功率控制

叶虹志 姜 燕 黄守道 肖 磊 廖 武

（1. 湖南大学电气与信息工程学院 长沙 410082 2. 南车电气技术与材料工程研究院 株洲 412000）

1 引言

PWM 整流器因其诸多优点在各类变流装置中取得了广泛而重要的应用，主要表现在网侧呈现出受控电流源特性、可单位功率因数运行以及能量可双向流动等[1]。

近年来，关于 PWM整流器的控制技术，一种基于瞬时功率理论的直接功率控制策略（Direct Power Control，DPC）受到许多学者的关注和研究。DPC根据功率滞环比较器的输出查找开关表选择合适的矢量对有功功率和无功功率实现解耦控制，具有算法简单、功率响应快速等优点。但其主要缺点是开关频率不固定，不便于输出滤波器的优化设计，并且对系统采样频率要求很高[2-4]。基于 PI调节的 DPC策略，采用空间矢量脉宽调制（Space Vector Pulse Width Modulation，SVPWM）技术调制目标电压矢量，实现了开关频率恒定，并且直流侧电压利用率高，电流谐波的畸变率较低，但该策略受电网电压角度信息影响较大，电网电压畸变、不平衡或谐波含量较大时控制性能不理想，甚至出现振荡[5,6]。基于 PI调节的固定开关频率虚拟磁链定向 DPC（VF-DPC）方法，可以有效滤除电压谐波以及电流纹波对磁链观测的影响，但存在积分漂移问题，同样影响电网电压矢量定向的准确度，并且积分以及 PI的引入降低了系统跟踪指令信号的快速性能[7,8]。

预测控制作为一种控制思想简单的控制方式受到了研究人员越来越多的关注，并被广泛应用于电力电子领域。被引入的预测控制方法主要有无差拍控制、跟踪控制和模型预测控制等[9-11]。比较典型的模型预测控制是根据系统的离散化预测模型，设定一个指标函数，在下一个离散周期选择使指标函数最小的控制方式，从而实现最优控制，但控制过程复杂，运算量仍然较大[12-14]。无差拍预测控制根据预测的下一拍给定值来控制当前系统，具有响应快速，控制精确的优点，但受A-D采样、数字运算等等所带来的控制延时影响较大，而且对系统参数敏感，容易造成系统不稳定[15,16]。

本文以三相电压源型 PWM整流器数学模型为基础，在两相静止坐标系下研究了一种无差拍预测直接功率控制策略，改进了无差拍预测控制对预测给定值的预测方法。文献[16]中将两个连续的采样周期预测给定值差值视为相等，预测方法线性、简单，但对系统给定指令的跟踪性能差，并且存在稳态误差。改进的无差拍预测直接功率控制方法无需电网电压矢量定向，并且为消除因预测方法缺陷，以及变量近似和控制延时所带来的影响，在推出的无差拍功率预测模型中引入基于内模原理的准积分环节进行反馈校正[17]，每一拍都修正预测给定值，来获得优化的功率跟踪性能，消除系统的稳态误差，使系统的稳定性和鲁棒性更高。

2 电压源型PWM整流器的数学模型

如图1所示为三相电压源型PWM整流器的拓扑结构。主电路采用IGBT与二极管反并联的方式。图中，ea、eb和ec为三相对称电源的相电压，va、vb和vc为整流器的交流侧相电压；L和R为电感的等效电感和阻值参数，C为直流滤波电容，RL为直流负载侧的等效阻值参数。

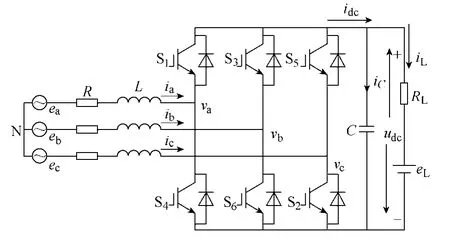
图1 电压型PWM整流器主电路拓扑结构Fig.1 The main circuit topology of voltage type PWM rectifier

经过 3/2坐标变换，其在两相静止坐标系下的数学方程式可表示为

式中，eα、eβ、iα、iβ、vα和vβ分别是αβ 两相静止坐标系下的电源电压、输入电流和整流桥网侧电压。

3 无差拍预测直接功率控制

本文所提无差拍预测直接功率控制方法根据电压源型 PWM整流器的数学方程式，推导出两相静止αβ坐标系下的无差拍预测直接功率控制模型，无需利用电网电压角度信息来进行旋转变换。并由无差拍预测直接功率控制模型计算控制电压矢量在两相静止坐标系下的vα、vβ分量，经SVPWM调制方法调制出开关器件的控制信号，在每一个开关周期都实现对当前周期结束或者下一个周期开始时功率给定值的跟踪控制。

3.1 直接功率控制

DPC控制思想基于瞬时功率理论，由日本学者赤木泰文（H.Akagi）等人在20世纪80年代初期提出，之后得到跟踪研究并被进一步明确化[12,13]。随后波兰学者Mariusz Malinowski提出的基于虚拟磁链定向的直接功率控制（VF-DPC）策略更引起了行业学者对直接功率控制策略广泛关注和研究。瞬时功率理论使得功率、特别是无功功率的定义和计算更加准确，从而使得对瞬时有功功率和瞬时无功功率的控制更加精准。

在αβ两相静止坐标系下，瞬时功率表达式为

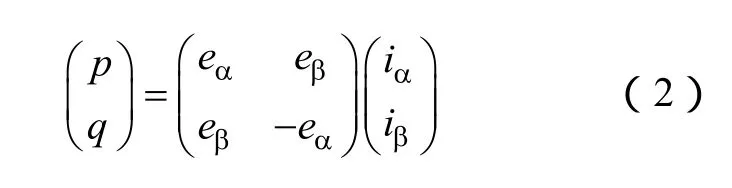
式中，p为电网瞬时有功功率；q为电网瞬时无功功率；eα、eβ为电源电压；iα、iβ为电网电流。

3.2 无差拍预测直接功率控制模型

根据式（1），PWM整流器在t时刻的数学方程表达式如下

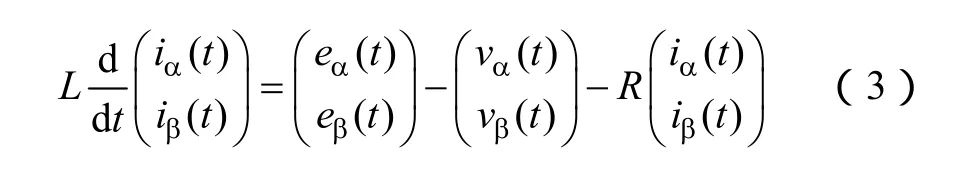
采样周期为Ts时，设kTs时刻交流侧电源电压、整流器交流侧电压以及输入电流分别为e(k)、v(k)、i(k)。为便于分析计算，忽略电阻R带来的影响。并利用正向差分方法对式（3）进行离散化，建立无差拍预测控制模型如下

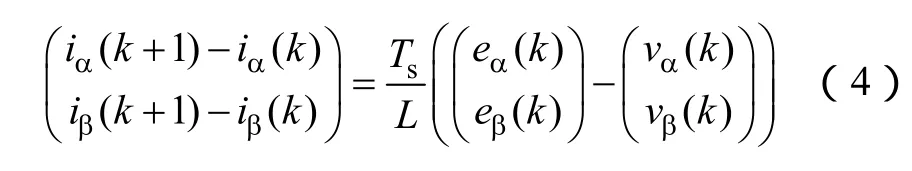
假设采样周期远小于电网电压工频，电源电压大小在相邻两个采样周期可看作不变，即e(k+1)=e(k)。因此，根据式（2）可得连续两个采样周期的瞬时功率改变量为

式中，p(k)、q(k)分别为kTs时刻瞬时有功功率和瞬时无功功率值。

将式（4）代入式（5）中，可得方程式

由于无差拍直接功率控制在每一个开关周期，实现对当前周期结束或者下一个周期开始时功率给定值的跟踪控制，因此，令

并根据方程式（6）推导出控制电压的计算方程式

式中，||eαβ||为电网电压矢量幅值。瞬时无功功率q*(k+1)直接在控制器内给定，有功功率p*(k+1)给定值由整流器直流电压PI控制器输出决定。

3.3 基于内模原理的反馈校正

式（8）给出了无差拍预测直接功率控制的控制方程，当系统工作于稳态时，应有p*(k+1)=p(k)、q*(k+1)=q(k)，从而由式（8）可得

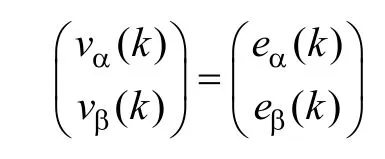
由式（1）推得iα、iβ也均为 0，显然，目标控制电压矢量计算式中瞬时有功功率偏差εp(k)、瞬时无功功率偏差εq(k)输入信息消失后，控制器不能维持输出合适的控制量，也就是说误差值的存在是保证控制器工作所必需的，所以传统的无差拍预测直接功率控制方法存在着稳态误差。

在kTs时刻，采集到实际输出p(k)后，与(k-1)Ts时刻所作的功率预测值p*(k)比较，得到的预测误差为

为了克服预测模型的误差以及控制过程中干扰对系统的影响，在每一步控制作用后，将每一步的预测误差进行叠加，并修正下一步的预测值，进行反馈校正，修正方程式如下

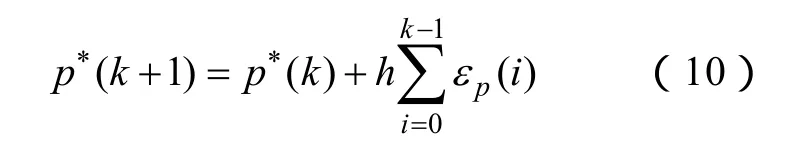
式中，h是加权修正系数。从而

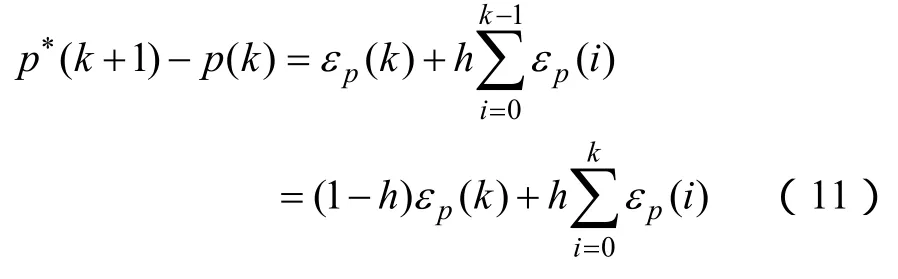
可以看出，修正后的方程也具有数字PI控制器的形式，具有准积分的效果，从而能实现对功率的无静差跟踪，控制器功率预测值的修正方法的等效框图如图2所示。h可以简单取为一个小于0.05的常数[20]。

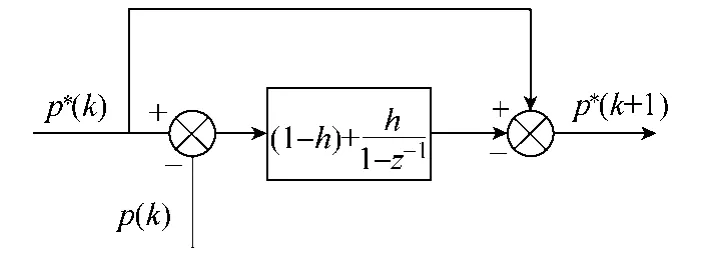
图2 功率预测值修正方法框图Fig.2 Diagram of the power predictive value correction method

在第kTs采样周期，根据重内模理论将(k-1)Ts时刻所作的功率预测值p*(k)加上前k次采样周期预测误差值之和，对预测给定值进行修正，得到对下一个周期功率给定值p*(k+1)的预测，并且一旦预测值与实际采样值之间出现偏差，预测给定值就会做出相应修正，从而使系统做出相应调整。将式（11）代入式（8）中，可得改进后的目标控制电压矢量计算表达式为

并且根据式（11）可以看到，这种反馈校正方法具有准积分效果，可以消除系统的功率静差。控制框图如图3所示。

图3 引入反馈校正的无差拍预测直接功率控制策略框图Fig.3 The frame of deadbeat predictive direct power control strategy with feedback

4 仿真分析和实验验证

使用Matlab/Simulink建立仿真模型，分别对传统无差拍预测直接功率控制策略和加入准积分反馈校正方法的无差拍预测直接功率控制策略进行仿真研究。系统仿真参数完全与实验条件一致，见下表。

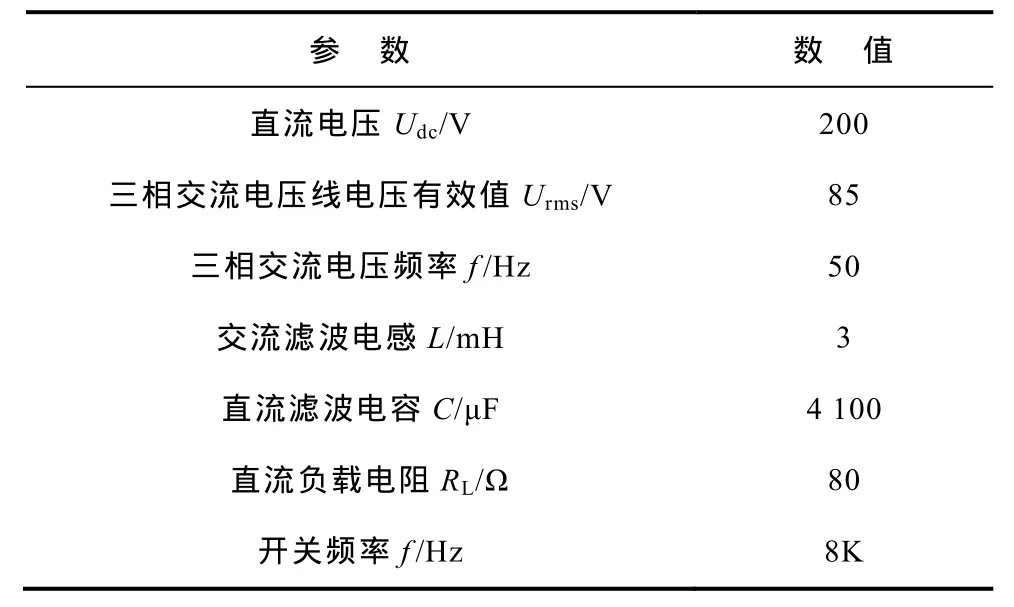
表 系统仿真参数Tab. Parameters of the simulation system

两个仿真模型系统参数相同，在 0.2～0.4s运行在空载状态，在0.4s时，直流侧突加一个80Ω的负载，有功功率突变为500W，无功功率给定为0var，让系统运行在单位功率因数状态下。

为了满足机具行走的效率和安全之间的平衡，临时轨道根据切缝机具的尺寸进行加工，滑轮组小于轨道的宽度4mm，轮组采用齿轮塑料材质（POM）。

传统无差拍预测直接功率控制和加入准积分反馈校正方法的无差拍预测直接功率控制策略的仿真结果如图4和图5所示。因电流值相对于电压值数值较小，为便于分析，将电网a相相电压缩小10倍后与三相电流波形放在同一个图形中进行观测，并分别截取带负载时0.555～0.595s的波形，空载时0.3～0.4s的a相相电压和a相相电流波形，其中空载时a相电流为电流值增大20倍后的波形图。仿真结果图还包括实际有功功率与有功功率给定、实际无功功率与无功功率给定的波形图。

从图4、图5可以看出，采用传统方法与本文所提方法，系统在空载和带负载运行情况下均能稳定运行，从空载运行变换到带负载运行的动态过程响应平稳快速，电流波形呈正弦化。

但图4中显示，传统的无差拍预测直接功率控制实际有功与有功功率给定值始终存在着 26W 左右的静差，实际无功与无功功率给定值在空载时的误差值为4var，0.4s突加负载之后静差也随之变化为-10var。在截取的空载运行时的波形图中，电流超前电压90°，电网吸收无功，与无功波形图吻合。截取的带负载运行情况下的波形图中，放大后可看到电压电流波形过零点没有严格交合，相差角度可以由 tanθ=q/p求得，此时，q=10var，p=500W，θ=arctan0.02=1.145 8°。

图5为采用本文所提方法得到的仿真波形。由图可以看出，有功功率跟踪快速准确，没有静差；无功功率始终只有±2var的波动，平均值为0，在突加负载时波动也很微小。截取的空载运行时的波形图中，电流在零附近均匀波动，平均值为0，无功功率有功功率均为0，这与功率波形图吻合。截取的带负载运行情况下的波形图中，放大后可看到电压电流波形在过零点处严格交合，系统运行在单位功率因数情况下。

图5 引入反馈校正的无差拍预测直接功率控制仿真结果波形Fig.5 Simulation results of deadbeat predictive direct power control with feedback

仿真结果表明，引入积分内模的反馈校正的无差拍直接功率控制方法是有效和正确的。

图6所示为本实验的硬件系统，系统包含了PWM 整流器和直流侧负载电阻。由于实验条件有限，功率波形无法直接测量，本文借助CCS软件，通过D-A转换，再经示波器进行观测。并且只用示波器观测了电网电压单相电压和单相电流波形。

图6 实验硬件系统照片Fig.6 Photo of the experimental system

图7和图8分别为传统的无差拍预测直接功率控制以及本文所提方法的的实验结果波形。包括从空载运行状态突加负载过程的a相电压和电流的动态波形，以及在动态波形图中分别截取的空载、负载时的波形图。

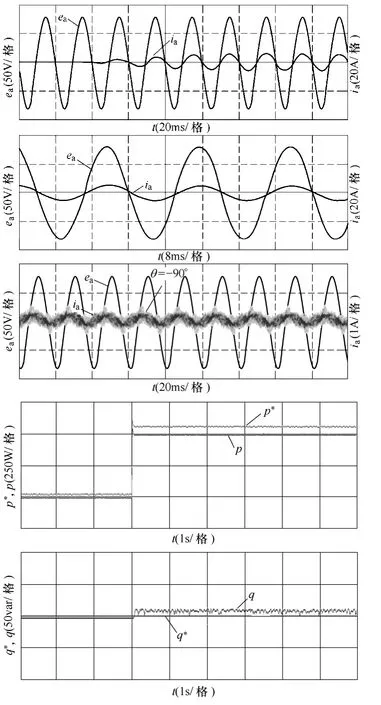
图7 传统无差拍预测直接功率控制实验结果波形图Fig.7 The experimental results waveforms of traditional deadbeat predictive direct power control

图8 引入反馈校正的无差拍预测直接功率控制的实验结果波形图Fig.8 The experimental results waveforms of deadbeat predictive direct power control with feedback

从图中可以看出，传统方法与本文所提控制方法，系统都能运行稳定，动态过程响应快速平稳，电流波形呈现正弦化。

但图7中，空载时，明显看出存在一个峰值为0.1A左右、超前电压波形90°的无功电流；截取的负载运行波形图中，电压电流波形过零点也没有严格交合，这与仿真实验结果吻合。功率波形图中，有功给定与实际有功之间的静差，空载时为30W；带负载时为 58W。无功给定与实际无功之间的静差，空载时为 3.13var；带负载时为 12.5var。实际系统当中，存在着诸如电感大小值，各种杂散损耗影响等参数的误差，造成系统不同运行状态下静差与仿真结果有较小差别。传统控制方法中，存在有功功率、无功功率静差，这个误差值的存在是保证控制器工作所必需的。

图8中，空载时，电流波形在零点附近波动，均值为 0，电压电流波形过零点严格交合。功率波形图中，有功功率响应与给定值重合；无功功率响应始终为给定值0，实现系统的单位功率因数控制。并且，改进后的控制系统，在空载和负载运行状态下均能保持无静差，受系统运行状态与以及参数改变影响小。实验波形表明，加入准积分内模进行前馈补偿的无差拍直接功率控制系统消除了有功和无功功率的静差，有功无功均严格跟踪给定值的大小，实现了功率值的无差跟踪。

5 结论

针对三相电压型 PWM整流器，在无差拍预测直接功率控制的基础上，引入基于内模原理的反馈校正作用机制，提出了一种利用动态过程中的预测误差不断累加来修正下一拍的预测值消除静态误差的控制方法。仿真及实验结果证明了这种无差拍预测直接功率控制方法具有良好的功率动态响应能力，并且功率响应准确无稳态误差，具有一定的应用价值。

[1] 张崇巍,张兴. PWM整流器及其控制[M]. 北京: 机械工业出版社,2012.

[2] Akagi H,Watanabe E H,Aredes M. Instantaneous power theory and applications to power conditioning[M]. Piscataway,NJ: IEEE Press,2007.

[3] Rahmati A,Abrishamifar A. Direct power control of HVDC light system for connecting two network at different frequency[C]. Universities Power Engineering Conference,UPEC 2006,Proceedings of the 41st International,2006,2: 579-583.

[4] 王久和. 电压型PWM整流器的非线性控制[M]. 北京: 机械工业出版社,2008.

[5] Malinowski M. Sensorless control strategies for threephase PWM rectifier[D]. Warsaw,Poland: Inst. Control Ind. Electron. Warsaw University Technology,2001.

[6] Noguchi T,Tomiki H,Kondo S,et al. Direct power control of PWM Converter without power-sorce voltage sensor[J]. IEEE Transactions on Industry Application,1998,34(6): 473-479.

[7] Duarte J L,Van Zwam A,Wijnands C,et al.Reference frames fit for controlling PWM rectifiers[J].IEEE Transactions on Industrial Electronics,1999(46):628-630.

[8] Malinowski M,Kaźmierkowski M P,Hansen S,et al.Virtual flux based direct power control of three-phase PWM rectifier[J]. IEEE Transactions on Ind. Applications,2001,37(4): 1019-1027.

[9] Cortés P,Kazmierkowski M P,Kennel R M,et al.Predictive control in power electronics and drives[J].IEEE Transactions on Industrial Electronics,2008,55(12): 4312-4323.

[10] Vazquez S,Sanchez J A,Carrasco J M,et al. Modelbased direct power control for three-phase power converters[J]. IEEE Transactions on Industrial Electronics,2008,55(4): 1647-1657.

[11] 李玉玲,鲍建宇,张仲超. 基于模型预测控制的单位功率因数电流型 PWM 整流器[J]. 中国电机工程学报,2006,26(19): 60-64.

Li Yuling,Bao Jianyu,Zhang Zhongchao. Unity power factor current source pwm rectifier based on model predictive control[J]. Proceedings of the CSEE,2006,26(19): 60-64.

[12] 杨勇,赵方平,阮毅,等. 三相并网逆变器模型电流预测控制技术[J]. 电工技术学报,2011,26(6):153-159.

Yang Yong,Zhao Fangping,Ruan Yi,et al. Model current predictive control for three-phase grid-connected inverters[J]. Transactions of China Electrotechnical Society,2011,26(6): 153-159.

[13] 尚磊,孙丹,胡家兵,等. 三相电压型并网逆变器预测直接功率控制[J]. 电工技术学报,2011,26(7):216-222.

Shang Lei,Sun Dan,Hu Jiabing,et al. Predictive direct power control of three-phase grid-connected voltage-sourced inverters[J]. Transactions of China Electrotechnical Society,2011,26(7): 216-222.

[14] 杨兴武,姜建国. 电压型 PWM 整流器预测直接功率控制[J]. 中国电机工程学报,2011,31(3): 34-39.

Yang Xingwu,Jiang Jianguo. Predictive direct power control for three-phase voltage source PWM rectifiers[J]. Proceedings of the CSEE,2011,31(3): 34-39.

[15] 杨勇,阮毅,叶斌英,等. 三相并网逆变器无差拍电流预测控制方法[J]. 中国电机工程学报,2009,29(33): 40-46.

Yang Yong,Ruan Yi,Ye Binying,et al. Deadbeat predictive current control method for three-phase gridconnected inverters[J]. Proceedings of the CSEE,2009,29(33): 40-46.

[16] Bouafia A,Gaubert J P,Krim F. Predictive direct power control of three-phase pulse width modulation(PWM)rectifier using space-vector modulation(SVM)[J]. IEEE Transactions on Power Electronics,2010,25(1): 228-236.

[17] 王万良. 现代控制工程[M]. 北京: 高等教育出版社,2011.

[18] 唐欣,罗安,涂春鸣. 基于递推积分 PI的混合型有源电力滤波器电流控制[J]. 中国电机工程学报,2003,23(10): 38-41.

Tang Xin,Luo An,Tu Chunming. Recursive integral PI for current control of hybrid active power filter[J].Proceedings of the CSEE,2003,23(10): 38-41.

[19] Ying-Yu Tzou,Rong-Shyang Ou,Shih-Liang Jung,et al. High-performance programmable AC power source with low harmonic distortion using DSP-based repetitive control technique[J]. IEEE Transactions on Power Electronics,1997,12(4): 715-725.

[20] 张凯. 基于重复控制原理的 CVCF-PWM 逆变器波形控制技术研究[D]. 武汉: 华中科技大学,2000.

[21] Francis B A,Wonham W M. The internal model principle for linear multivariable regulators[J]. Appl.Math. Opt.,1975,2(2): 170-194.