一种基于加速度预估计的机动目标跟踪算法

宋振宇，张翔宇，张　磊（海军航空工程学院.科研部；.电子与信息工程系；.接改装训练大队，山东烟台264001）



一种基于加速度预估计的机动目标跟踪算法

宋振宇a，张翔宇b，张磊c
（海军航空工程学院a.科研部；b.电子与信息工程系；c.接改装训练大队，山东烟台264001）

摘要：研究分析了几种典型单机动目标模型的建模方法，针对现有单机动目标模型中机动参数需要先验假设，并且不能随目标机动情况的改变而自适应调整的问题，提出了一种加速度预估计模型（Acceleration Pre-estimation Model，APM）。该模型首先用位置量测对机动加速度进行预估计；然后，将加速度估计值作为系统的输入控制项建模；将估计误差看做系统的机动控制项，并作为系统的相关噪声建模。由于APM模型中，加速度机动参数是通过位置量测实时估计得到的，不需要先验假设。与现有单机动目标模型相比，该模型的自适应能力得到了提高。

关键词：机动目标；跟踪算法；加速度估计；自适应

目标模型是目标跟踪算法的基础，它与目标运动的匹配程度更是决定了滤波算法的跟踪效果[1]。对于机动目标，由于其机动特性往往是由加速度变化引起的，因而对机动目标建模的核心就是要对机动加速度建模。将目标的机动加速度描述为时间相关的随机过程，是目前大多数文献采用的建模方法[2]。其中，较为典型的是Singer[3]、CS[4]和Jerk[5]3种模型。虽然以上3种模型通过对加速度或加加速度进行色噪声建模[6]，实现了对该随机过程较为准确的描述，但是由于模型的建立过程需要对目标未知的加速度机动参数进行合理的先验假设[7]，这就限制了3种模型的适用性。为此，本文提出了一种加速度预估计模型（Acceleration Pre-estimation Model，APM）。该模型首先用相邻几个采样时刻的位置量测对机动加速度预估计；然后，将加速度估计值作为系统的输入控制项建模；将估计误差看作系统的机动控制项[8]，并作为系统的相关噪声（色噪声）建模。该模型建模过程中，机动参数是由位置量测实时估计得到的，与Singer、CS和Jerk模型相比，不需要假设机动参数就能够匹配不同机动运动环境，具有较高的自适应能力。

1　APM模型

APM模型的建模主要分为3步。第1步，通过对机动运动线性化处理，用位置量测值对加速度进行预估计。第2步，将加速度估计误差看作系统的机动控制项，并作为系统的相关噪声（色噪声）建模。第3步，通过机动控制项的相关噪声模型，推导出APM模型。

1.1机动加速度的预估计

对于机动运动目标，虽然其加速度在不断变化，但是在采样率[9-10]足够高的前提下，可以将相邻N个采样间隔间的变加速运动线性化为匀加速运动，一般来说N越大，线性化误差越大。

如图1所示，设采样周期为T，将一目标从t-T时刻到t+2T时刻的机动运动线性化为加速度为a(t)的匀加速直线运动，用(t+iT)、v(t+iT)分别表示t+iT时刻目标的位置和速度。

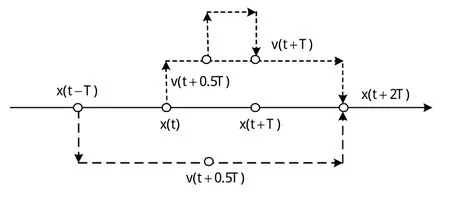
图1　机动加速度的线性化表示Fig.1 Linear representaion of the maneuver acceleration

由匀加速直线运动的性质可得：

由式（1）、（2）得

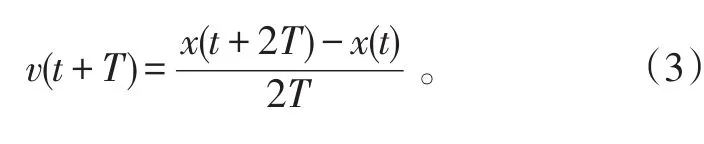
同理可得

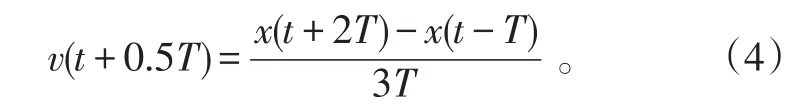
由式（3）、（4）可得

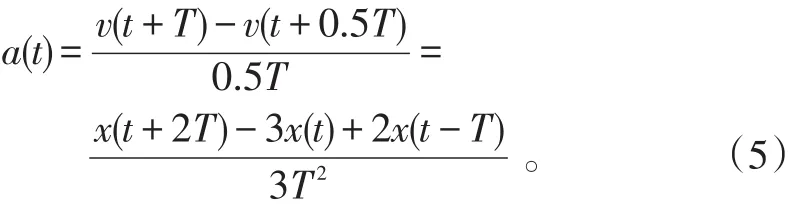
在雷达跟踪系统中，由于极坐标系下位置量测值（径向距离和方位角）可以转换为直角坐标系各坐标轴方向的位置量测值，因而可以通过式（5）用位置量测值对机动加速度a(t)进行预估计。

设Z(t+iT)为t+iT采样时刻轴的位置量测值，且假定量测噪声为零均值高斯白噪声，并用Q(t+iT)表示对应时刻的噪声方差。将Z(t+iT)代入式（5）得到t时刻加速度估计值为式（6）中：Za(t)表示加速度估计值；(t)表示估计误差，且服从零均值方差为Qa(t)的高斯分布。

Qa(t)可由各时刻量测噪声方差表示为

由式（6）可以看出，采用该式对目标跟踪有2个周期的延迟，且t、t-T和t+2T时刻是相关的，因而直接采用其进行kalman滤波是一种近似。由式（7）可以看出，机动加速度a(t)由估计值Za(t)和估计误差(t)组成。其中，Za(t)是由位置量测值估计得到的，而(t)是一个随机噪声。因此，在机动目标建模过程中，可以将加速度估计值作为系统的输入控制项建模；将估计误差看作系统的机动控制项，并作为系统的相关噪声建模。

1.2机动控制项的建模

文献[1]指出将机动控制项按照自相关色噪声建模，相比按照白噪声建模更切合实际，而且由式（6）、（7）可以看出，各个时刻的加速度估计误差(t)显然都是相关的。为此，将机动控制项（加速度估计误差）(t)按照自相关的零均值随机过程建模为式（8）中：α为相关系数；Qa(t)为机动控制项（加速度估计误差）方差，可由式（7）中的Qa(t)确定。

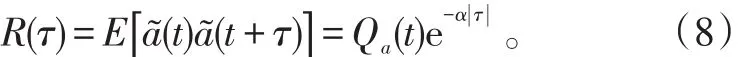
对时间相关函数R(τ)应用Wiener-Kolmogorov白化程序后，机动控制项可用输入为白噪声的一阶时间相关模型来表征，即式中，ω(t)是均值为0、方差为2αQa(t)的高斯白噪声。

1.3 APM模型描述

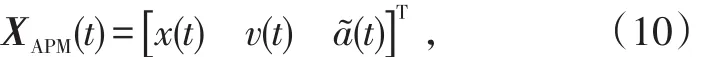
由式（6）、（9）得系统的状态方程为：式（11）中：Za(t)表示系统的输入控制项；ωAPM(t)表示系统的过程噪声；a(t)表示系统的机动加速度；状态转移矩阵

；过程噪声分布矩阵BAPM=[ ]

0 0 1T；输入控制矩阵CAPM=[ ]

0 1 0T。将式（9）代入式（11）有：

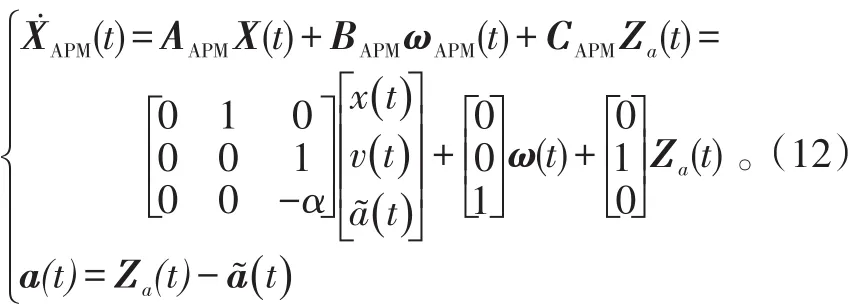
式（12）为APM模型的连续时间表达式。其中，输入控制项Za(t)由加速度的估计值确定；系统的过程噪声ω(t)由加速度的估计误差确定。因此，APM模型不需要对机动参数进行先验假设。

设采样周期为T，通过文献[1]提出的离散化方法，对式（12）进行离散化处理得到离散状态方程为：

式（13）中：状态转移矩阵

输入控制矩阵

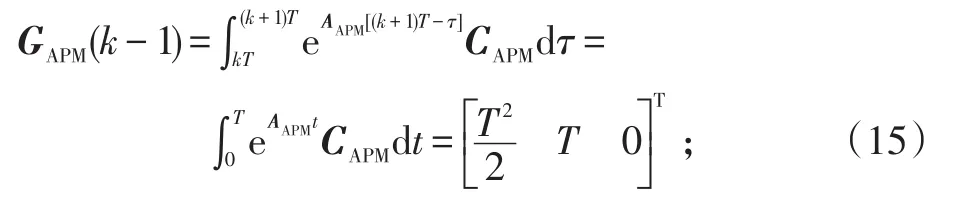
过程噪声WAPM(k-1)协方差

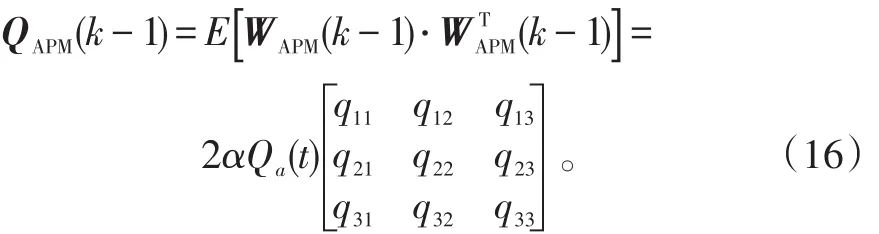
式（16）中：

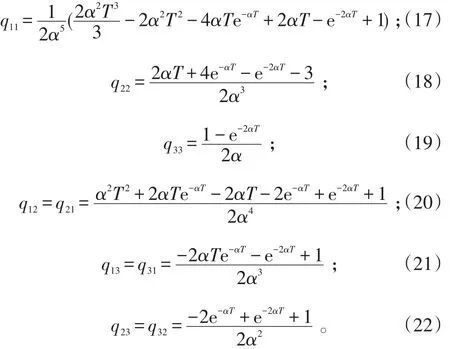
1.4 APM模型量测方程的建立

由上述分析可知，目标跟踪在直角坐标系下进行，而k时刻的雷达量测[]ρ(k)θ(k)ε(k)却在极坐标系下获得。这时，采用无偏转换的方法将目标量测转换到直角坐标系，则直角坐标系下的目标量测可对应表示为：

式（23）中：

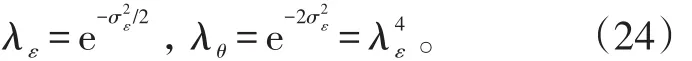
因此，量测方程可表示为式（25）中：Z(k )为无偏转换后的量测数据；(k )为状态向量；H(k ) =[1 0 0 0]为量测矩阵；W(k )为零均值、恒定方差的附加高斯白噪声序列。

2　基于APM模型的机动目标跟踪算法

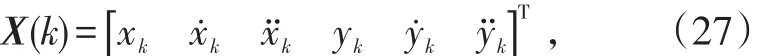
输入控制矩阵

过程噪声协方差

2）加速度预估计。从对APM模型的建模过程可以看出，APM-UCMKF算法首先要通过位置量测值对加速度进行预估计；然后，用卡尔曼滤波算法进行跟踪滤波。设加速度估计值为Za(k-1)，估计误差方差为Qa(k-1)，则由式（6）、（7）可知Za(k-1)为：式（32）中：Z(k+1)、Z(k-1)、Z(k-2)和Z(k+1)、Z(k-1)和Z(k-2)分别表示k+1、k-1和k-2时刻方向和方位置量测值。

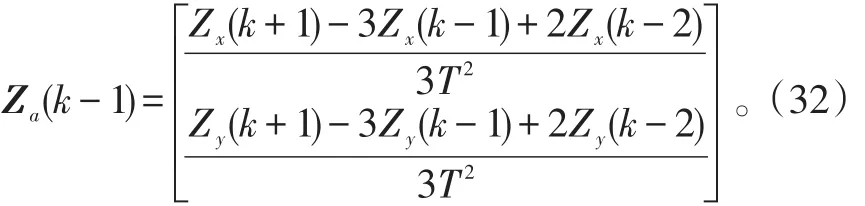
Qa(k-1)表示为：式（33）中：Q(k+1)、Q(k-1)、Q(k-2)和Q(k+1)、Q(k-1)和Q(k-2)分别表示k+1、k-1和k-2时刻方向和方向位置量测值量测误差的方差。

3）滤波。

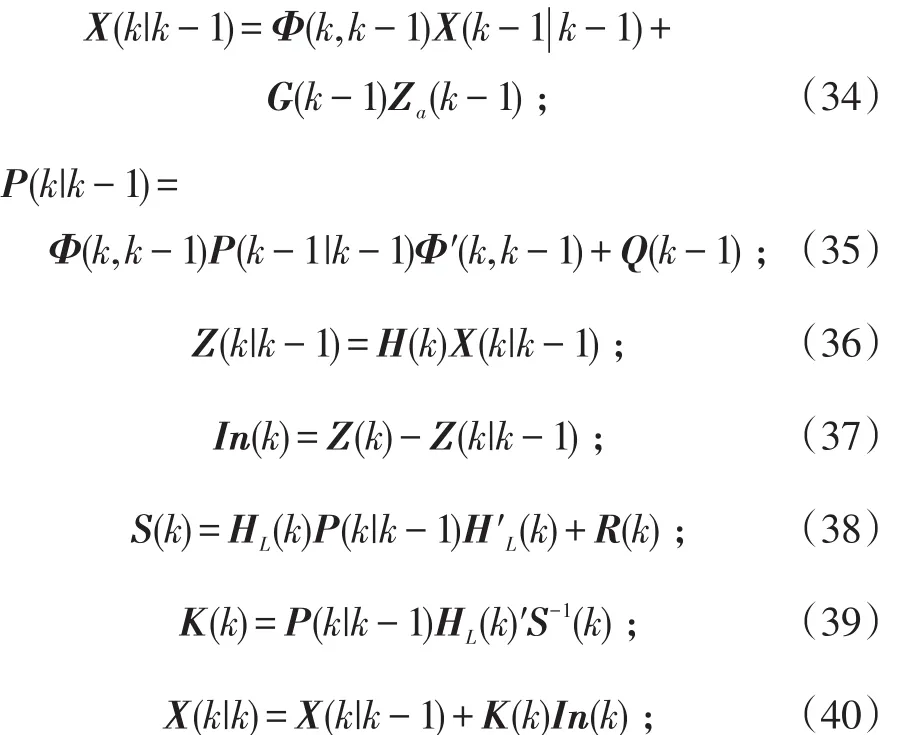
3　仿真分析与结论

3.1场景设置

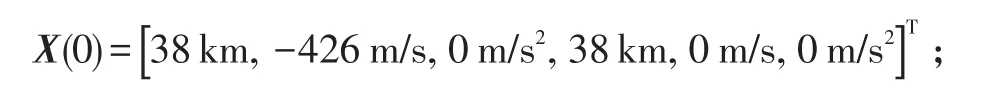
目标起始时刻状态：目标运动过程历时90 s；目标直角坐标系下运动轨迹发生机动时刻及加速度大小见图2。

仿真过程中，假设雷达采样周期为T=1 s，距离量测误差标准差σr=100 m，方位角量测误差标准差σφ=0.3°。各算法采用2点差分法进行初始化，评价指标为方向和方向位置、速度和加速度的均方根（RMS）误差。

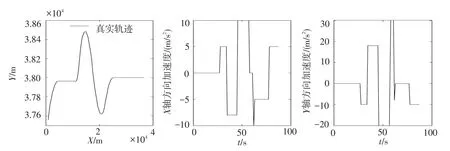
图2　目标运动轨迹Fig.2 Trajectorof target

仿真具体包括弱机动和强机动2种情况。

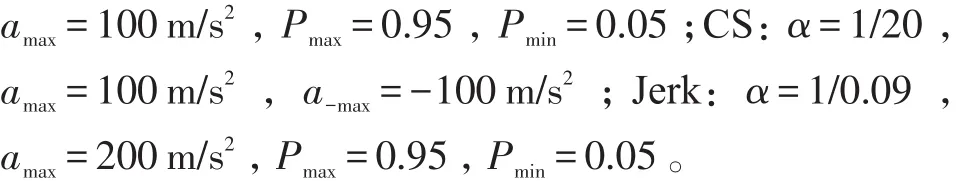
3.2仿真结果

1）弱机动情况。图3为目标弱机动情况4类模型算法仿真效果比较图，从图3中可以看出，本仿真条件下Singer、CS和Jerk算法的精度越来越高，本章提出的APM算法，其位置跟踪精度略优于Jerk算法。

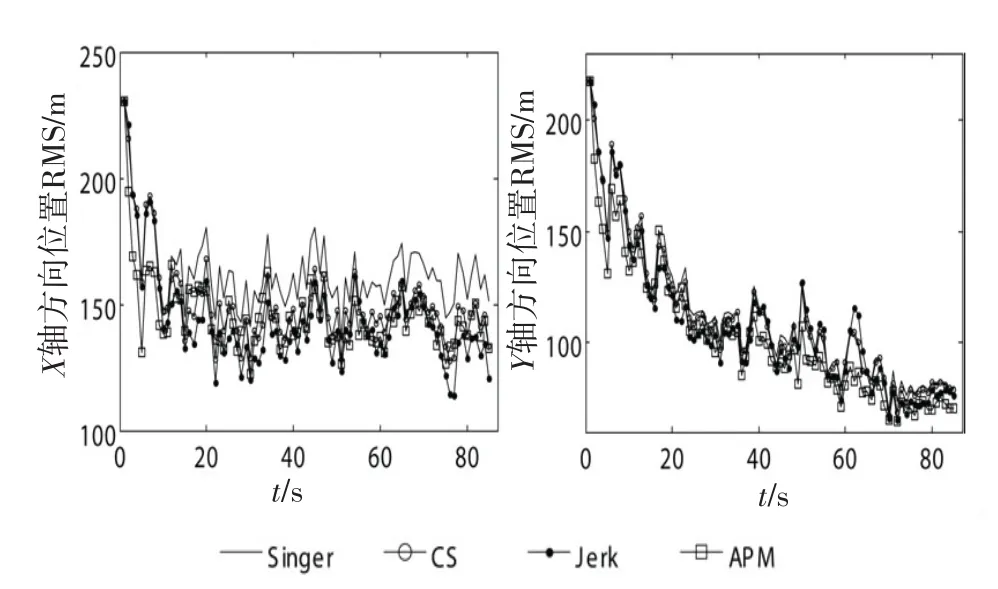
图3　各类算法跟踪精度比较Fig.3 RMS of algorithms

2）强机动情况。Singer、CS和Jerk参数未改变，依旧为弱机动参数时的仿真结果，如图4所示。从图4中可以看出，本仿真条件下Singer、CS和Jerk算法的精度受机动环境改变的影响较大，RMS曲线不稳定。所以Singer、CS和Jerk模型只有在机动参数假设合理时，才能与机动环境匹配，跟踪效果才会好，其适应性较差。

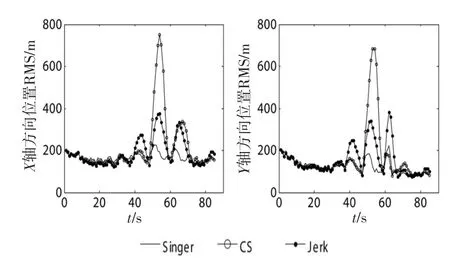
图4　各类算法跟踪精度比较Fig.4 RMS of algorithms

图5为目标强机动情况Singer、CS和Jerk模型参数改变后与APM算法的跟踪效果比较图。从图5中可看出，APM算法位置跟踪精度略优于Jerk算法，且相对于其他3种算法更为稳定。这是由于目标机动情况发生改变，Singer、CS和Jerk算法中由于描述机动运动的先验参数需要调整，但对APM算法，其参数却不需调整，这也是APM算法相比以上3种算法的优势。

图5　各类算法跟踪精度比较Fig.5 RMS of algorithms

4　结论

本文主要研究了加速度预估计模型（Acceleration Pre-estimation Model，APM）及其目标跟踪算法。对机动运动的自适应能力方面，与现有Singer、CS和Jerk模型相比，APM模型中机动参数可以由位置量测估计。因此，不需要先验假设机动参数就可以匹配不同环境的机动运动，具有较强的自适应能力。在跟踪精度方面，基于APM模型的跟踪算法的跟踪精度略优于Jerk模型，且具有较高的自适应能力。

参考文献：

[1]何友，修建娟，张晶炜，等.雷达数据处理及应用[M]. 2 版.北京：电子工业出版社，2009：148-155. HEOU，IU JIANJUAN，ZHANG JINGWEI，et al. Radar data processing with applications[M]. 2nd ed. Beijing：Publishing House of Electronics Industr，2009：148-155.（in Chinese）

[2]高羽，张建秋，尹建君.机动目标的多项式预测及其跟踪算法[J].航空学报，2009，14（8）：326-331. GAOU，ZHANG JIANQIU，IN JIANJUN. Polnomial prediction and tracking of maneuvering target[J]. Acta Aeronautica et Astronautica Sinica，2009，14（8）：326-331.（in Chinese）

[3]党建武，黄建国.机动目标自适应高斯模型与跟踪算法[J].电讯技术，2003（2）：109-113. DANG JIANWU，HUANG JIANGUO. Adaptive Gauss model and tracking algorithm of maneuvering target[J]. Telecommunication Engineering，2003（2）：109-113.（in Chinese）

[4]李涛，王宝树，乔向东.基于截断正态概率模型的改进目标跟踪算法[J].系统工程与电子技术，2003，25（10）：1289-1291. LI TAO，WANG BAOSHU，QIAOIANGDONG.An improved target tracking algorithm based on truncation gauss probabilitmodel[J]. Journal of Engineering and Electronics，2003，25（10）：1289-1291.（in Chinese）

[5]WANG WEI，HOU HONGLU. An improved current satatistical model for maneuvering target tracking[C]//IEEE Conference on Industrial Electronics and Applications. 2009：212-235.

[6]WU JIANFENG，LI GAO，MA FUZHOU. Research on target tracking algorithm using improved current statistical model[C]//Proceedings of International Conference on Electronics and Control Engineering. 2011：2517-2515.

[7]刁联旺，杨静宇.一种改进的机动目标的当前统计模型的描述[J].兵工学报，2002，26（6）：824-828. DIAO LIANWANG，ANG JINGU. An improved description of current statistical model for maneuvering taget[J]. Acta Armamentarii，2002，26（6）：824-828.（in Chinese）

[8]罗笑冰，王宏强，黎湘，等.机动目标α-Jerk模型[J].信号处理，2007，23（4）：481-484. LUOIAOBING，WANG HONGQIANG，LIIANG，et al. A α-Jerk model for tracking maneuvering targets[J]. Signal Processing，2007，23（4）：481-484.（in Chinese）

[9]候俊林，张丽珂，朱越.基于CS-Jerk模型的改进机动目标跟踪算法[J].弹箭与制导学报，2012，34（6）：125-128. HOU JUNLIN，ZHANG LIKE，ZHUUE. Modified maneuvering target tracking algorithm based on CS- Jerk model[J]. Journal of Projectiles，Rockets，Missiles and Guidance，2012，34（6）：125-128.（in Chinese）

[10]张磊，胡善春，贾舒宜.一种带径向速度量测的Jerk-EKF机动目标跟踪算法[J].空军预警学院学报，2013，27 （4）：267-269. ZHANG LEI，HU SHANCHUN，JIA SHUI. Algorithm for Jerk-EKF maneuvering target tracking with radial velocitmeasurement[J]. Journal of Air Force EarlWarning Academ，2013，27（4）：267-269.（in Chinese）

Algorithm for Maneuvering Target Trackingg with Acceleration Pre-estimatiioonn

Abstrraacctt:: Some kinds of tpical maneuvering model were analzed. Due to the problem of un-adaptive adjustment of target model, which needed a priori hpothesis with the change of target maneuver condition, a novel acceleration pre-estimation model was proposed. Firstl, the pre-estimation of acceleration was gained bposition measurements. Then, the accelera⁃tion estimate was modeled as control input. At last, the estimate error was regarded as the maneuvering control input and modeled as the correlative noise of sstem. In the proposed model, acceleration maneuvering parameter was estimated breal-time position measurements and the self-adjusting performance was improved comparing with the eisting models.

作者简介：宋振宇（1961-），男，副教授，硕士。

基金项目：国家自然科学基金资助项目（61372027，61102165）

收稿日期：2014-10-28；

DOI:10.7682/j.issn.1673-1522.2015.02.001

文章编号：1673-1522（2015）02-0101-05

文献标志码：A

中图分类号：TN958.93

修回日期：2015-01-04