基于兰彻斯特方程的防御作战效能分析

丛红日，吴福初，陈邓安（海军航空工程学院指挥系，山东烟台264001）



基于兰彻斯特方程的防御作战效能分析

丛红日，吴福初，陈邓安
（海军航空工程学院指挥系，山东烟台264001）

摘要：对防御作战的重要意义、目的和基本方法进行了分析总结，在此基础上，通过对兰彻斯特方程的毁伤系数进行分解和细化，建立了体现防御的兰彻斯特方程，给出了具体算例，并简要分析了其对平局条件、交战强度等方面的影响。

关键词：兰彻斯特方程；防御作战；作战模型；效能分析；毁伤系数；防御系数

防御作战简称防御，是指抗击敌方进攻的作战，包括战略、战役和战术范围的防御，是作战的基本类型之一[1]。防御作战的主要目的与作战效果是保存自己，消耗敌人。防御作战包括3种基本方法：防止被发现并定位、机动防御和防止被毁伤。

由于防御是相对进攻而言的，防御的效果主要体现为对进攻效果的削弱程度，而且与进攻相比，专门用于防御的武器装备相对较少，防御主要体现为作战方法的有效运用，而武器装备的使用在其中居于次要地位。因此，对防御作战进行定量分析非常困难。

但在作战过程中，防御作战与进攻作战同样重要。要想对作战问题进行定量分析研究，离开对防御作战的定量分析研究不但是不全面、不完整的，而且在某种意义上来讲，也是不可能的。因此，必须通过研究，找到一种对防御作战进行定量分析研究的适当方法。本文以兰彻斯特方程为基础，提出一种对防御作战进行定量分析研究的思路和方法。

1　兰彻斯特方程及其重要意义

1.1兰彻斯特方程的重要意义

1916年，英国人Lanchester提出了兰彻斯特方程。该方程在作战模型、作战仿真、军事运筹等领域得到了广泛应用，成为了一种重要的基础性工具[2]。

作战是一种典型的对抗性的、此消彼长的动态过程[3-4]，而兰彻斯特方程以微分方程的形式描述作战过程，正确反映了作战过程的本质。因此，尽管兰彻斯特方程存在一些问题和不足，但仍然是以数学方法描述作战过程的最好方法之一[5]。尤其是如何在兰彻斯特方程中体现防御，是一个非常有意义的研究课题。

1.2经典兰彻斯特方程

经典的单兵种兰彻斯特方程为[2]：式（1）中：A、B分别是交战甲、乙双方的兵力数量；a、b分别是甲、乙双方的毁伤系数。

多兵种兰彻斯特方程为[2]：式（2）中：A、B分别是交战甲、乙双方的兵力向量；ΦA、ΦB均是非负矩阵，分别称为交战甲、乙双方对对方的毁伤系数矩阵；ΨA、ΨB均是列和不超过1的非负矩阵，分别称为交战甲、乙双方的火力分配矩阵；“*”算子为矩阵对应元素相乘。

1.3兰彻斯特方程的缺陷

经过长期的研究和应用，兰彻斯特方程的缺陷逐渐暴露出来。由于应用的背景和场合不同，兰彻斯特方程的缺陷或局限性表现各不相同[6]。但从基本方面来讲，无论是单兵种兰彻斯特方程，还是多兵种兰彻斯特方程，兰彻斯特方程都是以毁伤系数来统一表示交战双方的作战能力，过于简单，也过于笼统，难以反映作战影响因素的多样性，也难以反映作战过程的复杂性[7]。

其中，在兰彻斯特方程中，虽然毁伤系数中也蕴含了防御能力，但没有显式地表现出来，没有正确反映防御在作战中的重要地位。

2　体现防御的兰彻斯特方程

2.1防御作战能力的表示

从本质上讲，防御作战的效果最终都体现为降低敌方的毁伤效果。因此，防御作战的作战能力可用防御系数来表示，防御系数越大，对敌方以毁伤系数表示的毁伤能力的降低幅度越大，防御能力也就越强。

防御系数是实际作战过程中防御能力（不包括抗击能力）的综合表示。影响防御系数大小的主要因素包括：指挥员的指挥水平、武器装备水平、人员素质与训练水平、战场环境等，这其中既有客观因素，如武器装备水平、战场环境等，又有主观因素，如指挥员的指挥等；既有相对确定性的因素，如武器装备水平等，又有偶然性因素，如战场环境等。因此，防御系数本质上是一个变量。例如，同样一支部队，由不同的指挥员进行指挥，或者在不同的作战环境中作战，其防御能力可能会存在很大差异。但对于一次具体的作战来讲，虽然在作战过程中防御能力也会发生变化，但通常变化不会太大，因此，可以近似地看做一个常量。至于防御系数的具体取值，则需要综合分析对防御能力产生影响的各种因素，通过一定的评估方法（如层次分析法、专家评估法等）来获得。

2.2体现防御的兰彻斯特方程的一般形式

通过把防御系数引入兰彻斯特方程，就可以在兰彻斯特方程中显式地体现防御作战，通过把攻击（体现为毁伤系数）和防御（体现为防御系数）进行区分，把防御的效果明确体现出来，从而有利于对作战过程进行更精确的描述和研究。

具体方法是把传统的兰彻斯特方程中的毁伤系数进行分解、细化。为此，首先需要引入2个新概念。

定义1：基本防御条件。这是指只进行火力抗击而不采取其他防御措施的防御条件。

定义2：理论毁伤系数。这是交战双方在基本防御条件下的毁伤系数。

由于防御的效果体现为削弱、降低敌方的毁伤效果。因此，式（3）中：DA、DB分别为交战双方的防御系数矩阵；ΦA0、ΦB0分别为交战双方的理论毁伤系数矩阵；“/”算子表示矩阵对应元素相除。

基本防御条件只是为了研究问题的方便而规定的一种特殊条件。在一些比较简单的作战中，如冷兵器时代的格斗、现代作战中短兵相接的战斗、对攻战中的战斗等，较符合基本防御条件。但是，在实际作战中通常很难满足基本防御条件，并不能否定规定的基本防御条件的合理性。

由定义可知，在基本防御条件下，DA=1，DB=1，即矩阵中各元素均为1，而在作战中，交战双方通常都会采取各种防御措施，因此，DA≥1，DB≥1，即矩阵中各元素均大于等于1。也就是说，通过防御，能降低敌方的的毁伤能力，减小毁伤系数。

把上式代入多兵种兰彻斯特方程，则：

ì

ïd

ídtB0ABB，（4）

îdtA0BAA式中，“*”、“/”定义同前。

这就是体现防御的多兵种兰彻斯特方程，也是体现防御的兰彻斯特方程的一般形式。

2.3毁伤系数与防御能力系数的确定

在利用兰彻斯特方程解决作战问题的过程中，如何评估和确定毁伤系数是一个非常困难的问题，因为虽然己方的攻击能力可以通过一定的方法来确定[8]，但敌方的防御能力对毁伤系数也有重要影响。相反，如果把毁伤系数进行分解，在规定的基本防御条件下，理论毁伤系数主要反映交战双方的攻击能力，可以采取一定方法相对精确地进行评估[9]，而且所确定出的毁伤系数的含义也更加明确，更有利于利用兰彻斯特方程来研究作战问题。

至于防御能力系数DA、DB，则主要是对敌方防御能力的评估。虽然也很困难，但由于需要考虑的因素及其之间的相互关系已大大简化，相对就比较简单。至于如何来确定防御能力系数DA、DB，已经超出了本文的研究范围，就不作更深入的研究和讨论。

2.4算例

1）基本想定。为了简化问题，这里以交战双方均为单兵种的情况为例进行分析。事实上，多兵种交战的情况只是更加复杂，需要采用矩阵形式进行表示和计算，并无本质区别。

设：交战甲、乙双方的初始兵力数量分别为1 000个作战单位和800个作战单位，即

设：交战甲、乙双方的理论毁伤系数均为1，即在基本防御条件下，交战双方的每个作战单位在单位时间内均能毁伤对方的1个作战单位，即

至于防御能力，为了比较，设定2种典型情况。

情况1：交战甲、乙双方均只进行火力抗击，不采取其他防御措施，即满足基本防御条件，此时，根据定义，则

情况2：交战甲、乙双方的防御能力系数分别为1 和4，即

以上想定情况经整理后见表1。

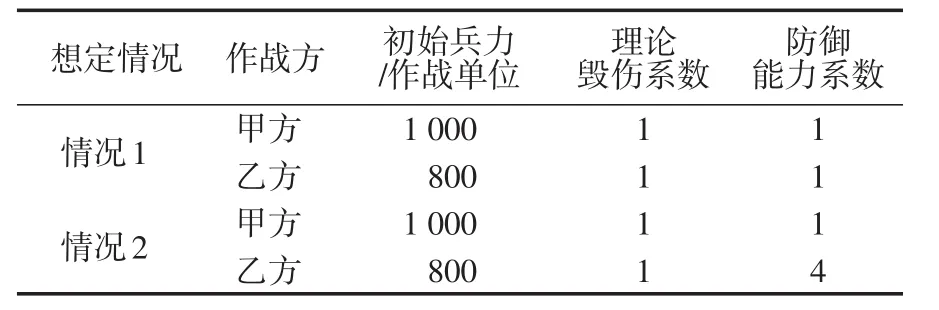
表1　交战情况想定Tab.1 Scenarios of operating instance

2）计算。把情况1的各个参数带入式（4）进行求解，则当作战至约2.2个单位时间时，乙方所有作战单位均被消灭，而此时，甲方还剩下600个作战单位的兵力，甲方获胜。把情况2的各个参数带入式（4）进行求解，则当作战至约2.95个单位时间时，甲方所有作战单位均被消灭，而此时，乙方还剩下约624个作战单位的兵力，乙方获胜。计算结果经整理后见表2。

表2　计算结果Tab.2 Calculation results

3）计算结果分析。计算结果表明，在其他情况完全相同的情况下，防御能力对交战结果能产生决定性影响。在情况1时，由于交战双方的理论毁伤能力和防御能力均相同，甲方由于兵力数量的优势而获胜；而在情况2时，乙方通过提高防御能力有效降低了对方对己方的实际毁伤能力，并最终取得了胜利。

本算例还说明，实力相对较弱的一方（通常为防御方，在本例中为乙方），只要能够有效组织防御（防御的形式可以多种多样，如阵地防御、机动防御等），就有可能战胜对手，从而以弱胜强，古今中外战争史中的大量战例都充分证明了这一点。当然，如何有效组织防御，这是对防御方防御能力（特别是指挥员的指挥能力）的极大考验。

3　补充分析

3.1平局条件分析

对平局条件进行研究和讨论是利用兰彻斯特方程研究作战问题的一种重要方法。当交战双方战成平局时，反映了交战双方的实际作战能力相当[2]。也就是说，可以通过对平局条件的研究来从总体上对交战双方的实际作战能力进行研究。

针对单兵种兰彻斯特方程的平局条件为[2]

如果采用体现防御的多兵种兰彻斯特方程的形式，并使用相应参数的小写来表示一个兵种的情况，则平局条件为

即

从上式就可以清楚地看出，以理论毁伤系数表示的攻击能力和以防御系数表示的防御能力对作战能力起着同等重要的作用，这从理论上证明了进攻与防御同样重要。

3.2对交战强度的影响

在多兵种作战中，如何进行最优火力（兵力）分配是一个重要的战术问题[10]。在文献[2]中，沙基昌通过分析给出了一个最优策略，即：交战双方都应选择交战强度最大的对手作为首选作战对象。

交战强度是指交战时我对敌毁伤系数与敌对我毁伤系数乘积的几何平均值。

使用相应参数的小写来表示多兵种交战中一个兵种的情况，用j表示交战强度，则

显然，交战双方以防御系数表示的防御能力和以理论毁伤系数表示的攻击能力对交战强度具有同等重要的影响。防御能力越低，则交战强度越大。因此，根据最优策略，在其他条件相同或相当的情况下，应选择防御能力较低的对手作为首选作战对象。

4　结语

本文对防御作战的基本方法和作战效果进行了分析总结，在此基础上，通过对兰彻斯特方程的毁伤系数进行分解和细化，建立了体现防御的兰彻斯特方程，并进行了简要分析，为使用兰彻斯特方程研究作战问题提出了一种新的思路和方法，但对于如何确定防御系数等问题没有深入进行探讨，有待在以后的研究中加以完善。

参考文献：

[1]全军军事术语管理委员会.中国人民解放军军语[M].北京：军事科学出版社，2011：77-77. THE PLA MILITARTERMINOLOGMANAGEMENG COMMITTEE. Militarterms of the chinese people’s liberation arm[M]. Beijing：MilitarScience Publishing Compan，2011：77-77.（in Chinese）

[2]沙基昌.数理战术学[M].北京：科学出版社，2003：6-64. SHA JICHANG. Mathematical tactics[M]. Beijing：Science Press，2003：6-64.（in Chinese）

[3]王勇，孙涛，李小偎，等.基于Lanchester方程的作战过程建模及仿真研究[J].系统工程与电子技术，2009，31 （7）：1677-1679. WANGONG，SUN TAO，LIIAOWEI，et al. Modeling and simulation of combating process based on Lanchester equation[J]. Sstems Engineering and Electronics，2009，31（7）：1677-1679.（in Chinese）

[4]巨金川.兰切斯特方程的推广及其作战应用[J].电光与控制，2009，16（10）：22-25. JU JINCHUAN. Improvement of Lanchester equation and its application in combat[J]. Electronics Optics & Control，2009，16（10）：22-25.（in Chinese）

[5]张佳琳，赵琳. MWGM：基于兰彻斯特方程的微观兵棋推演模型[J].计算机工程与设计，2011，32（11）：3807-3810. ZHANG JIALIN，ZHAO LIN. MWGM：microcosmic war game model based on Lanchester equation[J]. Computer Engineering and Design，2011，32（11）：3807-3810.（in Chinese）

[6]朱刚，谭贤四，王红.体系对抗中信息与人和武器关系的SD模型[J].装备学院学报，2014，25（4）：133-137 ZHU GANG，TANIANSI，WANG HONG. SD model of information，human and weapons relationship in the sstem of sstems combat[J]. Journal of Equipment Academ，2014，25（4）：133-137.（in Chinese）

[7]车进喜，李钟敏，高博，等.联合作战中光电对抗系统作战效能评估[J].光学与光电技术，2013，11（5）：52-55 CHE JINI，LI ZHONGMIN，GAO BO，et al. Combat efficiencevaluation for electro- optical countermeasure sstems in joint operations[J]. Optics & Optoelectronic Technolog，2013，11（5）：52-55.（in Chinese）

[8]张宪，张国春.兰彻斯特方程损耗系数估算方法研究[J].系统仿真学报，2011，23（8）：1583-1586. ZHANGIAN，ZHANG GUOCHUN. Research on Lanchester attrition-rates coefficient estimation[J]. Journal of Sstem Simulation，2011，23（8）：1583-1586.（in Chinese）

[9]乔林峰，胡浩然，王俊.兰彻斯特方程的参数取值与计算[J].舰船电子工程，2011（8）：49-51. QIAO LINFENG，HU HAORAN，WANG JUN. Parameter values and calculation of Lanchester equations[J]. Ship Electronic Engineering，2011（8）：49-51.（in Chinese）

[10]陈向勇，井元伟，李春吉，等.一种基于Lanchester方程的交战取胜最优策略[J].控制与决策，2011，26（6）：945-948. CHENIANGONG，JINGUANWEI，LI CHUNJI，et al. Optimal strategies for winning in militarconflicts based on Lanchester equation[J]. Control and Decision，2011，26（6）：945-948.（in Chinese）

CONG Hong-ri, WU Fu-chu, CHEN Deng-an
（Department of Command, NAAU,antai Shandong 264001, China）

Abstrraacctt:: The significance, purpose and basic methods of defense operation were analzed, on this base, bdecomposing the destroing coefficient of Lanchester equation, the Lanchester equation containing defense was set up, and the calculat⁃ing eample was offered. In the end, its influences on dogfall condition and operating intensitwere analzed briefl.

作者简介：丛红日（1966-），男，副教授，博士。

收稿日期：2014-10-16；

DOI:10.7682/j.issn.1673-1522.2015.02.021

文章编号：1673-1522（2015）02-0187-04

文献标志码：A

中图分类号：E843

修回日期：2015-01-06