铜团簇(Cu)n(n=2~7)的密度泛函理论研究

苏学军，刘存海，张　勇（海军航空工程学院基础实验部，山东烟台264001）



铜团簇(Cu)n(n=2~7)的密度泛函理论研究

苏学军，刘存海，张勇
（海军航空工程学院基础实验部，山东烟台264001）

摘要：应用密度泛函理论的B3LP方法，在6-31G（d）和6-31++G（d）基组水平上对铜团簇(Cu)n（n=2~7）进行了研究，计算得到了铜团簇的各种稳定构型、总能量、团簇束缚能，以及n=4时铜团簇的红外振动光谱。通过能量最小化原理，确定了各尺寸铜团簇的最稳定构型，并利用二阶差分和分裂能理论，讨论了6种最稳定结构的生长规律，结果表明，n=4时的团簇结构最为稳定，具有明显的幻数特征，n=5时的团簇结构出现区域不稳定的特性。关键词：密度泛函理论；团簇；二阶差分；红外光谱

原子分子团簇，简称团簇（Cluster），是由几个乃至数千个原子、分子或离子通过物理或化学结合力组成的相对稳定的微观或亚微观聚集体。在团簇的研究中，通常采用实验和计算机模拟2种手段，但在实际情况下，随着团簇原子数目的增大，实验要求增高，实验比较困难，目前的研究主要集中在小团簇上[1-3]。因此，对大原子、分子团簇，首先在理论上确定其构型和能量就显得十分重要。应用计算机模拟方法研究团簇的结构、稳定性和能量等性质，能弥补目前实验手段的不足，有助于认识团簇在纳米尺寸上的几何结构及其稳定性，对纳米材料的设计具有重要的指导意义。铜团簇是很好的导电材料，它具有特殊的几何结构和奇异的物理化学性质，常被作为新型红外隐身材料的重要组成部分，这也使对铜团簇的研究成为各国研究的重点[4]。对铜团簇的研究中，在实验方面，Knickelein等人测量了中性铜团簇的离化势并且发现了铜团簇存在电子壳层结构[5]；Spasov等人使用极限碰撞引发分裂的方法研究了带负电铜团簇(Cu)n（n=2~7）的结合能[6]；李公平等利用铜团簇束在硅上碰撞沉积的方法，获得了Cu/P-Si(111)薄膜，并对薄膜表面能谱进行了分析[7]；曹博等对低能铜团簇束在Si(111)上成膜铜在硅中的扩散问题进行了研究[8]。目前对团簇的结构和结合能的理论研究中，使用的方法大致分为密度泛函（DFT）方法、蒙特卡洛方法（MC）方法、分子动力学（MD）方法以及从头计算（Ab initio）方法几种。

密度泛函理论[9]是用电子密度来处理多电子体系，已被广泛应用于计算化学、物理等领域，可成功地预测和解释各种材料中存在的现象。本文运用Gaussian 09计算程序，在B3LP/6-31G（d）和6-31++G（d）基组水平上研究了铜团簇(Cu)n（n=2~7）的各种可能构型进行了理论上的研究，得到了它们的稳定构型；然后，通过频率计算验证了构型的稳定性，并对其结构特点、生长规律和红外振动光谱进行了初步探讨。本文结果也将为实验上进一步研究铜团簇的结构和形成机理提供理论上的依据。

1　计算方法

运用Gaussian 09程序，首先在HF/STO-3G水平上对由Gauss View和ChemOffice软件构建的团簇初始构型进行初步结构优化；然后，用B3LP/6-31G（d）方法对所得构型进行最终结构优化和频率计算；最后，对计算所得的各种团簇构型进行频率分析，确定构型为稳定构型，并得到了红外振动光谱。本文中，能量计算是在B3LP/6-31++G（d）水平上进行的，零点能计算采用0.980 4[10]经验值进行修正，频率计算采用0.961 3[11]的修正因子进行矫正。

2　铜团簇(Cu)n（n=2　~7　）的稳定结构

通过计算，得到了在不同初始构型下(Cu)n（n=2~7）的各种稳定结构。

n=2时，铜团簇只有1种构型，分子构型具有哑铃结构，如图1所示。两铜原子之间键长为2.024Å，团簇结合能为2.675eV。

n=3时，铜团簇具有2种构型，如图1所示。3a具有正三角形结构，任意两原子之间的间距为2.162Å，团簇结合能为5.326eV。3b呈现出一种链式结构，相邻两原子之间的间距为2.069Å，键角∠1Cu2Cu3Cu为160°，与3a相比其团簇结合能略小，为4.996eV。此外，一般而言，同分异构体之间，总能量越低越稳定，3a构型的总能量要低于3b总能量，3a较3b略稳定。

图1　n=2、3时铜团簇结构Fig.1 Structures of ammonia clusters for n=2 and n=3

n=4时，铜团簇具有4种构型，如图2所示。4a具有正四面体结构，任意两原子之间的间距为2.098Å，团簇结合能为7.779eV。4b是在正三角形结构基础上外接一铜原子形成的平面结构，构型以2Cu和3Cu连线为对称轴呈现良好的左右对称性，2Cu和3Cu之间的间距为2.154Å，2Cu-4Cu和3Cu-4Cu键长都为2.174Å，键角∠2Cu4Cu3Cu为59.4°，键角∠4Cu2Cu3Cu 为60.3°。从团簇能量角度来看，4a较稳定。

n=5时，铜团簇具有2种稳定的同分异构体构型，见图2。5a具有双三棱锥结构，它是在一四面体外侧连接一铜原子构成的，4Cu和5Cu两原子呈现出上下对称结构。构型中，1Cu-2Cu、1Cu-2Cu和1Cu-3Cu之间的距离均为2.213Å，其余铜原子间距均为2.233Å。5b构型中铜原子近似处在同一平面内，构型具有好的左右对称结构。其中，4Cu-5Cu和3Cu-5Cu之间的间距分别为2.163Å和2.166Å，而4Cu-3Cu和1Cu-4Cu之间间距分别为2.221Å和2.191Å。从能量角度来看，两同分异构体中5a的总能量较5b的低，故5a的构型较5b稳定。

图2　n=4、5时铜团簇结构Fig.2 Structures of ammonia clusters for n=4 and n=5

n=6时，有4种同分异构体，如图3所示。6a具有正五棱锥结构，它是在一平面环状结构外侧连接一铜原子构成的，中心铜原子与环状结构中铜原子之间的键长均为2.17716Å，环状结构中任意相邻的两铜原子之间的键长为2.251Å。6b是在由5个铜原子所构成的类平面结构上方连接一铜原子构成的，它呈现出好的左右对称特性。结构中，5Cu-3Cu和5Cu-4Cu之间间距均为2.168Å，5Cu-1Cu之间的间距为2.437Å，而3Cu-2Cu、2Cu-1Cu和3Cu-1Cu之间的间距分别为2.179Å、2.182Å和2.208Å。6c具有近似平面结构。6d具有舟型结构，它是在一双三棱锥外侧连接一铜原子构成的，结构呈现出优良的对称性。结构中，除3Cu-2Cu为2.202Å以外，2Cu、3Cu、4Cu和5Cu 4个铜原子彼此之间所形成的键长均为2.236Å；结构中，4Cu-1Cu 和5Cu-6Cu之间的间距均为2.242Å，1Cu、5Cu分别与2Cu、3Cu之间的间距均为2.305Å。在4种同分异构体中，由于6d的总能量最低，故结构最稳定。

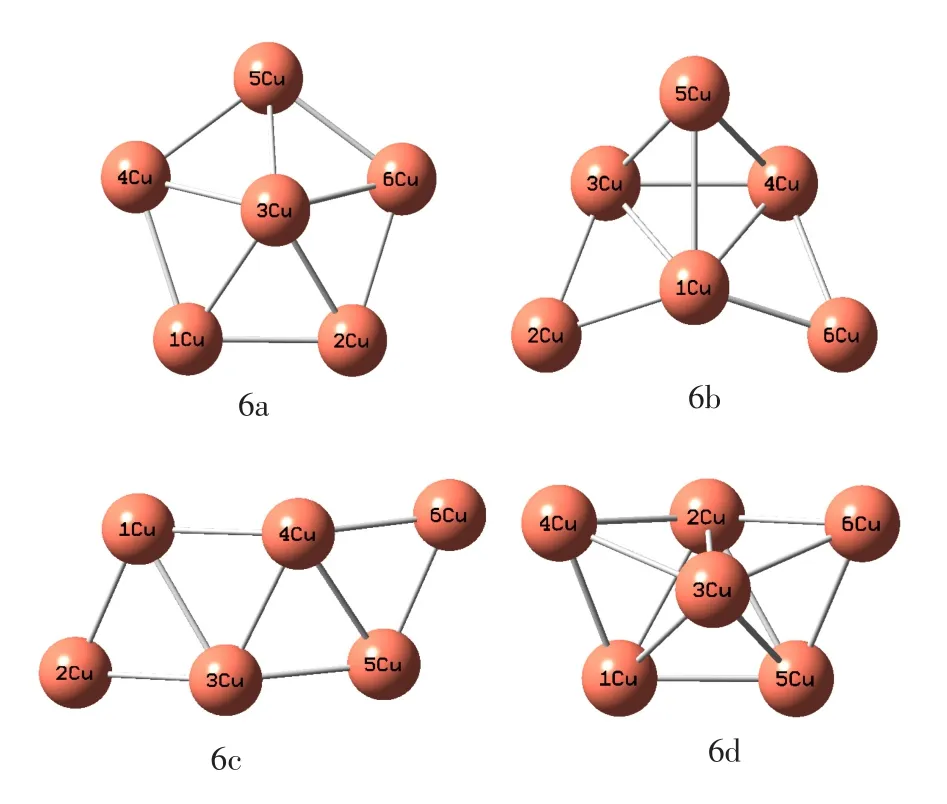
图3　n=6时铜团簇结构Fig.3 Structures of ammonia clusters for n=6

图4给出了n=7时铜团簇的3种同分异构体。7a具有较好的左右对称结构，它是在一双棱锥结构的基础上外接2个铜原子形成的。结构中，2Cu分别与3Cu 和7Cu原子之间的间距均为2.216Å，4Cu与3Cu和7Cu原子之间的间距均为2.314Å，4Cu与5Cu和6Cu原子之间的间距均为2.217Å，5Cu-6Cu和7Cu-6Cu原子之间的间距均为2.216Å。7b具有双五棱锥结构，对称性好。结构中，除5Cu-1Cu键键长为2.382Å外，其余键长均为2.260Å。7c是在一舟型结构基础上外接一铜原子形成的。结构中，5Cu- 6Cu键键长为2.21931Å，较1Cu-3Cu键键长略短，7Cu-2Cu和7Cu-1Cu两键键长分别为2.180Å和2.178Å，3Cu-5Cu键键长为2.222Å，3Cu-2Cu和3Cu-4Cu两键键长分别为2.333Å和2.294Å，5Cu-2Cu和5Cu-4Cu两键键长分别为2.292Å和2.282Å。从能量角度来看7b结构最稳定。

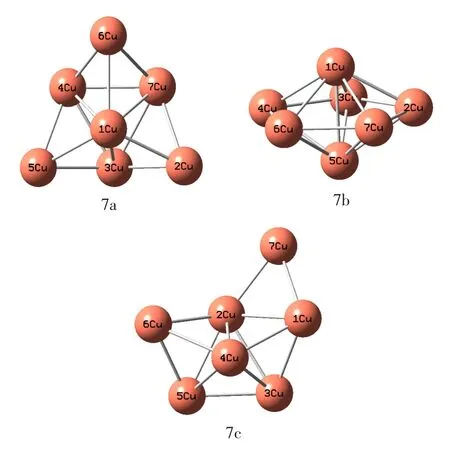
图4　n=7时铜团簇结构Fig.4 Structures of ammonia clusters for n=7

由以上分析看出，在不同尺寸的铜团簇（Cu）n（n=2~7）的各种构型中，最稳定构型为n=2，3a，4a，5a，6d和7b。

3　铜团簇稳定性研究

为了研究不同尺寸中铜团簇最稳定构型的生长规律，对铜团簇总能量的二阶差分和分裂能进行了分析[12]。二阶差分和分裂能是一个体现团簇相对稳定性的物理量，它们的值越大表明团簇的稳定性越强[13]。二阶差分和分裂能的计算公式分别为：式（1）、（2）中：Δ2E和D(n,n-1 )分别为团簇的二阶差分和分裂能；E为团簇总能量。

铜团簇的二阶差分Δ2E和分裂能D(n,n-1 )随团簇尺寸n的变化规律如图5所示。分析发现，随着(Cu)n（n=2~7）团簇的尺寸的增加，团簇的二阶差分呈现出波动，在n=4时出现峰值，表明Cu4稳定性比相邻尺寸的团簇更加稳定，而当n=3和5时，铜团簇二阶差分出现谷值，表明其比相邻尺寸的团簇更不稳定。对铜团簇的分裂能而言，当n=4时出现峰值，表明它的稳定性比相邻的尺寸的团簇的稳定性要高。综合铜团簇的二阶差分和分裂能的分析，二阶差分和分裂能都表明n=4时，团簇的结构相对稳定，有明显的幻数特性[14]。而n=5时，二阶差分和分裂能均呈现出区域最小值，因而其结构稳定比相邻尺寸的团簇比较低。

图5　(Cu)n（n=2~7）团簇的二阶能量差分和分裂能Fig.5 Second order differences and the fragmentation energies of the (Cu)n（n=2~7）clusters

4　铜团簇（Cu）4　的红外光谱研究

通过对铜团簇总能量的二阶差分和分裂能的分析，发现了n=4时，铜团簇4a构型表现出了奇特的幻数特性。为了进一步了解铜团簇（Cu）4的特性，对其红外光谱的特性进了研究，如图6所示。一般而言，红外吸收强度决定于振动时偶极矩变化的大小。若振动过程中偶极矩变化较大，则跃迁几率就会越大，光谱强度相应就会较强；若分子在振动过程中偶极矩变化较小，则跃迁几率相应较小，红外光谱强度也就会较弱。

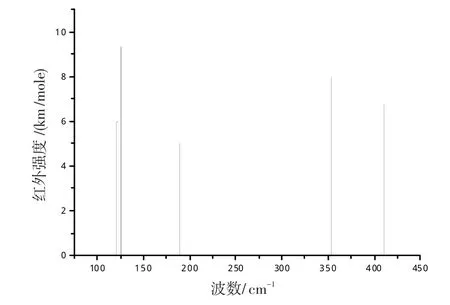
图6　n=4时铜团簇的红外光谱Fig.6 Infra-red spectrum of the copper cluster for n=4

通过分析发现，铜团簇（Cu）4红外光谱的谱线主要集中在0~450 cm-1区域，分子的振动模式主要包括化学键的伸缩振动、弯曲振动以及整体构型的变形。光谱中最强峰出现在126 cm-1位置，具有二重简并特性，谱线分别由3Cu-2Cu键的伸缩振动、1Cu-4Cu键和1Cu-3Cu键的不对称伸缩振动引起的。而铜团簇（Cu）4构型的整体收缩振动在189 cm-1位置造成一谱线，它也是红外光谱的最弱峰。1Cu-4Cu键和2Cu-3Cu键的面内弯曲振动在121 cm-1位置出现一较强共振峰。353 cm-1和410 cm-1位置谱线分别是由1Cu-2Cu键的伸缩振动和以4Cu原子为定点的3个化学键的对称弯曲振动造成的。

5　结论

在密度泛函理论的基础上，利用Gaussian 09程序计算得到了铜团簇(Cu)n（n=2~7）的各种稳定构型，并对各构型的特点进行了简单讨论，确定了各种尺寸的铜团簇的最稳定构型，并应用二阶差分和分裂能理论研究了不同尺寸的铜团簇中最稳定构型的稳定性随n的变化规律。发现：在n=4时的团簇结构最为稳定，具有幻数结构；在n=5时二阶差分和分裂能均取极小值，说明这个结构不稳定。此外，还对铜团簇（Cu）4的红外光谱的分布规律和形成特点进行了讨论，对红外光谱中出现的各条谱峰进行归属和指认。

参考文献：

[2]ZANG QING，CAO MAOQI，IEANG，et al. Research progress of hdrogen clusters and their applications[J]. Journal of Atomic and Molecular Phsics，2014，31（2）：50-56.

[4]KARL JUG. Structure and abilitof small copper cluster [J]. Journal of ChemistrPhsics，2002，15（3）：142-146.

[5]KNICKELBEIN M B. Electronic shell structure in the ionization potentials of copper clusters[J]. ChemistrPhsics Letters，1992，192（1）：129-134.

[6]SPASOV V A，LEE T H，ERVIN K M. Threshold collision-induced dissociation of anionic copper clusters and copper cluster monocarbonls[J]. Journal of Chemical Phsics，2000，112（4）：1713-1721.

[7]李公平，何山虎，丁宝卫，等.铜团簇束在硅上碰撞沉积的薄膜形貌和方块电阻[J].兰州大学学报：自然科学版，2004，40（5）：31-33. LI GONGPING，HE SHANHU，DING BAOWEI，et al. The morphologand rectangular resistance of films formation bCu cluster beam collided with and deposited onto Si substrate[J]. Journal of Lanzhou Universit：Natural Science，2004，40（5）：31-33.（in Chinese）

[8]曹博，李公平，盖志刚，等.低能铜团簇束在Si（111）上成膜铜的扩散[C]//第一届中国核技术及应用研究学术研讨会.上海，2006：52-53. CAO BO，LI GONGPING，GAI ZHIGANG，et al. Diffusion of low-energCu cluster beam in Si（111）in Cu thin films[C]//The First Smposium on Chinese Nuclear Technologand Application. Shanghai，2006：52-53.（in Chinese）

[9]MIEHLICH B，SAVIN A，STOLL H，et al. Results obtained with the correlation energdensitfunctional[J]. ChemistrPhsics Letters，1989，157（3）：200-206.

[10]WONG M W，WIBERG K B，FRISCH M J. Hartree-Fock second derivatives and electric field properties in a solvent reaction field：Theorand application[J]. Journal of Chemical Phsics，1991，95（12）：8991-8996.

[11]FORESMAN J B，FRISCH A. Eploring chemistrwith electronic structure methods[M]. 2nd ed. Pittsburgh：Gaussian Inc.，1996：68-69.

[12]王广厚.团簇物理学[M].上海：上海科学技术出版社，

2003：87-88. WANG GUANGHOU. Cluster phsics[M]. Shanghai：Shanghai Scientific & Technical Press，2003：87-88.（in Chinese）

[13]王广厚.团簇物理的新进展[J].物理学进展，1994，14

（2）：121-172. WANG GUANGHOU. New progress in cluster phsics [J]. Progress in Phsics，1994，14（2）：121-172.（in Chinese）

[14]王广厚.原子团簇的稳定结构和幻数[J].物理学进展，

2000，20（1）：53-94. WANG GUANGHOU. Stable structures and magic numbers of atomic clusters[J]. Progress in Phsics，2000，20 （1）：53-94.（in Chinese）

Abstrraacctt:: The copper cluster (Cu)n( n=2~7) was studied at the 6-31G(d) and 6-31++G(d) basis sets level, using the B3LP method of densitfunctional theor. Through calculation, different structures, energies, binding energies and infrared spectrum of copper cluster for n=4 were gained. Using minimize energtheor, the most stable structure of different size of copper cluster was confirmed. Finall, the second differential theorand dissociation theorwere used to discuss the growth law of sikind of structures in the most stable copper clusters. The results showed that the cluster for n=4 was the most stable one and had the feature of magic number. But the stabilitof the cluster for n=5 had the feature of local minimum.

收稿日期：2014-12-28；修回日期：2015-02-01

作者简介：苏学军（1967-），男，教授，硕士。

DOI:10.7682/j.issn.1673-1522.2015.02.017

文章编号：1673-1522（2015）02-0174-04

文献标志码：A

中图分类号：O641