未知互耦条件下混合信号波达方向估计
潘 哲,毛维平(.海军装备部驻天津地区军事代表局,天津300000;.海军航空工程学院7系,山东烟台6400)
未知互耦条件下混合信号波达方向估计
潘哲1,毛维平2
(1.海军装备部驻天津地区军事代表局,天津300000;2.海军航空工程学院7系,山东烟台264001)
摘要:阵列天线互耦对导向矢量的扰动以及信号相干性对数据协方差矩阵造成的秩损,使得基于子空间正交性原理的超分辨波达方向估计(Direction-of-Arrival,DOA)算法性能恶化,甚至失效。针对这一问题,提出一种在相干与非相干信号混合状态下无需阵列互耦补偿的特征矢量平滑DOA估计算法。该算法对部分阵元接收数据的协方差矩阵特征分解,将得到的特征矢量平滑处理后构造等效协方差矩阵,抑制阵列互耦影响的同时完成混合信号DOA估计。在阵列互耦和信号相干性均未知的条件下,正确估计了信号DOA,无需互耦参数估计或补偿。计算机仿真结果验证了算法的有效性。
关键词:阵列信号处理;波达方向;相干;互耦
MUSIC(Multiple Signal Classification)、ESPRIT (Estimation of Signal Parameters Via Rotational Invariance Techniques)等超分辨DOA估计算法突破了瑞利限的约束,分辨力高,在过去几十年间被广泛应用于雷达、声纳、无线通信等领域,它们以理想的阵列流形和准确的子空间划分为前提。然而,阵元间的互耦对阵列流形的扰动是不可避免的[1],信号的多径传播导致子空间划分与真实子空间不符[2],这些因素制约着空间谱估计算法走向实际应用。
针对阵列互耦补偿与信号解相干问题,文献[3]分别利用矩阵重构、空间平滑等技术,实现了信号解相干,但都没有考虑阵列互耦的影响。文献[4]考虑了阵列互耦的影响,并对互耦进行了抑制和补偿,但不适用相干信号。文献[5]提出一种交互迭代最大似然估计算法,解决了信号多径传播和阵列互耦影响下的DOA估计问题,但需要多维非线性搜索,增大运算量的同时,其全局收敛性也无法保证。文献[6]提出一种阵列互耦影响下混合信号非迭代的分步估计算法,但在估计相干信号以前,须先估计非相干信号,并利用非相干信号的估计值得到互耦系数。文献[7]利用互耦矩阵的特点,基于空间平滑算法实现了互耦抑制和相干信号DOA估计。
本文考虑阵列互耦的影响,提出了一种修正的特征矢量平滑解相干算法,在无需互耦补偿的情况下,估计相干与非相干混合信号的波达方向。算法在文献[4]的基础上,截取部分阵元的接收数据,求得数据协方差矩阵,利用特征分解所得特征矢量,经平滑处理后构造解相干等效协方差矩阵,达到阵列互耦自抑制的同时,实现信号DOA估计。
1 问题的描述
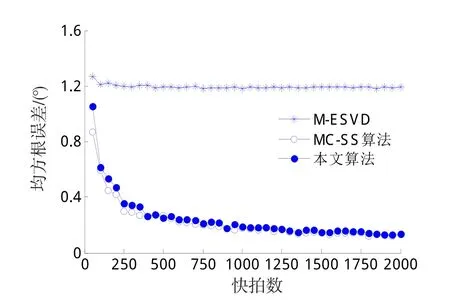
假设载频已知的M个远场窄带信源si(t) (i=1,2,…,M)辐射到N(N>M)个各向同性的均匀线阵上。信源由L(L≥1)组相干信号组成,组间相互独立,设第l组有pl(pl≥1,l=1,2,…,L)个信源,则,θln(n=1,2,…,pl)表示第l组中第n个信号的入射方向。噪声为零均值加性高斯白噪声,噪声之间、噪声与信号之间均统计独立。以第1个阵元为参考阵元,考虑阵列互耦,设有m个非零互耦系数,则互耦矩阵可表示为[4]:式中,0<|cm|<…<|c2| 阵列输出的矢量形式可表示为[4]:式(2)中:A=[A1,A2,…,AL]为N×M阶阵列流形矩阵, B=blkdiag{b ,b,…,bL}为M×L阶块对角阵,为pl×1阶衰落系数矢量;;为N×1阶阵列噪声矢量。 以MUSIC算法为例,求得数据协方差矩阵:式(3)中:E[∙]表示期望算子;为噪声功率。 2.1互耦自抑制 由式(1)可知,互耦矩阵的第m行到第N-m+1行的非零元素完全相同,仅是处在矩阵中的位置不同。定义一个选择矩阵[4]:式(5)中:K≥M;N≥2K+2m-1。 将式(6)展开可得: 式(11)表明互耦系数已经从原阵列流形矩阵CA中分离出来,并入到等效的入射信号l(t)=c(θln)ρlnsl(t)中。新的阵列流形矩阵没有互耦扰动,而且具备Vandermonde矩阵形式。因此,选择部分阵元输出的数据矢量,可利用互耦矩阵的特殊结构,实现互耦自抑制。 2.2特征矢量平滑解相干算法 利用式(11)的数据矢量计算协方差矩阵: 由文献[8]中定理:假设M个远场窄带信源辐射到N(N>M)个阵元组成的阵列上,阵列流形矩阵秩为M,信号协方差矩阵秩s为L(L≤M),若噪声协方差矩阵n为满秩矩阵,则存在如下线性关系:式中,ek表示大特征值对应的特征矢量(简记为:大特征矢量)。 当入射信号完全相干时,大特征矢量只有一个。它包含所有入射信号信息,常规特征矢量奇异值解相干算法(ESVD)选择最大特征矢量求解DOA,这是完全可取的。但当入射信号为不相干与相干信号混合时,大特征值不止一个,对应的特征矢量也不止一个,如果依然选择最大特征矢量来求解,最大特征矢量并没有包含所有入射信号信息,这样必然造成漏估计(见仿真1)。利用式(14)的矢量得到一个新矢量: 由式(15)可知,所有的大特征矢量都被利用,新矢量e包含所有入射信号信息,不会造成漏估计。 根据式(18),构造矩阵: 由文献[9]可知,当平滑次数不小于相干信号个数时,矩阵R的秩等于入射信号个数,与信号的相干性无关。式(19)只利用了前向平滑。同理,可利用前后向平滑构造矩阵,这里不再赘述。利用式(19)重构的矩阵,结合经典空间谱估计算法(MUSIC、ESPRIT等),即可估计相干信号的DOA。 仿真1:验证混合信号对本文算法和常规特征矢量奇异值分解算法的影响。当入射信号完全相干时,本文算法就是常规特征矢量奇异值算法。因此,只讨论相干与非相干混合的入射信号。4个远场窄带信号分别以到达角(-10°、10°、30°、50°)入射到阵元数为15,阵元间距为半波长的均匀线阵上。其中,30° 和50°入射的2个信号是相干信号,其余为不相干信号,由特征分解理论,协方差矩阵分解后会得到3个大特征矢量。设非零的互耦系数个数为3,分别为c1=1、c2=0.8+0.4i和c3=0.5-0.3i,信噪比为20 dB,快拍数为500次。利用互耦自抑制后的数据,基于MUSIC搜索空间谱,搜索精度设为0.5°,本文算法以及分别利用每个大特征矢量奇异值分解算法的估计结果如图1所示。第1个和第2个大特征矢量能正确估计2个非相干信号,却没有估计出相干信号的入射角。第3个大特征矢量主要包含了2个相干信号的信息,正确估计出了相干信号,但却漏估计了2个非相干信号。本文算法综合利用的不同大特征矢量的信息,准确估计了所有信号的入射角。 仿真2:验证算法的有效性。仿真条件如仿真1,将本文算法与不考虑互耦的修正矢量奇异值分解算法(记为M-ESVD)、基于空间平滑的互耦抑制与解相干算法(记为MC-SS算法)作对比,见图2。由图2可知,M-ESVD算法不考虑互耦的影响,DOA估计偏差较大,而且角度越大,偏差越大,这一点可通过导向矢量表达式中的正弦因子来解释。本文算法和MC-SS算法都准确估计了信号DOA,在高信噪比条件下,MC-SS算法谱峰更尖锐,表现出更好的估计性能,但在低信噪比时,本文算法性能更好(见仿真3)。 图1 不同特征矢量重构矩阵的DOA估计Fig.1 DOAestimation via reconstructed matrices of different eigenvectors 图2 不同算法的估计性能Fig.2 Performance of different algorithms 仿真3:算法对信噪比与快拍数的敏感程度。阵列模型和入射信号如仿真1,快拍数为500次,信噪比从0~30 dB,步进步长为1 dB,在每个信噪比条件下基于ESPRIT原理进行100次Monte-Carlo仿真试验,DOA估计的均方根误差随信噪比(SNR)的变化结果如图3所示。 图3 均方根误差随信噪比的变化Fig. 3 RMSE of DOAversus SNR 由图3可知,M-ESVD算法不考虑互耦影响,其均方根误差较大,而且并不会随信噪比的增大而减小。因此,阵列互耦对DOA估计的影响是不容忽视的。本文算法在低信噪比时性能要优于MC-SS算法,随着信噪比的增大,两者性能相当。在相同的仿真条件下,固定信噪比SNR = 10 dB,快拍数为50~2 000次,步进步长为50,在每个快拍数条件下基于ESPRIT原理进行100次Monte-Carlo仿真试验,结果如图4所示。图4同样表明,如果不考虑互耦,随着快拍数的增加,估计性能并没有得到改善。在SNR=10dB时,无论是在少量快拍还是在大快拍数条件下,本文算法与MC-SS算法性能相当。 图4 均方根误差随快拍数的变化Fig.4 RMSE of DOAversus snapshots 本文针对阵列互耦条件下相干与非相干混合信号的DOA估计问题,提出一种免互耦补偿的特征矢量平滑解相干算法。算法利用互耦矩阵的内在特点实现阵列互耦自抑制,无需任何互耦补偿措施。分析了常规矢量奇异值算法在混合信号条件下的局限性,提出的修正算法有效地弥补了常规算法的缺点,能同时估计出混合信号的入射角。在低信噪比时,本文算法较已有算法具有更小的估计均方根误差,计算机仿真结果验证了算法的有效性。 参考文献: [3]HAN F M,ZHANGD. An ESPRIT-like algorithm for coherent DOA estimation[J]. IEEE Antennas and Wireless Propagation Letters,2005,4:443-446. [5]BAO Q,KO C C,ZHI W. DOA estimation under unknown mutual coupling and multipath[J]. IEEE Trans. on Aerospace and Electronic Sstems,2005,41(2):565–573. [8]CADZOW J A,KIMS,SHIUE D C. General direction of arrival estimation:a signal subspace approach[J]. IEEE Transactions on Aerospace and Electronic Sstems,1989,25(1):31-46. DDOOAA EEssttiimmaattiioonn ooff MMiieedd SSiiggnnaallss UUnnddeerr UUnnkknnoowwnn MMuuttuuaall CCoouupplliinngg PAN Zhe1, MAO Wei-ping2 Abstrraacctt:: Performance of high resolution direction-of-arrival (DOA) estimation algorithms based on the orthogonalitof subspaces is degraded barramanifold perturbation resulted from mutual coupling (MC) and rank loss of covariance ma⁃tricaused bsignal coherenc. In this paper, an eigenvectors smoothing direction finding method, without anMC com⁃pensation, was proposed for coherent and non-coherent mied signals under unknown MC. The method automaticallsup⁃pressed the effects of unknown MC ban equivalent covariance matrireconstructed through eigenvectors smoothing. The DOAs of mied signals could be estimated with the equivalent covariance matri. Without anarracalibration, the pro⁃posed algorithm achieved a favorable accuracof DOA estimation under unknown MC irrespective of signal coherenc. The simulation results demonstrated the validitof the proposed method. 作者简介:潘哲(1964-),男,高工,大学。 基金项目:国家自然科学基金资助项目(601102165) 收稿日期:2014-10-11; DOI:10.7682/j.issn.1673-1522.2015.02.002 文章编号:1673-1522(2015)02-0106-05 文献标志码:A 中图分类号:TN911.23 修回日期:2015-01-21
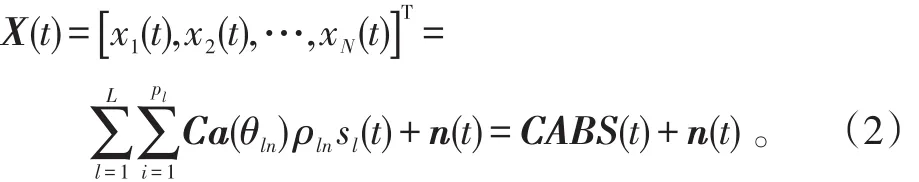


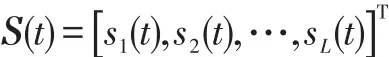


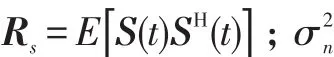
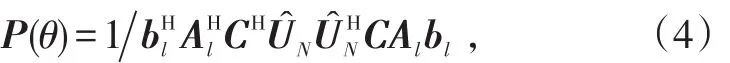
2 算法的提出
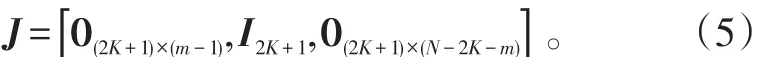






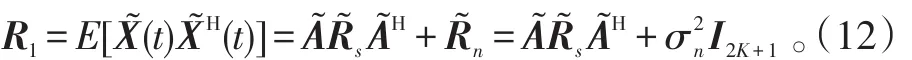



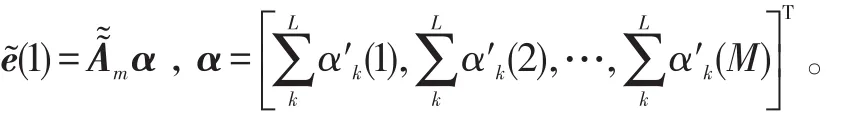
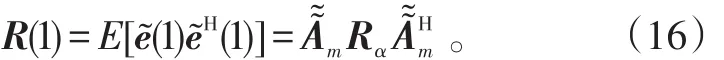



3 数值仿真



4 结论
(1. MilitarRepresentatives Bureau of NED in Tianjin, Tianjin 300000, China; 2. No.7 Department, NAAU,antai Shandong 264001, China)

