一种基于协方差矩阵重构的相干信源DOA估计算法
刘晓娣,周新力,肖金光,张 烨(海军航空工程学院电子信息工程系,山东烟台264001)
一种基于协方差矩阵重构的相干信源DOA估计算法
刘晓娣,周新力,肖金光,张烨
(海军航空工程学院电子信息工程系,山东烟台264001)
摘要:针对空间相干信源的波达方向估计问题,提出了一种基于协方差矩阵重构的TSVD-ESPRIT算法。它利用包含所有信源信息的特征向量构造Toeplitz协方差矩阵,避免了阵列有效孔径的损失,分辨率高且稳定性好;并且利用ESPRIT算法代替MUSIC算法进行DOA估计,避免了谱峰搜索,大大降低了计算量。数据仿真和分析证明了该算法的正确性和有效性。
关键词:DOA估计;协方差矩阵;ESPRIT;相干信源
波达方向(Direction of Arrival,DOA)是阵列信号处理的一个热点问题,在通信、雷达、声纳等领域有重要应用[1-4]。实际应用中,受多径效应或电磁干扰等影响,信号到达天线阵列时往往产生相干,接收数据的空间协方差矩阵产生秩损失,传统的DOA算法如多重信号分类[5](Multiple Signal Classification,MUSIC)、利用旋转不变性进行信号参数估计[6](Estimation of Signal Parameter Via Rotational Invariance Techniques,ESPRIT)等在相干环境中失去效用。针对相干信号源的DOA估计,很多算法相继被提出,这些算法总体上分为解相干预处理和基于解相干基础上的DOA估计(即传统的DOA估计)2个部分。目前,解相干预处理算法主要有2类[7]:一类是降维法,如空间平滑类算法、矩阵重构算法;另一类是非降维处理法,如Toeplitz法。降维法以牺牲阵列有效孔径为代价获得解相干能力,降低了算法的分辨率,而非降维处理法往往会产生较大的估计偏差。为此,文献[8-9]综合考虑2类算法,重构协方差矩阵,在一定程度上提高了解相干的性能。而这些算法大都以MUSIC作为DOA估计处理技术[10],由于MUSIC需要进行谱峰搜索,致使算法的运算量较大。
为了解除信号源的相干性,不损失阵列有效孔径,同时避免谱峰搜索,本文在文献[10]的基础上提出了一种基于协方差矩阵重构的TSVD-ESPRIT算法。该算法首先通过奇异值分解(Singular Value Decomposition,SVD)获得包含所有信号信息的特征向量;然后,利用所得的特征向量构造一个Toeplitz协方差矩阵,重构的协方差矩阵维数等于阵元个数,对其进行特征值分解即可得到信号子空间和噪声子空间;最后,利用ESPRIT进行DOA估计。与文献[8,10]和传统的SVD算法相比,该算法没有阵列孔径损失,分辨率高;与文献[9]相比,该算法用ESPRIT代替MUSIC,且不需构造多个Toeplitz矩阵,复杂度大大降低。
1 信号模型
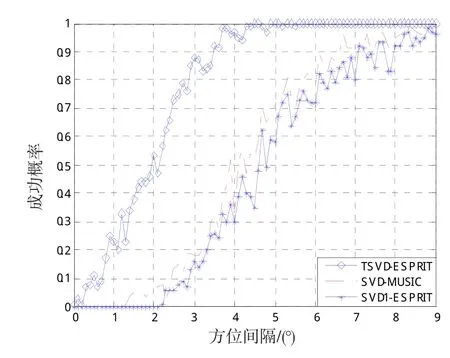
假设一个标准均匀线阵,包含N个相同的全向阵元,阵元间距满足“半波长条件”,即d≤λ/2(λ是入射波长)。现有M个远场窄带信号(M 阵列接收的数据可以表示为式(2)中:A=[a(θ1),a(θ2),…,a(θM)]为阵列流型矩阵,其中,a(θ)=[1,e-j 2 λπdsinθi,…,e-j 2 λπd(N-1)sinθi]T为阵列接收第i个 i信号时的导向向量;S(t)=[s1(t),s2(t),…,sM(t)]T为信号向量,N(t)=[n1(t),n2(t),…,nN(t)]T为阵列接收噪声向量。 根据上述假设,阵列的协方差矩阵表示为:式(3)中:E{∙}表示统计期望;RS=E{S(t)SH(t) }表示信号协方差矩阵;RN=σ2I表示噪声的协方差矩阵,σ2表示噪声功率,I表示单位矩阵。 在信号统计独立的情况下,rank(R)等于信号个数M,对R进行特征值分解可以得到相互正交的信号子空间和噪声子空间;而在相干环境下,相干信号对应的信号特征向量将恶化转变到噪声子空间,rank(R)小于信号个数M,从而无法利用传统的算法对相干信号进行DOA估计。 对于相干信源DOA的估计,本文首先利用包含所有信号信息的数据矢量,构造一个秩等于信号个数M的Toeplitz矩阵,实现解相干的目的;而后,利用ESPRIT算法进行DOA估计。 2.1解相干预处理 定理1:[11]假设M(M≤N-1)个平面波入射到N元天线阵上,阵列流型矩阵A的秩为M,信号矩阵RS的秩为K(K≤M),噪声协方差矩阵RN为满秩矩阵,则有 如下线性关系成立:式(4)中:ek(1≤k≤K)为对应于K个信号特征值λ1≥λ2…≥λK>σ2的信号特征向量;αk(i)为线性组合因子。 根据上述假设RN=σ2I,式(4)可简化为: 由定理1可知,在理想高斯白噪声条件下,无论入射信号是否相干,对应大特征值的信号特征向量是各信源导向向量的一个线性组合,即包含了所有信号方向信息。在此,对大特征值对应的特征向量取均值:式中, 利用eˉ构造Toeplitz矩阵: 将式(6)代入式(7)得: 式(8)中,,显然rank(Rα)=M。 又阵列导向向量矩阵A为Vandermonde矩阵,rank(A)=M,所以ARαAH的秩为M,即rank(G)=M。这表明无论入射信号是否相干,新构造的协方差矩阵G的秩都等于信号数,从而达到了“解相干”的目的。对G进行特征值分解可得到M个大特征值和N-M个小特征值,它们对应的特征向量分别为…,uM,uM+1,uM+2,…,uN,则US=[u1,u2,…,uM]的各列可张成信号子空间,UN=[uM+1,uM+2,…,uN]的各列可张成噪声子空间。 2.2 DOA估计 根据2.1中分析所得的信号子空间和噪声子空间,利用ESPRIT进行DOA估计。令阵列流型矩阵 ,其中:a1和aN分别对应A的第一行和最后一行,由阵列流型矩阵的结构可得式中表示包含方向信息的旋转矩阵。 对U进行同样地分解,U=é ê1ùú=éê Fùú,其中u和 SSëUBûëuNû1 uN分别对应US的第一行和最后一行。由阵列流型矩阵的各列也可张成信号子空间,从而必存在一个非奇异矩阵T满足 由式(10)可得:由式(9)、(11)可得式(12)中:( )∙-1表示逆矩阵;( )∙+表示矩阵的Moore-Penrose广义逆。 令显然,Ψ和Φ有同样的特征值,对Ψ进行特征值分解即可得到Φ,从而可估计出各信号的到达角θi(i=1,…,M)。 2.3算法步骤 利用本算法进行相干信源DOA估计的具体步骤: 2)对协方差矩阵R进行特征值分解,取出信号特征向量并根据式(6)求出信号特征向量的均值eˉ; 3)利用eˉ根据式(7)重构协方差矩阵G; 4)对协方差矩阵G进行特征值分解得到信号子空间US;5)利用US得到UB和UF,根据式(13)计算Ψ;6)对Ψ进行特征值分解得到Φ,根据Φ的表达式就可得到对应的入射信号的到达角。 为验证新算法的有效性,利用Matlab进行了数值仿真实验,将本文提出的TSVD-ESPRIT与SVD-MUSIC、文献[10]中的第1种方法SVD1-ESPRIT 3种算法进行比较分析。实验中,接收阵列为均匀线阵,阵元间距为λ 2,背景噪声为与信号不相关的窄带高斯白噪声。每次实验都取200次Monte Carlo实验结果的平均值,数据快拍数为200,SVD-MUSIC功率谱搜素步长为0.01°。仿真中,DOA估计的均方根误差定义为式中,i(n)表示第n次θi的估计值;M表示入射的窄带信号的个数。定义均方根误差θRMSE<0.2°时算法估计成功,成功概率定义为估计成功次数与总实验次数之比。 实验1:2个相干信号,SNR =5 dB,第1个信号从-1°入射到均匀线阵,第2个信号的方位角从0°到9°为间隔变化,每个方位间隔进行200次Monte Carlo实验。分析3种算法的均方根误差θRMSE、成功概率随SNR的变化情况,见图1、2。 图1 成功概率随方位间隔的变化曲线Fig.1 Chang curve of probabilitwith success with angle interval 从图1、2中可以看出,在SNR一定的情况下,3种方法的成功概率、均方根误差皆随方位间隔的增大而增大,其中TSVD-ESPRIT算法的性能优于其他2种算法,这是由于该算法在解相干预处理时避免了阵列有效孔径的损失,使得分辨率提高。 实验2:3个等功率相干信源分别以-15°、5°、15°入射到均匀线阵,阵元数为15,SNR从-10 dB到20 dB以0.5dB的间隔变化,每个SNR进行200次Monte Carlo实验。分析3种算法的均方根误差θRMSE、成功概率随SNR的变化情况。 图3为成功概率随SNR的变化曲线。从图中可以看出,在信源夹角一定的情况下,3种算法的成功概率随SNR的增加而增大,其中TSVD-ESPRIT优于其他2种方法,即使在低信噪比(-10dB≤SNR≤0dB)的情况下,该算法与其他2种算法相比,也具有较高的成功概率。 图3 成功概率随SNR的变化曲线Fig.3 Chang curve of probabilitwith SNR 图4为θRMSE随SNR的变化曲线。随着SNR的增大,3种方法的θRMSE逐渐减小。其中,TSVD-ESPRIT的均方根误差最小,SVD-MUSIC其次,SVD1-ESPRIT误差最大。而当信源完全相干时,SVD-MUSIC和SVD1-ESPRIT的解相干性能是一致的,这证明了在同样情况下,MUSIC算法的估计性能要优于ESPRIT算法[7]。当SNR在4~8dB变化时,TSVD-ESPRIT算法的θRMSE比SVD-MUSIC低约0.05°,表明该算法在计算精度方面优于SVD-MUSIC。同时,因避免了谱峰搜索,在计算速度上也优于SVD-MUSIC。 图4 均方根误差随SNR的变化曲线Fig.4 Chang curve of RMSE with SNR 因此,本文提出的TSVD-ESPRIT算法,对相干信源DOA具有良好的估计性能,且稳定性好,在低信噪比情况下,优势更为明显。 本文在文献[10]的基础上提出了一种估计性能高、稳定性好的TSVD-ESPRIT算法。它利用包含所有信源信息的特征向量构造Toeplitz协方差矩阵,避免了阵列有效孔径的损失,分辨率高且稳定性好;相比传统的SVD-MUSIC的算法,避免了谱峰搜索,降低了运算量。 参考文献: [1]VEEN A,LESHEM A,BOONSTRAA. Arrasignal processing for radio astronom[J]. Eperimental Astronom,2004,17(1):231-249. [2]SALAMEH A,TAVEM N. Conjugate MUSIC for non-circular sources[C]//IEEE International Conference on Acoustics,Speech and Signal Processing. Toulouse. IEEE,2006:877-880. [3]ELLINGSON S W,HAMPSON G A,CHILDERS R K. Argus:a 1-band all-keastronomical surveillance sstem [J]. IEEE Transactions on Antennas and Propagation,2008,56(2):294-302. [5]SCHMIDT R O. Multiple emitter location and signal parameter estimation[J]. IEEE Transactions on Antennas and Propagation,1986,34(3):276-280. [7]王永良,陈辉,彭应宁,等.空间谱估计理论与算法[M].北京:清华大学出版社,2004:11. WANGONGLINAG,CHEN HUI,PENGINGNING,et al. Spatial spectrum estimation theoran method [M]. Beijing:Tsinghua UniversitPress,2004:11.(in Chinese) [8]陈绍炜,魏盈盈,冯晓毅.基于SVD和Toeplitz的高效DOA估计算法[J].西北工业大学学报,2010,28(6):883-886. CHEN SHAOWEI,WEIINGING,FENGIAOI. A new and efficient TSVD algorithm for estimation DOA[J]. Journal of Northwestern Poltechnical Universit,2010,28(6):883-886.(in Chinese) [9]郭艳,刘学亮,李宁,等.基于协方差矩阵重构的DOA估计方法[J].解放军理工大学学报:自然科学版,2012,13 (1):1-5. GUOAN,LIUUELIANG,LI NING,et al. Covariance matrireconstruction approach for DOA estimation of spatial signals[J]. Journal of PLA Universitof Science and Technolog:Natural Science Edition,2012,13 (1):1-5.(in Chinese) [10]张洪顺,徐云林,湛江书.基于信号子空间的ESPRITLike算法在相干DOA估计中的应用[J].通信学报,2010,31(7):110-115. ZHANG HONGSHUN,UUNLIN,ZHAN JIANGSHU. Signal-subspace-based esprit-like algorithm for coherent DOA estimation[J]. Journal on Communication,2010,31(7):110-115.(in Chinese) [11]CADZOW J A,KIMS,SHIUE D C. General directionof- arrival estimation:a signal subspace approach[J]. IEEE Transactions on Aerospace and Electronic Sstems,1989,25(1):31-46. An DOA Estimation Algorithhmm of Coherent Signals Based on Conviance Matri Abstrraacctt:: For the direction of arrival (DOA) of coherent signals, a new algorithm based on covariance matrireconstruction named TSV-ESPRIT was proposed. The signal eigenvectors including the direction information of all sources was used to construct the Toeplitz covariance matri. This construction method is without reducing the arraaperture and increase esti⁃mation resolution and stabilit. The estimation of signal parameter via rotational invariance techniques (ESPRIT) instead of multiple signal classification (MUSIC) was used to avoid the peek searching and reduce the computational compleit. Sim⁃ulation results and analsis proved the validitand effectiveness of the algorithm. 作者简介:刘晓娣(1982-),女,讲师,硕士。 收稿日期:2014-10-09; DOI:10.7682/j.issn.1673-1522.2015.02.005 文章编号:1673-1522(2015)02-0120-05 文献标志码:A 中图分类号:TN929.53 修回日期:2015-01-20
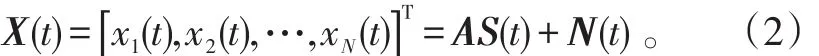

2 基于协方差矩阵重构的TSVD-ESPRIT算法


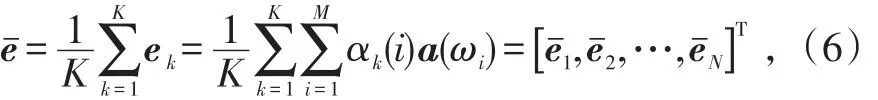


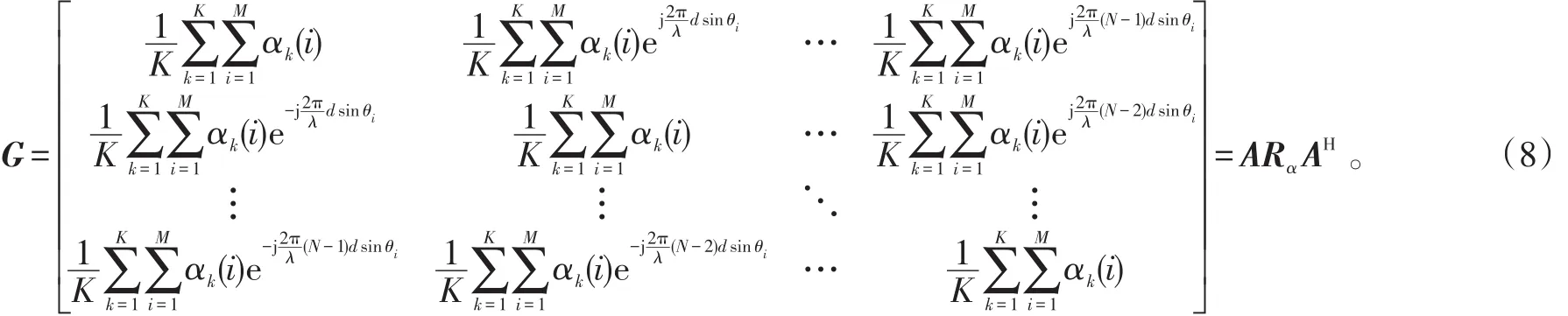


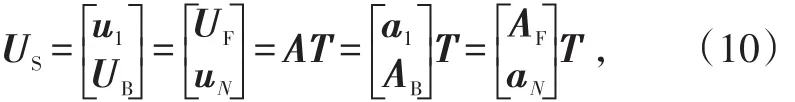



3 数值仿真



4 结论

