基于STFRFT的LFM引信抗欺骗干扰方法
粘朋雷,李国林,李 飞(海军航空工程学院.研究生管理大队;.七系,山东烟台264001)
基于STFRFT的LFM引信抗欺骗干扰方法
粘朋雷a,李国林b,李飞a
(海军航空工程学院a.研究生管理大队;b.七系,山东烟台264001)
摘要:针对线性调频脉冲压缩引信易受转发式假目标欺骗干扰问题,提出了基于短时分数阶傅立叶变换(ST⁃FRFT)的抗欺骗干扰方法。首先,通过分数阶傅立叶变换将回波信号与欺骗干扰各分量信号进行分离;再利用相同调频率的LFM信号经短时分数阶傅立叶变换后最大幅值与窗函数宽度成线性关系,而不同调频率的最大幅值不随窗函数宽度变化的特点,有效分辨假目标欺骗干扰,正确检测目标回波信号;最后,通过仿真证明了方法的正确性,并验证所提方法具有良好的抗欺骗干扰效果。
关键词:线性调频;欺骗干扰;短时分数阶傅立叶变换;干扰抑制
线性调频脉冲信号以其高探测距离和距离分辨率,越来越多地被应用于高分辨雷达和引信设备中。随着高速集成数字器件应用于先进的干扰设备,特别是基于DRFM技术的假目标欺骗干扰,通过对引信信号进行截获、采样、存储、转发,产生与引信信号高度相关并能获得引信很高的处理增益的干扰形式[1],对引信产生有效的欺骗干扰[2-4]。
由于LFM信号为宽带信号,引信回波信号与干扰信号间存在很强的耦合性,出现了许多利用时频分析方法的干扰抑制技术。文献[5]提出了一种应用于雷达的灵巧干扰剔除技术,但是对于引信这种体积小的装备,不适合安装体积过大带发射接收天线的剔除装置。文献[6-7]提出的方法是分别从时域和频域分离目标回波信号和单个假目标干扰,但无法对多假目标干扰进行有效的抑制。对于斜率抖动的LFM引信[8],由于其调频率是不断变化的,因而对于转发式欺骗干扰信号与引信回波信号是正交的,但是当干扰信号与回波信号调频率很接近时,干扰强度很小就可以超出引信的抗干扰门限。文献[10-12]中使用的短时傅里叶变换在处理单分量LFM信号时有一定的作用,但是当处理多分量LFM信号时也会产生交叉项。分数阶傅立叶变换[13-15]使用单一变量来表示时频信息,没有交叉项的困扰,但是在信号调频率很接近时,需要很小的搜索步长,这将使得运算量成指数倍增加。
本文从分析FRFT域旋转角度与LFM信号调频率是否匹配产生的最大幅值与信号宽度的关系入手,提出了基于STFRFT的引信抗欺骗干扰方法。首先,利用FRFT将引信接收信号中各信号分量进行分离;然后,对各分量进行STFRFT处理,与FRFT结果进行比较,根据2次脉冲压缩各个压缩峰值的幅值变化,确定哪一个分信号为目标回波信号,从而有效分辨假目标欺骗干扰,正确检测目标回波信号。
1 欺骗干扰对SVLFM引信的影响

斜率抖动线性调频引信第m个脉冲周期发射的信号下变频后可表示为式中为LFM信号的调频率;B为带宽;ξm为信号调频率的抖动参数,是由引信产生的随机序列。
为保证不同脉冲周期信号保持相同的频率带宽,第m个脉冲信号的脉宽随ξm变化而变化。
干扰设备对引信信号进行截获、采样、存储、转发,产生引信信号高度相关的欺骗干扰,因而引信需要不断地改变调频率。为保证引信的探测距离和距离分辨力,斜率抖动参数ξm不可能在无限空间内随机取值,而应选择为原信号调频率的某一比例。因此,干扰信号的调频率可能与某脉冲周期的调频率接近。
图1为LFM信号斜率抖动参数ξm变化不同比例时的脉冲压缩结果。
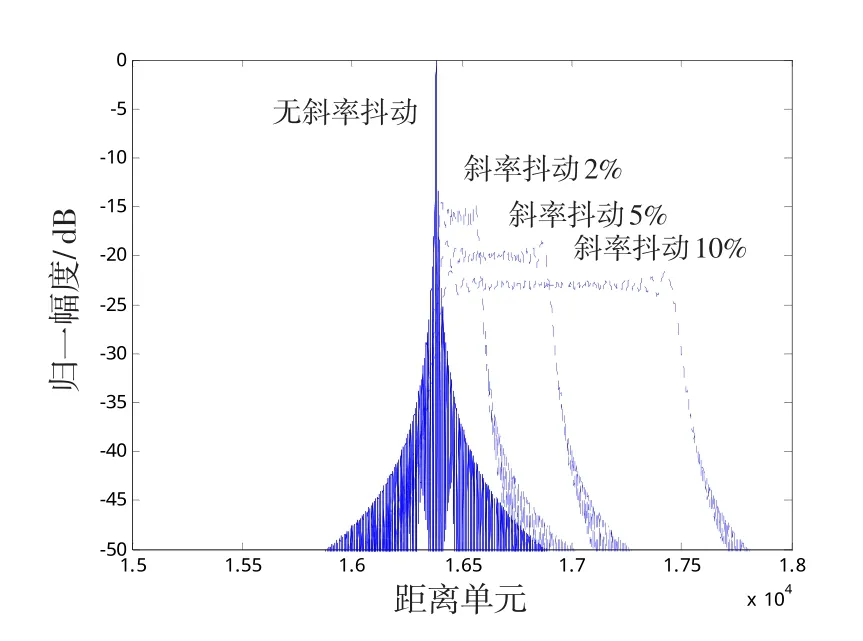
图1 不同信号脉压结果图Fig.1 Pulse compression of different signal
图1中,ξm的变化使得干扰信号与引信发射信号的相关性降低,导致脉压后主瓣变宽,幅度降低。但是当斜率抖动比较低,干信比ISR比较高时,欺骗干扰信号仍能输出较高的脉压结果,达到干扰的目的,因而必须采取相应的抗干扰措施。
2 基于STFRFT的抗欺骗干扰
2.1基于FRFT的信号分离
FRFT是一种广义的Fourier变换,傅立叶变换是一种线性算子,若将其看作从时间轴逆时针旋转π 2到频率轴,分数阶傅立叶变换算子就是可旋转任意角度α的算子。因此,分数阶傅立叶域上同时包含了时域和频域信息,对LFM信号有很好的能量聚集特性。
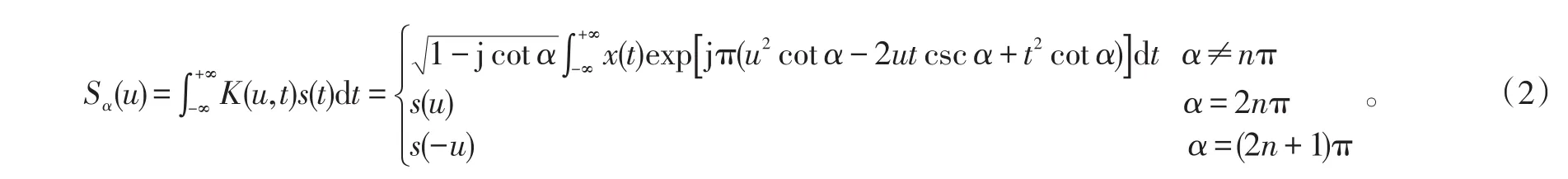
信号s(t)的分数阶傅立叶变换定义为:式(2)中:α为FRFT域旋转角度;n是整数。
对于调频率为μ的LFM信号,当在分数阶傅立叶域旋转角度α=-arccotμ时,信号会变成冲击函数,不同的调频率对应不同的旋转角度。当调频率与旋转角度不匹配时,则不会出现冲击函数,通过合适宽度的带通滤波器,经过分数阶傅立叶反变换可得到对应的LFM信号分量。当信号中含有多个调频率的LFM分量时,可根据能量的大小,逐步获得各个信号分量。对于引信接收信号,可通过此方法在FRFT域获得好的滤波和干扰分离效果,获得回波信号分量和欺骗干扰信号中各个干扰分量,完成信号的分离。
2.2 STFRFT原理分析
虽然不同调频率在其对应的旋转角度形成能量的积累,但当不同LFM信号的调频率很接近时,仍会在不匹配的旋转角度产生能量的积累,只是积累效果不是最佳,这种情况下只能将各分量进行分离,而无法区分回波信号和欺骗干扰信号。
假设某个脉冲周期,LFM信号的斜率抖动参数为0,则其信号为:式中,A为信号幅值。不失一般性,可令φ=0。
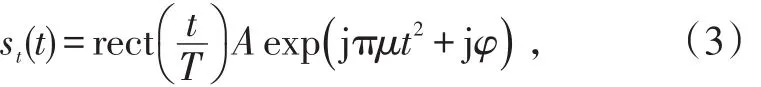
信号st(t)的分数阶傅立叶变换可表示为

根据FRFT的能量聚集性质,LFM信号在FRFT域能量最佳聚集的旋转角度为αm=-arccotμ,且其范围限定为( )

由式(4)知,Sαm( ) u的模最大值出现在u=0处,且最大值为
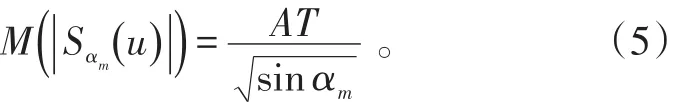
在信号st(t)的幅度A一定,调频率μ确定的情况下,FRFT的最佳旋转角度αm也是确定的与进行FRFT的脉冲信号宽度T成线性关系;当对信号st(t)进行短时分数阶傅立叶变换,即对需处理的信号进行加窗处理,窗函数为,式(4)变为:随着窗函数的宽度Tw而成比例的变化。

若信号的调频率为μ+ξm,其中抖动参数ξm≠0,对此信号进行旋转角度为αm=-arccotμ的短时分数阶傅立叶变换得:

当ξm≠0时,Swαm(u )为菲涅尔积分,忽略复函数其包络为式中:C(∙ )、S(∙ )为菲涅尔积分函数;
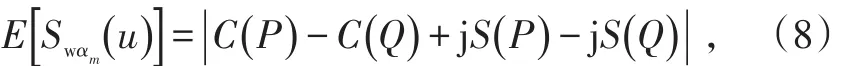

菲涅尔积分无法得到精确值,通过计算机仿真得当ξm≠0时,经过分数阶傅立叶变换后信号幅值最大值保持不变,与进行脉冲信号宽度Tm无关,只是输出主瓣宽度随着Tm变化,与其成线性关系。对信号进行窗函数为的短时分数阶傅立叶变换,所得对比结果如图2所示。

图2 加窗前后FRFT图Fig.2 Different signal STFRFT
图2 a)、b)为ξm=0时STFRFT图,加窗后幅值最大值变为加窗前的1;图2 c)、d)为ξ≠0时STFRFT
2m图,加窗前后幅值最大值不变;图2 e)、f)为图2 c)、d)的局部放大图,加窗后幅值不变,但主瓣宽度变为加窗前的1。
2
2.3干扰抑制方法实现
对于SVLFM引信,只有目标回波信号才与发射信号的调频率参数相同,其他脉冲周期的信号调频率与其不同。因此,引信首先利用分数阶傅立叶变换对接收信号进行信号分离,而回波信号的调频率是已知的,分数阶域的旋转角度即可固定。根据2.2节的分析,可通过对各信号分量的分数阶傅立叶变换与短时分数阶傅立叶变换作比较,如果幅值最大值不变,则该信号分量为干扰信号所得;如果幅值发生显著变化,则该信号分量为目标信号所得。SVLFM引信抗欺骗干扰方法原理如图3所示。

图3 干扰抑制原理Fig.3 Interference suppression principle
为了使目标回波信号在STFRFT前后所得幅值最大值有显著变化,在此取加窗系数:式(9)中:宽度为引信发射信号脉冲宽度最小值;τi为各信号分量的延时。

则信号周期最小的信号经STFRFT信号幅度最大值也将变为加窗前的1。干扰信号为了达到欺骗干
2扰的目的,不断改变干扰信号的延时,通过信号分离可确定各信号分量的延时τi,当接收信号压缩含有多个尖峰时,须分别将短时分数阶傅立叶变换与分数阶傅立叶变换进行比较,确定目标回波信号。
3 仿真实验及结果分析
仿真取引信回波信号的脉冲宽度为1 μs,频率带宽为200 MHz,则调频率为2×1014Hz,干扰信号取含有2分量LFM信号,调频率与回波信号调频率相差分别为5%和10%,信干比SIR=-10dB,信噪比SNR= -5dB,采样率为1 GHz。对含有2分量干扰的引信接收信号进行分数阶傅立叶变换所得结果见图4。
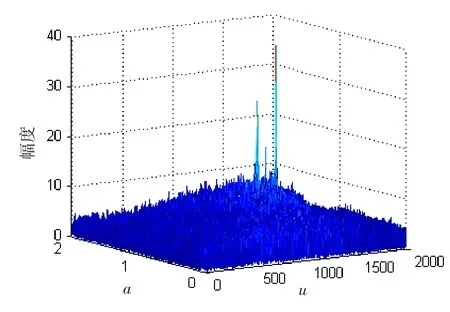
图4 分数阶傅立叶变换结果Fig.4 Rosult of signal FRFT
通过分数阶傅立叶变换,可将引信接收信号各LFM分量按照功率由大到小依次进行分离,得到目标回波信号与欺骗干扰各分量信号如图5所示。通过对3个信号分别进行分数阶傅里叶变换和短时分数阶傅里叶变换,对比结果如图6所示。

图5 分离信号波形Fig.5 Separated signal
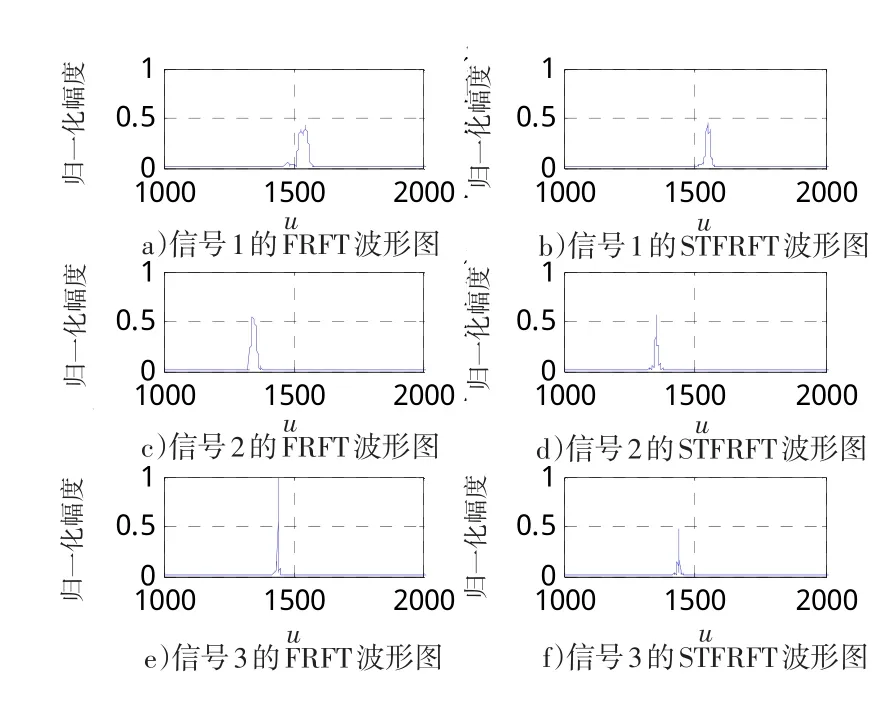
图6 信号FRFT与STFRFT对比Fig.6 Contract of signal FRFT and STFRFT
从图6中可看出,图6 a)、b)为图5 a)信号经FRFT 和STFRFT对比图,信号幅值基本不变,而宽度变窄。图6 c)、d)为图5 b)信号经FRFT和STFRFT对比图,信号幅度仍然未发生变化。但是图6 e)、f)的幅值对比变化约1。由此可以判断,图5 c)对应的信号分量
2为目标回波信号。
5 结论
斜率抖动LFM引信对基于DRFM技术的欺骗干扰具有一定的抗干扰性,但是当干扰信号与目标回波信号调频率抖动较小时,在一定的干信比时,干扰信号仍能达到欺骗目的。针对这一问题,本文通过分析信号经分数阶傅里叶变换后幅度最大值与信号宽度的关系,提出了基于短时分数阶傅里叶变换的抗欺骗干扰方法,仿真验证了该方法能够有效分辨假目标欺骗干扰,正确检测目标回波信号。
参考文献:
[1]GRECO M,GINI F,FARINA A. Radar detection and classification of jamming signals belonging to a cone class[J]. IEEE Transactions on Signal Processing,2008,56(5):1984-1993.
[2]张煜,杨绍全.对线性调频雷达的卷积干扰技术[J].电子与信息学报,2007,29(6):1408-1411. ZHANGU,ANG SHAOQUAN. Concolution jamming technique countering LFM radar[J]. Journal of Electronics and Information Technolog,2007,29(6):1408-1411.(in Chinese)
[3]葛青林,王莹莹,李静.一种产生雷达多假目标的卷积调制法[J].现代防御技术,2012,40(1):137-139. GE QINGLIN,WANGINGING,LI JING. A kind of convolution modulation method that generate radar multifalse target[J]. Modern Defense Technolog,2012,40 (1):137-139.(in Chinese)
[4]胡敏,李国林,张颖.数字多时延灵巧干扰信号研究[J].电讯技术,2010,50(6):21-27. HU MIN,LI GUOLIN,ZHANGING. Studon digital multidelasmart jamming signal[J]. Telecommunication Engineering,2010,50(6):21-27.(in Chinese)
[5]王存卫,王永良,李荣峰.一种有效的灵巧干扰剔除技术[J].空军雷达学院学报,2010,24(4):244-246. WANG CUNWEI,WANGONGLIANG,LI RONGFENG.An effective technique for smart jamming elimina-tion[J]. Journal of Air Force Radar Academ,2010,24 (4):244-246.(in Chinese)
[6]张淑宁,赵惠昌,熊刚.基于延时变化量估计的伪码引信抗欺骗式干扰方法[J].宇航学报,2008,29(1):326-330. ZHANG SHUNING,ZHAO HUICHANG,IONG GANG. The method of frandulent interference ecision based on time deladifference estimation for PN fuze[J]. Journal of Astronautics,2008,29(1):326-330.(in Chinese)
[7]卢刚,唐斌,罗双才. LFM雷达中DRFM假目标自适应对消方法[J].系统工程与电子技术,2011,33(8):1760-1764. LU GANG,TANG BIN,LUO SHUANGCAI. Adaptive cancellation of DRFM false targets for LFM radar[J]. Sstems Engineering and Electronics,2011,33(8):1760-1764.(in Chinese)
[8]MEHRDAD SOUMEKH. SAR-ECCM using phase-perturbed LFM chirp signals and DRFM repeat jammer penalization[J]. IEEE Transactions on Aerospace and Electronic Sstems,2006,42(1):191-204.(in Chinese)
[9]LIANG ZHAO,AMIN M G,LINDSEA R. Subspace projection techniques for anti-FM jamming GPS receivers [C]//Proceedings of the Tenth IEEE Workshop on Statistical Signal and ArraProcessing. Pocono Manor,PA,2000:529-533.
[11]温景阳,张焕宇,王越.线性调频脉冲压缩雷达信号参数估计方法[J].北京理工大学学报,2012,32(7):746-750. WEN JINGANG,ZHANG HUANU,WANGUE. Parameters estimation algorithm of LFM pulse compression radar signal[J]. Transaction of Beijing Institute of Technolog,2012,32(7):746-750.(in Chinese)
[12]ZHAO ZHAO,SHIIANGQUAN. FM interference suppression for PRC-CW radar based on adaptive STFT and time-varing filtering[J]. Journal of Sstems Engineering and Electronics,2010,21(2):219-223.
[14]TANG PENGFEI,UAN BIN,BAO QINGLONG. Design and simulation of digital channelized receivers in fractional Fourier domain[J]. Journal of Sstems Engineering and Electronics,2013,24(1):36-43.
[15]敦鹏,竺小松,薛万成.基于RFRFT技术的LFM信号去相关分离方法[J].电子信息对抗技术,2013,28(1):17-20. DUN PENG,ZHUIAOSONG,UE WANCHENG. Decorrelation separation method of LFM signal based on RFRFT[J]. Electronic Information Warfare Technolog,2013,28(1):17-20.(in Chinese)
Deception Jamming Suppression Methoodd of LFM Fuze Based on STFRFT
NIAN Peng-leia, LI Guo-linb, LI Feia
(Naval Aeronautical and Astronautical Universita. Graduate Students’Brigade; b. No.7 Department,antai Shandong 264001, China)
Abstrraacctt:: Aiming at the deception jamming for LFM fuze, a new method based on STFRFT(short time fractional fourier transform) was proposed to suppress the interference. The frequencmodulation ratio of SVLFM(slope varing linear fre⁃quencmodulation) fuze changed at random in everpulse period, so the target echo and the deceptive signal could be sep⁃arated bFRFT. Because of the characteristic that the maamplitude of STFRFT was linear with the windowing width for the same LFM signal, but the maamplitude was not change with the windowing width if two frequencmodulation ratio was different, then the target echo could be distinguished from the false target signal effectivelunder low SJR. Simulation results showed that the principle was right and the method had good abilitto suppress deceptive interference.
作者简介:粘朋雷(1986-),男,博士生。
基金项目:国家自然科学基金资助项目(61102165)
收稿日期:2014-11-30;
DOI:10.7682/j.issn.1673-1522.2015.02.003
文章编号:1673-1522(2015)02-0111-05
文献标志码:A
中图分类号:TN973
修回日期:2015-01-09

