用“图形语言”思考问题——也谈“几何直观”在小学数学教学中的运用

□江苏省常熟市辛庄中心小学　贾兰

用“图形语言”思考问题
——也谈“几何直观”在小学数学教学中的运用

□江苏省常熟市辛庄中心小学贾兰

义务教育数学课程标准（2011版）提出了“几何直观”这一核心概念，认为：“几何直观主要是指利用图形描述和分析问题。借助几何直观可以把复杂的数学问题变得简明、形象，有助于探索解决问题的思路，预测结果。”在小学数学教学中，教师要适时向学生渗透“几何直观”思想，提高其思维能力和解决问题的能力。

图形转化几何直观提高能力

我国数学家徐利治教授认为：“几何直观是借助于见到的或想到的几何图形的形象关系产生对数量关系的直接感知。”因此，在小学数学教学中，教师要利用“图形”的直观性，引导学生用画图的策略将直观图与数学语言、符号语言进行合情转换，并通过数形结合感悟数与形、形与数之间的转化，适时向学生渗透“几何直观”的思想，提高学生的思维能力和解决问题的能力。

一、以“图”表征，揭示运算概念的本质

在教学乘法分配律之后，教师总会发现学生中存在着大量的运算错误，主要形式是“（a+b）×c”演算成“a×c+b”。究其原因是学生对乘法分配律概念的理解只停留在识记和模仿层面，他们只经历了从“数”到“数”、从“算”到“算”的建构过程，对乘法分配律引入的表征感悟不深。那么，以什么来表征乘法分配律才能让学生真正理解乘法分配律的概念呢？笔者认为借助“几何直观”中数与形的对应关系进行教学，无疑是揭示运算概念本质的有效途径之一。

例如，在教学时，教师可以设计如下情境题：新安小学原来有一个长方形操场，长100米，宽50米。扩建后，长增加20米，宽不变。扩建后的操场面积是多少平方米？

师：你能先画出图形，再用两种方法求出现在这个操场的面积吗？

学生汇报，画出图形：

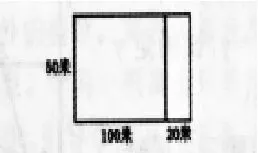
方法一：（100+20）×50=6000（平方米）

方法二：100×50+20×50=6000（平方米）

师：由此可见，（100+20）×50和100×50+20×50是相等的，我们可以写成（100+20）×50=100×50+20×50。那左边的式子乘了一个50，右边的式子乘了两个50，左右为什么还会相等呢？

生：（100+20）×50表示先求现在长方形操场的长，再用长×宽求出现在长方形操场的面积；100×50+20×50表示先求原来长方形操场的面积，再求增加出来的那部分面积，最后把两部分面积合起来就是现在长方形操场的面积。所以（100+20）×50和100×50+20×50的结果是相等的。

师：（100+20）×50能不能写成100×50+20呢？

生：不能。因为（100+20）×50算出的是现在长方形操场的面积，而100×50+20求的是原来长方形面积与长增加出来的一部分长度的和，并不是现在长方形操场的面积。

师：你能把自己的意思画出来吗？

学生板书：

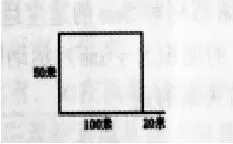
在这一教学中，学生原本对乘法分配律中数的变化并不在意，他们很清楚用两种方法求出的操场面积肯定相等。但通过画图，他们不得不把注意力集中在数字50上，对每一步运算代表的直观意义有了清晰的解读。在例证（100+20）×50不能写成100×50+20时，教师利用从“数”到“形”的直观图形加以表征，使学生对乘法分配律的基本模型有了较为深刻的理解，无形中减少了类似“（a+b）×c=a×c+b”这样的错误。

二、用“图”描述，创新分析问题的方法

心理学研究表明，小学生的思维水平正处于具体运算阶段向形式运算阶段过渡的时期，他们的学习和思考离不开具体事物的支持。因此，在教学时，教师要鼓励学生用直观形象的图形、符号把问题表述出来，把思考的过程描述出来，把看不见的抽象思维显现出来，真正将抽象的数学语言与直观的图形语言结合起来，充分发挥出“几何直观”的优势。

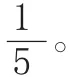
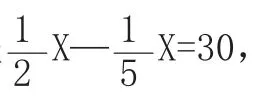
针对此种现象，教师提问：你们能用线段图描述出题目的意思吗？

结合学生回答，板书出线段图：

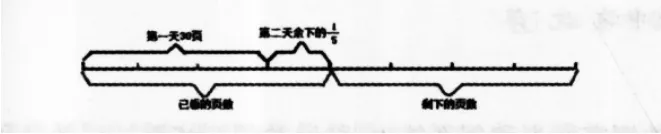
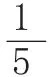
线段图作为一种基于数形结合的数学思想，能将自然语言转译为图形语言，为数学思维活动提供直观模型，变抽象为具体，化繁琐为简单。在上述教学中，教师引导学生画出线段图，将题中蕴含的抽象的数量关系以形象、直观的方式表达出来，不仅创新了学生分析数量关系的方法，开拓了学生的思维，还培养了学生的“几何直观”意识。

三、让“图”说话，明晰概念知识的内涵

在数学教学中加强数学概念几何意义的阐释，有利于学生形成概念表象，促进其对数学知识的理解和记忆，积累表象构建的经验。例如，长度、面积、体积这三个量在概念内涵的语言表述上是有差异的。“长度”是一维的概念，表示物体或线段长短的程度；“面积”是二维的概念，表示物体表面或平面图形的大小；“体积”是三维的概念，表示物体所占空间的大小。但若仅用这样的语言去描述其不同的本质，学生往往不能正确地理解。因此，为了梳理和沟通这些概念之间的区别与联系，帮助学生对这些概念形成既清晰又丰富的认识，教师结合以下图形进行了教学。

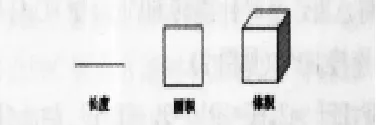
师：谁能结合图形说说长度、面积、体积这三个量有什么不同？

生：长度表示线段的长短；面积表示面的大小；体积表示占的空间的大小。

师：那度量这三个量所用的单位分别是什么？

生：长度单位一般是厘米、分米、米；面积单位一般是平方厘米、平方分米、平方米；体积单位一般是立方厘米、立方分米、立方米。

师：这些相邻单位间的进率分别是多少？

生（思索了一会儿）：相邻的长度单位间进率一般是10；相邻的面积单位间进率一般是100；相邻的体积单位间进率一般是1000。

师：你有什么好方法可以记住这些单位间的进率吗？

教师引导学生观察上图，并适时增添为：

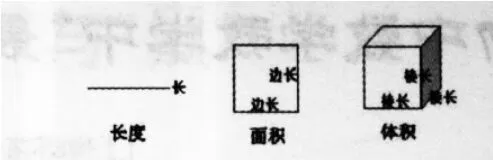
让学生观察、比较，归纳出结论：“长度”是一条线段“长”，所以相邻单位间进率为10；“面积”是一个面，由边长×边长得出，即10×10=100，所以相邻单位间进率为100；“体积”是一个立体图形，由棱长×棱长×棱长得出，即10×10× 10=1000，所以相邻单位间进率为1000。

四、画“图”探究，优化解决问题的途径

数学家华罗庚先生说：形使数更直观，数使形更入微。如在教学“用替换的策略解决实际问题”时，笔者出示例题：小明把720毫升果汁倒入6个小杯和1个大杯，正好都可以倒满。大杯的容量是小杯的3倍。一个大杯的容量是多少毫升？一个小杯的容量是多少毫升？

教师让学生独立思考后，引导学生根据自己对题意的理解画出简单的示意图：

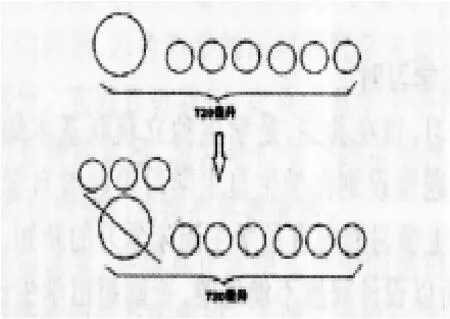
师：从图中可以看出，我们把什么替换成了什么？总量有没有变？

生：把1个大杯替换成了3个小杯。总量没有变。

师：观察上、下图，总量没有变，那什么变化了？

生：原来720毫升的果汁是装在1个大杯和6个小杯中的；通过替换，720毫升的果汁装在了9个小杯中。

师：这样一变化，由两种不同的杯子换成了一种相同的杯子，这个问题就能顺利解决了。现在大家能用算式求出一个小杯的容量和一个大杯的容量分别是多少毫升吗？

生：能。

数形结合是将抽象的数学语言与直观的图形语言有机地结合起来，实现数量关系与图形性质的相互转化，充分展现问题本质的数学方法。在上述教学中，学生通过画一画、换一换，真切地感受到具体的替换过程，接着又借助符号、图形的替换实现了从具体到半抽象的过程，最后是通过抽象的算式使这个替换策略数学化，真正做好了图形与数学语言之间的变换。

总之，“几何直观”作为一种思维方式，在整个数学学习过程中发挥着重要作用。在教学中，教师要充分引导学生利用“几何直观”来进行数学思考和想象，提高思维的灵活性和深刻性，激发学生的创造意识，进而提高学生的学习能力。

［1］中华人民共和国教育部［M］.义务教育数学课程标准（2011版）.北京师范大学出版社，2012.

［2］曹培英.跨越断层，走出误区：“数学课程标准”核心词的实践解读之四——几何直观（上）［J］.小学数学教师，2013（6）.