初中数学教学中“最近发展区”的确定及其利用
□江苏省苏州市吴中区迎春中学 沈萍
初中数学教学中“最近发展区”的确定及其利用
□江苏省苏州市吴中区迎春中学沈萍
“最近发展区”理论倡导教学时挖掘学生的潜力,开发学生的探究能力和创新能力;鼓励教师要注重过程教学和启发式引导,准确把握学生的“最近发展区”,并以此为施教的切入点,最大限度地提高教学效益。
切入点初中数学最近发展区
在实际数学教学中,应该在学生已有经验水平的基础上,找到最利于教育发展的“最近发展区”,努力创造条件,为学生提供自主探索、充分思考的空间,去理解知识的形成和发展过程,进行知识再造,从而能利用已有的知识储备,解决新的数学问题,同时也培养了学生的能力,激发了学生学习知识的信心和勇气。那么,在数学教学中如何确定和利用最近发展区呢?
一、自主学习时
自主学习,贵在独立,是学生独立获取基本知识的重要一环。而问题预设则在学生自主学习中起着自学导航的作用。由于自主学习的内容是学生尚未学习的新知,而且没有老师带领,所以设计问题不能过难,否则超出学生已有水平,不利于其自主学习。在问题预设时,要确定最有利于学生自主学习的最近发展区,利用最近发展区使学生有效自主学习。如我在教学“分式方程”第二课时前,让学生自主学习。首先确定学生的最近发展区为“分式方程产生增根”这个难点。为了突破这个难点,预设以下问题:
1.上节课学习解分式方程的步骤是什么?请用这个步骤解这个分式方程:

2.在检验时发现与上节课不一样的地方是什么?
3.你觉得解出来的解x=2是你去分母后得到的整式方程的解吗?
4.你觉得解出来的解x=2是原分式方程的解吗?
5.什么是增根?
6.你觉得增根产生的原因是什么?
针对“分式方程增根的理解”这个难点,在学生自主学习时,我设计的预设问题正是分解难点,在关键处设问;这样学生在自主学习中就能自行感悟到解分式方程时产生增根的原因了。
二、新知学习时
数学知识是一环套一环的,每个知识点都有承先启后之效。所以在学习新知时,我们可以找到这个知识点前面的知识储备,给学生提供思考空间,让学生利用先前的学习经验,“跳一跳”来学习新知。如我在教学“同底数的幂的除法”时,首先考虑的是学生已有的知识水平和最近发展区的确定。大部分学生已掌握同底数的幂的乘法,从已有知识“同底数的幂的乘法”到“同底数的幂的除法法则的引入”,这之间的差距也就是学生需要突破的最近发展区。于是我创设了如下问题情境:

首先让学生用已有的知识储备“同底数的幂的乘法”完成4个乘法式子的填空,然后将以上四个乘法式子表示成除法算式,接着引导学生分析除法算式的特点和规律,并由学生总结同底数的幂的除法法则,从而达到学生用旧知识“跳一跳”来学新知识的目的。
三、交流讨论时
比如,课上要解决这样一个问题:如图1,点P是等边三角形ABC内的一点,∠BPC=150°,PB=2,PC=3,求PA的长。
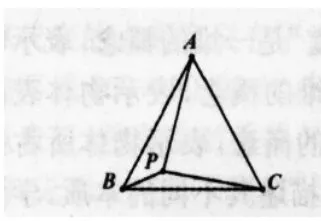
图1

图2
解:∵△ABC是等边三角形,
∴BC=BA,∠ABC=60°.
∴将△BPC逆时针旋转60°,使BC与BA重合,得到△BAP′,连接PP′(见图2).
∴BP=BP′=2,PC=AP′=3,∠B P′A=∠BPC=150°,∠PBP′=60°.
∴△BPP′为等边三角形.
∴∠BP′P=60°,PP′=2.
∴∠AP′P=∠B P′A-∠BP′P=150°-60°=90°.
首先笔者采用分组讨论的形式,给学生一定的时间思考,然后了解学生的现有水平,来确定学生的最近发展区。我发现利用“旋转”添加辅助线是学生的困难所在,超出了他们的已有水平,他们不易想到。因此,为了接近学生的最近发展区,使学生想到利用“旋转”添加辅助线,解决该问题,可以先让学生先完成热身练习:如图2,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10。若将△PBC绕点B逆时针旋转后,得到△P′AB,则点P与点P'之间距离为多少?∠APB的度数是多少?
此练习与课上要解决的例题类似,却并不完全一样。此练习中“若将△PBC绕点B逆时针旋转后,得到△P′AB”即已知旋转后的三角形,为例题中“旋转”辅助线的添加做出了铺垫;设置的两个问题也为解决例题搭建了阶梯,从而可以调动学生的积极性,使学生的思维水平得到进一步提高。
四、练习巩固时
思维链比较长的一些练习题,学生往往难以理解,不易上手,因为这超出了他们的原有水平。因此,我们可以确定并利用学生的最近发展区,做好铺垫,设置好学生思维的阶梯,使学生熟练并灵活运用新知。如例题:已知二次函数的图象经过A(-3,0),B(1,0),C(0,-3),求这个二次函数解析式。为了使学生熟练掌握,我设置以下3个变式练习——
变式1:已知二次函数图象经过一次函数y=-x-3图象与x轴、y轴的交点A、C,且经过B(1,0),求这个二次函数的解析式。
变式2:已知抛物线经过B(1,0),C(0,-3),且对称轴为直线x=-1,求这条抛物线的解析式。
变式3:已知二次函数图象经过直线y=-3x+3与x轴、y轴的交点,对称轴为直线x=-1。设该函数图象与x轴交点为A、B(点A在点B左边),与y轴交点为C,顶点为D,求二次函数解析式。
对于变式3,很明显思维链较长。刚讲完例题后,如果直接让学生完成思维链较长的练习,部分学生会很难上手,超出了他们的已有水平。如何将较长的思维链进行分解也就是突破最近发展区的关键。因此,我将变式3进行分解,设计了变式1和变式2,这两个变式思维链较短,学生易上手,从而为变式3做好铺垫,利用最近发展区,使学生的思维水平得到进一步提高。
数学教育家余文森先生指出:“只有针对最近发展区的教学,才能促进学生的发展。发展的过程就是不断把最近发展区转化为现有发展区的过程。”在数学教学中,不仅要使学生在思维能力、情感态度与价值观等方面得到进步与发展,而且要使数学教育面向全体学生,实现“人人学有价值的数学,不同的人在数学上都有不同的发展”。

